| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A151 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322356 | |
| Published online | 29 January 2014 | |
Understanding the dynamical structure of pulsating stars
HARPS spectroscopy of the δ Scuti stars ρ Puppis and DX Ceti ⋆
1 Laboratoire Lagrange, UMR7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, Nice, France
e-mail: [email protected]
2 INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
3 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
4 Université de Toulouse, UPS-OMP, IRAP, 65000 Tarbes, France
5 CNRS, IRAP, 57 avenue d’Azereix, BP 826, 65008 Tarbes, France
Received: 24 July 2013
Accepted: 5 December 2013
Context. High-resolution spectroscopy is a powerful tool to study the dynamical structure of a pulsating star’s atmosphere.
Aims. We aim at comparing the line asymmetry and velocity of the two δ Sct stars ρ Pup and DX Cet with previous spectroscopic data obtained on classical Cepheids and β Cep stars.
Methods. We obtained, analysed and discuss HARPS high-resolution spectra of ρ Pup and DX Cet. We derived the same physical quantities as used in previous studies, which are the first-moment radial velocities and the bi-Gaussian spectral line asymmetries.
Results. The identification of f = 7.098 d-1 as a fundamental radial mode and the very accurate Hipparcos parallax promote ρ Pup as the best standard candle to test the period–luminosity relations of δ Sct stars. The action of small-amplitude nonradial modes can be seen as well-defined cycle-to-cycle variations in the radial velocity measurements of ρ Pup. Using the spectral-line asymmetry method, we also found the centre-of-mass velocities of ρ Pup and DX Cet, Vγ = 47.49 ± 0.07 km s-1 and Vγ = 25.75 ± 0.06 km s-1, respectively. By comparing our results with previous HARPS observations of classical Cepheids and β Cep stars, we confirm the linear relation between the atmospheric velocity gradient and the amplitude of the radial velocity curve, but only for amplitudes larger than 22.5 km s-1. For lower values of the velocity amplitude (i.e., <22.5 km s-1), our data on ρ Pup seem to indicate that the velocity gradient is null, but this result needs to be confirmed with additional data. We derived the Baade-Wesselink projection factor p = 1.36 ± 0.02 for ρ Pup and p = 1.39 ± 0.02 for DX Cet. We successfully extended the period–projection factor relation from classical Cepheids to δ Scuti stars.
Key words: stars: oscillations / stars: atmospheres / line: profiles / stars: individual: rho Puppis / stars: individual: DX Ceti / stars: distances
© ESO, 2014
1. Introduction
The variability of ρ Pup ≡ HD 67523 ≡ HR 3185, one of the brightest (V = 2.88) δ Sct stars, was first reported by Cousins (1951) and then clearly demonstrated by Eggen (1956) and Ponsen (1963). An accurate value of the pulsational period (P = 0.14088143 d) was determined from photometric data spanning fifty-two years (Moon & van Antwerpen 2009). Atmospheric parameters (effective temperature, surface gravity, and metallicity) were determined from ELODIE spectra by using the MILES library interpolator (Prugniel et al. 2011): Teff = 6810 ± 121 K, log g = 3.59 ± 0.14, and [Fe/H] = + 0.60 ± 0.05. The [Fe/H] value confirms that ρ Pup is a member of the δ Del subgroup, that is, late-A and early-F subgiants showing spectra with enhanced metal-lines (especially the Fe I, Y II, Fe II and Zr II ones) and normal H and Ca II lines (Kurtz 1976,and references therein). ρ Pup is a well-known case where the determinations of the atmospheric parameters by means of Strömgren photometry (b − y = 0.259, m1 = 0.215, c1 = 0.731, β = 2.715) disagree in function of the photometric indices used in the calibrations. This could be ascribed to its particular metallic content. Indeed, the spectroscopic values agree excellently with those obtained from b − y and c1 indices, that is, 6850 K and log g = 3.5 (Breger 1974; Kurtz 1976). Pioneering IUE spectra show emission features in the Mg II lines throughout the pulsation cycle (Fracassini et al. 1983). Later, detailed spectroscopic investigations of the pulsation properties were performed by Mathias et al. (1997) and Dall & Frandsen (2002). Very recently, the results of a dedicated spectroscopic multisite campaign excluded solar-like oscillations with an amplitude per radial mode larger than 0.5 m s-1 (Antoci et al. 2013).
DX Cet ≡ HD 16189 is a bright high-amplitude δ Sct (HADS) star with a period P = 0.103939529 d and full amplitude of 0.20 mag in V light (Kiss et al. 1999). Stellar parameters were obtained from uvbyβ photometry (Kiss et al. 1999; Stetson 1991): Teff = 7250 ± 200 K, log g = 3.6 ± 0.2 dex.
Comparing the spectroscopic analysis of these two δ Scuti stars (ρ Pup and DX Cet) with previous results obtained on classical Cepheids and β Cep stars is extremely interesting for various reasons. First, for a given pulsating star, and also when comparing one star to the other, the spectral lines asymmetry show a systematic difference in average (over one pulsation cycle) that is positive or negative, depending on the spectral line considered. This effect is related to the dynamical structure of the star’s atmosphere and has been investigated in the case of classical Cepheids by means of the k-term (Nardetto et al. 2008, 2009). Since the physical origin of this phenomenon is currently not understood, the comparison of the results obtained for several types of pulsating stars is particularly helpful. Second, Nardetto et al. (2013) found a linear relation between the atmospheric velocity gradient and the amplitude of the radial velocity curve for eight classical Cepheids and two β Cep stars (α Lup and τ1 Lup). This relation is important in the context of the Baade-Wesselink projection factor (Nardetto et al. 2004, 2007), a quantity that is used to derive the distance to the Milky Way and Large Magellanic Cloud Cepheids (Storm et al. 2011a,b). Improving this relation and generalizing it to other pulsators like δ Sct stars is an interesting roadmap to better understand the Baade-Wesselink projection factor. Finally, the use of pulsating stars located below the horizontal branch as distance indicators requires the mode identification as input parameter, and often this is a challenging task to achieve (Poretti et al. 2008). Therefore, the full characterization of bright, short-period δ Sct stars is a key matter in calibrating their period–luminosity (P−L) relation.
In Sect. 2 we briefly present our spectroscopic data. In Sect. 3, we analyse the pulsating frequencies of the two δ Scuti stars. In Sect. 4, we discuss the implication of our data on the derived distances and on the P−L relations. Section 5 is then devoted to the spectroscopic analysis of the two targets in terms of spectral line asymmetry and velocity. In Sect. 6, we compare our results on δ Sct stars with those on classical Cepheids and β Cep stars. We close with some conclusions in Sect. 7.
2. Spectroscopic observations and physical parameters
We observed ρ Pup and DX Cet as additional targets in the framework of the ESO LP185.D-0056. The observations were planned to extend the physical scenario of the δ Sct stars observed with CoRoT.
 |
Fig. 1 Mean profiles of ρ Pup (left panel) and DX Cet (right panel) observed during different nights and folded with the respective pulsation period. Spectral intensities (in continuum units) on the y-axis are arbitrarily shifted to clearly show the profile variations. |
Three-hundred and fifty-nine spectra of ρ Pup were obtained with the High-Accuracy Radial-velocity Planetary Searcher (HARPS; Mayor et al. 2003) in the high-resolution mode (HAM, R = 115 000) on five consecutive nights in January 2013. Observations were performed for a few hours at the end of night, as a backup program. The exposure time was set at 30 s and the signal-to-noise ratio (S/N) was typically about 270. Figure 1 (left panel) shows the behaviour of the mean line profile of each spectrum folded with the pulsational period. Forty-three spectra of DX Cet were obtained with HARPS in the high-efficiency mode (EGGS, R = 80 000) on nine consecutive nights in December 2012. Observations were performed for a few hours at the beginning of night, before the rising of CoRoT targets. The exposure time was set at 300 s and the S/N was usually around 200 (see Fig. 1, right panel). The radial velocity values of ρ Pup were obtained from the HARPS pipeline (Mayor et al. 2003), while those of DX Cet were obtained from the mean line profiles of each spectrum, calculated using the least-squares deconvolution method (Donati et al. 1997).
We estimated the physical parameters of both stars by means of a grid of synthetic spectra. For this purpose we selected four HARPS spectra with a high S/N that were taken at intervals of a quarter of a period starting from the maximum of the radial velocity curve. To save computing time, we reconstructed the synthetic spectra in five 200 Å segments in the range 4000–6650 Å by using the ATLAS9 models and the ATC code (Atmospheric Tools Compilation; Stuetz et al. 2006). Temperature, gravity, metallicity, and microturbulence velocity were allowed to vary in the range 6400 ≤ Teff ≤ 8000 K, 2.6 ≤ log g ≤ 4.8 dex (cgs units), − 1.0 ≤ [Fe/H] ≤ 1.0, and 0 ≤ vmic ≤ 6 km s-1, respectively. We compared the synthetic 200 Å-segments with the observed ones by computing the χ2. At the end of this process, each segment supplied a set of physical parameters obtained by averaging its own best 50 least-squares solutions. In turn, these five sets were averaged to give the physical parameters at the pulsation phase of the HARPS spectrum that we were considering. Then, the averages of the four Teff, log g, [Fe/H], and vmic values corresponding to the four pulsation phases supplied the mean stellar parameters. The typical uncertainties of the parameters supplied by one spectrum were also adopted as the errorbars of the mean stellar parameters.
 |
Fig. 2 Fitting of the Fe I lines in the spectrum of DX Cet. The HARPS spectrum (solid black line) is compared with the synthetic spectrum obtained with Teff = 7100 K, log g = 3.55 dex, vmic = 3.4 km s-1, and [Fe/H] = −0.27 (dashed red). Intensities are normalized to the continuum level. |
The procedure described above supplied Teff = 6650 ± 100 K, log g = 3.42 ± 0.14 dex, [Fe/H] = + 0.20 ± 0.06, and vmic = 4.2 ± 0.7 km s-1 for ρ Pup. Moreover, we measured a projected rotational velocity veq sini = 13 ± 1 km s-1. In the case of DX Cet we obtained Teff = 7200 ± 100 K, log g = 3.58 ± 0.14 dex, vmic = 3.4 ± 0.4 km s-1, [Fe/H] = −0.27 ± 0.06, and veq sini = 7 ± 1 km s-1. Therefore, our spectroscopic analyses yields out that DX Cet has a slight subsolar metallic content, while ρ Pup is confirmed to be a metal-rich star.
To support the [Fe/H] determination of DX Cet in view of the discussion of the P−L relations (see Sect. 4), Fig. 2 shows the agreement between the observed spectrum and the synthetic one calculated with the above parameters.
Hipparcos parallaxes are available for both stars (van Leeuwen 2007): π = 8.65 ± 0.80 mas for DX Cet and π = 51.33 ± 0.15 mas for ρ Pup. DX Cet is located at 116 ± 5 pc and we obtain MV = 1.68 ± 0.20 assuming V = 7.00. ρ Pup is much closer, at 19.48 ± 0.02 pc only, and we derive MV = 1.36 ± 0.01 from the well-established V = 2.81 magnitude. In the case of ρ Pup, the parallax immediately supplied L = 24.0 ± 0.2 L⊙. Combined with the interferometric determination of the radius (R = 3.52 ± 0.07 R⊙; Antoci et al. 2013), this implies Teff = 6820 ± 170 K, in good agreement with our spectroscopic value. Furthermore, we introduced Teff, P, Q = 0.033 d (corresponding to the fundamental radial mode), MV, and the bolometric correction + 0.03 mag (Torres 2010) in the relation (Breger & Bregman 19751)  (1)thus obtaining log g = 3.70 ± 0.02. This latter value agrees within 2σ with ours (log g = 3.42 ± 0.14) and within 1σ with that of Prugniel et al. (2011) (log g = 3.59 ± 0.14). When applying the same approach to DX Cet, Eq. (1) can only supply the condition
(1)thus obtaining log g = 3.70 ± 0.02. This latter value agrees within 2σ with ours (log g = 3.42 ± 0.14) and within 1σ with that of Prugniel et al. (2011) (log g = 3.59 ± 0.14). When applying the same approach to DX Cet, Eq. (1) can only supply the condition  (2)since we have no radius measurement (see also Poretti et al. 2011). Our spectroscopic values match this condition at about 1σ (11.30 ± 0.16). Since in the case of ρ Pup the Teff value is well constrained, this comparison shows that the log g determination is the most critical parameter to evaluate.
(2)since we have no radius measurement (see also Poretti et al. 2011). Our spectroscopic values match this condition at about 1σ (11.30 ± 0.16). Since in the case of ρ Pup the Teff value is well constrained, this comparison shows that the log g determination is the most critical parameter to evaluate.
3. Frequency analyses and nature of pulsations
 |
Fig. 3 Light curves of ρ Pup. Top panel: Eggen (1956) data, 60 measurements from 19 to 26 March 1956. Middle panel: Ponsen (1963) data, 658 measurements from 30 January to 23 April 1961. Bottom panel: Hipparcos data (ESA 1997), 248 measurements from 4 January 1990 to 24 February 1993. |
Least-squares parameters of the HARPS radial velocity curves of ρ Pup (T0 = BJD 2456293.0056) and DX Cet (T0 = BJD 2456272.5889).
3.1. ρ Pup
An exhaustive list of photometric measurements of ρ Pup was reported by Moon & van Antwerpen (2009). Ponsen (1963), Eggen (1956), and Hipparcos (ESA 1997) data are the most suitable for a detailed analysis. Data were obtained in different passbands: Ponsen’s measurements were taken through a blue filter, Eggen’s through a yellow filter, and those of Hipparcos in the wide Hp passband. The folded light curves show asymmetric shapes (Fig. 3). The full amplitudes are 0.13, 0.11, and 0.09 mag, respectively. These values fit the sequence observed at 3858, 4310, 4720, and, 5875 Å, that is, 0.17, 0.14, 0.12, and 0.09 mag (Thulassi Doss 1969). Amplitude ratios (R21) and phase shifts (φ21) were obtained from a least-squares fit with f = 1/P and 2f (P = 0.14088143 d): φ21 = 3.85 ± 0.12 rad and R21 = 0.05 ± 0.01 for Ponsen’s blue data, φ21 = 4.26 ± 0.22 rad and R21 = 0.14 ± 0.03 for Eggen’s yellow data, and φ21 = 4.19 ± 0.10 rad and R21 = 0.09 ± 0.01 for Hipparcos data. Taking into account the different passbands, these Fourier parameters agree excellently and suggest significant departure from a perfect sine-shaped light curve. The Fourier parameters of ρ Pup light curves are typical for HADS stars (Figs. 4 and 6 in Poretti 2001). These stars pulsate in a radial mode (typically the fundamental one) and nonradial modes have a much smaller amplitude. However, the amplitude of ρ Pup is not so large that it could be considered as that of a bona-fide HADS star, and more analyses are necessary.
 |
Fig. 4 Top panel: HARPS radial velocity values of ρ Pup. Different symbols (colours) denote different nights. Cycle-to-cycle variations are clearly visible around the minimum. Bottom panel: HARPS radial velocity values of DX Cet. The solid line is the fit with f1 and three harmonics (Table 1). |
The multiperiodicity of ρ Pup was evident after the detection of clear cycle-to-cycle variations in the radial velocity values obtained with the Coudé Echelle Spectrograph (CES) at the CAT ESO telescope (Mathias et al. 1997). The main oscillation f1 = 7.098168 d-1 was identified as a radial mode and two nonradial modes with frequency 7.8 and 6.3 d-1 were also proposed, but the latter is very uncertain. We used the iterative sine-wave least-squares fitting method (Vaniĉek 1971) to analyse in frequency the radial velocity measurements obtained from the HARPS spectra, determined by the on-line pipeline with an internal error of about 1 m s-1. After the detection of f1, the power spectrum clearly shows a structure centred at 2f1, confirming that the radial velocity curve is asymmetrical, as well. The folded radial velocity curve shows both the asymmetrical shape and cycle-to-cycle variations up to 0.36 km s-1 (Fig. 4). Asymmetry can be evaluated from the maximum, which occurs at phase 0.0, while the minimum occurs before phase 0.50 (filled black circles). After introducing f1 and 2f1 as known constituents, the highest peak in the power spectrum of HARPS data is at f2 = 7.900 d-1, in good agreement with the value obtained from CAT data (i.e., 7.815 d-1; Mathias et al. 1997). However, we note that the spectral windows of both datasets are not adequate to perform a very detailed, self-consistent frequency analysis, since these spectroscopic data were acquired with the goal of studying the dynamics of the dominant pulsation mode. The ground-based photometric data are too noisy to supply useful hints about f2. Even Hipparcos data are unsuitable to search for a small amplitude, short-period additional mode. However, the spectral window of these data is free from the ±1 d-1 aliasing, and we could see, among many others, a peak at 8.860 d-1. Antoci et al. (2013) pointed out 8.82 d-1 as a possible additional frequency. Therefore, we calculated the least-squares fit by considering f2 = 8.860 d-1, but the residual rms (0.067 km s-1) is poorer than that obtained using f2 = 7.900 d-1 (0.041 km s-1). An additional analysis of new data (e.g., Antoci et al., in prep.) may be able to ascertain the true value. We adopted f2 = 7.900 d-1 to describe the dynamical structure of ρ Pup, and the effect of this choice is evaluated at the end of Sect. 5.1.
Table 1 lists the least-squares solution obtained from the HARPS data. The mean value of the radial velocity, 46.74 km s-1, and the 2K value (peak-to-peak amplitude of the radial velocity curve), 9.9 km s-1, agree both excellently with all the literature values. The former suggests that ρ Pup is a single star, the latter that the pulsation is very stable over decades (see also Moon & van Antwerpen 2009). The power spectrum of the residuals shows other modes excited around f1, but the poor spectral window does not allow us to confirm the values proposed by Antoci et al. (2013). In the other parts of the residual power spectrum we were able to observe not only the bunches of peaks related to the higher harmonics of f1, but also those related to the combination terms between f1 (and harmonics) and the additional modes. As stressed by Antoci et al. (2013), these patterns affect the same region in which solar-like oscillations are expected to leave their fingerprints. All these unresolved components contribute to increase the residual rms of the solution.
Neither our radial velocity curve nor Ponsen’s photometry (blue light should be sensitive to this effect) show the bump provoked by a shock wave crossing the atmosphere (Dravins et al. 1977). The emission features in the Mg II lines and the radial velocity curves in the ultraviolet do not show any particular behaviour either (Fracassini et al. 1983). In the top panel of Fig. 4, cycle-to-cycle variations can be noticed especially at the minimum, which seems to occur at different phases. This strange behaviour is only apparent because ρ Pup was observed more at the minimum that at the maximum. For sake of clarity, we investigated the possibility of transient or particular events in the atmosphere dynamics around maximum compression and subsequent expansion. A close examination of the core of the Ca II K line did not reveal any emission during the observations. Therefore, the cycle-to-cycle variations in radial velocity data are definitely unrelated to the variations in the chromospheric activity.
Dall & Frandsen (2002) investigated the presence of the pulsation in the line indices of the Balmer series using the DFOSC instrument mounted at the Danish 1.54 m telescope in La Silla. Indeed, pulsation effects were found, and the authors calculated a ratio of 0.43 for the ratio between the amplitudes of variations in the Hα line and photometry. They considered a half-amplitude of 75 mmag from Eggen’s measurements, which is that derived from a simple inspection of the light curve. We obtained 0.58 for the yellow data and 0.49 for the blue data from the more accurate values resulting from the least-squares fits. Together with the available radial velocity/magnitude amplitude ratio (2K/Δmv = 10.0/0.11 = 91 km s-1 mag-1, see Yang et al. 1987,for a review and summary), these results strengthen the identification of f1 as a radial mode.
3.2. DX Cet
The solution of the radial velocity curve of DX Cet is much simpler than that of ρ Pup. The five components f1 = 9.6197 d-1, 2f1, 3f1, 4f1 and 5f1 are detected in the power spectrum and provide a very satisfactory fit of the radial velocity curve (Table 1 and Fig. 4). The fit of the Hipparcos data (ESA 1997) supplied the Fourier parameters R21 = 0.24 ± 0.02, φ21 = 3.9 ± 0.1, and φ31 = 1.4 ± 0.4 rad. They are typical values for HADS stars (Figs. 4–6 in Poretti 2001). The mean Hp magnitude is 7.077 ± 0.005, which in turn yields V = 7.00 for BT − VT = 0.33 (Bessell 2000). This value and the full amplitude of 0.21 mag as well agree with those reported by Kiss et al. (1999). The 2K/Δmv = 23.1/0.21 = 110 km s-1 mag-1 value supports radial pulsation.
 |
Fig. 5 Illustration of the method applied to derive the centre-of-mass velocity of ρ Pup from the line asymmetries. Points are single observations folded with f1 = 7.098 d-1; the contribution from f2 = 7.900 d-1 has been removed. |
 |
Fig. 6 Amplitude of the RVc curves as a function of the spectral line depth in the case of the two δ Sct stars ρ Pup (lower values), and DX Cet (larger values). In the case of ρ Pup, the solid red line shows the same relation but after removing the nonradial mode. |
4. ρ Pup and DX Cet as distance indicators
The Hipparcos parallaxes and the identification of the pulsation modes of ρ Pup and DX Cet as the fundamental radial ones allowed us to test the P−L relations of HADS stars. There are two P−L relations:  (3)(Poretti et al. 2008), and
(3)(Poretti et al. 2008), and ![\begin{equation} M_V = -1.27 (0.05) - 2.90 (0.07) \log P -0.19 (0.015) [{\rm Fe/H}] \label{feh} \end{equation}](/articles/aa/full_html/2014/01/aa22356-13/aa22356-13-eq108.png) (4)(McNamara 2011). Equation (3) was obtained by using all the short-period (P < 0.20 d) stars that pulsate in the fundamental radial mode and are located in a wide variety of stellar systems. It provides an excellent fit without knowing any other parameter than the period. The metal-dependent term was introduced in Eq. (4) with the goal to determine the same law for HADS and Cepheids and should only be considered when [Fe/H] < 0.0 (McNamara 2011).
(4)(McNamara 2011). Equation (3) was obtained by using all the short-period (P < 0.20 d) stars that pulsate in the fundamental radial mode and are located in a wide variety of stellar systems. It provides an excellent fit without knowing any other parameter than the period. The metal-dependent term was introduced in Eq. (4) with the goal to determine the same law for HADS and Cepheids and should only be considered when [Fe/H] < 0.0 (McNamara 2011).
For DX Cet, Eq. (3) supplies MV = 1.76 ± 0.10 and Eq. (4) MV = 1.64 ± 0.07 for [Fe/H] = −0.27. Both predictions agree excellently with the Hipparcos MV, and hence P = 0.104 d can definitely be identified as the fundamental radial mode. For instance, by assuming that the pulsation is in the first overtone mode, the corresponding fundamental mode would be 0.135 d, and the P−L relations would predict MV = 1.3, which does match the Hipparcos MV. Due to the relevant error on the parallax, McNamara (2011) applied an LK correction (−0.10 mag, then MV = 1.58 ± 0.20; Lutz & Kelker 1973), but the star becomes too bright to fit the value predicted by Eq. (4) in a more satisfactory way.
However, because it is a statistical procedure, the LK correction is powerful when applied to a sample of stars (with the same π) and is much more uncertain when applied to a single case (e.g., Oudmaijer et al. 1998).
The period of ρ Pup is among the longest in the δ Sct sample. Equations (3) and (4) predict similar values without the metal-dependent term, that is, MV = 1.28 ± 0.10 and MV = 1.21 ± 0.07, respectively. The former agrees excellently with the very accurate Hipparcos MV = 1.36 ± 0.01 value, while the latter is slightly outside errorbars. We note that using the [Fe/H] correction in Eq. (4) shifts the calculated value too far (MV = 1.09 ± 0.07) from the observed one. Therefore, this correction definitely does not have to be applied to stars when [Fe/H] > 0.0. Moreover, assuming that f1 is the first radial overtone, we derive MV = 0.87 from the P−L relations, a too bright luminosity for the Hipparcos parallax. This convinced us that ρ Pup is pulsating in the fundamental radial mode.
This achievement adds an important stellar candle to the sample of galactic δ Sct stars with known parallaxes. The current inventory is composed of nine stars (Table 2 in McNamara 2011). However, the identification of the fundamental radial mode is very reliable only for high-amplitude pulsation, that is, the HADS stars DX Cet, AI Vel, and SX Phe. One can add δ Sct itself, since detailed investigations (Templeton et al. 1997) corrected the previous identification of the dominant mode as a radial overtone (Balona et al. 1981). The remaining five cases are rather uncertain, starting with 1 Mon, whose dominant mode has been identified as an overtone (Balona & Stobie 1980). It is instructive to note that the dominant modes of FG Vir and X Cae are nonradial (Zima et al. 2006; Mantegazza et al. 2000): the fundamental radial mode, if it is indeed excited, has to be searched for in the low-amplitude terms, with a wide margin of uncertainty. α Aql (Altair) is a fast rotating star and the nature of the very weak amplitude variations (<0.001 mag) detected with the WIRE satellite can be generated by a wide variety of modes. In particular, there is no convincing evidence that the observed modes are radial ones (Suárez et al. 2005). Finally, no mode identification has been proposed for the small-amplitude variations (0.02 mag) observed for BS Tuc. Therefore, ρ Pup is by far the most convincing case of a δ Sct pulsating in the fundamental radial mode with an accurate Hipparcos parallax.
5. Spectroscopic analysis
We performed a detailed analysis of the high-S/N HARPS spectra of ρ Pup and DX Cet following the procedure described in Nardetto et al. (2006a). We selected 45 spectral lines, taking care that they were not blended.
We extracted radial velocity and line asymmetry curves for all selected lines of all stars. The method we use for the radial velocity (that is the best one to use when the S/N allows it) is the first moment of the spectral line, RVc. The radial velocity curve derived from this method is absolutely independent of the spectral line width and the rotation. This property is extremely valuable for comparing the behaviour of different spectral lines of different pulsating stars. We also derived the spectral line asymmetries A with a very high precision, using an estimator that we call the bi-Gaussian: two analytic semi-Gaussians are fitted to the blue and red part of the spectral line profile. The amount of asymmetry (in percentage) is then given by the comparison of the half-width at half-maximum of each semi-Gaussian (see Nardetto et al. 2006a, their Eqs. (2) and (3)). This definition was well-suited to the data quality.
5.1. ρ Pup
We performed a least-squares fit of the observed values of RVc and A by means of the Fourier series  (5)and by using f1 = 7.098d-1, f2 = 7.900 d-1, f3 = 2f1, f4 = 3f1, and f5 = 4f1. In this way we were able to fold the data on one mode by subtracting the contribution of the other. Figure 5 shows the folded points with f1 of the radial velocities (panel a) and asymmetries (panel b) for the three following lines, CrII 4634.07 (blue), FeI 5410.91 (green), and FeI 6393.60 Å (red), respectively. The corresponding averages of these curves (or similarly B0 values obtained from Eq. (5)) are shown as horizontal lines in panels a and b (in dash-dotted, dashed and solid lines), and are called γ-velocities and γ-asymmetries. The residual systematic scatter is caused by the contamination from very small amplitude modes that are still not identified after f1 and f2. There is an evident anticorrelation: higher velocities correspond to negative asymmetries, low velocities to positive asymmetries. This behaviour is also shown by the trend in the barycenters (big crosses) of the RVc − A loops (Fig. 5, panel c). By plotting for each line the γ-velocity and the γ-asymmetry, we can calculate the parameters of the analytic relation
(5)and by using f1 = 7.098d-1, f2 = 7.900 d-1, f3 = 2f1, f4 = 3f1, and f5 = 4f1. In this way we were able to fold the data on one mode by subtracting the contribution of the other. Figure 5 shows the folded points with f1 of the radial velocities (panel a) and asymmetries (panel b) for the three following lines, CrII 4634.07 (blue), FeI 5410.91 (green), and FeI 6393.60 Å (red), respectively. The corresponding averages of these curves (or similarly B0 values obtained from Eq. (5)) are shown as horizontal lines in panels a and b (in dash-dotted, dashed and solid lines), and are called γ-velocities and γ-asymmetries. The residual systematic scatter is caused by the contamination from very small amplitude modes that are still not identified after f1 and f2. There is an evident anticorrelation: higher velocities correspond to negative asymmetries, low velocities to positive asymmetries. This behaviour is also shown by the trend in the barycenters (big crosses) of the RVc − A loops (Fig. 5, panel c). By plotting for each line the γ-velocity and the γ-asymmetry, we can calculate the parameters of the analytic relation  (6)thus obtaining α0 = −0.12 ± 0.01 km s-1 and β0 = 47.49 ± 0.07 km s-1 (Fig. 5, panel d). Following Nardetto et al. (2008), the centre-of-mass velocity of the star is defined as Vγ⋆ = β0 = 47.49 ± 0.07 km s-1(i.e., the γ-velocity corresponding to a null γ-asymmetry). We note that the contributions of f2 = 7.900 d-1 to the γ-velocity and γ-asymmetry are much less important than those of f1, which means that they affect the spectral line asymmetries in a marginal way. The k-term, defined as k = ⟨Vγ⟩ i − Vγ⋆ = 47.0± 0.1 − 47.5± 0.1 = −0.5 ± 0.1 km s-1, where ⟨Vγ⟩ i is the γ-velocity averaged over the 45 spectral lines. We briefly discuss the k-term problem in Sect. 5.3.
(6)thus obtaining α0 = −0.12 ± 0.01 km s-1 and β0 = 47.49 ± 0.07 km s-1 (Fig. 5, panel d). Following Nardetto et al. (2008), the centre-of-mass velocity of the star is defined as Vγ⋆ = β0 = 47.49 ± 0.07 km s-1(i.e., the γ-velocity corresponding to a null γ-asymmetry). We note that the contributions of f2 = 7.900 d-1 to the γ-velocity and γ-asymmetry are much less important than those of f1, which means that they affect the spectral line asymmetries in a marginal way. The k-term, defined as k = ⟨Vγ⟩ i − Vγ⋆ = 47.0± 0.1 − 47.5± 0.1 = −0.5 ± 0.1 km s-1, where ⟨Vγ⟩ i is the γ-velocity averaged over the 45 spectral lines. We briefly discuss the k-term problem in Sect. 5.3.
The next step of the spectroscopic analysis is to measure the velocity gradient within the atmosphere of the star. In Nardetto et al. (2007), we have shown that the line depth (taken at the minimum radius phase) is a good indicator of the line-forming regions. We use this definition of the line depth (hereafter D) in the following. In this case, the photosphere corresponds to a null line depth. By comparing the 2K amplitude (defined as the amplitude of the first-moment radial velocity curve, hereafter ΔRVc) with the depth of the 45 spectral lines selected, one can in principle directly measure the atmospheric velocity gradient (at least in the part of the atmosphere where the lines form). For ρ Pup, we found the following relation (see also Fig. 6): ![\begin{equation} \Delta RV_{\mathrm{c}} = [0.95 \pm 0.49] D + [8.84 \pm 0.19] \:\mathrm{km\: s}^{-1} . \label{cinque} \end{equation}](/articles/aa/full_html/2014/01/aa22356-13/aa22356-13-eq138.png) (7)This relation (in which we define the slope and the zero-point by a0 and b0, respectively) can be used to derive the Baade-Wesselink projection factor following the semi-theoretical approach presented in Guiglion et al. (2013). The projection factor is used to convert the radial velocity into the pulsation velocity in the Baade-Wesselink methods of distance determination. It is composed of three terms: p = p0fgradfo − g (Nardetto et al. 2007). First, the geometric projection factor, p0, is mainly related to the limb-darkening of the star. The linear limb-darkening law of the continuum intensity profile of the star provided by Claret & Bloemen (2011) is I(cos(θ)) = 1 − uR + uRcos(θ), where uR is the limb darkening of the star in R-band and θ is the angle between the normal of the star and the line of sight. For ρ Pup we found uR = 0.484 (considering the rounded values Teff = 6500 K, log g = 3.5, vmic = 4 km s-1, and Z = 0.0). Using the relation linking p0 to uR:
(7)This relation (in which we define the slope and the zero-point by a0 and b0, respectively) can be used to derive the Baade-Wesselink projection factor following the semi-theoretical approach presented in Guiglion et al. (2013). The projection factor is used to convert the radial velocity into the pulsation velocity in the Baade-Wesselink methods of distance determination. It is composed of three terms: p = p0fgradfo − g (Nardetto et al. 2007). First, the geometric projection factor, p0, is mainly related to the limb-darkening of the star. The linear limb-darkening law of the continuum intensity profile of the star provided by Claret & Bloemen (2011) is I(cos(θ)) = 1 − uR + uRcos(θ), where uR is the limb darkening of the star in R-band and θ is the angle between the normal of the star and the line of sight. For ρ Pup we found uR = 0.484 (considering the rounded values Teff = 6500 K, log g = 3.5, vmic = 4 km s-1, and Z = 0.0). Using the relation linking p0 to uR: 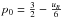 (Getting 1934; Hadrava et al. 2009), we found p0 = 1.416. In this determination of the geometric projection factor, we assumed (as done previously for Cepheids) that the limb-darkening variation within the lines (Nardetto et al. 2007) and that the geometric projection factor time-dependency in the R-band (Nardetto et al. 2006b) are negligible.
(Getting 1934; Hadrava et al. 2009), we found p0 = 1.416. In this determination of the geometric projection factor, we assumed (as done previously for Cepheids) that the limb-darkening variation within the lines (Nardetto et al. 2007) and that the geometric projection factor time-dependency in the R-band (Nardetto et al. 2006b) are negligible.
Then, fgrad depends on the spectral line considered: fgrad = b0/(a0D + b0) (Nardetto et al. 2007, their Eq. (3)). For ρ Pup, it ranges from 0.94 (D = 0.22) to 0.98 (D = 0.55). For a typical depth in our sample of D = 0.4, we find fgrad = 0.96 ± 0.01. Finally, there is a linear relation between fo − g (correction to the projection factor due to the differential velocity between the optical and gas layers at the photosphere of the star) and log P: fo − g = [ − 0.023 ± 0.005] log P + [0.979 ± 0.005] (derived using classical Cepheids; Nardetto et al. 2007). When we apply this relation for ρ Pup as in Guiglion et al. (2013) for the δ Sct stars AI Vel and β Cas, we found fo − g = 1.00 ± 0.02. The final value of the projection factor of ρ Pup is thus p = p0fgradfo − g = 1.36 ± 0.02.
From a methodological point of view, it is interesting to note that we find a0 = 0.88 ± 0.49 and b0 = 8.56 ± 0.19 (i.e., a decrease of the slope and zero-point of the relation by 8% and 3%, respectively) when fitting the original data with f1 and harmonics alone. In turn, this increases the value of fgrad, and consequently that of p, by only 0.2%. In a similar way, there is no change in the parameters of Eq. (7) and a non-significant decrease of the zeropoint of Eq. (6) (from 8.86 to 8.84 km s-1) when using f2 = 8.86 d-1 instead of 7.90 d-1 (see Sect. 3.1).
5.2. DX Cet
We applied the same analysis to DX Cet. Figure 7 (panels a and b) shows the radial velocity and line asymmetry curves for the three lines FeI 4213.65, FeI 5393.17, and FeI 6393.60 Å. We found the same anticorrelation between the γ-velocity and the γ-asymmetry: ![\begin{eqnarray*} V_\gamma(i)= [ -0.15\pm 0.03] A_\gamma(i) + [25.75\pm 0.06]. \end{eqnarray*}](/articles/aa/full_html/2014/01/aa22356-13/aa22356-13-eq170.png) The centre-of-mass velocity of the star is then Vγ⋆ = β0 = 25.75 ± 0.06 km s-1 and the k-term is k = ⟨Vγ⟩ − Vγ⋆ = 25.7± 0.1 − 25.7± 0.1 ≃ 0.0 ± 0.1kms-1.
The centre-of-mass velocity of the star is then Vγ⋆ = β0 = 25.75 ± 0.06 km s-1 and the k-term is k = ⟨Vγ⟩ − Vγ⋆ = 25.7± 0.1 − 25.7± 0.1 ≃ 0.0 ± 0.1kms-1.
For the atmospheric velocity gradient we found (Fig. 6) ![\begin{equation} \Delta RV_{\mathrm{c}} = [1.15 \pm 0.48] D + [21.62 \pm 0.14] \:\mathrm{km\: s}^{-1}, \end{equation}](/articles/aa/full_html/2014/01/aa22356-13/aa22356-13-eq173.png) (8)which corresponds to a velocity gradient or fgrad correction of the projection factor ranging from 0.97 (D = 0.12) to 0.99 (D = 0.49). The average value fgrad = 0.98 ± 0.01 (D = 0.30) was used. From the rounded values available in Claret & Bloemen (2011,Teff = 7000 K, log g = 3.5, vmic = 2.0 km s-1 and Z = −0.3, we obtained uR = 0.474 and a geometric projection factor p0 = 1.421. Considering, as for ρ Pup, fo − g = 1.00 ± 0.02, we finally found a Baade-Wesselink projection factor p = 1.39 ± 0.02 for DX Cet.
(8)which corresponds to a velocity gradient or fgrad correction of the projection factor ranging from 0.97 (D = 0.12) to 0.99 (D = 0.49). The average value fgrad = 0.98 ± 0.01 (D = 0.30) was used. From the rounded values available in Claret & Bloemen (2011,Teff = 7000 K, log g = 3.5, vmic = 2.0 km s-1 and Z = −0.3, we obtained uR = 0.474 and a geometric projection factor p0 = 1.421. Considering, as for ρ Pup, fo − g = 1.00 ± 0.02, we finally found a Baade-Wesselink projection factor p = 1.39 ± 0.02 for DX Cet.
6. Comparing δ Scuti stars with β Cep stars and classical Cepheids
Our HARPS sample is composed of stars with a good phase coverage and for which we were able to measure the spectral line asymmetry properly. We have eight classical Cepheids (R TrA, S Cru, Y Sgr, ζ Gem, β Dor, RZ Vel, ℓ Car, and RS Pup; Nardetto et al. 2008), two δ Sct stars (ρ Pup and DX Cet; this paper), and the β Cep star α Lup (Nardetto et al. 2013). Moreover, we have other cases. AI Vel has an incomplete phase coverage that prevented us from measuring the γ-asymmetry, although we were able to measure the atmospheric velocity gradient and the projection factor. β Cas is rotating too fast to measure the spectral line asymmetry or derive the atmospheric velocity gradient with a good precision. Thus, we determined the projection factor only with a large uncertainty (Guiglion et al. 2013). The classical Cepheid X Sgr shows spectral line splitting due probably to a shockwave in the atmosphere (Mathias et al. 2006). The β Cep τ1 Lup shows significant nonradial modes (Nardetto et al. 2013) and we were unable to consistently apply the bi-Gaussian method to measure the line asymmetry.
 |
Fig. 8 Same as Figs. 5d and 7d, but including the results obtained for classical Cepheids (averaged over eight stars) and α Lup (β Cep star). The horizontal lines at the bottom show the corresponding γ-asymmetry ranges. |
 |
Fig. 9 Velocity gradient in the atmosphere of the stars as a function of the amplitude of the RVc curves. |
In Fig. 8, we compare Vγ(i) = α0 Aγ(i) + β0 relations between the γ-velocities and the γ-asymmetries (after correcting for the zero-point) found for ρ Pup and DX Cet, with previous results obtained for the β Cep star α Lup and for the eight classical Cepheids mentioned above. It is remarkable that the results obtained for δ Scuti stars and classical Cepheids are consistent, while α Lup shows a different behaviour (steeper slope of the relation). We also note that α Lup has only negative γ-asymmetries (at least over the 55 spectral lines considered in Nardetto et al. 2013). It is currently very difficult to interpret this behaviour, but at least qualitatively, we can conclude that there is a particular physical mechanism that probably affects the α Lup spectral lines asymmetry, while this is not the case for the δ Scuti and Cepheid stars.
For the k-term quantity, we found k = −0.5 km s-1 and k = 0 km s-1 for ρ Pup and DX Cet, respectively. These values are consistent with those found for Cepheids (values ranging from 0 to − 1 km s-1 depending on the period of the star, Nardetto et al. 2013). By using a Cepheid in an eclipsing binary system (Ppuls = 3.8 d, Porb = 309 d), Pilecki et al. (2013) independently found a blue-shifted value k = −0.59 km s-1. On the other hand, α Lup shows a red-shifted value k = 2.2 km s-1.
Figure 9 shows the slope a0 (from the ΔRVc = a0D + b0 relation) as a function of the 2K-amplitude (i.e., b0). The results obtained for δ Scuti stars, β Cep stars, and classical Cepheids are compared. The case of τ1 Lup must be considered separately, as previously mentioned in Nardetto et al. (2013). This star indeed shows a reverse atmospheric velocity gradient, which means that a line forming in the upper part of the atmosphere has a 2K-velocity amplitude lower than a line forming closer to the photosphere. This might be because of the nonradial mode detected in the spectroscopic data. On the other hand, ρ Pup has a null velocity gradient for a similar velocity amplitude of about b0 ≃ 10 km s-1. It has to be confirmed, but it seems that stars with a dominant radial mode and with b0 lower than 22.5 km s-1 have a null atmospheric velocity gradient (dashed line in Fig. 9). Conversely, we can convincingly consider a linear trend (solid line in the figure) for 2K-amplitudes larger than 22.5 km s-1: a0 = [0.29 ± 0.04] b0 − [6.61 ± 1.36].
The comparison of the projection factors within our sample is also very interesting. In the framework of our project, we determined the Baade-Wesselink projection factor for four δ Sct stars: ρ Pup (p = 1.36 ± 0.02), DX Cet (p = 1.39 ± 0.02), AI Vel (p = 1.44 ± 0.05), and β Cas (p = 1.41 ± 0.25). Figure 10 shows that all these values excellently fit the extension toward short periods of the relation found for Cepheids, that is, p = [ − 0.08 ± 0.05] log P + [1.31 ± 0.06] (Nardetto et al. 2009). This result seems more robust than the similar one obtained by Laney & Joner (2009), who used an indirect method based on the comparison of geometric and pulsation parallaxes. On the other hand, the projection factor of the β Cep star α Lup is 8σ higher than the relation (Fig. 10). By omitting α Lup, we can determine the following relation common to δ Sct stars and classical Cepheids: ![\begin{equation} p = [-0.08 \pm 0.01] \log P + [1.31 \pm 0.01], \end{equation}](/articles/aa/full_html/2014/01/aa22356-13/aa22356-13-eq204.png) (9)which is similar to the one derived for Cepheids only, but more precise (the reduced χ2 is 0.97).
(9)which is similar to the one derived for Cepheids only, but more precise (the reduced χ2 is 0.97).
 |
Fig. 10 Baade-Wesselink projection factor as a function of the period for different kinds of pulsating stars. The δ Scuti stars indicated as blue diamonds are, by increasing periods: β Cas, DX Cet, AI Vel and ρ Pup. |
However, we have to stress some methodological points. First, in the projection factor decomposition (p = p0fgradfo − g), the third component, fo − g, was extrapolated for the δ Scuti stars (not for α Lup, for which we used a dedicated hydrodynamical model), while the fgrad quantity was derived directly and independently from observations. We also recall that the geometric projection factor, p0, is directly linked to the limb-darkening and thus to the fundamental parameters of the stars. Second, for the Cepheids, the projection factors are consistent with the cross-correlation method of the radial velocity determination. For DX Cet and ρ Pup, the line depth considered for the fgrad correction is typical (i.e., averaged over all lines considered in our sample), which means that the derived projection factors are in principle very close to those to be used in the cross-correlation method. For α Lup, AI Vel, and β Cas, there is no velocity gradient in the atmosphere and the projection factor is the same regardless of the line considered, and thus is consistent with the cross-correlation method. There remains only the fact that in the cross-correlation method a Gaussian is fitted to the cross-correlated spectral line profile, which in principle reduces the value of the projection factor by few percents compared with that based on the first-moment method (Nardetto et al. 2006a). Reducing the projection factor for short pulsators in Fig. 10 by a few per cent will basically not change the relative position of α Lup and our qualitative conclusion that the period–projection factor relation seems to straightly link δ Scuti stars and classical Cepheids. Third, the fast rotation of some δ Scuti stars (as well as the inclination of their rotation axis) can affect the projection factor by 10% or even more (Guiglion et al. 2013). However, the δ Scuti stars in our sample show veqsini values lower than 13 km s-1, except for β Cas with veqsini ≃ 75 km s-1.
Even if we were able to derive both the Baade-Wesselink projection factors and the centre-of-mass velocities for the eleven pulsating stars in our sample, an effort (both observational and theoretical) has still to be made to understand the spectral line asymmetry properly. For classical Cepheids, the hydrodynamical models reproduce the observed velocities and even the atmospheric velocity gradient very well (Fokin 1996; Nardetto et al. 2004, 2007). Nevertheless, currently, there is no hydrodynamical model of pulsating stars that can correctly reproduce the γ-velocities and γ-asymmetries. In particular, we emphasize that the k-term quantity cannot be explained by a Van Hoof effect (Mathias et al. 1993, 1995). In Fig. 11, we show the Van Hoof diagram for the three spectral lines of Sect. 5.1 for ρ Pup.
The Van Hoof effect is not detected because there is no phase shift between the radial velocities of the different spectral lines (i.e., no loops). We also find that the two curves have a slope close to one, indicating a null atmospheric velocity gradient, as already mentioned. Nevertheless, the zero-points of the two curves are shifted, as a result from the γ-velocity offsets (Fig. 5, panel a). The possible physical causes of these offsets (e.g., additional modes) are under analysis.
 |
Fig. 11 Van Hoof diagram for ρ Pup. The radial velocity curve associated to the Fe I 5410.91 (green) and Fe I 6393.60 Å (red) spectral line profiles is plotted as a function of the same quantity, but for Cr II 4634.07. The solid line corresponds to the identity function. There is no Van Hoof effect detected (no loops), while the γ-velocity effect is clearly seen (y-axis offsets of the curves). |
7. Conclusions
We presented HARPS high-resolution spectra of ρ Pup and DX Cet, thus increasing our sample to eleven stars. Among them, the β Cep star α Lup shows an interesting positive value of 2.2 km s-1 for the k-term, while other kinds of pulsating stars have negative values (ranging from − 1 to 0 km s-1). We also found that ρ Pup shows the same 2K velocity amplitude (8.84 ± 0.19 km s-1) regardless of the spectral line considered in our sample (45 lines), while this is not the case for stars with amplitudes larger than 22.5 km s-1, where a trend is indeed found as a function of the the line depth. This behaviour, if confirmed, would mean that the atmospheric velocity gradient correction on the Baade-Wesselink projection factor, fgrad, is equal to 1.0 for any type of pulsating star as soon as its 2K velocity amplitude is lower than 22.5 km s-1. Finally, we found that the period–projection factor relation might be common to classical Cepheids and δ Scuti, while the β Cep star α Lup stands at 8σ above the relation.
The excitation of different pulsation modes (fundamental and overtone radial, pressure and gravity nonradial) usually makes the use of δ Sct stars as distance indicators problematic. For ρ Pup, our analysis of light and radial velocity curves identified the dominant mode as the fundamental radial one. Because it is a very bright star with an accurate Hipparcos parallax, ρ Pup can be now considered as the best standard candle for the δ Sct class. The Hipparcos absolute magnitude gives us a luminosity log L/L⊙ = 1.38. Combined with Teff = 6650–6800 K, this implies that ρ Pup is very close to the red border of the instability strip, probably leaving the central part where most of the HADS stars are located (Pamyatnykh 2000).
Moreover, from the Hipparcos parallax (π = 7.02 ± 0.17 mas), the mean radius of R = 3.52 ± 0.07 R⊙ (Antoci et al. 2013), and our value of the projection factor p = 1.36 together with our radial velocity curve (in particular, 2K = 8.8 km s-1), we were able to infer an absolute angular diameter variation of 11 μas (or 0.7%). Unfortunately, there are no K photometric observations of ρ Pup that cover a full pulsation cycle to which one might apply the infrared surface brightness relation and confirm these findings.
Acknowledgments
The authors wish to thank the anonymous referee for useful comments. E.P. and M.S. acknowledge financial support from the Italian PRIN-INAF 2010 Asteroseismology: looking inside the stars with space- and ground-based observations. M.R. scknowledges financial support from the FP7 project SPACEINN: Exploitation of Space Data for Innovative Helio- and Asteroseismology. V.S.S. is an Aspirant PhD fellow of the Fonds voor Wetenschappelijk Onderzoek, Vlaanderen (FWO), Belgium. N.N. and E.P. acknowledge the Observatoire de la Côte d’Azur for the one-month grant that has allowed EP to work at OCA in April and May 2013.
References
- Antoci, V., Handler, G., Grundahl, F., et al. 2013, MNRAS, 435, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L., & Stobie, R. S. 1980, MNRAS, 190, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L., Dean, J. F., & Stobie, R. S. 1981, MNRAS, 194, 125 [NASA ADS] [Google Scholar]
- Bessell, M. S. 2000, PASP, 112, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 1974, ApJ, 192, 75 [Google Scholar]
- Breger, M., & Bregman, J. N. 1975, ApJ, 200, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cousins, A. W. 1951, Observatory, 71, 199 [NASA ADS] [Google Scholar]
- Dall, T. H., & Frandsen, S. 2002, A&A, 386, 964 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dravins, D., Lind, J., & Särg, K. 1977, A&A, 54, 381 [NASA ADS] [Google Scholar]
- Eggen, O. J. 1956, PASP, 68, 238 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Fokin, A. B., Gillet, D., & Breitfellner, M. G. 1996, A&A, 307, 503 [NASA ADS] [Google Scholar]
- Fracassini, M., Pasinetti, L. E., Castelli, F., Antonello, E., & Pastori, L. 1983, Ap&SS, 97, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Getting, I. A. 1934, MNRAS, 95, 139 [NASA ADS] [Google Scholar]
- Guiglion, G., Nardetto, N., Mathias, P., et al. 2013, A&A, 550, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadrava, P., Slechta, M., & Skoda, P. 2009, A&A, 507, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiss, L. L., Csak, B., Thomson, J. R., & Szatmary, K. 1999, IBVS, 4660, 1 [NASA ADS] [Google Scholar]
- Kurtz, D. W. 1976, ApJS, 32, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Laney, C. D., & Joner, D. J. 2009, AIPC, 1170, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, T. E., & Kelker, D. H. 1973, PASP, 85, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Mantegazza, L., Zerbi, F. M., & Sacchi, A. 2000, A&A, 354, 112 [NASA ADS] [Google Scholar]
- Mathias, Ph., & Gillet, D. 1993, A&A, 278, 511 [NASA ADS] [Google Scholar]
- Mathias, Ph., Gillet, D., Fokin, A. B., & Chadid, M. 1995, A&A, 298, 843 [NASA ADS] [Google Scholar]
- Mathias, Ph., Gillet, D., Aerts, C., & Breitfellner, M. G. 1997, A&A, 327, 1077 [NASA ADS] [Google Scholar]
- Mathias, Ph., Gillet, D., Fokin, A. B., et al. 2006, A&A, 457, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McNamara, D. H. 2011, AJ, 142, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Moon, T., & van Antwerpen, C. 1997, JAAVSO, 37, 3 [NASA ADS] [Google Scholar]
- Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&AP, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006a, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Fokin, A., Mourard, D., et al. 2006b, A&A, 454, 327 [Google Scholar]
- Nardetto, N., Mourard, D., Mathias, P., et al. 2007, A&A, 471, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Stoekl, A., Bersier, D., et al. 2008, A&A, 489, 1255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Kervella, P., et al. 2009, A&A, 502, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mathias, P., Fokin, A., et al. 2013, A&A, 553, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oudmaijer, R. D., Groenewegen, M. A. T., & Schrijver, H. 1998, MNRAS, 294, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Pamyatnykh, A. A. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. H. Montgomery, ASP Conf. Ser., 210, 215 [Google Scholar]
- Pilecki, B., Graczyk, D., Pietrzynski, G., et al. 2013, MNRAS, 436, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Ponsen, J. 1963, Bull. Astron. Inst. Netherlands, 17, 44 [NASA ADS] [Google Scholar]
- Poretti, E. 2001, A&A, 371, 986 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poretti, E., Clementini, G., Held, E. V., et al. 2008, ApJ, 685, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Poretti, E., Rainer, M., Weiss, W. W., et al. 2011, A&A, 528, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, Ph., Vauglin, I., & Koleva, M. 2011, A&A, 531, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. 1991, ApJ, 102, 589 [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011a, A&A, 534, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011b, A&A, 534, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuetz, Ch., Bagnulo, S., Jehin, E., et al. 2006, A&A, 451, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez, J. C., Bruntt, H., & Buzasi, D. 2005, A&A, 438, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Templeton, M. R., McNamara, B. J., Guzik, J. A., et al. 1997, AJ, 114, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- Thulassi Doss, A. 1969, Kodaikanal Obs. Bull., 191 [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaniĉek, P. 1971, Ap&SS, 12, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, S., Walker, G. A. H., & Bennett, P. 1987, PASP, 99, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Zima, W., Wright, D., Bentley, J., et al. 2006, A&A, 455, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Least-squares parameters of the HARPS radial velocity curves of ρ Pup (T0 = BJD 2456293.0056) and DX Cet (T0 = BJD 2456272.5889).
All Figures
 |
Fig. 1 Mean profiles of ρ Pup (left panel) and DX Cet (right panel) observed during different nights and folded with the respective pulsation period. Spectral intensities (in continuum units) on the y-axis are arbitrarily shifted to clearly show the profile variations. |
| In the text | |
 |
Fig. 2 Fitting of the Fe I lines in the spectrum of DX Cet. The HARPS spectrum (solid black line) is compared with the synthetic spectrum obtained with Teff = 7100 K, log g = 3.55 dex, vmic = 3.4 km s-1, and [Fe/H] = −0.27 (dashed red). Intensities are normalized to the continuum level. |
| In the text | |
 |
Fig. 3 Light curves of ρ Pup. Top panel: Eggen (1956) data, 60 measurements from 19 to 26 March 1956. Middle panel: Ponsen (1963) data, 658 measurements from 30 January to 23 April 1961. Bottom panel: Hipparcos data (ESA 1997), 248 measurements from 4 January 1990 to 24 February 1993. |
| In the text | |
 |
Fig. 4 Top panel: HARPS radial velocity values of ρ Pup. Different symbols (colours) denote different nights. Cycle-to-cycle variations are clearly visible around the minimum. Bottom panel: HARPS radial velocity values of DX Cet. The solid line is the fit with f1 and three harmonics (Table 1). |
| In the text | |
 |
Fig. 5 Illustration of the method applied to derive the centre-of-mass velocity of ρ Pup from the line asymmetries. Points are single observations folded with f1 = 7.098 d-1; the contribution from f2 = 7.900 d-1 has been removed. |
| In the text | |
 |
Fig. 6 Amplitude of the RVc curves as a function of the spectral line depth in the case of the two δ Sct stars ρ Pup (lower values), and DX Cet (larger values). In the case of ρ Pup, the solid red line shows the same relation but after removing the nonradial mode. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 for DX Cet. |
| In the text | |
 |
Fig. 8 Same as Figs. 5d and 7d, but including the results obtained for classical Cepheids (averaged over eight stars) and α Lup (β Cep star). The horizontal lines at the bottom show the corresponding γ-asymmetry ranges. |
| In the text | |
 |
Fig. 9 Velocity gradient in the atmosphere of the stars as a function of the amplitude of the RVc curves. |
| In the text | |
 |
Fig. 10 Baade-Wesselink projection factor as a function of the period for different kinds of pulsating stars. The δ Scuti stars indicated as blue diamonds are, by increasing periods: β Cas, DX Cet, AI Vel and ρ Pup. |
| In the text | |
 |
Fig. 11 Van Hoof diagram for ρ Pup. The radial velocity curve associated to the Fe I 5410.91 (green) and Fe I 6393.60 Å (red) spectral line profiles is plotted as a function of the same quantity, but for Cr II 4634.07. The solid line corresponds to the identity function. There is no Van Hoof effect detected (no loops), while the γ-velocity effect is clearly seen (y-axis offsets of the curves). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


