| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 47 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201935523 | |
| Published online | 30 July 2019 | |
The complex chemistry of hot cores in Sgr B2(N): influence of cosmic-ray ionization and thermal history
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
Bonn,
Germany
e-mail: [email protected]
2
Departments of Chemistry, University of Virginia,
Charlottesville,
VA
22904,
USA
3
Departments of Astronomy, University of Virginia,
Charlottesville,
VA
22904,
USA
4
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
Received:
22
March
2019
Accepted:
6
June
2019
Context. As the number of complex organic molecules (COMs) detected in the interstellar medium increases, it becomes even more important to place meaningful constraints on the origins and formation pathways of such chemical species. The molecular cloud Sagittarius B2(N) is host to several hot molecular cores in the early stage of star formation, where a great variety of COMs are detected in the gas phase. Given its exposure to the extreme conditions of the Galactic center (GC) region, Sgr B2(N) is one of the best targets to study the impact of environmental conditions on the production of COMs.
Aims. Our main goal is to characterize the physico-chemical evolution of Sgr B2(N)’s sources in order to explain their chemical differences and constrain their environmental conditions.
Methods. The chemical composition of Sgr B2(N)’s hot cores, N2, N3, N4, and N5 is derived by modeling their 3 mm emission spectra extracted from the Exploring Molecular Complexity with ALMA (EMoCA) imaging spectral line survey performed with the Atacama Large Millimeter/submillimeter Array (ALMA). We derived the density distribution in the envelope of the sources based on the masses computed from the ALMA dust continuum emission maps. We used the radiative transfer code RADMC-3D to compute temperature profiles and inferred the current luminosity of the sources based on the COM rotational temperatures derived from population diagrams. We used published results of 3D radiation-magnetohydrodynamical (RMHD) simulations of high-mass star formation to estimate the time evolution of the source properties. We employed the astrochemical code MAGICKAL to compute time-dependent chemical abundances in the sources and to investigate how physical properties and environmental conditions influence the production of COMs.
Results. The analysis of the abundances of 11 COMs detected toward Sgr B2(N2-N5) reveals that N3 and N5 share a similar chemical composition while N2 differs significantly from the other sources. We estimate the current luminosities of N2, N3, N4, and N5 to be 2.6 × 105 L⊙, 4.5 × 104 L⊙, 3.9 × 105 L⊙, and 2.8 × 105 L⊙, respectively. We find that astrochemical models with a cosmic-ray ionization rate of 7 × 10−16 s−1 best reproduce the abundances with respect to methanol of ten COMs observed toward Sgr B2(N2-N5). We also show that COMs still form efficiently on dust grains with minimum dust temperatures in the prestellar phase as high as 15 K, but that minimum temperatures higher than 25 K are excluded.
Conclusions. The chemical evolution of Sgr B2(N2-N5) strongly depends on their physical history. A more realistic description of the hot cores’ physical evolution requires a more rigorous treatment with RMHD simulations tailored to each hot core.
Key words: stars: formation / ISM: individual objects: Sagittarius B2(N) / astrochemistry / ISM: molecules / cosmic rays / molecular processes
© M. Bonfand et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
To date more than 200 molecules1 have been discovered in the interstellar medium (ISM) or in circumstellar envelopes of evolved stars (see, e.g., McGuire 2018). These molecules are mostly organic (that is they contain at least one atom of carbon) and among them about one third are composed of six or more atoms and are considered as complex in terms of astrochemistry (Herbst & van Dishoeck 2009). As the inventory of complex organic molecules (COMs) expands, they have attracted a lot of attention, in particular recently due to their possible link to amino acids, the chemical building blocks of proteins which contribute to life as we know it on Earth. Numerous extraterrestrial amino acids have been discovered in meteorites (Botta & Bada 2002) and one in comets (Altwegg et al. 2016). However, the simplest amino acid, glycine (NH2CH2COOH), has not yet been detected in the ISM. Nonetheless, many COMs have been discovered toward the warm and dense regions associated with high-mass star formation, known as hot cores, by investigating their rotational spectrum at (sub)millimeter wavelengths. Despite these numerous detections, the precise origins of these complex species, as well as the mechanisms leading to their formation, are still subject to debate. The rise of astrochemical models solving coupled kinetic rate equations built from networks of thousands of chemical reactions has allowed significant progress in our understanding of the complex chemistry in the ISM. For instance, it has been shown that dust-grain chemical processes play an important role in the formation of COMs (Garrod & Herbst 2006; Garrod et al. 2007; Garrod 2008; Herbst & van Dishoeck 2009), the abundances of some of which cannot currently be explained by gas-phase chemistry. Therefore, it is crucial to better understand the chemical processes that take place in the interstellar ices at early time and low temperature to explain the later high gas-phase chemical abundances observed toward regions forming high-mass stars. The numerous COMs detected toward hot molecular cores, right after desorption from the dust grains into the gas phase, may be used to trace the physical conditions of their parent molecular cloud since they hold information on the collapse history.
The Galactic center (GC) cloud Sagittarius B2 (Sgr B2), located at ~100 pc in projection from the central supermassive black hole Sgr A*, exhibits one of the richest molecular inventories observed to date and thus appears to be an excellent target to search for COMs and probe interstellar chemistry. Many of the first detections of interstellar molecules at radio and (sub)mm wavelengths were made toward Sgr B2 (Menten 2004), in particular some of the most complex species detected in the ISM, such as acetic acid CH3COOH (Mehringer et al. 1997), glycolaldehyde CH2 (OH)CHO (Hollis et al. 2000), acetamide CH3C(O)NH2 (Hollis et al. 2006), aminoacetonitrile NH2CH2CN (Belloche et al. 2008), and N-methylformamide CH3NHCHO (Belloche et al. 2017). With a mass of ~107 M⊙ in a diameter of ~40 pc (Lis & Goldsmith 1990), Sgr B2 is also one of the most prominent regions forming high-mass stars in our Galaxy. Its two main centers of star-formation activity, Sgr B2(N)orth and Sgr B2(M)ain, both host a cluster of (ultra)compact HII regions (Mehringer et al. 1993; Gaume et al. 1995; De Pree et al. 1998, 2015) and several 6.7 GHz class II methanol masers (Caswell 1996), which uniquely mark the locations of massive young protostellar objects.
Given its exceptional characteristics and its strong, ongoing star-formation activity (e.g., Bonfand et al. 2017; Sánchez-Monge et al. 2017; Ginsburg et al. 2018), Sgr B2 stands out from the other clouds located in the central molecular zone (CMZ; inner 200–500 pc) of the Galaxy. Indeed, recent studies find that despite its large reservoir of dense gas, the CMZ appears to be deficient in star formation overall in comparison to other high-mass star-forming regions in the galactic disk with similar density and age (e.g., Rathborne et al. 2014; Kruijssen et al. 2014; Kauffmann et al. 2017; Walker et al. 2018). This apparent inactivity suggests that the critical density for star formation in the CMZ is ~107 cm−3 (see, e.g., Rathborne et al. 2014; Kruijssen et al. 2014; Kauffmann et al. 2017; Ginsburg et al. 2018; Barnes et al. 2019), much higher than in the rest of the galactic disk (~104 cm−3, see, e.g., Lada et al. 2010, 2012). The environmental conditions in the CMZ are also known to be extreme compared to the rest of the galactic disk, in particular with a stronger interstellar radiation field (ISRF, Lis et al. 2001; Clark et al. 2013), and higher cosmic-ray fluxes (Oka et al. 2005; van der Tak et al. 2006; Yusef-Zadeh et al. 2007; Clark et al. 2013). The exceptional physical conditions of the CMZ provide an excellent test of current models of high-mass star formation and can advance our understanding of star-formation mechanisms within extreme environments. Due to its proximity to the GC, Sgr B2 provides us with an interesting case study to investigate how extreme physical and environmental factors influence the high-mass star formation process, whether they tend to enhance or suppress star formation activity.
In a previous analysis of the 3 mm imaging line survey Exploring Molecular Complexity with ALMA (EMoCA) we reported the detection of three new hot cores, Sgr B2(N3), N4, and N5 (Bonfand et al. 2017). These new hot cores are all associated with 6.7 GHz class II methanol masers and Sgr B2(N5) also with an ultra-compact HII (UCHII) region. From the analysis of the 3 mm emission spectra observed toward the new hot cores, we derived their chemical composition, revealing the presence of up to 23 different species of which about half are complex (Bonfand et al. 2017). Because the spectrum observed toward the main hot core Sgr B2(N1) is close to the confusion limit and severely affected by line blending, here we focus our analysis on the four other hot cores Sgr B2(N2-N5). That all of these hot cores most probably originate from the same cloud material, with similar chemical and physical properties (e.g., initial chemical abundances, gas-to-dust mass ratio), makes comparing them with each other particularly meaningful. By comparing the predictions of astrochemical models with the observations, we want to identify the most efficient pathways leading to the formation of COMs (see for instance Belloche et al. (2017) for the case of N-methylformamide) and explore the impact of the environment on the production of these complex species.
The extreme environmental conditions of the CMZ most likely also affect the chemistry of Sgr B2(N)’s hot cores. In particular, in dense regions shielded from direct UV irradiation, cosmic rays play an important role in the gas-phase chemistry as they represent the main source of ionization. The direct ionization of atomic and molecular hydrogen results in the formation of secondary electrons (see Eq. (1)), which can cause additional ionization (Goldsmith & Langer 1978). In addition, collisions of H and H2 with secondary electrons inside dense clouds lead to the production of ultra-violet (UV) radiation (Prasad & Tarafdar 1983). This cosmic ray-induced UV field can dissociate molecules, both in the gas phase and on dust-grain surfaces inside the clouds, where external UV photons cannot penetrate.
The so-called cosmic-ray ionization rate (CRIR), ζH2, describes the total rate of ionization per H2 molecule per second, including secondary ionizations. The first theoretical determination of the CRIR was made by Hayakawa et al. (1961) and revised later by Spitzer & Tomasko (1968). The latter derived a lower limit of ζH = 6.8 × 10−18 s−1, which corresponds to ζH2 ~ 1.3 × 10−17 s−1 according to the simple approximation ζH2 ~ 2ζH (Glassgold & Langer 1974) commonly used for dense gas in which most hydrogen is in its molecular form. This value of ζH2 is often referred to as the standard CRIR. An accurate measurement of the CRIR is difficult to obtain through direct detection because low-energy particles (<1 GeV) are prevented from entering the heliosphere by the solar wind, making them not directly measurable from Earth (Parker 1958). However, the CRIR can be estimated with astrochemical models, by analyzing specific molecules whose formation and destruction processes are driven by cosmic rays. Given its relatively simple chemistry, the H3+ ion is commonly used as an indirect probe for constraining the CRIR:
 (1)
(1)
 (2)
(2)
Recently, Le Petit et al. (2016) used the Meudon photodissociation region (PDR) code to reproduce the large H3+ column densities observed in the diffuse gas component of the line of sight to the CMZ (n = 100 cm−2, T = 200–500 K). They derived a CRIR of ζH2 ~1 – 11 × 10−14 s−1 that is in line with the values that Indriolo et al. (2015) obtain from an analysis of data for OH+, H2O+, and H3O+ observed by Herschel for various clouds in the CMZ. However, it has been shown that low energy cosmic-ray particles can penetrate diffuse clouds easily but that they lose energy on their path toward the center of denser clouds, as they ionize and excite the matter they travel through (Umebayashi & Nakano 1981). Many previous studies have sought to quantify the attenuation of the cosmic-ray flux in dense clouds (see, e.g., Padovani et al. 2009; Rimmer et al. 2012; Neufeld & Wolfire 2017). However, despite the numerous attempts to constrain the CRIR in diverse regions of the ISM, huge uncertainties still remain. Therefore, the CRIR is usually treated as a free parameter in astrochemical models, ranging from ζH2 ~ 10−17 s−1 to 10−14 s−1. The impact of variations in the CRIR value on calculated chemical abundances can then be used to identify functional probes for the CRIR in dense clouds and determine the ionization rate that best reproduces the observations (see, e.g., Albertsson et al. 2018; Allen et al. 2018).
In this paper we use the chemical kinetics code, MAGICKAL (Garrod 2013), coupled with the radiative transfer code RADMC-3D (Dullemond et al. 2012) and the published results of radiation-magnetohydrodynamical (RMHD) simulations of high-mass star formation (Peters et al. 2011) to model the physico-chemical evolution of the four dense molecular cores, Sgr B2(N2-N5). We investigate the impact of physical properties and environmental conditions on the formation of specific COMs observed toward Sgr B2(N2-N5) in order to constrain the CRIR and the minimum dust temperature reached during the prestellar phase that best characterize Sgr B2(N).
The article is structured as follows: the observations and methods of analysis are presented in Sect. 2. In Sect. 3 we determine the physical properties of Sgr B2(N2-N5) and build up the physical models used as inputs for the chemical modeling discussed in Sect. 4. The results of our standard models are presented in Sect. 5. In Sect. 6 we discuss the impact of varying the minimum dust temperature and the CRIR on the production of COMs. We compare the model results to the observations to constrain the environmental conditions in Sgr B2(N2-N5). Finally our main results are summarized in Sect. 7.
2 Observations and methods of analysis
2.1 The EMoCA survey
The EMoCA imaging spectral line survey was conducted with ALMA in its cycles 0 and 1 at high angular resolution (~1.6′′) with a sensitivity of ~3 mJy beam−1 per 488 kHz (1.7–1.3 km s−1) wide channel. The survey is divided into five spectral setups covering the frequency range between 84.1 and 114.4 GHz (Table E.1). At these frequencies, the size (half power beam width – HPBW) of the primary beam of the 12 m antennas varies between 69′′ at 84 GHz and 51′′ at 114 GHz (Remijan 2015). The phase center is located half way between the two main hot molecular cores Sgr B2(N1) and N2 (αJ 2000 = 17h47m19.s87, δJ 2000 = −28o22′16.″0). A detailed description of the observations, the calibration, and the imaging procedures is presented in Belloche et al. (2016).
2.2 Data reduction
Belloche et al. (2016) used the spectra observed toward the main hot cores Sgr B2(N1-N2) to split the line and continuum emission into separated datacubes. In comparison, the spectra observed toward the hot cores Sgr B2(N3-N5) contain significantly less emission lines (that is more emission-free channels, Bonfand et al. 2017). We used the spectra extracted toward their peak positions to split the spectral lines from the continuum emission more accurately, using the CLASS2 software. In each spectral window of each setup, a first-order baseline is subtracted to the channels that are free of strong line emission to separate the spectral lines from the continuum. The noise level measured in the new continuum-subtracted spectra is listed in Table E.1 along with the values measured by Belloche et al. (2016) in the channel maps of the full field of view for comparison.
2.3 Radiative transfer modeling of the line survey
In order to derive the chemical composition of Sgr B2(N3-N5) we performed a radiative transfer modeling of the EMoCA line survey. Given the high densities observed in the hot cores (~107 cm−3, Bonfand et al. 2017), collisions in the gas phase are frequent enough for the local thermodynamic equilibrium (LTE) approximation to be valid. We used Weeds (Maret et al. 2011), which is part of the CLASS software, to produce LTE synthetic spectra that we compared to the observed continuum-subtracted spectra, after correction for the primary beam attenuation. Weeds solves the radiative transfer equation, taking into account the finite angular resolution of the interferometer, the line opacity, line blending, and the continuum background. The spectroscopic predictions used to model the spectra mainly originate from the CDMS (Cologne Database for Molecular Spectroscopy, Endres et al. 2016) and JPL (Jet Propulsion Laboratory, Pearson et al. 2010) catalog. They are the same as in Belloche et al. (2016, 2017) and Müller et al. (2016), except for ethanol, methanol, and methyl cyanide, for which we used new CDMS predictions. Each molecule is modeled separately, adjusting the following parameters: column density, rotational temperature, angular size of the emitting region (assumed to be Gaussian), velocity offset with respect to the systemic velocity of the source, and linewidth (full width at half maximum – FWHM). For each molecule, a population diagram is plotted to derive the rotational temperature and 2D Gaussians are fit to integrated intensity maps of unblended transitions to measure the size of the emitting region. 1D-Gaussian fits to emission lines are used to derive the linewidth and velocity offset. The column density is adjusted manually until a good fit to the data is obtained. Finally, the contribution from all species is added linearly to build up the complete synthetic spectrum. More details about the methods of analysis can be found in Bonfand et al. (2017).
3 Physical properties of Sgr B2(N)’s hot cores
In order to model the time-dependent chemical composition of Sgr B2(N)’s sources, we need to determine their physical properties and characterize their time evolution, from the cold ambient cloud phase (that is prior to the free-fall collapse of the cloud) to the dense and warm hot core phase. In this section we derive the physical properties of the sources (H2 column density, mass, density, size, temperature, and luminosity) based on the observations. In particular, temperature and density will be used to derive the physical profiles used as inputs for the chemical modeling (Sect. 4).
3.1 H2 column densities and masses
We derived H2 column densities from the dust thermal emission measured in the ALMA continuum emission maps toward each source, using the following equation (Bonfand et al. 2017):
 (3)
(3)
with  = 2.8 the mean molecular weight per hydrogen molecule (Kauffmann et al. 2008), mH the mass of atomic hydrogen,
= 2.8 the mean molecular weight per hydrogen molecule (Kauffmann et al. 2008), mH the mass of atomic hydrogen,  the solid angle of the synthesized ALMA beam, Bν (Td) the Planck function at the dust temperature Td = 150 K (assuming Td ~ Tg, the gas kinetic temperature, see Sect. 3.2), κν the dust absorption coefficient per unit of mass density of gas (in cm2 g−1), and
the solid angle of the synthesized ALMA beam, Bν (Td) the Planck function at the dust temperature Td = 150 K (assuming Td ~ Tg, the gas kinetic temperature, see Sect. 3.2), κν the dust absorption coefficient per unit of mass density of gas (in cm2 g−1), and  the peak flux density measured in Jy beam−1 toward each hot core in the ALMA continuum emission maps, after correction for the primary beam attenuation and the free-free contribution (Bonfand et al. 2017). The dust mass opacity is given by the power law:
the peak flux density measured in Jy beam−1 toward each hot core in the ALMA continuum emission maps, after correction for the primary beam attenuation and the free-free contribution (Bonfand et al. 2017). The dust mass opacity is given by the power law:
 (4)
(4)
with κ0 the reference dust mass absorption coefficient at the frequency ν0. In our previous analysis (Bonfand et al. 2017) we derived a dust emissivity exponent β of 1.2 ± 0.1 from the combined analysis of our ALMA data and the dust continuum emission map obtained with the submillimeter array (SMA) at 343 GHz (Qin et al. 2011). According to the simulations of dust coagulation in cold dense cores conducted by Ossenkopf & Henning (1994), a dust emissivity exponent of β = 1.2 suggests an intermediate dust opacity spectrum between the models of dust grains without ice mantles and those with thin ice mantles (see Fig. F.1). Here we adopt the model with grains without ice mantle and for gas densities of 106 cm−3, which corresponds to a dust emissivity exponent of β = 1.3, with κ0 = 0.0199 cm2 g−1 (of gas) at ν0 = 230 GHz (that is λ0 = 1.3 mm, see Fig. F.1).
Table 1 shows the H2 column densities calculated at Td = 150 K for Sgr B2(N2-N5). In the case of Sgr B2(N3), which is not detected in the ALMA continuum maps at 3 mm (Bonfand et al. 2017), we used the peak flux density measured by Sánchez-Monge et al. (2017) at 242 GHz in ALMA data obtained at 0.4′′ resolution.
For each hot core, we derived the gas mass of the envelope contained in the 1.6′′ ALMA mean synthesized beam (or 0.4′′ for Sgr B2(N3)), from the H2 column density as follows (Hildebrand 1983):
 (5)
(5)
with D = 8.34 kpc the distance to Sgr B2(N) from the Sun (Reid et al. 2014) and R the radius of the mean ALMA synthesized beam:
 (6)
(6)
with θb = 1.6′′ the mean synthesized beam of the ALMA observations (or 0.4′′ for Sgr B2(N3)). The resulting masses are given in Table 1.
Physical properties of four hot cores embedded in Sgr B2(N).
3.2 Source sizes and temperatures
In our previous analysis of Sgr B2(N) we derived the size of the COM emission region, θs, for the hot cores Sgr B2(N3-N5) (Bonfand et al. 2017). For each source we selected in the observed spectra the transitions that have a high signal-to-noise ratio (S/N), are well reproduced by the LTE model, and are not severely contaminated by other species. We fit 2D Gaussians to their integrated intensity maps to derive the emission size. We derived deconvolved sizes of 1.0 ± 0.3′′ and 1.0 ± 0.4′′ for Sgr B2(N4) and N5 respectively, which are slightly smaller than the size of Sgr B2(N2) (~1.2′′, with values ranging between 0.8′′ and 1.5′′; Belloche et al. 2016, 2017). Sgr B2(N3) is more compact, with an emission size of 0.4′′. For each hot core the radius of theemitting region, r0, is computedusing Eq. (6) and is given in Table 1.
From the COM emission Bonfand et al. (2017) also derived excitation temperatures by plotting population diagrams based on the transitions that are well detected and not severely contaminated by lines from other species. At high densities, where the LTE approximation is valid, the level populations can be described by a single excitation temperature, Trot. We found that Trot varies from ~145 to 190 K for Sgr B2(N3-N5). The temperatures for Sgr B2(N2) were determined by Belloche et al. (2016, 2017) and Müller et al. (2016). We assume that the excitation temperature is equal to the kinetic temperature and we adopt a gas temperature T0 of 150 K at the radius r0 (see Table 1).
3.3 Luminosity and temperature profile
We used theradiative transfer code RADMC-3D (version 0.41), to compute dust temperature profiles in the envelopes of Sgr B2(N2-N5), based on their current masses (Sect. 3.1) and temperatures (Sect. 3.2). RADMC-3D performs radiative transfer calculations using the Monte-Carlo method for a given dust distribution and computes the associated dust temperatures. Each source is modeled as a single protostar surrounded by a 1D spherically symmetric envelope with a radius of 106 au (that is 4.8 pc), divided into 5 × 104 cells. The protostar is defined as a point-source (that is its radius is not taken into account) and we assumed simple black body radiation by setting its effective temperature. For simplicity we adopted a single type of interstellar grains and do not include scattering. We used the dust opacities from Ossenkopf & Henning (1994) for dust without ice mantle and coagulated with gas densities of 106 cm−3 as found to best fit Sgr B2(N)’s dust properties (Sect. 3.1).
The dust mass density in the envelope of each source is assumed to follow a power-law distribution:
 (7)
(7)
with ρ0 the dust mass density at the radius r0. We assume α = −1.5, holding for a free-falling envelope (Shu 1977). Assuming the following gas-to-dust mass ratio, Md = Mg∕χd with χd = 100, we can write:
 (8)
(8)
with Mg(R) the gas mass inside of R derived in Sect. 3.1. By replacing ρd(r) by its expression (Eq. (7)) we obtain:
 (9)
(9)
Finally, by integrating Eq. (9) we obtain:
 (10)
(10)
The resulting dust mass densities, ρ0, are given in Table 1. The dust mass density profiles derived in the envelope of Sgr B2(N2-N5) using Eq. (7) is shown in Fig. F.2. Given the high densities reached in the envelopes, photon packages may get trapped inside optically thick regions, considerably slowing down the simulations. To prevent this effect, we used the Modified Random Walk Method (MRW, Fleck & Canfield 1983) that allows RADMC-3D to predict where the photon package will go next and save computation time.
Finally, for each source the luminosity of its central protostar is adjusted until the calculated dust temperature in the envelope matches the observational constraint, Td(r0) = T0. This gives us an estimate of the current luminosity of the sources. Figure 1 shows the dust temperature profiles computed by RADMC-3D in the envelope of the sources along with the total luminosities of their central protostars, which are also listed in Table 1.
3.4 Protostellar evolution
In Sect. 3.3 we estimated the current luminosity of Sgr B2(N2-N5). In order to model the time-dependent chemical evolution of these sources, we need to determine the evolution of their protostellar properties, from the earlier stage of star formation, when a young protostar has just formed and started to warm up the surrounding gas. To this aim, we use published results from theoretical simulations of high-mass star formation.
Peters et al. (2011) report the results from the first 3D radiation-magnetohydrodynamical (RMHD) simulations of high-mass star formation including ionization feedback. They modeled the free-fall collapse of a magnetized rotating molecular cloud containing 1000 M⊙. The central core, with a gas density of ρ = 1.27 × 10−20 g cm−3 within a radius of 0.5 pc, is surrounded by an envelope characterized by a density distribution ∝ r−1.5. They assumed an initial temperature of 30 K. After the first 20 kyr of simulation, many sink particles are formed, simulating a group of young stars all contributing to the radiative feedback (see their Fig. 1a, run E). In the initial accretion phase the first sink particle reaches a high accretion rate >10−3 M⊙ yr−1, which reduces to ~10−4 M⊙ yr−1 after 0.7 Myr (see their Fig. 1b, run E). At the end of the simulation, the first sink particle is by far the most massive one. Although its accretion rate drops significantly when secondary sink particles form, it continues accreting material until the end of the simulation. Based on the accretion rate evolution of the most massive sink particle, without taking into account the influence of the formation of secondary particles, we approximated the relation Ṁ (t), characterizing the time-dependent evolution of the accretion rate for a young high-mass protostar. Figure 2a (dashed line) shows the accretion rate as a function of time for a protostar that starts accreting material from its surrounding envelope at t0 = 0. By integrating the relation Ṁ (t) we obtain the protostellar mass as a function of time, M (t). Figure 2b (dashed line) shows that after 106 yr the protostar reaches a final mass of about 30 M⊙.
In order to estimate the time-dependent evolution of Sgr B2(N2-N5)’s luminosities, L (t), from the relation M (t) (Fig. 2b), we used the mass-luminosity relation derived by Hosokawa & Omukai (2009) for spherically accreting protostars with a constant accretion rate of Ṁ = 10−4 M⊙ yr−1 (see Fig. F.3). The resulting total luminosity is plotted as a function of time in Fig. 2c (dashed line). It shows that after 106 yr the protostar reaches a final luminosity of ~105 L⊙, which is not high enough to reproduce the luminosities estimated for Sgr B2(N2-N5) (up to 3.9 × 105 L⊙, Sect. 3.3). In order to form more massive and thus more luminous protostars, we simply assumed that the accretion rate does not drop below 10−4 M⊙ yr−1 (Fig. 2a, solid line). Using this simple assumption, protostars with masses >102 M⊙ and luminosities up to ~2 × 106 L⊙ are formed after 106 yr (Figs. 2b and c, solid lines). We used the relation L (t) (Fig. 2c) to estimate the age, tsource, of Sgr B2(N2-N5) based on their current luminosity (see Table 1).
The approach described in this section provides us with a simple model of the physical evolution of young high-mass protostars. Applied to Sgr B2(N2-N5) it allows us to investigate the evolution of their chemical composition using astrochemical models. Ourphysical model is based on the simple assumption that in all sources, objects with similar final mass are formed, which might not be the case in reality (see discussion in Sect. 6.6). Our treatment is not intended to reflect the complexity of cloud-collapse dynamics but rather to provide a simple framework in which to model the behavior of the cloud chemistry under such conditions. Only a deeper analysis of the whole Sgr B2 molecular cloud would provide a more accurate model for individual sources (see for instance the 3D radiative transfer model of Schmiedeke et al. 2016, which addresses the physical structure of Sgr B2 as a whole, from 45 pc down to 100 au).
 |
Fig. 1 Dust temperature profiles computed for Sgr B2(N2-N5) using RADMC-3D, assuming a dust mass density distribution proportional to r−1.5 (Fig. F.2). The observational constraint Td(r0) = T0 used to estimate the current luminosity of each source is plotted with errorbars (1σ). |
 |
Fig. 2 Panela: accretion rate evolution for a young high-mass protostar approximated from the RMHD simulations of Peters et al. (2011; dashed lines). Panel b: time evolution of the protostar’s mass derived from its accretion rate, Ṁ (t) (panel a, dashed line). Panel c: time evolution of the protostar’s total luminosity derived from its mass, M (t) (panel b, dashed line), using the Hosokawa & Omukai (2009) mass-luminosity relation (Fig. F.3). Inall panels the solid line shows the result obtained when keeping a constant accretion rate (10−4 M⊙ yr−1) after ~6 × 104 yr. |
3.5 The physical model
Modeling the time-dependent chemical evolution of Sgr B2(N2-N5) requires to know their physical structure and evolution over the whole star formation formation process, including the early cold phase preceding the hot core phase. However, the early initial stage of high-mass star formation, prior to the protostar’s formation, and its timescale are still poorly known. Based on the fraction of star-forming versus quiescent clumps detected in the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL), Csengeri et al. (2014) estimated an upper limit of ~7.5±2.5 × 104 yr for the quiescent deeply embedded phase ( ~ 4 × 105 cm−3) prior to the onset of free-fall collapse. Wilcock et al. (2012) derived statistical lifetimes for starless infrared dark clouds (IRDCs) of ~2.3 × 105 yr from the Herschel Infrared Galactic Plane (HI-GAL) survey. This is a factor three longer than the prestellar phase described by Csengeri et al. (2014) for objects with densities ranging from ~104 to 105 cm−3. More recently, Jeffreson et al. (2018) performed theoretical calculations to estimate the lifetimes of giant molecular clouds based on the time-scales derived for the large-scale dynamical processes that affect the ISM. For clouds located in the CMZ, at galactocentric radii from ~45 to 120 pc, they estimated median cloud lifetimes of 1.4–3.9 × 106 yr.
~ 4 × 105 cm−3) prior to the onset of free-fall collapse. Wilcock et al. (2012) derived statistical lifetimes for starless infrared dark clouds (IRDCs) of ~2.3 × 105 yr from the Herschel Infrared Galactic Plane (HI-GAL) survey. This is a factor three longer than the prestellar phase described by Csengeri et al. (2014) for objects with densities ranging from ~104 to 105 cm−3. More recently, Jeffreson et al. (2018) performed theoretical calculations to estimate the lifetimes of giant molecular clouds based on the time-scales derived for the large-scale dynamical processes that affect the ISM. For clouds located in the CMZ, at galactocentric radii from ~45 to 120 pc, they estimated median cloud lifetimes of 1.4–3.9 × 106 yr.
We divide the early evolutionary phase of high-mass star formation into two distinct stages based on their physical conditions. The first stage traces the evolution of the chemistry for 1 Myr, which corresponds to an intermediate time between the IRDC starless phase derived by Wilcock et al. (2012) and the molecular cloud lifetime determined by Jeffreson et al. (2018). This stage is characterized by low densities and low temperatures in the envelope of the source (see Sect. 3.5.1), which undergoes quasi-static contraction leading to the formation a centrally peaked prestellar core. The second stage starts with the ignition of a young accreting protostar warming up its surrounding envelope. In this stage the envelope undergoes a free-fall collapse (see Sect. 3.5.2), starting from the conditions reached at the end of the first stage. The two stages of our physical model along with the associated timescales are schematized in Fig. 3. The physical properties characterizing each stage are computed in Sects. 3.5.1 and 3.5.2.
3.5.1 Quasi-static contraction
The quasi-static contraction phase prior to the free-fall collapse comprises the evolution of density, visual extinction, and temperature in the envelope of Sgr B2(N2-N5) from tstart = − 1 × 106 yr to t0 = 0, corresponding to the formation of the stellar embryo and the onset of the free-fall collapse. For simplicity we assumed that the radius does not change and remains constant throughout this phase (that is we look at the evolution of the density, visual extinction, and temperature of a given parcel of gas at a fixed radius, rstart, see also Sect. 3.5.2). The quasi-static contraction phase starts at low density, with nH-start = 3 × 103 cm−3 where nH is the total hydrogen density (that is nH = n(H) + 2n(H2)), and low visual extinction, with Av-start = 2 mag. These are the same initial condition as in Garrod (2013) and subsequent papers. We made the simple assumption that density and extinction at a given radius increase linearly as a function of time in log–log space (see Fig. F.4 and Table E.4).
In orderto characterize the behavior of the dust temperature during the cold, low density phase preceding the warming up of the envelope, we adopted the visual-extinction-dependent treatment presented in Garrod & Pauly (2011). Assuming that the rate of cooling of the dust is equal to the rate of radiative heating due to its exposure to a standard interstellar radiation field, ISRF = 1 G0 in units of the Draine field (Draine 1978), they found that for Av < 10 mag, the dust temperature can be described with a third-order polynomial:
 (11)
(11)
Following Garrod & Pauly (2011), at higher visual extinctions (Av > 10 mag) we use the dust temperature profile given by Zucconi et al. (2001).
For all sources, the quasi-static contraction phase starts with Td-start = 16 K because Av-start = 2 mag, and the dust temperature then decreases as the visual extinction increases. However, dust temperature measurements carried out at infrared wavelengths with the Herschel Space Observatory report somewhat higher temperatures toward the GC region (20–28 K, see Sect. 6.2). Therefore, in order to keep the model physically meaningful and account for the higher dust temperatures expected toward the GC region, we defined an arbitrary minimum temperature, Tmin, which represents the lowest temperature that is allowed in the chemical simulations (see also Sect. 4.2). In Fig. 4 we plotted the dust temperature as a function of time for Sgr B2(N2-N5) with different Tmin. The gas kinetic temperature, Tg, is held constant throughout the whole quasi-static contraction phase, with Tg = Tmin.
The physical conditions (density, temperature, and visual extinction) achieved at the end of the quasi-static contraction phase are given for each source in Table 2. They represent the initial conditions for the free-fall collapse.
 |
Fig. 3 Two-stage physical model assumed for the time evolution of Sgr B2(N2-N5). The physical properties derived at the boundaries of each stage are shown in boxes (see also Table 2). The parameters that are common to all sources are highlighted in boldface. The evolution of the physical parameters during each stage is indicated in green with arrows. The evolution of Td during the first stage depends on the adopted minimum dust temperature (see Sect. 3.5.1). |
 |
Fig. 4 Dust temperature as a function of time during the quasi-static contraction phase (Eq. (11)). Temperatures are computed for a constant radius, r = rstart, and for threedifferent Tmin. |
3.5.2 Free-fall collapse
In our physical models, the free-fall collapse phase starts with the ignition of a young high-mass protostar. As the newly formed protostar evolves, it starts heating up the surrounding gas and accretes material from its envelope. In order to characterize the evolution of the physical conditions in the collapsing envelope, we trace the trajectory of a parcel of gas gradually infalling toward the central protostar with the free-fall velocity
 (12)
(12)
with Mg(r) the mass of gas inside of r. The starting point, rstart, of the parcel of gas is chosen such that it reaches r0 at t = tsource (see Sect. 3.4), partaking in the free-fall governed by the enclosed mass. The trajectory, r(t), of a parcel of gas infalling through the envelope of Sgr B2(N2-N5) with the free-fall speed vff is shown in Fig. F.5.
We derived the gas density along the trajectory of the free-falling parcel of gas from the power-law profile:
 (13)
(13)
with nH = 2  , the density of total hydrogen, and n0 the reference density at r0. For simplicity we neglected the time variation of nH(r) during the free-fall collapse phase. From Eq. (8), we can write:
, the density of total hydrogen, and n0 the reference density at r0. For simplicity we neglected the time variation of nH(r) during the free-fall collapse phase. From Eq. (8), we can write:
 (14)
(14)
which, in combination with Eq. (13) yields:
 (15)
(15)
The visual extinction along the trajectory of the free-falling parcel of gas is computed from the gas density as follows (Bohlin et al. 1978):
 (16)
(16)
with rinit the initial radius of the source envelope computed such that nH(rinit) = nstart; thus  (see Table 1). During the free-fall collapse phase the visual extinction increases with density, until Av-max = 500 mag. For simplicity we neglected the time variation of Av(r) during the free-fall collapse.
(see Table 1). During the free-fall collapse phase the visual extinction increases with density, until Av-max = 500 mag. For simplicity we neglected the time variation of Av(r) during the free-fall collapse.
As the protostar’s total luminosity rises, the temperatures in the envelope increase, progressively dominating the dust heating over the external radiation field. Based on the evolution of the luminosity over time, L (t) (Sect. 3.1), we computed for each source dust temperature profiles for different luminosities, that is at different stages of star formation (see Fig. F.6). Based on the relation r (t) (Fig. F.5) we derived Td (r) the temperature evolution along the trajectory of a parcel of gas free-falling through the envelopes of Sgr B2(N2-N5) during the collapse phase. The free-fall collapse phase stops when the temperature reaches Tmax = 400 K. Given the high densities and high visual extinctions reached in the envelope of Sgr B2(N2-N5), gas and dust temperatures are assumed to be well coupled during the free-fall collapse phase such that Tg (r) = Td (r).
The gas density, temperature, and visual extinction computed along the trajectory of the parcel of gas infalling through the envelopes of Sgr B2(N2-N5) are plotted in Figs. F.7 and F.8. The physical conditions (radius, density, temperature, and visual extinction) achieved at the end of the free-fall collapse phase are given for each source in Table 2.
Parameters of the physical models for Sgr B2(N2-N5).
4 Chemical modeling
4.1 A three-phase astrochemical code
In order to interpret the COM abundances observed toward Sgr B2(N)’s hot cores (see Sect. 5.1), we used the astrochemical code MAGICKAL (Model for Astrophysical Gas and Ice Chemical Kinetics and Layering, Garrod 2013) to calculate chemical abundances in the envelopes of Sgr B2(N2-N5). MAGICKAL is a single-point model that allows us to simulate in one stage the time-dependent physico-chemical evolution of a given source, from the early cold phase of the star-formation process to the warm up of the dense cores. The calculated chemical abundances characterize a range of distances from the cold extended region to the warmer innermost part of the protostellar collapsing envelope.
The chemical network is based on that of Belloche et al. (2017). It contains 1333 distinct chemical species of which neutrals can exist either as gas-phase, grain-surface, or ice-mantle species, while charged species are considered in the gas phase only. The grain surface is defined as the outermost layer of ice that resides on top of the other ice layers or directly onto the grain surface itself. The rest of the ice mantle, composed of the deeper ice layers below the ice surface, is treated as a separate phase. The network comprises 13 374 chemical reactions and processes, which include gas-phase ion-molecule reactions and the related electronic recombination of the resulting protonated ions. Photodissociation and photoionization processes are also included, affecting both the gas-phase and grain-surface chemistry with UV photons from either the ambient radiation field or the CR-induced UV field. Gas-phase and ice-surface chemistry are coupled through the accretion of gas-phase material onto the grains, which may be released back into the gas phase via thermal or non-thermaldesorption processes (including chemical reactive desorption, Garrod et al. 2007). Diffusion allows reactions within the mantle as well as exchange of chemical species between surface and mantle via swapping mechanisms. Details on the chemical processes and reactions rates can be found in Garrod et al. (2008), Garrod & Pauly (2011), and Garrod (2013).
The coupled gas-phase, dust-grain surface, and ice-mantle chemistry is solved using the modified rate-equation approach of Garrod (2008) to account for stochastic effects in the surface chemistry. In addition, the model uses the grain-surface back-diffusion correction of Willis & Garrod (2017), and assumes a single dust-grain size of 0.1 μm.
The initial gas-phase material is assumed to be mostly composed of atoms and atomic ions, except for H2. Initial abundances are taken from Garrod (2013). As Sgr B2(N)’s hot cores presumably originate from material with the same elemental abundances, the same initial abundances are used for all hot cores.
Grid of chemical models.
4.2 The chemical models
In this section we present the grid of chemical models (see Table 3) run to investigate the time-dependent chemical evolution of Sgr B2(N2-N5) and explore the influence of environmental conditions on the calculated chemical abundances. The first parameter we vary is the minimum dust temperature, Tmin, that can be reached in the simulations, in particular during the cold quasi-static contraction phase prior to the onsetof the free-fall collapse (see also Sect. 3.5.1). The minimum dust temperature adopted in the chemical simulations is critical because the production of the main ice constituents (H2O, CO, CO2, and CH3OH), essential to the formation of COMs, is highly sensitive to the dust temperature. At low temperatures (~10 K), mainly hydrogenation reactions are important on the surface of dust grains. As the temperature increases, the surface diffusion rates of heavier species become more important leading to a massive increase in the surface production of simple species by addition of radicals (OH, HCO, NH, NH2, CH3, CH2OH, CH3O). However, hydrogen atoms evaporate quickly and hydrogenation reactions become less efficient because the rate of desorption of H is much faster than the rate of reaction between H atoms. In order to explore the impact of the minimum dust temperature on the production of COMs we run “low temperature” models with Tmin = 10 K, “intermediate temperature” models with Tmin = 15 K, and finally, to better represent the higher temperatures expected toward the GC, “high temperature” models with Tmin = 20 K (see Sect. 6.2).
The second aspect explored in the chemical simulations is the impact of the CRIR on the production of COMs. We ran chemical simulations using CRIRs ranging from the standard value  = 1.3 × 10−17 s−1 to 1000
= 1.3 × 10−17 s−1 to 1000 = 1.3 × 10−14 s−1. Given the uncertainties on the column-density dependence of the CRIR in dense regions (see Sect. 6.3), we assumed for simplicity that no attenuation occurs in the envelope of the sources. Due to its location in the CMZ, Sgr B2 is also known to be affected by X-ray emission (see, e.g., Terrier et al. 2018). As the effects of X-rays are often considered to be similar to cosmic ray-related processes (see, e.g., Viti et al. 2003), here the total ionization rate may be seen as a combination of both effects.
= 1.3 × 10−14 s−1. Given the uncertainties on the column-density dependence of the CRIR in dense regions (see Sect. 6.3), we assumed for simplicity that no attenuation occurs in the envelope of the sources. Due to its location in the CMZ, Sgr B2 is also known to be affected by X-ray emission (see, e.g., Terrier et al. 2018). As the effects of X-rays are often considered to be similar to cosmic ray-related processes (see, e.g., Viti et al. 2003), here the total ionization rate may be seen as a combination of both effects.
For each hot core we ran a grid of 18 models, one for each set of physical parameters (CRIR and Tmin, see Table 3). The interstellar radiation field is held constant throughout the model grid, assuming a standard value of 1 G0. The influence of the ISRF strength on the chemical simulations is discussed in Appendix D.
5 Results
5.1 Observed chemical composition of the hot cores
We used Weeds as described in Sect. 2.3 to derive the chemical composition of Sgr B2(N3-N5) by modeling the continuum subtracted emission spectra observed toward each source. We present the results obtained for 11 COMs that include N-, O-, and S-bearing species, to provide a broad census of the chemical composition of the sources. The parameters of the best-fit LTE models are listed in Table E.2along with the column densities derived for each molecule. The column densities derived for Sgr B2(N2) are also given for comparison (Belloche et al. 2016, 2017; Müller et al. 2016). In the case of methyl cyanide (CH3CN), we investigated its isotopologs 13CH3CN and CH CN because the vibrational ground statetransitions of CH3CN are optically thick. We assumed the isotopic ratio [CH3CN]/[13CH3CN] = [CH3CN]/[CH
CN because the vibrational ground statetransitions of CH3CN are optically thick. We assumed the isotopic ratio [CH3CN]/[13CH3CN] = [CH3CN]/[CH CN] = 21 derived by Belloche et al. (2016) to obtain the column density of CH3CN.
CN] = 21 derived by Belloche et al. (2016) to obtain the column density of CH3CN.
The column densities derived for the 11 COMs in the four hot cores are plotted in Fig. 5a along with their uncertainties, estimated as described in Appendix A. In order to compute abundances relative to H2 (Fig. 5b), we used the H2 column densities derived for the compact region with warm dense gas from which the COM emission arises (see Table E.3). The abundances relative to methanol (CH3OH) are plotted in Fig. 5c. The overall chemical composition of Sgr B2(N3) is relatively similar to that of Sgr B2(N5), with at most a factor two of difference between the abundances (relative to CH3OH) of all ten COMs. Sgr B2(N4) shows higher abundances of O- and S-bearing species relative to CH3OH than Sgr B2(N3) and N5, except for NH2CHO, but significantly lower abundances relatives to H2. The chemical composition of Sgr B2(N2) differs significantly from that of the other hot cores. For instance, C2H5CN is about four times more abundant (with respect to CH3OH) in Sgr B2(N2) than toward the other hot cores; in addition, the ratio [C2H5CN]/[C2H3CN] is three times higher. The abundances relative to CH3OH of the O-bearing species CH3OCHO and CH3OCH3 are significantly lower toward Sgr B2(N2) compared to the other sources, but similar to Sgr B2(N3) in terms of abundances relative to H2. Finally, NH2CHO shows an astonishing ratio relative to CH3OH about 15 times larger than toward Sgr B2(N3-N5).
5.2 Model results
In order to interpret the results derived from the observations (Sect. 5.1) we used the astrochemical code MAGICKAL as described in Sect. 4 to compute time-dependent chemical abundances in the envelopes of Sgr B2(N2-N5). In this section we present the results obtained for the standard models N(2-5)-T15-CR1. All abundances refer to fractional abundances with respect to the total hydrogen density (nH = 2n(H2) + n(H)) unless specified otherwise. The effects on the chemical abundances of variations in the minimum dust temperature reached in the cold prestellar phase (that is the quasi-static contraction phase) and the CRIR are discussed in Sects. 6.2 and 6.3, respectively. The final gas-phase fractional abundances calculated for the 11 investigated COMs in all models are given in Table B.1.
 |
Fig. 5 Panel a: column densities of 11 COMs detected toward Sgr B2(N2-N5) (see Table E.2). The error bars show uncertainties on the derived column densities (1σ, see Sect. A). Panel b: chemical abundances relative to H2 of the COMs shown in panel a. The error bars show uncertainties that also include the uncertainty on the H2 column density (1σ, see Sect. 3.1). Panel c: abundances relative to CH3OH of the COMsshown in panel a. The error bars represent 1σ uncertainties on the derived ratios. |
5.2.1 Building up ice mantles
The 1 Myr cold phase prior to the free-fall collapse allows the gas-phase chemistry to quickly convert free atoms into stable simple molecules. Meanwhile, gas-phase material is accreted onto the interstellar dust grains to form ice mantles. The rate of growth of the ice mantles is not linear as a function of time. It is determined by the net rate of deposition of gas-phase material onto the grains and by the degree of surface coverage of bare grains. For the four standard models, N(2-5)-T15-CR1, an ice thickness of one layer is achieved at a time of 6.4 × 103 yr into the simulation (that is t = −0.9936 × 106 yr, see Fig. B.1). The rate of mantle deposition is relatively similar for models N2-T15-CR1, N4-T15-CR1, and N5-T15-CR1, over the whole quasi-static contraction phase. After 1 Myr (that is at t0 = 0), about 110 ice layers have been formed on dust grains for the three models compared to the 161 layers formed in model N3-T15-CR1. This is due to the large densities computed at rstart in the envelope of Sgr B2(N3) during the contraction phase (up to 2 × 106 cm−3, see Fig. F.4a). The accretion of material onto the dust grains is thus more efficient in model N3-T15-CR1, leading to rapid deposition of new ice layers. For all models, the net deposition rate continues to increase until the end of the quasi-static contraction phase, indicating that the depletion of gas-phase material has not reached completion yet.
Figure 6a shows the chemical composition of the grain mantles at each ice layer based on the surface ice that gets incorporated into the mantle. A timescale is indicated such that a time associated to a given ice layer represents the time at which the ice layer was deposited onto the dust grains. The chemical composition within the first 50 ice layers of the grain mantles is similar for the four standard models. Water is clearly the dominant ice constituent for all models, while CO and CO2 are also present in significant quantities (see also Fig. 6b). Given the relatively high dust temperatures (Tmin = 15 K), the slow H-to-H2 conversion on the grains results in high fractional abundances of atomic hydrogen in the gas phase over the whole quasi-static contraction phase (a few 10−3, see Fig. 6c). We find that the surface reaction OH + CH4 → H2O + CH3 is the main mechanism responsible for the formation of water ice, rather than the reaction of OH with atomic or molecular hydrogen expected at lower dust temperatures (T = 10 K, see, e.g., Garrod & Pauly 2011, see also Sect. 6.2). At the beginning of the simulations, the rapid conversion of atomic carbon to CO in the gas phase causes a sharp decline in the abundance of CH4 ices, which in turn affects the abundance of water ice (Figs. 6a and c). Due to the high dust temperature (Tmin = 15 K) the gas-phase CO accreted onto the grains is mobile enough to react with OH radicals to form CO2 + H, limiting the fraction of OH going toward H2O. The abundance of solid-phase CO2 reaches a peak within the first 105 yr of the simulation, representing 60–65% of the water abundance (Fig. 6b). Then, due to the high accretion rate of gas-phase CO onto the dust grains, a rapid switch-over occurs and CO dominates over CO2. H2CO and CH3OH form by the successive hydrogenation of surface CO.
Table 4 gives the chemical composition of the ice mantles at the end of the quasi-static contraction phase for the four standard models. The composition of ices observed in the line of sight of the field star Elias 16 (Whittet et al. 1998)and toward the high-mass protostar W33A (Gibb et al. 2000) are also given for comparison. Models N2-T15-CR1, N4-T15-CR1, and N5-T15-CR1 build up ices with similar chemical composition, also comparable (within a factor ~2) to that of Elias 16. The ice composition in model N3-T15-CR1 differs from that of the other models, in particular with higher abundances of H2CO and CH3OH (see also Fig. 6a). These differences are due to the higher densities computed during the contraction phase at rstart in the more compact inner region of Sgr B2(N3) compared to the other sources. High densities have an impact on the accretion rate of gas-phasespecies onto the dust grains, such that after 1 Myr simple species start to deplete onto dust grains in N3-T15-CR1 (Fig. 6c).
5.2.2 Production of COMs
In this section we investigate the set of chemical reactions that drive the production of the 11 COMs listed in Table E.2. All activation-energy barriers (when there is one) and binding energies may be found in Garrod (2013), Belloche et al. (2017), and references therein. Figure 7 shows the results obtained for the standard models N(2-5)-T15-CR1 under free-fall collapse conditions. Each panel (a and b) shows the evolution of the fractional abundances of a subset of the sample of COMs. Panel a shows the N-bearing species C2H5CN, C2H3CN, CH3CN, NH2CHO, and CH3NCO, as well as CH3SH. Panel b shows the O-bearing species CH3OH, C2H5OH, CH3OCHO, CH3OCH3, and CH3CHO. In each panel the solid lines indicate the gas-phase species while the dotted lines of the same color indicate the solid-phase species, combining both ice-surface and ice-mantle abundances. The calculated fractional abundances are plotted as a function of temperaturein the envelope of the source (in log scale) for easy comparison between all models. A timescale is also indicated at the top of each plot. The figure shows that in most cases, the solid-phase abundances of the investigated COMs directly determine the final gas-phase abundances. This suggests that the gas-phase abundances observed in the warm envelopes ofSgr B2(N2-N5) are dominated by the thermal desorption of the dust-grain ice mantles. In all four models, most COMs are already present on the grains with significant abundances before the warm-up phase (T = 15 K). It is the case for the cyanides C2H5CN and CH3CN, as well as C2H5OH, CH3OH, and CH3SH, indicating that their production mostly relies on the early cold chemistry. Other species still form efficiently on the grains up to ~50 K, in particular the O-bearing species CH3CHO, CH3OCHO, CH3OCH3, NH2CHO, and CH3NCO, suggesting that their production relies on the warm-up stage chemistry.
The peak gas-phase fractional abundances of the ten investigated COMs are given in Table 5 along with the temperatures at which they are achieved for each of the standard models. For comparison,we list also the fractional abundances reached at the end of the simulations (that is T = 400 K). Most species reach their peak abundance right after desorption into the gas phase (except for C2H3CN and CH3NCO), then they quickly reach steady fractional abundances. The O-bearing species CH3OH, C2H5OH, NH2CHO, CH3OCHO, as well as CH3CN, C2H5CN, and CH3SH desorb from the grains at high temperatures (120–147 K). The species which desorb at lower temperatures (via thermal or chemical desorption), or which are formed in the gas phase via ion-molecule reactions, are particularly exposed to gas-phase destruction through photodissociation by CR-induced UV photons or reactions with gas-phase ions.
There islittle gas-phase formation of methanol; it is mostly formed on the grains via successive hydrogenation of the CO accreted from the gas phase:
 (17)
(17)
The high gas-phase fractional abundance of CH3OH at low temperature is mostly due to chemical desorption from the dust grains. Model N3-T15-CR1 shows a modest increase in the gas-phase abundance of CH3OH around T ~ 40 K, caused by the electronic recombination of HC(OH)OCH3+, product of the reaction between protonated methanol (CH3OH2+) and H2CO when the latter is released abundantly into the gas phase.
Ethanol, C2H5OH, is predominantly produced on the grains, mostly via the sequence:
 (18)
(18)
followed by later desorption into the gas phase.
Formamide, NH2CHO, is mainly produced on the grains via the successive hydrogenation of OCN accreted from the gas phase:
 (19)
(19)
The abundance of methyl cyanide, CH3CN, mostly derives from the grain-surface hydrogenation reaction:
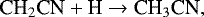 (20)
(20)
where CH2CN is formed via the grain-surface atomic-addition sequence: CN  C2N
C2N  HC2N
HC2N  CH2CN. At low temperatures (T < 50 K), CH3CN is also produced in the gas phase via the electronic recombination of protonated methyl cyanide (CH3CNH+), product of the ion-molecule reaction between CH3+ and HCN.
CH2CN. At low temperatures (T < 50 K), CH3CN is also produced in the gas phase via the electronic recombination of protonated methyl cyanide (CH3CNH+), product of the ion-molecule reaction between CH3+ and HCN.
Methyl formate, CH3OCHO, begins the free-fall collapse phase with modest abundances on the grains. It is formed more efficiently at later times (T ~ 20–30 K), mainly via the grain-surface radical-radical addition reaction:
 (21)
(21)
followed by later desorption into the gas phase. Model N3-T15-CR1 shows a modest increase in the gas-phase abundance of CH3OCHO around 40 K, when (H2CO) is abundantly released into the gas phase and reacts with CH3OH2+ to form HC(OH)OCH3+. Gas-phase CH3OCHO is then produced via the electronic recombination of HC(OH)OCH3+.
Methyl mercaptan, CH3SH, is predominantly formed on the grains via the successive hydrogenation reactions:
 (22)
(22)
During the cold quasi-static contraction phase, CH3SH forms via the successive hydrogenation of surface CS accreted from the gas phase. Above ~20 K, H2CS is accreted onto the grains directly from the gas phase, where it is formed via the electronic recombination of H3CS+, deriving from the ion-molecule reaction S+ + CH4.
Vinyl cyanide, C2H3CN, is formed on dust grains through the successive hydrogenation of HC3N accreted from the gas phase:
 (23)
(23)
Then, as hydrogenation continues on the grain surfaces, C2H3CN is quickly converted to C2H5CN as follows:
 (24)
(24)
Ethyl cyanide, C2H5CN, can thus maintain a steady abundance on the grains, dominating C2H3CN at all times. Only a small fraction of solid-phase C2H3CN contributes to the gas-phase abundance as it is quickly destroyed via a ion-molecule reaction right after desorption. At late times C2H3CN may form inthe gas phase via the reaction:
 (25)
(25)
Due totheir low binding energies to water ices, CH3NCO (3575 K, Belloche et al. 2017), CH3OCH3 (3675 K, Garrod 2013), and CH3CHO (2275 K, Garrod 2013) desorb at low temperatures (that is around 60–80 K). Methyl isocyanate, CH3NCO, starts the free-fall collapse phase with modest abundances on the grains. It is more efficiently produced around 20 K through the radical-addition reaction:
 (26)
(26)
At low temperatures (T < 50 K), CH3NCO may be destroyed on the grains via hydrogenation reactions to form CH3NHCO. In addition, CH3NCO is quickly destroyed via gas-phase ion-molecule reactions right after desorption, leading to very low gas-phase fractional abundances at the end of the simulations (< 10−14 with respect to total hydrogen, for all standard models but N3-T15-CR1). In model N3-T15-CR1, CH3NCO is formed much more abundantly on the grains, mainly because of the high abundance of surface CH3 accreted from the gas phase. Therefore it cannot be destroyed completely once it is released into the gas phase, explaining the higher fractional abundances of gas-phase CH3NCO observed in this model.
Dimethyl ether, CH3OCH3, is mostly formed on the surface of dust grains up to T ~ 20–30 K, through the radical-addition reaction:
 (27)
(27)
In model N3-T15-CR1, the gas-phase fractional abundance of CH3OCH3 increases when CH3OH desorbs from the dust grains around 130 K. This is due to the electronic recombination reaction CH3OCH4+ + e− → CH3OCH3 + H, where CH3OCH4+ is a product of the reaction between CH3OH and CH3OH2+.
Finally, acetaldehyde, CH3CHO, is formed on the grains up to T ~ 30 K, via the surface reactions:
 (28)
(28)
 (29)
(29)
Surface CH3CHO may be destroyed either by reacting with CH3 to form CH4 + CH3CO, or with NH2 to form NH3 + CH3CO. In particular in models N3-T15-CR1 and N4-T15-CR1, only a small fraction of solid-phase CH3CHO contributes to the gas-phase fractional abundance. At lower temperature (T ~ 24 K), surface CH3CHO is released into the gas phase via chemical desorption from the reaction CH2CHO + H. Once in the gas phase, CH3CHO becomes the dominant reaction partner for gas-phase ions, damping ionic abundances and thus limiting the destruction of other gas-phase species. In models N3-T15-CR1 and N4-T15-CR1, CH3CHO is formed directly in the gas phase via the reaction C2H5 + O → CH3CHO + H, when C2H5 desorbs from dust grains around 90 K.
The gas-phase fractional abundances of the 11 investigated COMs obtained at the end of the chemical simulations (that is at T = 400 K) are given for the standard models in Table 5 and plotted in Fig. 8. For each of the 11 COMs the abundances calculated in models N2-T15-CR1 and N5-T15-CR1 are relatively similar. Model N4-T15-CR1 shows significantly lower abundances of CH3CHO, CH3OCHO, and NH2CHO than the other models. Model N3-T15-CR1 significantly differs from the other models. It shows higher abundances of cyanides, and has an astonishing [C2H5CN]/[C2H3CN] ratio >18 times lower than the other models. The final fractional abundance of CH3OH is 2–5 times higher than in the other three models. Finally, N3-T15-CR1 shows an astonishing high abundance of CH3NCO, more than five orders of magnitude higher than for the other models.
 |
Fig. 6 Evolution of the ice-mantle and gas-phase chemistry during the cold quasi-static contraction phase. The results from the standard models N(2-5)-T15-CR1 are displayed from top to bottom. Panel a: calculated fractional ice-mantle composition by ice layer. Panel b: cumulative fractional composition of the ices with respect to water, summed over the grain mantle up to an ice thickness given on the abscissa. Panel c: gas-phase fractional abundances (with respect to total hydrogen) of atomic and simple diatomic species as a function of time with the same time axis as panels a and b to facilitate the comparison. |
Ice mantles composition.
 |
Fig. 7 Calculated fractional abundances for 11 COMs detected toward Sgr B2(N2-N5). Panels a: N-bearing species C2H5CN, C2H3CN, CH3CN, NH2CHO, and CH3NCO, as well as CH3SH. Panels b: O-bearing species CH3OH, C2H5OH, CH3OCHO, CH3OCH3, and CH3CHO. The results for the standard models, N(2-5)-T15-CR1, are shown from top to bottom, as a function of the temperature in the envelope of the sources during the free-fall collapse phase. In each panel the timescale shown at the top is derived from the time-dependent evolution of the temperature in the envelopes of the sources (see Sect. 3.5.2). In each panel, the solid lines show the fractional abundances (with respect to total hydrogen) in the gas phase while the dotted lines show the abundances of the same species on the grains (ice surface+mantle). |
Peak gas-phase abundances and associated temperatures for the standard models.
 |
Fig. 8 Fractional abundances (with respect to total hydrogen) calculated for the standard models at the end of the simulations (that is at T = 400 K). |
6 Discussion
6.1 Physical properties of Sgr B2(N)’s hot cores
In Sect. 3.1 we computed H2 column densities from the dust continuum emission measured toward Sgr B2(N2-N5) in the ALMA continuum emission maps. The results reported in Table 1 show that at a given radius, Sgr B2(N2) has the highest density, lying a factor ~3 above N3 and N4 which have similar densities. The density computed for Sgr B2(N5) lies in between that of the other sources. Given the uncertainties on the calculated densities (Table 1), the differences between the hot cores may be marginal.
The results discussed above slightly differ from our previous analysis of the same ALMA data (Bonfand et al. 2017), where for the H2 column density calculations we assumed a dust mass opacity coefficient (κ100 GHz = 5.9 × 10−3 cm2 g−1) ~1.1 times smaller than the value we use at the same frequency (100 GHz) in this paper (see Fig. F.1). In the case of Sgr B2(N3), which is not detected in the ALMA continuum maps at 3 mm, we used the peak flux density given by Sánchez-Monge et al. (2017; see their Table 1, source AN08) measured at 1.3 mm in an ALMA synthesized beam of 0.4′′. Sánchez-Monge et al. (2017) derived a H2 column density of 4.5 × 1024 cm−2 (see their Table 3) from the integrated flux measured over a source size of 0.59′′ (see Table 1 of Sánchez-Monge et al. 2017). We note that they used a mean molecular weight of μ = 2.33, which corresponds to that of the mean free particle, so that their calculated value has to be divided by ~1.2 to obtain the H2 column density. This gives  = 3.7 × 1024 cm−2, a factor ~4 higher than the value we derived in this paper. The difference is due to the different assumptions made to compute the H2 column density. They assumed a lower dust temperature of 100 K and used a dust mass opacity coefficient (κ230 GHz = 0.011 cm2 g−1) ~1.8 times smaller than our value at the same frequency.
= 3.7 × 1024 cm−2, a factor ~4 higher than the value we derived in this paper. The difference is due to the different assumptions made to compute the H2 column density. They assumed a lower dust temperature of 100 K and used a dust mass opacity coefficient (κ230 GHz = 0.011 cm2 g−1) ~1.8 times smaller than our value at the same frequency.
In Sects. 3.1 and 3.3 we used H2 column densities to compute masses and densities, which are important inputs for the chemical modeling. One must keep in mind that the uncertainties in H2 column densities may have an impact on the chemical model results.
 |
Fig. 9 Panel a: composition of the ice-mantles built up during the cold quasi-static contraction phase prior to the free-fall collapse for the model N2-T10-CR1. Panel b: same as a but for the model N2-T20-CR1. |
6.2 Influence of the minimum dust temperature on the chemistry
As mentioned in Sect. 3.5.1, dust temperature measurements carried out at infrared wavelengths with the Herschel Space Observatory report somewhat higher dust temperatures toward the GC region than other typical regions forming high-mass stars. For instance, Longmore et al. (2012) derived dust temperatures ranging from 19 to 27 K from the center to the edge of the galactic center cloud G0.253+0.016 (also known as “the Brick”). Guzmán et al. (2015) reported measurements of Td = 20–28 K toward Sgr B2, somewhat higher than the 17 K measured for dense cores embedded in the NGC 6334 molecular cloud lying at a distance of 1.3 kpc from the Sun (Chibueze et al. 2014). Recently Belloche et al. (2016) suggested that the low deuteration fractions of COMs observed toward Sgr B2(N) could be explained by either an elemental abundance of deuterium toward the GC region lower than in the solar neighborhood, or higher temperatures during the prestellar phase that would have decreased the efficiency of the deuteration process. Deuteration levels of methanol similar to that of Sgr B2(N) measured toward the aforementioned high-mass star-forming region NGC 6334I located at a distance of ~7 kpc from the GC favor the second hypothesis (Bøgelund et al. 2018). Gas kinetic temperatures ranging from 50 K to more than 100 K were found on the basis of imaging of H2CO transitions with the APEX 12 m telescope (Ao et al. 2013; Ginsburg et al. 2016). Ott et al. (2014) showed that the kinetic temperature distribution of molecular clumps within the region between the supermassive black hole Sgr A* and Sgr B2 peaks at ~38 K based on a survey of NH3 conducted with the Australia Telescope Compact Array (ATCA). In comparison, lower temperatures have been derived from NH3 lines toward several massive clumps outside the GC region (Tg = 10–30 K, Giannetti et al. 2013).
In this section we explore the impact of varying arbitrarily the minimum dust temperature, Tmin (see also Sect. 3.5.1), on the formation of COMs, to account for the high dust temperatures observed toward the GC. Figure 9 shows the chemical composition of the ice mantles built up during the 1-Myr cold contraction phase for the “low temperature” model N2-T10-CR1 (panel a), and the “high temperature” model N2-T20-CR1 (panel b). Significant differences can be seen in the overall chemical composition of the ice mantles compared to the standard model (that is N2-T15-CR1, Fig. 6a, top panel), indicating that the minimum dust temperature adopted in the chemical simulations is of critical importance. The ice mantle formed in the low-temperature model is enriched in CO and depleted in CO2 compared to the standard model. This is due to the less efficient CO-to-CO2 conversion when the dust temperature drops below ~14 K in the low-temperature model. At low temperature, H is converted more efficiently into H2 due to its lower thermal desorption rate, thus decreasing the abundance of gas phase atomic hydrogen compared to the standard model. Surface OH mostly reacts with H2 to form water ice rather than with CO to form CO2. More CO is thus available to form H2CO and CH3OH, enhancing their abundances in the outer ice layers compared to the standard model.
The high-temperature model produces thinner ice mantles than N2-T10/15-CR1, with fewer than 70 ice layers formed on dust grains after 1 Myr. The ice mantles are enriched in carbon dioxide as most surface CO and OH are destroyed to form CO2, decreasing the amount of H2O, H2CO, and CH3OH formed on the grains. The atomic carbon accreted to the grains mostly reacts with surface O2 instead of reacting with atomic hydrogen to form CH, which affects the abundance of CH4. Furthermore, at high temperature reactions involving atomic hydrogen are less efficient because the H coverage of the grains is reduced due to rapid desorption, cutting down the formation of complex species.
The minimum dust temperature adopted in the chemical simulations also has an impact on the abundances of complex species at later times during the free-fall collapse phase, as the investigated COMs have been shown to be mainly produced on the grain surfaces (see Sect. 5.2.2). Figure 10 compares the final gas-phase fractional abundances of the low-,intermediate-, and high-temperature models (see also Figs. B.2–B.5). In most cases, a higher Tmin results in lower fractional abundances. In particular, the O-bearing species CH3OH, CH3NCO, CH3CHO, CH3OCH3, and CH3OCHO are very sensitive to Tmin with, for a given source, fractional abundances lower by more than two orders of magnitude in the high-temperature models compared to the low-temperature model. The fractional abundance of CH3NCO varies by more than four orders of magnitude between the low- and high-temperature models for N2, N3, and N5. The fractional abundance of CH3SH is barely sensitive to changes in Tmin, with at most a factor 3.2 of difference between the low-, intermediate-, and high-temperature models for all sources. This is due to its production mechanism, which relies on gas-phase H2CS which sticks to the dust grains at T ~ 20 K (see Sect. 5.2.2).
A more accurate representation of the dust temperatures in the envelope of Sgr B2(N2-N5), in particular in the outer parts exposed to external UV photons, requires to take into account the dust heating via the interstellar radiation field. The influence of the ISRF strength on the chemical model results is explored in Appendix D. It shows that assuming a radiation field stronger than the standard ISRF value does not improve the agreement between calculated and observed abundances with respect to CH3OH for Sgr B2(N2-N5) (see discussion in Sect. 6.4).
Finally, a more realistic treatment of the grain-surface chemistry would require considering a grain-size distribution rather than single dust-grain radius (0.1 μm) adopted in our simulations. Pauly & Garrod (2016) investigated the effects of a broad grain-size distribution on the ice-surface chemistry by implementing a distribution of five distinct initial grain sizes to their dark cloud models, where the radii of each grain population increase as ice mantles form on the grains. These authors found that when using a uniform dust-grain temperatureacross all grain sizes the surface chemistry does not significantly differ from that of models assuming a single dust-grain radius. However, for chemical models with a more explicit treatment of the grain temperatures, in which Td varies also with the grain-mantle growth of each individual grain-size population, Pauly & Garrod (2016) found that the temperaturedifference plays a significant role in determining the total amount of ice formed and its composition for each grain-size population due to the temperature-sensitive nature of grain-surface reactions.
 |
Fig. 10 Calculated fractional abundances (with respect to total hydrogen) of 11 COMs at the end of the simulations (that is T = 400 K) for the models N2-CR1 (panel a), N3-CR1 (panel b), N4-CR1 (panel c), and N5-CR1 (panel d), assuming a standard CRIR and different Tmin: 10 K in blue, 15 K in purple, and 20 K in red (see Table 3). |
 |
Fig. 11 Composition of the ice mantles built up during the cold quasi-static contraction phase for models N2-T15-CR10 (panel a), N2-T15-CR100 (panel b), and N2-T15-CR1000 (panel c). |
6.3 Influence of the cosmic-ray ionization rate on the chemistry
In this section we explore the impact of varying ζH2 on the formation of COMs. Figure 11 for instance shows the composition of the ice mantles built up during the cold phase prior to the free-fall collapse for Sgr B2(N2), with ζH2 = 10 (N2-T15-CR10), 100
(N2-T15-CR10), 100 (N2-T15-CR100) and 1000
(N2-T15-CR100) and 1000 (N2-T15-CR1000). Panel a shows that the chemical composition of the ices exposed to a CRIR enhanced by a factor of 10 are relatively similar to that obtained for the standard model N2-T15-CR1 (Fig. 7a, top panel). Bigger differences can be seen in the composition of the ice mantles for higher ionization rates. For instance in the models N2-T15-CR100 and N2-T15-CR1000, thicker ice mantles are formed on the grains (up to 153 ice layers for N2-T15-CR100 after 1 Myr, Fig. 11b), than in the low-CRIR models (ζH2 ≤ 10
(N2-T15-CR1000). Panel a shows that the chemical composition of the ices exposed to a CRIR enhanced by a factor of 10 are relatively similar to that obtained for the standard model N2-T15-CR1 (Fig. 7a, top panel). Bigger differences can be seen in the composition of the ice mantles for higher ionization rates. For instance in the models N2-T15-CR100 and N2-T15-CR1000, thicker ice mantles are formed on the grains (up to 153 ice layers for N2-T15-CR100 after 1 Myr, Fig. 11b), than in the low-CRIR models (ζH2 ≤ 10 ). At higher ionization rates, water is still the main ice constituent, but the grain mantles are strongly depleted in CO2 compared to the low-CRIR models, because most surface CO2 is photodissociated via CR-induced UV photons. The abundance of CO in the ice is also diminished because gas-phase CO reacts with He+ before accretion onto dust grains. Gas-phase molecular hydrogen is rapidly dissociated, leading to higher abundances of atomic hydrogen in the gas phase compared to the standard models. Surface reactions involving atomic hydrogen are thus more efficient, as seen in model N2-T15-CR100 which produces ice mantles enriched in CH4 and NH3 compared to the other models. NH3 maintains a fairly stable abundance through the ice layers since the surface NH3 photodissociated to NH2 is quickly hydrogenated to form NH3 again. Finally, the ice mantles in the high CRIR models (ζH2 ≥ 100
). At higher ionization rates, water is still the main ice constituent, but the grain mantles are strongly depleted in CO2 compared to the low-CRIR models, because most surface CO2 is photodissociated via CR-induced UV photons. The abundance of CO in the ice is also diminished because gas-phase CO reacts with He+ before accretion onto dust grains. Gas-phase molecular hydrogen is rapidly dissociated, leading to higher abundances of atomic hydrogen in the gas phase compared to the standard models. Surface reactions involving atomic hydrogen are thus more efficient, as seen in model N2-T15-CR100 which produces ice mantles enriched in CH4 and NH3 compared to the other models. NH3 maintains a fairly stable abundance through the ice layers since the surface NH3 photodissociated to NH2 is quickly hydrogenated to form NH3 again. Finally, the ice mantles in the high CRIR models (ζH2 ≥ 100 ) are significantly depleted in H2CO and CH3OH, which are efficiently destroyed by reacting with surface atomic hydrogen.
) are significantly depleted in H2CO and CH3OH, which are efficiently destroyed by reacting with surface atomic hydrogen.
Besides their impact on the production of ice-mantle constitutents, cosmic rays also play an important role in gas-phase chemical processes, producing the ions that react with gas-phase species leading to their destruction. The results of models N2-T15, N3-T15, N4-T15, and N5-T15 with different CRIRs are plotted in Figs. B.6, B.7, B.8, and B.9, respectively. If we focus for instance on the results obtained for model N2-T15 with different CRIR, Fig. B.6 shows that higher gas-phase fractional abundances of C2H5OH and CH3NCO are obtained at the end of the simulation for a CRIR enhanced by a factor ten compared to the standard value. The final gas-phase fractional abundance of CH3CHO obtained for N2-T15-CR10 is one order of magnitude lower than that of N2-T15-CR1. This is because of reactions with atomic hydrogen destroying CH3CHO on the surface of dust grains. Only a smallfraction of the CH3CHO formed on the grains thus desorbs around 60 K and contributes to its final gas-phase abundance. The CH3CHO present in the gas phase at lower temperatures (that is before thermal desorption) mainly derives from chemical desorption, but once in the gas phase it is quickly destroyed as it reacts with ions.
At higher CRIR, in the model N2-T15-CR100, C2H5OH reaches a final gas-phase fractional abundance of about two orders of magnitude higher than in the standard model. CH3NCO is formed approximately three orders of magnitude more abundantly than in the standard model although it is strongly destroyed by reacting with atomic hydrogen. Its final gas-phase abundance derives from the CR-induced photodissociation of CH3NHCO which desorbs from the grains around T ~ 90 K.
Finally in the model with the highest ionization rate, N2-T15-CR1000, all COMs are affected by cosmic rays (Fig. B.6, bottom panel). In particular, the abundances of COMs with little to no gas-phase formation routes decrease right after desorption from the grain surfaces, leading to low final gas-phase fractional abundances (Fig. 12). This is the case for C2H5OH, CH3OH, CH3OCHO, CH3OCH3, NH2CHO, C2H5CN, and CH3SH, which are all destroyed in the gas phase as they react with one of the most abundant ions, H3O+, produced from water after it desorbs into the gas phase:
 (30)
(30)
The gas-phase abundance of CH3OCH3 decreases by more than three orders of magnitude right after it desorbs from the dust grains. At later times, CH3OCH3 is formed in the gas phase via dissociative recombination of CH3OCH4+, a product of the ion-molecule reaction CH3OH2+ + CH3OH, when CH3OH desorbs from dust grains, around 130 K. The main contribution to the final gas-phase abundance of C2H3CN and CH3CN also comes from gas-phase reactions. C2H3CN is mostly formed via the gas-phase reaction CN + C2H4 → C2H3CN + H, when C2H4 desorbs from dust grains around 70 K, and the dissociative recombination of C2H6CN+. The later reaction is particularly efficient since C2H6CN+ is produced from the ion-molecule reaction H3O+ + C2H5CN. The gas-phase abundance of C2H3CN thus increases as C2H5CN is destroyed. CH3CN reaches its peak gas-phase abundance at early times, around 57 K, after which it is strongly destroyed by ion-molecule reactions. The main contributionto CH3CN’s final gas-phase abundance comes from gas-phase recombination of CH3CNH+, product of the ion-molecule reaction CH3+ + HCN.
Figure 12 shows that the final gas-phase fractional abundances of the 11 investigated COMs are very sensitive to the CRIR for Sgr B2(N2-N5). For instance, the abundances of cyanides rise as the CRIR increases up to 100 . For higher ionization rates (
. For higher ionization rates ( ≥ 500
≥ 500 ), the final gas-phase abundance of C2H5CN decreases significantly, leading to [C2H5CN]/[C2H3CN] < 1 in all models (see also Fig. 16). The final fractional abundances calculated by models N3-T15 and N4-T15 are strongly diminished at high CRIR (1000
), the final gas-phase abundance of C2H5CN decreases significantly, leading to [C2H5CN]/[C2H3CN] < 1 in all models (see also Fig. 16). The final fractional abundances calculated by models N3-T15 and N4-T15 are strongly diminished at high CRIR (1000 ) compared to the low ionization-rate models, except for CH3CHO. Model N2-T15-CR1000 shows significantly higher fractional abundances of C2H5OH, CH3CHO, and CH3NCO compared tothe standard model N2-T15-CR1. The impact of varying the CRIR on the calculated fractional abundances depends on the source, suggesting that the chemical differences discussed here may be exacerbated by the different physical properties of the cores.
) compared to the low ionization-rate models, except for CH3CHO. Model N2-T15-CR1000 shows significantly higher fractional abundances of C2H5OH, CH3CHO, and CH3NCO compared tothe standard model N2-T15-CR1. The impact of varying the CRIR on the calculated fractional abundances depends on the source, suggesting that the chemical differences discussed here may be exacerbated by the different physical properties of the cores.
 |
Fig. 12 Calculated gas-phase fractional abundances (with respect to total hydrogen) of 11 COMs obtained at the end of the simulations for model N2-T15 (panel a), N3-T15 (panel b), N4-T15 (panel c), and N5-T15 (panel d), with different CRIR values as shown in Table 3. Species with fractional abundances lower than 10−15 are not visible in the histograms. |
6.4 Comparison with observations
6.4.1 Main trends and uncertainties
The gas-phase fractional abundances obtained at T = 150 K (which corresponds to T0, see Sect. 3.2) for the 11 investigated COMs in all models are given in Table B.2. The results of all chemical models are also plotted in Fig. 13 compared to the observed abundances with respect to CH3OH. It shows that in most cases the chemical models tend to underestimate the observed abundances. In particular, this is the case for CH3OCHO, for which the calculated abundances are lower than the observed ones toward all four sources. The abundance of CH3NCO with respect to CH3OH is also underestimated by all models, by at least two orders of magnitude compared to the observed abundances. In Sect. 5.2.2 we have seen that solid-phase CH3NCO desorbs from the grains around 70 K, however, the measured rotational temperatures toward Sgr B2(N2-N5) are higher than 140 K (Sect. E.2). This suggests that some important chemical reactions involved in the production of CH3NCO may be missing in the chemical network (see, e.g., Quénard et al. 2018), or that the binding energy adopted for CH3NCO in our chemical models (3575 K, Belloche et al. 2017) is underestimated (see Belloche et al. 2019, for models computed with a higher binding energy). For this reason we ignored CH3NCO in the rest of the discussion.
In Fig. 13 no error bars are plotted on the model results although it has been shown that calculated chemical abundances may be affected by rate coefficient uncertainties (see, e.g., Wakelam et al. 2005). Given the large number of parameters in the chemical code, a full analysis taking into account both observational and theoretical uncertainties (see, e.g., Wakelam et al. 2006) would be too difficult and is not attempted here. Besides, additional uncertainties affecting the model results derive from the lack of experimental and theoretical data on grain-surface processes. For instance, Iqbal et al. (2018) found that the abundances of both gas-phase and surface species calculated under typical dark cloud conditions are affected by large errors due to the uncertainties in the diffusion energy of surface species, in particular for the molecules predominantly formed at the grain surface like CH3OH. Enrique-Romero et al. (2016) presented quantum chemical computations showing that grain-surface radical-radical addition reactions do not necessarily lead to the formation of complex species because these radicals are trapped by the water-ice molecules with an orientation that favors other two-product reactions. This suggests that gas-phase reactions may play a more important role in the formation of COMs than currently assumed in chemical models. Recently Skouteris et al. (2018) computed rate coefficients for two gas-phase ion-molecule reactions proposed as main formation route for ceCH3OCH3: CH3OH + CH3OH2+ → (CH3)2OH+ + H2O followed by the reaction of (CH3)2OH+ with NH3 to form CH3OCH3 + NH4+. The latter reaction, not included in our chemical network, could help in improving the agreement between the calculated and observed [CH3OCH3]/[CH3OH] ratios, which differ by at least one order of magnitude in our models for N3-N5 (see Fig. 13).
6.4.2 Constraining the physical parameters Tmin and ζH2
We used the method presented by Garrod et al. (2007) to evaluate the level of confidence of each model with respect to the observations in order to determine which set of physical parameters (Tmin and CRIR, that is ζH2) best characterizes Sgr B2(N)’s hot cores (see Appendix C for details about the method). We draw our attention first to the overall abundances of COMs with respect to H2, and then examine in more detail the influence of Tmin and CRIR on the chemical composition itself, that is the COM abundances relative to CH3OH or CH3CN.
Figure 14 shows the confidence levels for the ten investigated COMs (excluding CH3NCO) relative to H2, for Sgr B2(N2-N5) taken individually and for all sources taken together. Panels a, b, and c show the confidence levels for all molecules, only the O-bearing molecules, and only the cyanides, respectively. The confidence level matrices differ from one source to the other, maybe reflecting the limits of our strong assumption that all sources share the same accretion history. Given that all sources should have been exposed to the same cosmic-ray flux and probably shared a similar thermal history during the prestellar phase, we focus our attention on the matrices corresponding to all sources taken together. The cyanides appear to be much more sensitive to Tmin and CRIR than the O-bearing species. The cyanides constrain the CRIR value to be about 50 times the standard one, and the minimum temperature to be below 20 K. The best confidence levels for the O-bearing species are also obtained for these values, but the constraints are less sharp.
Given that a model with Tmin = 20 K still gives acceptable results for the O-bearing species, we ran additional simulations with Tmin = 25 and 28 K for N2, with ζH2 = 50 (see Fig. F.9a). Ignoring the cyanides, we obtained confidence levels of about 10 and 5% for the models N2-T25-CR50 and N2-T28-CR50, respectively. These values are much lower than the 23% obtained for N2-T20-CR50. This results from the high dust temperatures (Tmin ≥ 25 K) preventing gas-phase atoms and simple molecular species such as CO to stick to the grains, damping the formation of ice mantles and thus the production of complex species. We expect the models of N3-N5 to behave in the same way and conclude that the COM abundances relative to H2 in N2-N5 certainly exclude Tmin > 20 K.
(see Fig. F.9a). Ignoring the cyanides, we obtained confidence levels of about 10 and 5% for the models N2-T25-CR50 and N2-T28-CR50, respectively. These values are much lower than the 23% obtained for N2-T20-CR50. This results from the high dust temperatures (Tmin ≥ 25 K) preventing gas-phase atoms and simple molecular species such as CO to stick to the grains, damping the formation of ice mantles and thus the production of complex species. We expect the models of N3-N5 to behave in the same way and conclude that the COM abundances relative to H2 in N2-N5 certainly exclude Tmin > 20 K.
We now focus on the COM chemical composition itself and show in Fig. 15 the matrices of confidence levels computed for nine COMs relative to CH3OH (panel a), the O-bearing molecules relative to CH3OH (panel b), and the cyanides relative to CH3CN (panel c). This refinement reveals that the O-bearing COM chemical composition relative to CH3OH is sensitive to the CRIRvalue, with the best-fit value being 50 times the standard value, in agreement with the constraints obtained from the cyanide abundances relative to H2 (see Fig. 14). A minimum temperature below 20 K seems to be favored as well. The cyanide chemical composition with respect to CH3CN is less sensitive to the two investigated parameters (bottom panel of Fig. 15c). However, a more detailed investigation reveals that the abundance ratio of C2H5CN to C2H3CN, two species that are chemically linked (see Sect. 5.2.2), is sensitive to the CRIR. Figure 16 shows that this ratio decreases as the CRIR increases in the four sources Sgr B2(N2–N5). The observed ratios are best reproduced by the models with 50 ≤ ζH2 ≤100
≤ ζH2 ≤100 , due to the increase in the gas-phase abundance of C2H3CN at late times (that is high temperatures) in these models. This behavior is consistent with what we observe, in particular toward Sgr B2(N2) where the rotational temperature derived for C2H3CN is higher than that of C2H5CN. The flat gas-phase abundance profile of C2H3CN at T > 40 K in the standard models with lower CRIR (Fig. 7) would imply that it traces more extended regions than C2H5CN, which would be inconsistent with what is observed in Sgr B2(N2).
, due to the increase in the gas-phase abundance of C2H3CN at late times (that is high temperatures) in these models. This behavior is consistent with what we observe, in particular toward Sgr B2(N2) where the rotational temperature derived for C2H3CN is higher than that of C2H5CN. The flat gas-phase abundance profile of C2H3CN at T > 40 K in the standard models with lower CRIR (Fig. 7) would imply that it traces more extended regions than C2H5CN, which would be inconsistent with what is observed in Sgr B2(N2).
Our analysis above shows that the chemical models with a CRIR enhanced by a factor 50 compared to the standard value best reproduce the observations for the four hot cores taken together. However, one must keep in mind that for simplicity our models assume that cosmic rays are not attenuated in the envelope of the sources, although the large visual extinctions of Sgr B2(N2-N5) (see Figs. F.4b and F.7b) may actually lead to attenuation of the cosmic-ray flux. Neufeld & Wolfire (2017) showed, based on H2 and H3+ column densities measured toward diffuse clouds in the galactic disk, that the CRIR decreases with increasing H2 column density with a best-fit dependence scaling as N(H2)−a with a = 0.92 ± 0.32 for N(H2) ~ 1020 – 1022 cm−2. This implies that the cosmic-ray flux is attenuated by a factor ~70–600 from the diffuse regions with N(H2) = 1021 cm−2 to the dense gas with N(H2) = 1023–1024 cm−2. The attenuation of the cosmic-ray flux might have a significant impact on the chemical model results. For instance, Rimmer et al. (2012) showed that a column-density-dependent CRIR improves the agreement between chemical model predictions and observationsfor the Horsehead nebula, compared to a standard model with a constant CRIR. For a more sophisticated treatment of the cosmic-ray driven chemistry in hot core models including cosmic-ray attenuation see, Willis et al. (in prep.).
Moreover, our models do not take into account direct cosmic-ray bombardment of dust-grain ice mantles although laboratory experiments showed that it can trigger a rich chemistry that may lead to the formation of more complex species even at very low temperatures (Hudson & Moore 2001; Rothard et al. 2017). Recently, Shingledecker et al. (2018) used chemical models to investigate the effect of direct cosmic-ray collisions with dust grains on the solid-phase chemistry, including the formation of suprathermal species in the ices from collision with energetic particles. For instance, for a standard CRIR (10−17 s−1), they found that the abundance of CH3OCHO, which is systematically underproduced in all our models (Fig. 13), is significantly enhanced in the gas phase, as well as on the grains compared to the standard chemical model (that is without cosmic-ray driven reactions).
As reported above, our models firmly exclude minimum dust temperatures of 25 K or higher during the prestellar phase of N2-N5. Such high temperatures would prevent the production of COMs at the level observed in these sources. Our models show that a value of 15 K, higher than the low values used in previous studies (≤10 K, see, e.g., Müller et al. 2016; Belloche et al. 2017; Garrod et al. 2017), still leads to an efficient production of COMs roughly consistent with the observations, while for 20 K signs of disagreement emerge between model and observations, especially for the cyanide abundances relative to H2 and the O-bearing COM chemical composition relative to CH3OH. A more accurate treatment of the dust temperatures in the envelope of Sgr B2(N2-N5) for different values of the ISRF does not modify the results much compared to our simple parametrization with an artificially-set minimum temperature (see Table D.1). A value of 15 K is close to the lowest dust temperatures measured in the GC region (19–20 K, see Sect. 6.2). It could even be that models with Tmin =17–18 K produce COMs in amounts that are still consistent with the abundances measured in Sgr B2(N)’s hot cores. In addition, the coldest dust grains in the GC region may be masked by warmer outer layers and thus have been missed by Herschel because of its limited angular resolution. Therefore, it is likely that the constraint we derived on Tmin from the COM abundances is fully consistent with the thermal properties of the GC region.
 |
Fig. 13 From top to bottom: abundances of ten COMs with respect to CH3OH calculated atT = 150 K by the models N2-N5, with different Tmin. In each panel the different symbols indicate the abundances calculated with different CRIR values. The horizontal black lines show the observed abundances relative to CH3OH. The gray boxes represent the 1σ uncertainties. Arrows indicate upper limits. The abundances relative to CH3OH lower than 10−9 are not visible in the plots. |
 |
Fig. 14 Panel a: matrice of confidence levels of the models with respect to the observed abundances of ten COMs relative to H2. The first four panels in this column show, from top to bottom, the results for Sgr B2(N2), N3, N4, and N5, respectively. Bottom panel: average matrice for all four hot cores taken together. Panel b: same as (a) but only for the O-bearing species CH3OH, CH3OCHO, CH3OCH3, CH3CHO, C2H5OH, and NH2CHO. Panel c: same as (a) but only for the cyanides CH3CN, C2H5CN, and C2H3CN. |
 |
Fig. 15 Panel a: matrice of confidence levels of the models with respect to the observed abundances of nine COMs relative to CH3OH. The first four panels in this column show, from top to bottom, the results for Sgr B2(N2), N3, N4, and N5, respectively. The bottom panel shows the average matrice for all four hot cores taken together. Panel b: same as (a) but for the abundances relative to CH3OH of the O-bearing species CH3OCHO, CH3OCH3, CH3CHO, C2H5OH, and NH2CHO only. Panel c: same as (a) but for the abundances relative to CH3CN of the cyanides C2H5CN and C2H3CN only. |
6.5 Chemical differentiation between N- and O-bearing complex molecules
Chemical differentiation between O- and N-bearing species has been observed toward several high-mass star-forming cores (Blake et al. 1987; Wright et al. 1992; Wyrowski et al. 1999; Beuther et al. 2005; Allen et al. 2017). Recently, Csengeri et al. (2018) investigated the young high-mass star-forming region G328.2551–0.5321 where CH3OH and other O-bearing species show two distinct bright emission peaks spatially offset from the peak of the cyanides (see also Csengeri et al. 2019). The authors suggested that in this source, CH3OH traces the accretion shocks resulting from the interaction between the collapsing envelope and the accretion disk, while the cyanide emission may trace the more compact hot region radiatively heated by the protostar. In this scenario, the O-bearing COM emission detected in the envelope of G328.2551–0.5321 arises from accretion shocks rather than from the region radiatively heated by the protostar itself. If such a mechanism is at play in Sgr B2(N) at scales smaller than the beam of the EMoCA survey, then infering the luminosity of the protostars from the rotational temperature measured at the radius of the COM emission as we did in Sect. 3.3 would be wrong. The thermal history derived for Sgr B2(N2-N5) (see Sect. 3.5.2) would then be incorrect, and this could have a significant impact on the results of our chemical modeling. Observations at higher angular resolution that are attained in the ReMoCA survey (Belloche et al. 2019) are needed to investigate whether a chemical differentiation between N- and O-bearing species occurs in Sgr B2(N)’s hot cores.
6.6 Limitations on the physical models of Sgr B2(N2-N5)
In Sect. 3.4 we have estimated the age, tsource, of each hot core based on the estimated current luminosities (Sect. 3.3). To do so, we used the relation L (t) obtained from RMHD simulations of high-mass star formation (Peters et al. 2011, see also Sect. 3.4), combined with the mass-luminosity relation given by Hosokawa & Omukai (2009). The estimated tsource values are unlikely to be accurate because our analysis assumes that the evolution of the accretion rate, Ṁ (t), is the same for all sources, although the density measured at a given radius toward Sgr B2(N2) is a factor 3.2, 3.5, and 2.0 higher than that of N3, N4, and N5, respectively (Fig. F.7b). In addition, the simulations of Peters et al. (2011) were set up for a molecular cloud with a central core gas mass density of ρg = 1.27 × 10−20 g cm−3 within a radius of 0.5 pc, which is about 10–40 times lower than the values we derive for Sgr B2(N2-N5) at the same radius (Fig. F.7b). Using the mass-luminosity relation provided by Hosokawa & Omukai (2009) for a constant accretion rate of 10−4 M⊙ yr−1, the final mass of ~30 M⊙ obtained using the model from Peters et al. (2011) leads to a final luminosity of ~105L⊙, significantly lower than the values we derive for Sgr B2(N2-N5) (Sect. 3.3).
Our simplified treatment, in which we assumed that the accretion rate does not drop below 10−4 M⊙ yr−1 to form more massive and more luminous objects (Sect. 3.4), results in significant differences in the time evolution of Sgr B2(N3)’s physical parameters (nH, Av, and T) compared to the other three sources. Given its lower luminosity, N3 is apparently younger than the other sources (see Table 1). In the framework of our model, this results in a faster increase of the density and temperature along the trajectory of the modeled parcel of gas during the free-fall collapse phase of N3. Figure F.9 shows that our best models (that is with ζH2 = 50 ) better reproduce the chemical abundances (with respect to H2) of C2H5OH and CH3OH in Sgr B2(N3) compared to the other sources. However, the modeled abundances of CH3OCHO and CH3OCH3 are 2–3 orders of magnitude lower than the abundances measured toward N3. This might suggest that the relations Ṁ (t), M (t), and L (t) we derived in Sect. 3.4 do not represent accurately the physical evolution of Sgr B2(N2-N5). Furthermore, in our previous analysis of Sgr B2(N)’s hot cores (Bonfand et al. 2017), we proposed a tentative evolutionary sequence in which N4 appears younger than N3, based on the molecular outflow signature detected toward N3, while N4 does not show any evidence of outflow yet. This is in contradiction with the present analysis in which we find that N3 is the youngest of the four investigated hot cores. This is another indication that the short evolution timescale we obtain here for N3 may not represent well the physical evolution of the source. However, the origin of some wing emission seen in the spectrum of N4 is not understood (see discussion in Sect. 3.7 in Bonfand et al. 2017) and a search for a bipolar outflow in N4 should be carried out with more robust outflow tracers, such as CO, whose J = 1–0 transition is not covered by the EMoCA survey.
) better reproduce the chemical abundances (with respect to H2) of C2H5OH and CH3OH in Sgr B2(N3) compared to the other sources. However, the modeled abundances of CH3OCHO and CH3OCH3 are 2–3 orders of magnitude lower than the abundances measured toward N3. This might suggest that the relations Ṁ (t), M (t), and L (t) we derived in Sect. 3.4 do not represent accurately the physical evolution of Sgr B2(N2-N5). Furthermore, in our previous analysis of Sgr B2(N)’s hot cores (Bonfand et al. 2017), we proposed a tentative evolutionary sequence in which N4 appears younger than N3, based on the molecular outflow signature detected toward N3, while N4 does not show any evidence of outflow yet. This is in contradiction with the present analysis in which we find that N3 is the youngest of the four investigated hot cores. This is another indication that the short evolution timescale we obtain here for N3 may not represent well the physical evolution of the source. However, the origin of some wing emission seen in the spectrum of N4 is not understood (see discussion in Sect. 3.7 in Bonfand et al. 2017) and a search for a bipolar outflow in N4 should be carried out with more robust outflow tracers, such as CO, whose J = 1–0 transition is not covered by the EMoCA survey.
We also point out that the ages we obtain for Sgr B2(N2), N4, and N5 in Sect. 3.4 are about four times longerthan the hot core lifetime we estimated in our previous analysis of Sgr B2(N)’s hot core population (~6 × 104 yr, Bonfand et al. 2017)on the basis of a very simple statistical argument involving the number of hot coresand UCHII regions detected in the same area and assuming a lifetime of ~105 yr for the UCHII phase (Peters et al. 2010). This might suggest that the accretion rate, Ṁ (t), of these sources is/was actually higher than what we have assumed here.
In orderto better represent the extreme physical conditions (densities/masses, luminosities) of Sgr B2(N)’s hot cores and give an accurate estimate of their age, RMHD simulations treating specifically their different physical properties will be needed. In addition a more self-consistent treatment of the accretion rate, mass, and luminosity evolution (that is, taking into account the time-dependent evolution of the accretion rate to derive the mass-luminosity relation) is also required.
 |
Fig. 16 Calculated fractional abundances of C2H5CN with respect to C2H3CN as a function of the CRIR. In each panel, the different symbols indicate the abundances calculated at T = 150 K for different minimum dust temperatures and the horizontal black line shows the observed ratio. Uncertainties (1σ) are shown in gray. The [C2H5CN]/[C2H3CN] ratios obtained for models N3-CR500 ad N3-CR1000 (<10−2) are not displayed. |
7 Conclusions
We analyzed the results of the 3 mm imaging line survey EMoCA conducted with ALMA in its cycles 0 and 1 to characterize the hot core population embedded in Sgr B2(N). We derived the chemical composition of the three hot cores Sgr B2(N3-N5) focusing on 11 COMs. We investigated the time-dependent evolution of the protostellar properties and we derived the evolution of density, temperature, and visual extinction in the envelopes of Sgr B2(N2-N5). We used the astrochemical code MAGICKAL to simulate the time-dependent chemical evolution of the sources based on their physical evolution. We investigated the impact of the cosmic rays and the minimum dust temperature reached during the cold prestellar phase on the chemical abundances calculated by the models. We compared the results to the observations to constrain the physical parameters which best represent the environmental conditions characterizing Sgr B2(N) and the GC region. Our main results are the following:
- 1.
Sgr B2(N3) and N5 share a similar chemical composition relative to methanol. The chemical composition of Sgr B2(N2) differs significantly from the other hot cores Sgr B2(N3-N5).
- 2.
We derived gas densities of 1.4 × 107 cm−3 toward Sgr B2(N2) at a radius of 6010 au (~0.03pc), while the values derived for N3, N4, and N5 at the same radius are a factor 3.2, 3.5, and 2.0 lower, respectively.
- 3.
On the basis of the rotational temperature derived for the COMs and using the results of RMHD simulations of high-mass star formation, the current luminosities of the hot cores are estimated to be 2.6 × 105 L⊙, 4.5 × 104 L⊙, 3.9 × 105 L⊙, 2.8 × 105 L⊙ for Sgr B2(N2), N3, N4, and N5, respectively. These results hold only if our assumption that the COM emission arises from the region radiatively heated by the protostar is valid.
- 4.
The production of the cyanides C2H5CN and CH3CN as well as CH3OH and C2H5OH mostly relies on the early cold grain-surface chemistry (Td ≤ 15 K), while the O-bearing species CH3CHO, CH3OCHO, CH3OCH3 are predominantly formed during the warm-up phase of the protostellar evolution.
- 5.
COMs form efficiently on grains during the prestellar phase of Sgr B2(N2-N5) with minimum dust temperatures as high as 15 K. Minimum dust temperatures ≥25 K are firmly excluded by our chemical models.
- 6.
The cosmic-ray ionization rate adopted in the chemical simulations is critical, in particular during the warm-up stage where cosmic rays may rapidly destroy COMs once they are released into the gas phase. The best match between chemical models and observations is obtained for ζH2 = 7 × 10−16 s−1, that is a CRIR enhanced by a factor 50 compared to the solar neighborhood value. This is somewhat lower than extreme values expected toward the diffuse medium in the GC region (1 – 11 × 10−14 s−1). This difference may reflect the attenuation of cosmic rays in denser gas.
The chemical composition calculated by our models for Sgr B2(N)’s hot cores strongly depends on their history since the initial stages in the prestellar phase. Our strong assumption about the accretion history being the same for all sources implies a much shorter timescale for Sgr B2(N3) which has a significant impact on its calculated chemical composition and results in a worse agreement with the observations. Furthermore, our model in which the three other hot cores, N2, N4, and N5 are by far older than N3 is inconsistent with the tentative evolutionary sequence suggested inour previous analysis of Sgr B2(N)’s hot cores based on their association with class II methanol masers, outflows, and UCHII regions (Bonfand et al. 2017). This emphasizes the need for RMHD simulations tailored to each hot core in order to have a more realistic description of their history and improve the reliability of the chemical model results.
Acknowledgements
We would like to thank the anonymous referee for his/her comments that helped to improve the paper. We thank Takeshi Hosokawa for providing us the results of their star-formation models in electronic form. MB thanks the University of Virginia for hosting her as a visiting student. Part of this work has been carried out within the Collaborative Research Centre 956, sub-project B3, funded by the Deutsche Forschungsgemeinschaft (DFG) – project ID 184018867. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00017.S, ADS/JAO.ALMA#2012.1.00012.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The interferometric data are available in the ALMA archive at https://almascience.eso.org/aq/.
Appendix A Uncertainties on the molecular column densities
The column densities estimated in Sect. 5.1 for Sgr B2(N3-N5) (see also Table. E.2) are based on simple assumptions, such as a single excitation temperature to characterize all transitions from a given molecule under the LTE approximation. In addition, because the hot core emission toward Sgr B2(N3-N5) is resolved in our data for only a few species, especially toward Sgr B2(N3) for which transitions from only two species could be used to derive the source size (Bonfand et al. 2017), we assume for each of these three sources that all molecules are emitted from the same region characterized by a single size. This may not be true as it is shown in Sect. 5.2.2 that all investigated COMs do not desorb from the dust grains at the same temperature in the chemical models, suggesting that they may trace different regions.
In orderto estimate the uncertainties on the column densities we varied for each species detected toward Sgr B2(N3-N5) the emission size and rotational temperature within the uncertainties given by the 2D Gaussian fits to the integrated intensity maps and population diagrams, respectively. Comparing the column densities derived with our best-fit synthetic spectra (Table E.2) with those obtained varying temperature and source size, we find that column densities vary at most by a factor four. In the case of Sgr B2(N2) we simply assume uncertainties of 30% on the molecular column densities of all investigated species.
Appendix B Results of the chemical simulations
Figure. B.1 shows the growth of the dust-grain ice mantles calculated by the chemical models N(2-5)-T15-CR1 during the quasi-static contraction phase prior to the free-fall collapse. Figures B.2–B.5 and B.6–B.9 show the impact on the chemical model results for Sgr B2(N2-N5) of varying the minimum dust temperature and the CRIR, respectively. Tables B.1–B.2 give the results of all the chemical models obtained at the end of the simulations (Tmax = 400 K) and at T0 = 150 K, respectively.
 |
Fig. B.1 Growth of the dust-grain ice mantles over time during the quasi-static contraction phase for the standard models N(2-5)-T15-CR1. |
 |
Fig. B.2 Calculated fractional abundances of 11 COMs for models N2-T10-CR1 (top panels) and N2-T20-CR1 (bottom panels), plotted as a function of temperature in the envelope of Sgr B2(N2) during the free-fall collapse phase. In each panel the timescale shown at the top is derived from the time-dependent evolution of the temperature along the trajectory of the infalling parcel of gas (see Sect. 3.5.2). In each panel, the solid lines show the fractional abundances (with respect to total hydrogen) in the gas phase while the dotted lines show the abundances of the same species on the grains (ice-surface+mantle). |
 |
Fig. B.6 Same as B.2 but for models N2-T15-CR10 (top panels), N2-T15-CR100 (middle panels), and N2-T15-CR1000 (bottom panels). |
 |
Fig. B.7 Same as B.2 but for models N3-T15-CR10 (top panels), N3-T15-CR100 (middle panels), and N3-T15-CR1000 (bottom panels). |
 |
Fig. B.8 Same as B.2 but for models N4-T15-CR10 (top panels), N4-T15-CR100 (middle panels), and N4-T15-CR1000 (bottom panels). |
 |
Fig. B.9 Same as B.2 but for models N5-T15-CR10 (top panels), N5-T15-CR100 (middle panels), and N5-T15-CR1000 (bottom panels). |
Final gas-phase fractional abundances calculated by the chemical models.
Gas-phase fractional abundances at T = 150 K.
Appendix C Confidence level of the models with respect to the observations
Mean confidence level (%) for ten COMs with respect to H2.
In order todetermine which set of physical parameters (Tmin and CRIR) best characterizes Sgr B2(N)’s hot cores (see Sect. 6.4.2), we evaluate the success of each model in reproducing the observations using the method presented by Garrod et al. (2007). For each model, we compute a level of confidence, κi, in the agreement between calculated and observed abundances (relative to H2, CH3OH, or CH3CN). For each calculated abundance ratio, the level of confidence is given by:
 (C.1)
(C.1)
which computes the logarithmic distance of disagreement between the calculated abundance ratio (Rmodel, i) and the observed one (Robs, i). We define the standard deviation σ = 1 such that one standard deviation corresponds to one order of magnitude lower/higher than the observed abundance ratio. erfc is the complementary error function (erfc = 1−erf) such that κi ranges between 0 and 1. For instance, a calculated abundance ratio lying one order of magnitude lower/higher than the observed one has a confidence level κi = 31.7% (and κi = 4.6% for two orders of magnitude etc.). For each model we take the mean of the confidence levels obtained for the molecules in the sample to define the overall confidence level of the model with respect to the observations. The results are given in Tables C.1–C.6.
Mean confidence level (%) for O-bearing species with respect to H2.
Mean confidence level (%) for cyanides with respect to H2.
Mean confidence level (%) for nine COMs with respect to CH3OH.
Mean confidence level (%) for O-bearing species with respect to CH3OH.
Mean confidence level (%) for cyanides with respect to CH3CN.
Appendix D Influenceof the external radiation field on the chemistry
Investigations carried out on the extreme environmental conditions characterizing the GC region suggest that the ambient radiation field may be enhanced by a factor ~500–1000 in the innerGalaxy (Lis et al. 2001; Clark et al. 2013), compared to the standard ISRF value (1 G0) used in our simulations. A stronger ISRF may not have a big impact on the warm chemistry during the free-fall collapse phase, because external UV photons are rapidly absorbed as the visual extinction increases. However, it may be more critical during the preceding low-density phase, where dust grains are not efficiently shielded against external radiation. Recently, Hocuk (2017) derived a parametric expression of the dust temperature scalable with the interstellar radiation field strength. Based on their analysis we scale the dust temperature expression of Garrod & Pauly (2011) (see Sect. 3.5.1) as follows:  =
=  , where χUV represents the strength of the UV field in units of the standard Draine field. In order to explore the impact of a stronger radiation field on the production of COMs, we run three additional chemical models, N2-UV100, N2-UV500, and N2-UV1000, with χUV= 100 G0, 500 G0, and 1000 G0, respectively.No minimum threshold is fixed for the dust temperatures, which go as low as ~14, 17, and 19 K in models N2-UV100, N2-UV500, and N2-UV1000, respectively. The gas temperature, Tg, is held constant at 15 K during the whole quasi-static contraction phase. We adopt
, where χUV represents the strength of the UV field in units of the standard Draine field. In order to explore the impact of a stronger radiation field on the production of COMs, we run three additional chemical models, N2-UV100, N2-UV500, and N2-UV1000, with χUV= 100 G0, 500 G0, and 1000 G0, respectively.No minimum threshold is fixed for the dust temperatures, which go as low as ~14, 17, and 19 K in models N2-UV100, N2-UV500, and N2-UV1000, respectively. The gas temperature, Tg, is held constant at 15 K during the whole quasi-static contraction phase. We adopt  = 6.5 × 10−16 s−1 as found to be the CRIR that best reproduces the observations toward Sgr B2(N2-N5) (see Sect. 6.4.2). Figure D.1 compares the calculated gas-phase fractional abundances of ten COMs relative to CH3OH for the models with strong UV fields to the observed abundances. The results of model N2-CR50-UV1, with a standard radiation field and a minimum dust temperature Tmin = 15 K, are also shown for comparison. It shows that stronger UV fields increase the discrepancy between the calculated and observed abundances of cyanides with respect to CH3OH, while the abundances of NH2CHO, CH3CHO, and C2H5OH relative to CH3OH are only slightly affected by the UV field strength.
= 6.5 × 10−16 s−1 as found to be the CRIR that best reproduces the observations toward Sgr B2(N2-N5) (see Sect. 6.4.2). Figure D.1 compares the calculated gas-phase fractional abundances of ten COMs relative to CH3OH for the models with strong UV fields to the observed abundances. The results of model N2-CR50-UV1, with a standard radiation field and a minimum dust temperature Tmin = 15 K, are also shown for comparison. It shows that stronger UV fields increase the discrepancy between the calculated and observed abundances of cyanides with respect to CH3OH, while the abundances of NH2CHO, CH3CHO, and C2H5OH relative to CH3OH are only slightly affected by the UV field strength.
Table D.1 gives the mean confidence level of the models with the observations for different χUV. It shows that the highest confidence level for the abundances of nine COMs (excluding CH3NCO) with respect to CH3OH is obtained with the model assuming a standard ISRF (1 G0). The confidence levels drop significantly for models with higher χUV. The opposite behavior is obtained when computing confidence levels with only the cyanides C2H3CN and C2H5CN with respectto CH3CN (that is the agreement with observations increases with the UV field strength). Finally, all models have similar confidence levels when computed based only on the O-bearing species CH3OCHO, CH3OCH3, CH3CHO, C2H5OH, and NH2CHO. This does not allow us to conclude strictly on which interstellar radiation field better characterizes Sgr B2(N). This is consistent with the results we obtain by simply parametrizing the dust temperature profile with an artificially-set minimum temperature (see Sect. 6.4.2).
As pointed out by Hocuk (2017), the dust temperature expression of Garrod & Pauly (2011) results in higher temperatures at low visual extinctions than the values computed using the
parametric expression of Hocuk (2017; see their Fig. 7). For comparison, we plot in Fig. D.1 the fractional abundances with respect to CH3OH calculated by model N2-CR50-Tdhoc-UV100, which uses the dust temperature expression given by Hocuk (2017; see their Eq. (8)). Figure D.1 shows that the expression used to compute the dust temperaturedoes not have a strong impact on the production of COMs, as there is at most a factor ~1.6 of difference in the abundances with respectto CH3OH calculated by models N2-CR50-Tdhoc-UV100 and N2-CR50-UV100.
 |
Fig. D.1 Chemical abundances with respect to CH3OH of ten COMscalculated at T = 150 K by the models N2-CR50. The different symbols indicate the abundances calculated with different χUV. Model Tdhoc-UV100 shows the results obtained using the dust temperature expression given by Hocuk (2017) with χUV = 100. The horizontal black lines show the observed abundances relative to CH3OH. The gray boxes represent the 1σ uncertainties. |
Mean confidence level for high-UV field models.
Appendix E Other complementary tables
Observational setups and noise level.
Parameters of the best-fit LTE model.
H2 column densities used to derive chemical abundances.
Indexes of power-law function.
Appendix F Other complementary figures
 |
Fig. F.1 Dust mass opacity spectra for a standard gas-to-dust mass ratio of 100. The dashed lines show the results of Ossenkopf & Henning (1994)’s simulations after 105 yr of dust coagulation with gas densities of 106 cm−3 and 108 cm−3 and for dust grains without ice mantle and with thin ice mantle. The blue solid line shows the κν (of gas) usedto compute H2 column densities in Bonfand et al. (2017). The black solid line shows the κν (of gas)used in this paper, computed with Eq. (4), and based on Ossenkopf & Henning (1994)’s model for grains without ice mantle and for gas densities of 106 cm−3 (magenta dashed line). |
 |
Fig. F.2 Dust mass density profiles derived for Sgr B2(N2-N5) assuming ρd ∝ r−1.5 (Shu 1977). For each source the observational constraint, ρ(r0) = ρ0 is plotted with errorbars (1σ). |
 |
Fig. F.3 Evolution of the total luminosity (L* + Lacc) for a young high-mass protostar assuming a constant accretion rate of Ṁ = 10−4 M⊙ yr−1 (Hosokawa, priv. comm., based on Hosokawa & Omukai 2009). |
 |
Fig. F.4 Panel a: total hydrogen density as a function of time during the quasi-static contraction phase for Sgr B2(N2-N5) for a parcel of gas at a fixed radius, r = rstart (see Sect. 3.5.2 and Table E.4). Panel b: same as (a) but for the visual extinction. |
 |
Fig. F.5 Trajectory of a parcel of gas as function of time in the envelopes of Sgr B2(N2-N5). For each source the parcel of gas is held at a constant radius, rstart (see Table 2), during the whole quasi-static contraction phase. During the free-fall collapse phase, the parcel of gas gradually falls toward the central protostar with the free-fall speed vff (Eq. (12)). |
 |
Fig. F.6 Dust temperature evolution along the trajectory of a parcel of gas infalling toward the central protostar during the free-fall collapse phase for Sgr B2(N2-N5) (red line). In each panel the dashed lines show the dust temperature profiles computed using RADMC-3D with different luminosities (that is at different evolutionary stages). They show how the dust temperature at a given radius in the envelope of each source increases as the total luminosity of the central protostar rises with time (as indicated in the upper right corner). The observational constraint, Td (r0) = T0, used to derive the current luminosity of the source is plotted with errorbars (1σ). |
 |
Fig. F.7 Panel a: gas densities along the trajectory of a parcel of gas gradually infalling through the envelopes of Sgr B2(N2-N5). The quasi-static contraction phase is characterized by the density increasing over time at a constant radius (Fig. F.4a). The subsequent free-fall collapse phase assumes a density distribution propotional to r−1.5. Panel b: visual extinction calculated as a function of the density along the trajectory of a parcel of gas gradually infalling through the envelope. The quasi-static contraction phase is characterized by the extinction increasing over time at a constant radius (Fig. F.4b). During the free-fall collapse phase the extinction increases with the density (Eq. (16)) until Av-max = 500 mag. Panel c: temperature evolution along the trajectory of a parcel of gas gradually infalling through the envelope (see also Fig. F.6). The evolution of the temperature during the quasi-static contraction phase is shown for a minimum temperature Tmin = 15 K (see Fig. 4). |
 |
Fig. F.8 Panel a: gas densities as a function of time along the trajectory of a parcel of gas gradually infalling through the envelope of Sgr B2(N2-N5) (see also Fig. F.5). Panel b: same as (a) for the visual extinction. Panel c: same as (a) for the dust temperature for Tmin = 15 K, up to Tmax = 400 K. |
 |
Fig. F.9 Abundances of 11 COMs with respect to H2 for models N2-CR50 (a), N3-CR50 (b), N4-CR50 (c), and N5-CR50 (d). In each panel the different symbols indicate the abundances calculated at T = 150 K for different minimum dust temperatures. In each panel the horizontal black lines show the observed abundances relative to H2 (Table E.3). The gray boxes show the 1σ uncertainties. The arrow indicates an upper limit. In panel a the chemical abundances lower than 4 × 10−14 are not visible. |
References
- Albertsson, T., Kauffmann, J., & Menten, K. M. 2018, ApJ, 868, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, V., van der Tak, F. F. S., Sánchez-Monge, Á., Cesaroni, R., & Beltrán, M. T. 2017, A&A, 603, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, V., van der Tak, F. F. S., & Walsh, C. 2018, A&A, 616, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2016, Sci. Adv., 2, e1600285 [NASA ADS] [CrossRef] [Google Scholar]
- Ao, Y., Henkel, C., Menten, K. M., et al. 2013, A&A, 550, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, A. T., Longmore, S. N., Avison, A., et al. 2019, MNRAS, 486, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Meshcheryakov, A. A., Garrod, R. T., et al. 2017, A&A, 601, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2019, A&A, 628, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2005, ApJ, 632, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bøgelund, E. G., McGuire, B. A., Ligterink, N. F. W., et al. 2018, A&A, 615, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfand, M., Belloche, A., Menten, K. M., Garrod, R. T., & Müller, H. S. P. 2017, A&A, 604, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botta, O., & Bada, J. L. 2002, Surv. Geophys., 23, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, J. L. 1996, MNRAS, 283, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Chibueze, J. O., Omodaka, T., Handa, T., et al. 2014, ApJ, 784, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Ragan, S. E., Shetty, R., & Klessen, R. S. 2013, ApJ, 768, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2018, A&A, 617, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Belloche, A., Bontemps, S., et al. 2019, A&A, submitted [Google Scholar]
- De Pree, C. G., Goss, W. M., & Gaume, R. A. 1998, ApJ, 500, 847 [NASA ADS] [CrossRef] [Google Scholar]
- De Pree, C. G., Peters, T., Mac Low, M. M., et al. 2015, ApJ, 815, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Enrique-Romero, J., Rimola, A., Ceccarelli, C., & Balucani, N. 2016, MNRAS, 459, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Fleck, A. J., & Canfield, E. H. 1983, J. Chem. Phys., 54, 508 [Google Scholar]
- Garrod, R. T. 2008, A&A, 491, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Pauly, T. 2011, ApJ, 735, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Belloche, A., Müller, H. S. P., & Menten, K. M. 2017, A&A, 601, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaume, R. A., Claussen, M. J., de Pree, C. G., Goss, W. M., & Mehringer, D. M. 1995, ApJ, 449, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Brand, J., Sánchez-Monge, Á., et al. 2013, A&A, 556, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Ginsburg, A., Henkel, C., Ao, Y., et al. 2016, A&A, 586, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Bally, J., Barnes, A., et al. 2018, ApJ, 853, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., & Langer, W. D. 1974, ApJ, 193, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1978, ApJ, 222, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, A. E., Sanhueza, P., Contreras, Y., et al. 2015, ApJ, 815, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Hayakawa, S., Nishimura, S., & Takayanagi, T. 1961, PASJ, 13, 184 [NASA ADS] [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hocuk, S., Szűcs, L., Caselli, P., et al. 2017, A&A, 604, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollis, J. M., Lovas, F. J., & Jewell, P. R. 2000, ApJ, 540, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Lovas, F. J., Remijan, A. J., et al. 2006, ApJ, 643, L25 [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. L., & Moore, M. H. 2001, J. Geophys. Res., 106, 33275 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Iqbal, W., Wakelam, V., & Gratier, P. 2018, A&A, 620, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffreson, S. M. R., Kruijssen, J. M. D., Krumholz, M. R., & Longmore, S. N. 2018, MNRAS, 478, 3380 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, I. N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017, A&A, 603, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. M. D., Longmore, S. N., Elmegreen, B. G., et al. 2014, MNRAS, 440, 3370 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Ruaud, M., Bron, E., et al. 2016, A&A, 585, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., & Goldsmith, P. F. 1990, ApJ, 356, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Serabyn, E., Zylka, R., & Li, Y. 2001, ApJ, 550, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Longmore, S. N., Rathborne, J., Bastian, N., et al. 2012, ApJ, 746, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., Bardeau, S., & Reynier, E. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A. 2018, ApJS, 239, 17 [Google Scholar]
- Mehringer, D. M., Palmer, P., Goss, W. M., & Yusef-Zadeh, F. 1993, ApJ, 412, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Mehringer, D. M., Snyder, L. E., Miao, Y., & Lovas, F. J. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M. 2004, in The Dense Interstellar Medium in Galaxies, eds. S. Pfalzner, C. Kramer, C. Staubmeier, & A. Heithausen (Berlin: Springer), 91, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Xu, L.-H., et al. 2016, A&A, 587, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2017, ApJ, 845, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Geballe, T. R., Goto, M., Usuda, T., & McCall, B. J. 2005, ApJ, 632, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V.,& Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ott, J., Weiß, A., Staveley-Smith, L., Henkel, C., & Meier, D. S. 2014, ApJ, 785, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1958, Phys. Rev., 110, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Pauly, T., & Garrod, R. T. 2016, ApJ, 817, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Müller, H. S. P., Pickett, H. M., Cohen, E. A., & Drouin, B. J. 2010, J. Quant. Spectr. Rad. Transf., 111, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Mac Low, M.-M., Banerjee, R., Klessen, R. S., & Dullemond, C. P. 2010, ApJ, 719, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., & Mac Low, M.-M. 2011, ApJ, 729, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S.-L., Schilke, P., Rolffs, R., et al. 2011, A&A, 530, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quénard, D., Jiménez-Serra, I., Viti, S., Holdship, J., & Coutens, A. 2018, MNRAS, 474, 2796 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Longmore, S. N., Jackson, J. M., et al. 2014, ApJ, 786, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Remijan, A. J. 2015, IAU General Assembly, 22, 2257092 [NASA ADS] [Google Scholar]
- Rimmer, P. B., Herbst, E., Morata, O., & Roueff, E. 2012, A&A, 537, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothard, H., Domaracka, A., Boduch, P., et al. 2017, J. Phys. B At. Mol. Phys., 50, 062001 [Google Scholar]
- Sánchez-Monge, Á., Schilke, P., Schmiedeke, A., et al. 2017, A&A, 604, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmiedeke, A., Schilke, P., Möller, T., et al. 2016, A&A, 588, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shingledecker, C. N., Tennis, J., Le Gal, R., & Herbst, E. 2018, ApJ, 861, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Skouteris, D., Balucani, N., Ceccarelli, C., et al. 2018, ApJ, 854, 135 [Google Scholar]
- Spitzer, J. L., & Tomasko, M. G. 1968, ApJ, 152, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Terrier, R., Clavel, M., Soldi, S., et al. 2018, A&A, 612, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umebayashi, T., & Nakano, T. 1981, PASJ, 33, 617 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., Belloche, A., Schilke, P., et al. 2006, A&A, 454, L99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viti, S., Girart, J. M., Garrod, R., Williams, D. A., & Estalella, R. 2003, A&A, 399, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Selsis, F., Herbst, E., & Caselli, P. 2005, A&A, 444, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., & Selsis, F. 2006, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, D. L., Longmore, S. N., Zhang, Q., et al. 2018, MNRAS, 474, 2373 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Tielens, A. G. G. M., et al. 1998, ApJ, 498, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Wilcock, L. A., Ward-Thompson, D., Kirk, J. M., et al. 2012, MNRAS, 422, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, E. R., & Garrod, R. T. 2017, ApJ, 840, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, M., Sandell, G., Wilner, D. J., & Plambeck, R. L. 1992, ApJ, 393, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrowski, F., Schilke, P., Walmsley, C. M., & Menten, K. M. 1999, ApJ, 514, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Muno, M., Wardle, M., & Lis, D. C. 2007, ApJ, 656, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Zucconi, A., Walmsley, C. M., & Galli, D. 2001, A&A, 376, 650 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Dust temperature profiles computed for Sgr B2(N2-N5) using RADMC-3D, assuming a dust mass density distribution proportional to r−1.5 (Fig. F.2). The observational constraint Td(r0) = T0 used to estimate the current luminosity of each source is plotted with errorbars (1σ). |
| In the text | |
 |
Fig. 2 Panela: accretion rate evolution for a young high-mass protostar approximated from the RMHD simulations of Peters et al. (2011; dashed lines). Panel b: time evolution of the protostar’s mass derived from its accretion rate, Ṁ (t) (panel a, dashed line). Panel c: time evolution of the protostar’s total luminosity derived from its mass, M (t) (panel b, dashed line), using the Hosokawa & Omukai (2009) mass-luminosity relation (Fig. F.3). Inall panels the solid line shows the result obtained when keeping a constant accretion rate (10−4 M⊙ yr−1) after ~6 × 104 yr. |
| In the text | |
 |
Fig. 3 Two-stage physical model assumed for the time evolution of Sgr B2(N2-N5). The physical properties derived at the boundaries of each stage are shown in boxes (see also Table 2). The parameters that are common to all sources are highlighted in boldface. The evolution of the physical parameters during each stage is indicated in green with arrows. The evolution of Td during the first stage depends on the adopted minimum dust temperature (see Sect. 3.5.1). |
| In the text | |
 |
Fig. 4 Dust temperature as a function of time during the quasi-static contraction phase (Eq. (11)). Temperatures are computed for a constant radius, r = rstart, and for threedifferent Tmin. |
| In the text | |
 |
Fig. 5 Panel a: column densities of 11 COMs detected toward Sgr B2(N2-N5) (see Table E.2). The error bars show uncertainties on the derived column densities (1σ, see Sect. A). Panel b: chemical abundances relative to H2 of the COMs shown in panel a. The error bars show uncertainties that also include the uncertainty on the H2 column density (1σ, see Sect. 3.1). Panel c: abundances relative to CH3OH of the COMsshown in panel a. The error bars represent 1σ uncertainties on the derived ratios. |
| In the text | |
 |
Fig. 6 Evolution of the ice-mantle and gas-phase chemistry during the cold quasi-static contraction phase. The results from the standard models N(2-5)-T15-CR1 are displayed from top to bottom. Panel a: calculated fractional ice-mantle composition by ice layer. Panel b: cumulative fractional composition of the ices with respect to water, summed over the grain mantle up to an ice thickness given on the abscissa. Panel c: gas-phase fractional abundances (with respect to total hydrogen) of atomic and simple diatomic species as a function of time with the same time axis as panels a and b to facilitate the comparison. |
| In the text | |
 |
Fig. 7 Calculated fractional abundances for 11 COMs detected toward Sgr B2(N2-N5). Panels a: N-bearing species C2H5CN, C2H3CN, CH3CN, NH2CHO, and CH3NCO, as well as CH3SH. Panels b: O-bearing species CH3OH, C2H5OH, CH3OCHO, CH3OCH3, and CH3CHO. The results for the standard models, N(2-5)-T15-CR1, are shown from top to bottom, as a function of the temperature in the envelope of the sources during the free-fall collapse phase. In each panel the timescale shown at the top is derived from the time-dependent evolution of the temperature in the envelopes of the sources (see Sect. 3.5.2). In each panel, the solid lines show the fractional abundances (with respect to total hydrogen) in the gas phase while the dotted lines show the abundances of the same species on the grains (ice surface+mantle). |
| In the text | |
 |
Fig. 8 Fractional abundances (with respect to total hydrogen) calculated for the standard models at the end of the simulations (that is at T = 400 K). |
| In the text | |
 |
Fig. 9 Panel a: composition of the ice-mantles built up during the cold quasi-static contraction phase prior to the free-fall collapse for the model N2-T10-CR1. Panel b: same as a but for the model N2-T20-CR1. |
| In the text | |
 |
Fig. 10 Calculated fractional abundances (with respect to total hydrogen) of 11 COMs at the end of the simulations (that is T = 400 K) for the models N2-CR1 (panel a), N3-CR1 (panel b), N4-CR1 (panel c), and N5-CR1 (panel d), assuming a standard CRIR and different Tmin: 10 K in blue, 15 K in purple, and 20 K in red (see Table 3). |
| In the text | |
 |
Fig. 11 Composition of the ice mantles built up during the cold quasi-static contraction phase for models N2-T15-CR10 (panel a), N2-T15-CR100 (panel b), and N2-T15-CR1000 (panel c). |
| In the text | |
 |
Fig. 12 Calculated gas-phase fractional abundances (with respect to total hydrogen) of 11 COMs obtained at the end of the simulations for model N2-T15 (panel a), N3-T15 (panel b), N4-T15 (panel c), and N5-T15 (panel d), with different CRIR values as shown in Table 3. Species with fractional abundances lower than 10−15 are not visible in the histograms. |
| In the text | |
 |
Fig. 13 From top to bottom: abundances of ten COMs with respect to CH3OH calculated atT = 150 K by the models N2-N5, with different Tmin. In each panel the different symbols indicate the abundances calculated with different CRIR values. The horizontal black lines show the observed abundances relative to CH3OH. The gray boxes represent the 1σ uncertainties. Arrows indicate upper limits. The abundances relative to CH3OH lower than 10−9 are not visible in the plots. |
| In the text | |
 |
Fig. 14 Panel a: matrice of confidence levels of the models with respect to the observed abundances of ten COMs relative to H2. The first four panels in this column show, from top to bottom, the results for Sgr B2(N2), N3, N4, and N5, respectively. Bottom panel: average matrice for all four hot cores taken together. Panel b: same as (a) but only for the O-bearing species CH3OH, CH3OCHO, CH3OCH3, CH3CHO, C2H5OH, and NH2CHO. Panel c: same as (a) but only for the cyanides CH3CN, C2H5CN, and C2H3CN. |
| In the text | |
 |
Fig. 15 Panel a: matrice of confidence levels of the models with respect to the observed abundances of nine COMs relative to CH3OH. The first four panels in this column show, from top to bottom, the results for Sgr B2(N2), N3, N4, and N5, respectively. The bottom panel shows the average matrice for all four hot cores taken together. Panel b: same as (a) but for the abundances relative to CH3OH of the O-bearing species CH3OCHO, CH3OCH3, CH3CHO, C2H5OH, and NH2CHO only. Panel c: same as (a) but for the abundances relative to CH3CN of the cyanides C2H5CN and C2H3CN only. |
| In the text | |
 |
Fig. 16 Calculated fractional abundances of C2H5CN with respect to C2H3CN as a function of the CRIR. In each panel, the different symbols indicate the abundances calculated at T = 150 K for different minimum dust temperatures and the horizontal black line shows the observed ratio. Uncertainties (1σ) are shown in gray. The [C2H5CN]/[C2H3CN] ratios obtained for models N3-CR500 ad N3-CR1000 (<10−2) are not displayed. |
| In the text | |
 |
Fig. B.1 Growth of the dust-grain ice mantles over time during the quasi-static contraction phase for the standard models N(2-5)-T15-CR1. |
| In the text | |
 |
Fig. B.2 Calculated fractional abundances of 11 COMs for models N2-T10-CR1 (top panels) and N2-T20-CR1 (bottom panels), plotted as a function of temperature in the envelope of Sgr B2(N2) during the free-fall collapse phase. In each panel the timescale shown at the top is derived from the time-dependent evolution of the temperature along the trajectory of the infalling parcel of gas (see Sect. 3.5.2). In each panel, the solid lines show the fractional abundances (with respect to total hydrogen) in the gas phase while the dotted lines show the abundances of the same species on the grains (ice-surface+mantle). |
| In the text | |
 |
Fig. B.3 Same as B.2 but for models N3-T10-CR1 (top panels) and N3-T20-CR1 (bottom panels). |
| In the text | |
 |
Fig. B.4 Same as B.2 but for models N4-T10-CR1 (top panels) and N4-T20-CR1 (bottom panels). |
| In the text | |
 |
Fig. B.5 Same as B.2 but for models N5-T10-CR1 (top panels) and N5-T20-CR1 (bottom panels). |
| In the text | |
 |
Fig. B.6 Same as B.2 but for models N2-T15-CR10 (top panels), N2-T15-CR100 (middle panels), and N2-T15-CR1000 (bottom panels). |
| In the text | |
 |
Fig. B.7 Same as B.2 but for models N3-T15-CR10 (top panels), N3-T15-CR100 (middle panels), and N3-T15-CR1000 (bottom panels). |
| In the text | |
 |
Fig. B.8 Same as B.2 but for models N4-T15-CR10 (top panels), N4-T15-CR100 (middle panels), and N4-T15-CR1000 (bottom panels). |
| In the text | |
 |
Fig. B.9 Same as B.2 but for models N5-T15-CR10 (top panels), N5-T15-CR100 (middle panels), and N5-T15-CR1000 (bottom panels). |
| In the text | |
 |
Fig. D.1 Chemical abundances with respect to CH3OH of ten COMscalculated at T = 150 K by the models N2-CR50. The different symbols indicate the abundances calculated with different χUV. Model Tdhoc-UV100 shows the results obtained using the dust temperature expression given by Hocuk (2017) with χUV = 100. The horizontal black lines show the observed abundances relative to CH3OH. The gray boxes represent the 1σ uncertainties. |
| In the text | |
 |
Fig. F.1 Dust mass opacity spectra for a standard gas-to-dust mass ratio of 100. The dashed lines show the results of Ossenkopf & Henning (1994)’s simulations after 105 yr of dust coagulation with gas densities of 106 cm−3 and 108 cm−3 and for dust grains without ice mantle and with thin ice mantle. The blue solid line shows the κν (of gas) usedto compute H2 column densities in Bonfand et al. (2017). The black solid line shows the κν (of gas)used in this paper, computed with Eq. (4), and based on Ossenkopf & Henning (1994)’s model for grains without ice mantle and for gas densities of 106 cm−3 (magenta dashed line). |
| In the text | |
 |
Fig. F.2 Dust mass density profiles derived for Sgr B2(N2-N5) assuming ρd ∝ r−1.5 (Shu 1977). For each source the observational constraint, ρ(r0) = ρ0 is plotted with errorbars (1σ). |
| In the text | |
 |
Fig. F.3 Evolution of the total luminosity (L* + Lacc) for a young high-mass protostar assuming a constant accretion rate of Ṁ = 10−4 M⊙ yr−1 (Hosokawa, priv. comm., based on Hosokawa & Omukai 2009). |
| In the text | |
 |
Fig. F.4 Panel a: total hydrogen density as a function of time during the quasi-static contraction phase for Sgr B2(N2-N5) for a parcel of gas at a fixed radius, r = rstart (see Sect. 3.5.2 and Table E.4). Panel b: same as (a) but for the visual extinction. |
| In the text | |
 |
Fig. F.5 Trajectory of a parcel of gas as function of time in the envelopes of Sgr B2(N2-N5). For each source the parcel of gas is held at a constant radius, rstart (see Table 2), during the whole quasi-static contraction phase. During the free-fall collapse phase, the parcel of gas gradually falls toward the central protostar with the free-fall speed vff (Eq. (12)). |
| In the text | |
 |
Fig. F.6 Dust temperature evolution along the trajectory of a parcel of gas infalling toward the central protostar during the free-fall collapse phase for Sgr B2(N2-N5) (red line). In each panel the dashed lines show the dust temperature profiles computed using RADMC-3D with different luminosities (that is at different evolutionary stages). They show how the dust temperature at a given radius in the envelope of each source increases as the total luminosity of the central protostar rises with time (as indicated in the upper right corner). The observational constraint, Td (r0) = T0, used to derive the current luminosity of the source is plotted with errorbars (1σ). |
| In the text | |
 |
Fig. F.7 Panel a: gas densities along the trajectory of a parcel of gas gradually infalling through the envelopes of Sgr B2(N2-N5). The quasi-static contraction phase is characterized by the density increasing over time at a constant radius (Fig. F.4a). The subsequent free-fall collapse phase assumes a density distribution propotional to r−1.5. Panel b: visual extinction calculated as a function of the density along the trajectory of a parcel of gas gradually infalling through the envelope. The quasi-static contraction phase is characterized by the extinction increasing over time at a constant radius (Fig. F.4b). During the free-fall collapse phase the extinction increases with the density (Eq. (16)) until Av-max = 500 mag. Panel c: temperature evolution along the trajectory of a parcel of gas gradually infalling through the envelope (see also Fig. F.6). The evolution of the temperature during the quasi-static contraction phase is shown for a minimum temperature Tmin = 15 K (see Fig. 4). |
| In the text | |
 |
Fig. F.8 Panel a: gas densities as a function of time along the trajectory of a parcel of gas gradually infalling through the envelope of Sgr B2(N2-N5) (see also Fig. F.5). Panel b: same as (a) for the visual extinction. Panel c: same as (a) for the dust temperature for Tmin = 15 K, up to Tmax = 400 K. |
| In the text | |
 |
Fig. F.9 Abundances of 11 COMs with respect to H2 for models N2-CR50 (a), N3-CR50 (b), N4-CR50 (c), and N5-CR50 (d). In each panel the different symbols indicate the abundances calculated at T = 150 K for different minimum dust temperatures. In each panel the horizontal black lines show the observed abundances relative to H2 (Table E.3). The gray boxes show the 1σ uncertainties. The arrow indicates an upper limit. In panel a the chemical abundances lower than 4 × 10−14 are not visible. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


