| Issue |
A&A
Volume 659, March 2022
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202142004 | |
| Published online | 11 March 2022 | |
Retrieving cosmological information from small-scale CMB foregrounds
I. The thermal Sunyaev Zel’dovich effect
1
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, 91405 Orsay, France
e-mail: [email protected]
2
INAF – Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
3
Department of Physics and McGill Space Institute, McGill University, Montreal, QC H3A 2T8, Canada
Received:
11
August 2021
Accepted:
7
December 2021
We propose a new analysis of small-scale cosmic microwave background (CMB) data by introducing the cosmological dependency of the foreground signals, focussing first on the thermal Sunyaev-Zel’dovich (tSZ) power spectrum, derived from the halo model. We analyse the latest observations by the South Pole Telescope (SPT) of the high-ℓ power (cross) spectra at 95, 150, and 220 GHz, as the sum of CMB and tSZ signals, both depending on cosmological parameters and remaining contaminants. In order to perform faster analyses, we propose a new tSZ modelling based on machine learning algorithms (namely Random Forest). We show that the additional information contained in the tSZ power spectrum tightens constraints on cosmological and tSZ scaling relation parameters. We combined for the first time the Planck tSZ data with SPT high-ℓ to derive new constraints. Finally, we show how the amplitude of the remaining kinetic SZ power spectrum varies depending on the assumptions made on both tSZ and cosmological parameters. These results show the importance of a thorough modelling of foregrounds in the cosmological analysis of small-scale CMB data. Reliable constraints on cosmological parameters can only be achieved once other significant foregrounds, such as the kinetic SZ and the cosmic infrared background (CIB), are also properly accounted for.
Key words: methods: numerical / cosmic background radiation / cosmological parameters / large-scale structure of Universe
© M. Douspis et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Observations in millimetre wavelengths for cosmic microwave background (CMB) analysis contain, at small (arcmin) scales, a sum of signals originating from sources ranging from the last scattering surface to our local environment. At these scales, the primordial CMB signal fades away compared to secondary anisotropies and contaminants created along the path of photons. Among these, the thermal and kinetic Sunyaev-Zel’dovich effects (tSZ and kSZ, respectively; Zeldovich & Sunyaev 1969; Sunyaev & Zeldovich 1980), which stem from the interaction between CMB photons and the large-scale structure of the recent Universe, contain information of cosmological interest.
The inverse Compton effect of CMB photons on energetic electrons from hot gas in galaxy clusters and groups (and thus filaments) is responsible for the tSZ anisotropies and additional power at small scales in the angular power spectrum of CMB fluctuations. Such an effect is frequency-dependent, a property which allows one to separate tSZ signal from other components in CMB data and reconstruct both a tSZ map (Planck Collaboration XXI 2014; Planck Collaboration XXII 2016; Aghanim et al. 2019; Madhavacheril et al. 2020; Bleem et al. 2022; Tanimura et al. 2022) and power spectrum (Planck Collaboration XXI 2014; Planck Collaboration XXII 2016; Tanimura et al. 2022). The power spectrum amplitude and shape of this secondary anisotropy are highly dependent on the number of halos and their distribution in mass and redshift, and thus on the cosmological model considered. Typically, the amplitude of the tSZ spectrum varies with the normalisation of the matter power spectrum as  and the total matter content of our Universe as
and the total matter content of our Universe as  (see, e.g. Hurier & Lacasa 2017; Salvati et al. 2018; Bolliet et al. 2018). As the cluster mass is never observed directly, the tSZ amplitude also depends on the modelling and calibration of the scaling relation (SR) between the mass and the observable, that is the gas pressure.
(see, e.g. Hurier & Lacasa 2017; Salvati et al. 2018; Bolliet et al. 2018). As the cluster mass is never observed directly, the tSZ amplitude also depends on the modelling and calibration of the scaling relation (SR) between the mass and the observable, that is the gas pressure.
On the other hand, the kSZ effect is produced by induced Doppler shift of the scattered CMB photons off free electrons with a bulk velocity with respect to the CMB rest-frame. It has the same frequency dependency as CMB photons. Due to this interaction, anisotropies are created at two epochs: first, during the reionisation era, as the effect depends on the number and distribution of free electrons, and at later times in large-scale structures – typically, clusters (Aghanim et al. 1996; Schaan et al. 2021). These anisotropies translate into an additional power spectrum, peaking at small scales, for which the shape and amplitude depends on the reionisation history (Zahn et al. 2005; Planck Collaboration XLVII 2016; Gorce et al. 2020). At the same millimetre wavelengths, galaxies may contribute to the observed signal by emission in the radio (synchrotron of active galactic nuclei) or infrared (dusty galaxies) domains, and even dominate at smaller scales.
Most current analyses of CMB observations at small scales are done following the same approach (see, e.g., George et al. 2015; Couchot et al. 2017; Reichardt et al. 2021; Han et al. 2021). A theoretical CMB power spectrum is added to templates of each non-CMB signal to reproduce the observed power spectrum. As mentioned above, apart from the tSZ and kSZ effects, the remaining non-CMB components are thermal dust emission from dusty star-forming galaxies (DSFG) – both the Poisson and spatially clustered component, the radio galaxy emission, the Galactic cirrus signal and the cosmic infrared background (CIB). The cosmological parameters enter only the CMB power spectrum, whilst the amplitudes of all templates are set free and marginalised over:
where Θ is the set of free cosmological parameters and D3000, i is the free amplitude of a template Ti for foreground component i, normalised to one at ℓ = 3000. All but CMB signals are considered nuisance quantities and the cosmological information is retrieved only from the CMB part1. Little to no astrophysical information can be derived from the secondary anisotropies, unless it is directly contained in the amplitude of their spectra. Such analyses may also include inconsistencies in the assumptions made in the different templates and in the CMB computation: a typical example is the cosmological parameters assumed in the simulation used to derive the tSZ template that may be different from the one used for the kSZ template, and from the resulting, best-fit cosmological parameters – see, for example, discussions in George et al. (2015) and Reichardt et al. (2021).
Our goal, here, is to use the full cosmological information contained in both primordial and secondary anisotropy power spectra, in order to get tighter constraints on the main cosmological parameters and at the same time on the physical parameters related to secondary anisotropies. Our approach is to substitute templates of the non-CMB signal with models for the power spectra that encompass the full cosmological information.
As a first step, we focus on the tSZ effect, proposing also a new way to compute efficiently its angular power spectrum at high ℓ, including it in the traditional Monte Carlo Markov chains approach. Doing so, we are able to put constraints on cosmological parameters, cluster models and residual kSZ amplitude:
where Σ is the set of scaling relation parameters and j runs over all the remaining non-CMB components.
We apply our approach to the South Pole Telescope (SPT) data presented in Reichardt et al. (2021), which spans a range of scales and frequencies where the SZ signal dominates the primordial CMB, and to the Planck-tSZ data of Tanimura et al. (2022). We investigate the impact of this new approach on cosmological, scaling relation parameters and kSZ amplitude constraints. A companion paper will present how, in addition, the kSZ template could be substituted by a more physical modelling, presented in Gorce et al. (2020), to derive information on the Epoch of Reionisation (Gorce et al. 2022).
The next section details the ingredients required to compute the tSZ power spectrum from the halo model and introduces the scaling relation (SR) parameters. A sub-section presents a new technique introduced in this paper to speed up the computation of the tSZ power spectrum, based on machine learning. Section 3 introduces the SPT and Planck-tSZ data used in our analysis and the details of the MCMC settings. Section 4 shows the changes in constraints obtained with our approach on cosmological and SR parameters. Finally, we discuss how the significance of the resulting kSZ power amplitude may change depending on the assumptions on the tSZ contribution. The assumed cosmological and scaling parameters and their respective priors are summarised in Appendix A.
2. The tSZ angular power spectrum
In this section, we present the adopted theoretical model for the tSZ power spectrum and describe the machine learning method used to evaluate the tSZ signal in the MCMC sampling.
2.1. Theoretical evaluation
For the theoretical evaluation of the tSZ power spectrum, we follow the approach discussed in Planck Collaboration XXII (2016) and Salvati et al. (2018). For the complete discussion, we refer the reader to these works and report here only the main steps of the derivation.
We adopt the halo model (see, e.g., Cooray 2000), and write the total tSZ power spectrum as the sum of a one-halo and a two-halo term
Under the flat-sky approximation, the one-halo term is defined as
In the above equation, dn(M500, z)/dM500 is the halo mass function, and dV/(dz dΩ) is the comoving volume element (per unit of redshift and solid angle). We assume M500/[M⊙ h−1] ∈ [1013, 5 × 1016], z ∈ [0, 3]. For the halo mass function, we adopt the formulation described in Tinker et al. (2008). The term  represents the Fourier transform, on a sphere, of the Compton parameter y. Following the Limber approximation, it is defined as
represents the Fourier transform, on a sphere, of the Compton parameter y. Following the Limber approximation, it is defined as
For the pressure profile Pe(M500, z, x), we adopt the universal formulation provided in Arnaud et al. (2010), with rs being the scale radius and x = r/rvs. The multipole ℓs is defined from the angular diameter distance DA(z), such that ℓs = DA(z)/rs.
The two-halo term can be defined as
In the above equation, P(k, z) is the matter power spectrum and B(M500, z) is the time-dependent linear bias factor which relates the correlation function of the tSZ signal to the underlying matter power spectrum. Following Komatsu & Kitayama (1999), we define the bias as
where ν(M500, z) = δc(M500)/D(z) σ(M500). Here, D(z) is the linear growth factor, and δc(z) is the over-density threshold for the spherical collapse. The term σ(M500) is the standard deviation of density perturbations, at present time, in a sphere of radius R = (3M500/4πρm, 0), defined as
where W(kR) is the window function of a spherical top-hat of radius R. In the remaining of this work, we may refer to the  as Cℓ when there is no ambiguity, but always put attributes when we refer to other components (CMB, kSZ, CIB, …).
as Cℓ when there is no ambiguity, but always put attributes when we refer to other components (CMB, kSZ, CIB, …).
We also take into account the non-Gaussian contribution to the cosmic variance, defined by the trispectrum Tℓℓ′. Following Komatsu & Seljak (2002) and Horowitz & Seljak (2017), the dominant term of the trispectrum in the halo model is
2.2. Scaling relations
As mentioned above, the halo mass cannot be measured directly. We need, therefore, to define a scaling relation between the chosen observable and the mass. For the tSZ effect, we can define this relation starting from the integrated Compton-y parameter, Y500. Following Planck Collaboration XXII (2016), it reads:
with a dispersion σlnY = 0.17. In the above equation, DA(z) is the angular diameter distance, and E(z)≡H(z)/H0. The parameters β, Y*, α, (1 − b) are obtained by calibrating this scaling relation with external multi-wavelength data. In particular, we can assume that clusters follow a self-similar evolution, which implies β = 2/3. The Y* and α parameters are constrained from X-ray data. The parameter b represents the mass bias and it is related to the ratio between the tSZ mass, evaluated from the pressure profile assuming hydrostatic equilibrium, and the real cluster mass M500, such that (1 − b)≡MSZ/M500. This mass bias is calibrated with weak lensing observations. We refer the interested reader to Planck Collaboration XXII (2016) for additional details of the definition and general calibration process of the scaling relation.
2.3. Machine learning approach
The derivation of the tSZ power spectrum as described in Sect. 2.1 implies the computation and integration of the Fourier transform of the Compton-y parameter over a large range of masses, redshifts and k-modes. As the multipole range increases towards higher ℓ with high resolution instruments like SPT, the time to compute the  ’s increases and slows down the sampling. Therefore, we turn to machine learning techniques to approximate the full Cℓ’s computed above (hereafter ‘true Cℓ’s’) to speed up the MCMC runs (see also Spurio Mancini et al. 2021 for the development of an emulator for CMB and large-scale structure analyses).
’s increases and slows down the sampling. Therefore, we turn to machine learning techniques to approximate the full Cℓ’s computed above (hereafter ‘true Cℓ’s’) to speed up the MCMC runs (see also Spurio Mancini et al. 2021 for the development of an emulator for CMB and large-scale structure analyses).
Among the numerous existing machine learning techniques, we choose a Random Forest (RF) algorithm. Random Forest is a supervised machine-learning algorithm which bootstraps the training set in order to construct independent decision trees. The final prediction is the mean of the outputs of the different trees. The training set is divided into a learning set, a validation set and a testing set, constructed to evaluate potential bias and errors in the prediction. Random Forest has generated great interest in recent astrophysical and cosmological analyses (e.g. Bonjean et al. 2019; Hernandez Vivanco et al. 2020; Kennedy et al. 2021), because it achieves high accuracy and efficiency with large data sets, whilst being quick to implement. Additionally, at the training stage, RF is able to learn in a fast way highly non-linear relations between the inputs and the outputs it is given. For these reasons, we implement this particular machine-learning technique in our analysis.
We build a training set with a random sampling of an eight-dimensional space of cosmological and scaling relation parameters as inputs: five cosmological parameters (Ωb, Ωm, σ8, ns and h) and three scaling relation parameters (1 − b, Y⋆, α), on a wide range including their fiducial values (see last column of Table A.1 for precise ranges). The outputs consist of the corresponding Cℓ’s computed at 10 different ℓ-bins between 10 and 10 000. Given the smoothness of the power spectrum, we find this number of bins to be sufficient to recover by interpolation the ℓ-by-ℓ power spectrum required by the likelihood for the cosmological analysis.
We use a sample of 15 000 models divided into fifths such that 60%, 20% and 20% of the models are used for the learning, validation, and testing phase, respectively. In order to facilitate the learning, we pre-process the Cℓ’s by rescaling them accordingly to their order zero amplitude variation at ℓ = 3000 with the cosmological and scaling parameters. For example, the learning is done on  instead of Cℓ. Doing so, the RF only needs to learn the shape and variation around
instead of Cℓ. Doing so, the RF only needs to learn the shape and variation around  instead of the full dependency. We generalise this procedure to all considered parameters, such that the RF learning phase is done on
instead of the full dependency. We generalise this procedure to all considered parameters, such that the RF learning phase is done on  with:
with:
The exponent of each parameter is obtained by minimising the spread of the  distribution for all the parameters in the training set. We find that pre-processing the data in this way improves the score of the prediction by 5%.
distribution for all the parameters in the training set. We find that pre-processing the data in this way improves the score of the prediction by 5%.
To further improve the accuracy of the prediction, a possibility is to optimise the choice of RF hyper parameters. In this perspective, we test different numbers of trees and depths and choose, respectively, 40 and 20, as they maximise the final score of the prediction to 96.2%2, whilst limiting memory and time imprints.
An example of the quality of the RF-inferred Cℓ’s versus ‘true’ ones is shown for a sample of ten random models, picked within the testing set, in Fig. 1. This technique reproduces well the true Cℓ’s with an overall gain in computation time of about two orders of magnitude. To further improve the computation time, one could use another emulator to predict the CMB power spectrum instead of using a Boltzman integrator in the analysis (Spurio Mancini et al. 2021). We find that the true Cℓ’s and the RF Cℓ’s overall agree at better than the 2% level. As seen on Fig. 1, this corresponds to 0.08 μK2 at ℓ = 3000, which is below the error of current measurements: ∼1.08 μK2 at ℓ = 3000 at 2σ (Reichardt et al. 2021). However, a better reconstruction might be required for future observations.
 |
Fig. 1. Comparison of the ‘true’ tSZ Cℓ’s values at given ℓ (crosses, and solid lines) with the RF-inferred Cℓ’s after interpolation (dashed lines) for a sample of models (units are arbitrary before renormalisation in y-units at 143 GHz). The lower part of the plot shows the ratio of RF Cℓ’s over ‘true’ Cℓ’s. The grey areas are showing the 68% and 95% dispersion among the test set. |
3. Data and method
In this section, we describe the different datasets used in our analysis and the approach we adopt for the MCMC sampling of the parameter space.
3.1. SPT 2020
We consider the observed signal on small scales (high multipoles ℓ) and, therefore, make use of the SPT temperature-only data and likelihood introduced in Reichardt et al. (2021) and made publicly available by the authors3. We refer the interested reader to this work for details on the dataset, but highlight the fact that the data considered spans the range 2000 ≤ ℓ ≤ 11 000 at frequencies 95, 150 and 220 GHz. The likelihood makes use of auto- and cross-spectra and marginalises over calibration and beam parameters. In the baseline analysis of Reichardt et al. (2021), the total signal is modelled by CMB, tSZ, kSZ, galactic cirrus contamination, radio and infrared galaxies spectra and tSZ-CIB cross-spectra. In this work, we modified only the tSZ spectra and consequently the tSZ-CIB cross spectra contributions, computed in the SPT likelihood as the sampled correlation coefficient times a function of the tSZ Cℓ’s (as defined in Zahn et al. 2012). Implementing new CIB and kSZ modelling will be the focus of upcoming works.
3.2. Planck tSZ
To complement the high-ℓ SPT data, we consider the Planck21-tSZ power spectrum estimated by Tanimura et al. (2022, hereafter T21), an update of the Planck Collaboration analyses (Planck Collaboration XXI 2014; Planck Collaboration XXII 2016) but using the Planck frequency maps from the public data release PR4 (Planck Collaboration LVII 2020). The scales covered by Planck21-tSZ are 60 < ℓ < 1400 and do not overlap with those covered by SPT. Hence, there is no need to consider correlations between the two experiments when combining the data sets. When using Planck21-tSZ data, we consider the map power spectrum and marginalise over residual foregrounds amplitudes (CIB, IR and radio point sources, and residual high-ℓ noise), as done and described in T21, such that
We thus build our Planck21-tSZ likelihood, assuming Gaussian priors on the foreground dimensionless amplitudes centred on one and with a standard deviation of 0.5 (T21). In addition to the statistical error bars, we also consider the error term coming from the trispectrum contribution and defined as (see, e.g., Komatsu & Seljak 2002; Horowitz & Seljak 2017)
where we use fsky = 0.42, to be consistent with T21 analysis. To ease the computation while using the RF Cℓ’s, we approximate the ℓ-by-ℓ trispectrum term σTℓℓ′ with a constant value over the full multipole range. We consider the mean value of Eq. (13), evaluated at the fiducial cosmology. We keep this value independently of the cosmological model considered, as we made sure that this approximation only introduces a negligible uncertainty with respect to the total error budget. Additionally, in Sect. 4, we show that this approximation has no impact on the inference of cosmological and scaling relation parameters.
3.3. MCMC
We make use of the publicly available Monte Carlo Markov chain CosmoMC code (Lewis & Bridle 2002; Lewis 2013), that we modify to include both the SPT high-ℓ and the Planck21-tSZ likelihoods, as well as the RF prediction of the tSZ power spectrum. We sample simultaneously cosmological and scaling relation parameters. For the cosmological model, we consider five standard parameters, that is the baryon and cold dark matter densities, Ωbh2 and Ωch2; the ratio of the sound horizon to the angular diameter distance at decoupling θ; the scalar spectral index, ns; the overall normalisation of the spectrum, As; the reionisation optical depth τ is assumed fixed. For the scaling relations, we follow the discussion in Sect. 2.2 and, therefore, sample three parameters, that is the mass bias (1 − b), the mass slope α and the normalisation Y*. As stated in Sect. 2.2, we assume the self-similar evolution for halos, and fix β = 2/3.
We focus our analysis on the following cosmological parameters: Ωm, σ8, H0, and the mass bias parameter (1 − b). All the other parameters are sampled with the priors listed in Table A.1. In one particular case, that is to reproduce the results of Reichardt et al. (2021), all cosmological parameters are fixed to the fiducial values shown in the same table.
4. Results
We use our modified version of CosmoMC, including the Planck21-tSZ and the SPT high-ℓ likelihoods, to sample cosmological and scaling relation parameters and study the impact of updating the tSZ computation from an amplitude and a template to a physically motivated model.
4.1. Impact of the RF-reconstructed tSZ power spectrum
As a first step in our analysis, we validate our machine-learning technique at the cosmological inference level. We compare the results of running CosmoMC with a full computation of the tSZ Cℓ’s, and with the RF-inferred ones. We compare in Fig. 2 the contours obtained in a MCMC run using our Planck-tSZ likelihood and varying two cosmological parameters (Ωm and σ8) and two scaling relation parameters, α (with a prior) and (1 − b). Results from the two approaches are fully in agreement. Therefore, in the rest of this work, we rely on the RF-inferred Cℓ’s instead of the full derivation when using our analytical tSZ power spectra. They are referred throughout as ‘RF tSZ’ power spectra.
 |
Fig. 2. Comparison of MCMC runs with ‘true’ Cℓ’s and RF Cℓ’s for cosmological and scaling relation parameters. In grey, both Cℓ’s and the non-Gaussian contribution (σTℓℓ′) are computed as detailed in Sect. 2.1. In blue, σTℓℓ′ is approximated by a constant value over ℓ and cosmology. In orange, the Cℓ’s are computed with the RF and the sample variance noise is approximated by a constant. |
To further speed up the calculation, we also approximate the noise part coming from the full connected trispectrum by a constant term, as discussed in Sect. 3.2.
We report the results for the RF tSZ power spectrum with the constant trispectrum term in Fig. 2, and show that the approximation is consistent with the full evaluation. Since the trispectrum term becomes negligible at multipoles higher than 2000, the range covered by the SPT data, this approximation will hold even better in the SPT analysis
4.2. Impact on cosmological parameters
We now study the consequences of substituting the tSZ template with cosmology-dependent spectra. We fitted the SPT data, letting the five cosmological parameters free with only priors on ns and Ωbh2. We assume priors on the tSZ parameters α and log Y*, but leave the mass bias free to vary. Indeed, as shown in previous tSZ studies (Planck Collaboration XXI 2014; Horowitz & Seljak 2017; Salvati et al. 2018; Bolliet et al. 2018), the cosmological parameters and the mass bias are degenerate, so that fixing the mass bias will be equivalent to setting a prior on the cosmological parameters. The priors used are listed in Table A.1. In practice, we have one more degree of freedom compared to Reichardt et al. (2021): α and (1 − b) are added to describe the tSZ signal, whilst the amplitude parameter AtSZ at ℓ = 3000 is removed. In total, including foregrounds and SPT instrumental parameters, we have 22 free parameters. Nevertheless, as the shape of the tSZ power spectrum is now fitted to the SPT data, the constraints on cosmological parameters improve: Fig. 3 compares the posterior distributions of H0, Ωm and σ8 obtained with the template and with the RF. We can see that using SPT data alone with the tSZ template (in grey) allows for a large range of parameter values, including a narrow degeneracy between H0 and Ωm. These constraints are driven by the CMB spectrum dominating other signals on the range 2000 < ℓ < 4000 but being negligible at smaller scales. As expected, substituting the template by our RF tSZ power spectrum (blue contours) allows one to exploit the full cosmological information, and the constraints are largely tightened with a factor of about two in improvement (see Table 1).
 |
Fig. 3. Constraints on cosmological parameters obtained with SPT high-ℓ data using the tSZ template as done in Reichardt et al. (2021, in grey) and using the tSZ power spectra derived from the halo model (in blue). |
Constraints on cosmological and mass bias parameters for the different dataset combinations.
Figure 4 shows the best-fit spectra for the data at 95 × 150 GHz in the two scenarios (dashed lines for template, and solid line for RF), plotted as Dℓ = ℓ(ℓ + 1)Cℓ/2π. One can see the difference in amplitude and shape of the two tSZ spectra. Results for all SPT frequency bands and cross-spectra are shown in Appendix B. Relative amplitudes of tSZ and kSZ are discussed in Sect. 4.4.
 |
Fig. 4. Best-fit spectra of SPT data for the 95 × 150 GHz bandpower (black data points) for CMB, tSZ and other foregrounds when using RF (solid lines) or a template (dashed lines) to derive the tSZ contribution. |
4.3. Combining Planck tSZ power spectrum and SPT data
In the following, we combine the Planck21-tSZ power spectrum at large scales (60 < ℓ < 1400) with the SPT data at small scales (ℓ > 2000), described in Sect. 3. We consider the case with RF power spectrum only, and compare with results for SPT data alone in Fig. 5. Adding the Planck21-tSZ data (in red) only slightly tightens the constraints but moves the best-fit towards smaller values for Ωm and σ8 by roughly 1σ. These values are in better agreement with the Planck CMB constraints, within 1σ (Planck Collaboration I 2020).
 |
Fig. 5. Constraints on cosmological and scaling relation parameters using different data sets and priors: in blue, SPT high-ℓ data alone, and in red, with Planck21-tSZ power spectra added. Results when CCCP prior on the mass bias is added are shown in green. |
The most likely value for the mass bias (1 − b) similarly shifts towards a higher value when adding the Planck21-tSZ data, now in better agreement with the combination of Planck CMB and Planck SZ cluster counts (Salvati et al. 2018), but lower than most hydrostatic mass bias estimates (see Douspis et al. 2018; Gianfagna et al. 2021 for compilations). Adding a prior on the mass bias from the Canadian Cluster Comparison Project (CCCP, Hoekstra et al. 2015) breaks the degeneracy between cosmological and scaling relation parameters, and eliminates high values of Ωm and σ8 (in green on Fig. 5). All results are reported in Table 1. Figure 6 shows the tSZ power spectrum estimates of SPT at 95 × 150 GHz once other foregrounds and primordial CMB are removed, as well as of Planck21-tSZ estimates renormalised at the same frequency, along with our best-fit result.
 |
Fig. 6. Best-fit SZ spectra of SPT (in orange) and Planck21-tSZ (in blue) data, foregrounds removed, at 95 × 150 GHz, when both of them are fitted simultaneously. The grey bands show the 1 and 2σ uncertainty on the best model. Similar plot for all cross spectra are shown in Appendix C. |
These 1-σ best-fit changes shown in Fig. 5 illustrate that the exact value of the best-fit depends on the assumptions on the foregrounds and calls for a more coherent analysis of large and small scale data, primordial and secondary anisotropies.
4.4. Impact on kSZ detection
Reichardt et al. (2021) have set constraints on the amplitude of the kSZ effect in SPT high-ℓ data, finding a 3-σ detection when fixing the cosmology. The authors find that changing the templates used for the tSZ and kSZ power spectra makes the significance of their results range between 2.4 and 3-σ. We compare results on the kSZ power amplitude  in the different cases considered above, that is with fixed or free cosmology, with Gaussian or uniform priors on the cluster parameters. Figure 7 shows the one-dimensional likelihood on the kSZ amplitude for all cases, as well as the degeneracy between kSZ and tSZ amplitudes4 at ℓ = 3000. The default analysis by Reichardt et al. (2021), using tSZ and kSZ templates, in black, gives the highest kSZ amplitude with the highest significance. Allowing, within the same set-up, cosmological parameters to vary5 lowers the value of
in the different cases considered above, that is with fixed or free cosmology, with Gaussian or uniform priors on the cluster parameters. Figure 7 shows the one-dimensional likelihood on the kSZ amplitude for all cases, as well as the degeneracy between kSZ and tSZ amplitudes4 at ℓ = 3000. The default analysis by Reichardt et al. (2021), using tSZ and kSZ templates, in black, gives the highest kSZ amplitude with the highest significance. Allowing, within the same set-up, cosmological parameters to vary5 lowers the value of  by about 1σ (in grey). Substituting the template with the RF tSZ power spectrum leads to different results than Reichardt et al. (2021). Using the RF and freeing the cosmology allows the shape of the tSZ spectrum to change and thus better fit the details of the data. As a consequence, the kSZ amplitude and detection significance decrease drastically (in blue). The corresponding tSZ and kSZ spectra are shown in both scenarios in Fig. 4, for the 95 × 150 GHz data. Finally, adding Planck tSZ data and prior on the mass bias moves the constraints by less than 1σ (in red and green, respectively).
by about 1σ (in grey). Substituting the template with the RF tSZ power spectrum leads to different results than Reichardt et al. (2021). Using the RF and freeing the cosmology allows the shape of the tSZ spectrum to change and thus better fit the details of the data. As a consequence, the kSZ amplitude and detection significance decrease drastically (in blue). The corresponding tSZ and kSZ spectra are shown in both scenarios in Fig. 4, for the 95 × 150 GHz data. Finally, adding Planck tSZ data and prior on the mass bias moves the constraints by less than 1σ (in red and green, respectively).
 |
Fig. 7. Constraints on the amplitude of the tSZ and kSZ power spectra at ℓ = 3000 and 143 GHz, using different data sets and methods to account for the tSZ signal. In grey and black are shown results obtained when using templates Reichardt et al. (2021), with and without varying cosmology, respectively. Other colours refer to results using the halo model to derive the tSZ power and freeing cosmology. In blue, only SPT data is considered. In green and red, Planck21-tSZ data is added, with Gaussian and uniform prior on the bias parameter, respectively. |
These results show the sensitivity of the detection of kSZ effect to the assumptions made on other foregrounds or on the cosmological model used in the analysis. They motivate a similar treatment of other foregrounds such as the kSZ power spectrum and the CIB to ensure a robust detection of both SZ signals. The former is the subject of a companion paper (Gorce et al. 2022), focusing on kSZ and reionisation history.
5. Conclusions
Small-scale millimetre wavelength signals encompass a wealth of cosmological information. Several studies have used such information independently, focusing on the derived tSZ spectrum from y-maps (Planck Collaboration XXI 2014; Planck Collaboration XXII 2016; Salvati et al. 2018; Bolliet et al. 2018), the kSZ amplitude (Zahn et al. 2012; Planck Collaboration XLVII 2016; Reichardt et al. 2021) or the measured CIB spectrum (Planck Collaboration XXX 2014; Maniyar et al. 2021). In contrast, in our framework, information is extracted from all cosmological signals at small scales simultaneously and coherently.
In this first work, we focus on the tSZ power spectrum and how, in combination with CMB observations at small scales, it can help constraining cosmological parameters. Instead of assuming a fixed template shape and a free amplitude, we compute the tSZ angular power spectrum from the halo model from a set of cosmological and scaling relation parameters. However, this derivation is computationally intensive and we choose to train a Random Forest (RF) on 15 000 of tSZ angular power spectra and use the resulting predictions, accurate at more than the 2% level, in a full Markov chain Monte Carlo analysis of the SPT high-ℓ data6 (Reichardt et al. 2021). Considering the width of current error bars on small-scale measurements of the CMB power spectrum and the modelling uncertainties of other CMB foregrounds, such an accuracy level is sufficient, but will need to be improved once data from the next generation of CMB observatories is available. We improve the constraints on Ωm, H0 and σ8 by a factor of six compared to the case neglecting tSZ cosmological information, considering the figure of merit FOM = 1/(σH0σΩmσσ8). This represents the first step towards using the full potential of small-scale CMB data. We then combine the SPT high-ℓ data with the Planck21-tSZ power spectrum (Tanimura et al. 2022) to further constrain cosmological and scaling relation parameters. This combination does improve constraints but mostly shifts the best-fit parameters towards smaller values of Ωm, and σ8 (from 0.38 and 0.82 to 0.35 and 0.77, respectively), in better agreement with Planck CMB data. Adding a prior on the mass bias parameter from CCCP tightens the constraints on the three cosmological parameters of interest by another factor of six and brings the best-fit towards those of other tSZ analyses for a value of S8 ≡ σ8(Ωm/0.3)0.5 = 0.76 ± 0.04, while remaining compatible with Planck CMB results (Planck Collaboration VI 2020). Conversely, combining high-ℓ and tSZ data with large-scale CMB (Planck Collaboration VI 2020) or future small-scale experiments (Benson et al. 2014; Xu et al. 2021; Carlstrom et al. 2019, respectively SPT3G, Simons Observatory and CMB-S4) will constrain the cosmological model strongly and, in turn, the scaling parameters. Such constraints on a mean scaling relation, averaged over all masses and all redshifts, would need to be compared with most recent estimates using large samples of clusters in X-ray (Ricci et al. 2020; Lovisari et al. 2020; Predehl et al. 2021; Chiu et al. 2021) or in optical (Sartoris et al. 2016; Salvati et al. 2020; Schrabback et al. 2021; Eifler et al. 2021). We choose to limit ourselves to qualitative comparisons. Indeed, we expect constraints to change once the cosmological dependence of other foregrounds, such as the kSZ and the CIB, as well as large-scale data, are included in the analysis.
Finally, we investigate the amplitude of the deduced kSZ contribution and the amplitude of the tSZ effect on small scales (ℓ = 3000). When compared with the original study by Reichardt et al. (2021), which fixed cosmological parameters and used templates for all small-scale foregrounds, this new analysis leads to a lower contribution of the kSZ to the overall observed power. Its amplitude is still detected but with decreased significance  K2. A more careful analysis, also including the cosmological dependency of the kSZ and CIB effects, needs to be performed to obtain a more robust estimate of the contribution of the kSZ effect to small-scale CMB data and its implications in terms of the Epoch of Reionisation. This is the focus of a forthcoming companion paper (Douspis et al., in prep.).
K2. A more careful analysis, also including the cosmological dependency of the kSZ and CIB effects, needs to be performed to obtain a more robust estimate of the contribution of the kSZ effect to small-scale CMB data and its implications in terms of the Epoch of Reionisation. This is the focus of a forthcoming companion paper (Douspis et al., in prep.).
Whilst more complete and coherent, our analysis is based on a model giving the tSZ power spectrum from a set of parameters and is, therefore, limited by the physical assumptions made for modelling the astrophysical contributions to the small-scale power. These limitations should be overcome, and the accuracy of the RF prediction improved, once data from future surveys – or their combination, with enough sensitivity to constrain both cosmological and astrophysical parameters simultaneously, is available.
The priors on ns and Ωbh2 presented in Table A.1 are used.
The RF prediction code for tSZ power spectra will be made publicly available once this article is published. It may also be shared upon reasonable request to the authors and see https://szdb.osups.universite-paris-saclay.fr/.
Acknowledgments
The authors acknowledge the SPT collaboration and C. Reichardt for making the SPT data and likelihood available online (likelihoods, figures and data points from Reichardt et al. 2021 are available at https://pole.uchicago.edu/public/data/reichardt20/). AG’s work was supported by the McGill Astrophysics Fellowship funded by the Trottier Chair in Astrophysics, as well as the Canadian Institute for Advanced Research (CIFAR) Azrieli Global Scholars program and the Canada 150 Programme. N.A. is partly funded by the ByoPiC project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme grant agreement ERC-2015-AdG 695561. The authors acknowledge fruitful discussions with the members of the ByoPiC project (https://byopic.eu/team). This research made use of the computation facility of IDOC (http://idoc.ias.u-psud.fr), partly provided by DIM ACAV (http://www.dimacav-plus.fr). This research made use of matplotlib, a Python library for publication quality graphics (Hunter 2007), Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), of scipy, a Python-based ecosystem of open-source software for mathematics, science, and engineering (Jones et al. 2001) – including numpy (Van Der Walt et al. 2011), and of scikit-learn (Pedregosa et al. 2011).
References
- Aghanim, N., Desert, F. X., Puget, J. L., & Gispert, R. 1996, A&A, 311, 1 [NASA ADS] [Google Scholar]
- Aghanim, N., Douspis, M., Hurier, G., et al. 2019, A&A, 632, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benson, B. A., Ade, P. A. R., Ahmed, Z., et al. 2014, in Millimeter, Submillimeter, and Far-infrared Detectors and Instrumentation for Astronomy VII, eds. W. S. Holland, & J. Zmuidzinas, SPIE Conf. Ser., 9153, 91531P [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., Crawford, T. M., Ansarinejad, B., et al. 2022, ApJ, DOI:https://doi.org/10.3847/1538-4365/ac35e9 [Google Scholar]
- Bolliet, B., Comis, B., Komatsu, E., & Macías-Pérez, J. F. 2018, MNRAS, 477, 4957 [NASA ADS] [CrossRef] [Google Scholar]
- Bonjean, V., Aghanim, N., Salomé, P., et al. 2019, A&A, 622, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlstrom, J., Abazajian, K., Addison, G., et al. 2019, BAAS, 51, 209 [Google Scholar]
- Chiu, I. N., Ghirardini, V., Liu, A., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202141755 [Google Scholar]
- Cooray, A. 2000, Phys. Rev. D, 62, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Couchot, F., Henrot-Versillé, S., Perdereau, O., et al. 2017, A&A, 597, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douspis, M., Salvati, L., & Aghanim, N. 2018, Exploring the Dark Side of the Universe, 37 [Google Scholar]
- Eifler, T., Miyatake, H., Krause, E., et al. 2021, MNRAS, 507, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- George, E. M., Reichardt, C. L., Aird, K. A., et al. 2015, ApJ, 799, 177 [Google Scholar]
- Gianfagna, G., De Petris, M., Yepes, G., et al. 2021, MNRAS, 502, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Gorce, A., Ilić, S., Douspis, M., Aubert, D., & Langer, M. 2020, A&A, 640, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorce, A., Douspis, M., & Salvati, L. 2022, ArXiv e-print [arXiv:2202.08698] [Google Scholar]
- Han, D., Sehgal, N., MacInnis, A., et al. 2021, JCAP, 2021, 031 [CrossRef] [Google Scholar]
- Hernandez Vivanco, F., Smith, R., Thrane, E., & Lasky, P. D. 2020, MNRAS, 499, 5972 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, B., & Seljak, U. 2017, MNRAS, 469, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., & Lacasa, F. 2017, A&A, 604, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Kennedy, A., Nash, G., Rattenbury, N. J., & Kempa-Liehr, A. W. 2021, Astron. Comput., 35, 100460 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., & Kitayama, T. 1999, ApJ, 526, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., & Seljak, U. 2002, MNRAS, 336, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A. 2013, Phys. Rev. D, 87, 103529 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [Google Scholar]
- Lovisari, L., Schellenberger, G., Sereno, M., et al. 2020, ApJ, 892, 102 [Google Scholar]
- Madhavacheril, M. S., Hill, J. C., Næss, S., et al. 2020, Phys. Rev. D, 102, 023534 [Google Scholar]
- Maniyar, A., Béthermin, M., & Lagache, G. 2021, A&A, 645, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Planck Collaboration XXI. 2014, A&A, 571, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XLVII. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration LVII. 2020, A&A, 643, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Patil, S., Ade, P. A. R., et al. 2021, ApJ, 908, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, M., Adam, R., Eckert, D., et al. 2020, A&A, 642, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2020, A&A, 643, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sartoris, B., Biviano, A., Fedeli, C., et al. 2016, MNRAS, 459, 1764 [Google Scholar]
- Schaan, E., Ferraro, S., Amodeo, S., et al. 2021, Phys. Rev. D, 103, 063513 [NASA ADS] [CrossRef] [Google Scholar]
- Schrabback, T., Bocquet, S., Sommer, M., et al. 2021, MNRAS, 505, 3923 [NASA ADS] [CrossRef] [Google Scholar]
- Spurio Mancini, A., Piras, D., Alsing, J., Joachimi, B., & Hobson, M. P. 2022, MNRAS, 511, 1771 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, I. B. 1980, ARA&A, 18, 537 [Google Scholar]
- Tanimura, H., Douspis, M., Aghanim, N., & Salvati, L. 2022, MNRAS, 509, 300 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Xu, Z., Adachi, S., Ade, P., et al. 2021, Res. Notes Am. Astron. Soc., 5, 100 [Google Scholar]
- Zahn, O., Zaldarriaga, M., Hernquist, L., & McQuinn, M. 2005, ApJ, 630, 657 [Google Scholar]
- Zahn, O., Reichardt, C. L., Shaw, L., et al. 2012, ApJ, 756, 65 [Google Scholar]
- Zeldovich, Y. B., & Sunyaev, R. A. 1969, Astrophys. Space Sci., 4, 301 [Google Scholar]
Appendix A: Parameters
Table A.1 lists all parameters, cosmological and scaling relation, related to the tSZ spectrum, along with their definitions, values when fixed, and applied priors.
Definition, symbol, prior and ranges assumed for considered parameters. ‘SR’ stands for scaling relation.
Appendix B: Best-fit spectra at different frequencies
We reproduce here Fig. 4 but with a different colourmap and for all combinations of frequencies allowed by the data, that is auto-spectra at 95, 150 and 220 GHz, and cross-spectra at 95 × 150, 95 × 220 and 150 × 220 GHz.
 |
Fig. B.1. Best-fit spectra of SPT data for CMB, tSZ and other foregrounds, as well as the sum of all compared with the SPT data at different frequencies. We compare results when templates or RF predictions are used to obtain the tSZ power spectrum. |
Appendix C: Best-fit SZ spectra estimates for all (cross) frequencies
We reproduce here Fig. 6 for all combinations of frequencies allowed by the SPT data, that is auto-spectra at 95, 150 and 220 GHz, and cross-spectra at 95 × 150, 95 × 220 and 150 × 220 GHz.
All Tables
Constraints on cosmological and mass bias parameters for the different dataset combinations.
Definition, symbol, prior and ranges assumed for considered parameters. ‘SR’ stands for scaling relation.
All Figures
 |
Fig. 1. Comparison of the ‘true’ tSZ Cℓ’s values at given ℓ (crosses, and solid lines) with the RF-inferred Cℓ’s after interpolation (dashed lines) for a sample of models (units are arbitrary before renormalisation in y-units at 143 GHz). The lower part of the plot shows the ratio of RF Cℓ’s over ‘true’ Cℓ’s. The grey areas are showing the 68% and 95% dispersion among the test set. |
| In the text | |
 |
Fig. 2. Comparison of MCMC runs with ‘true’ Cℓ’s and RF Cℓ’s for cosmological and scaling relation parameters. In grey, both Cℓ’s and the non-Gaussian contribution (σTℓℓ′) are computed as detailed in Sect. 2.1. In blue, σTℓℓ′ is approximated by a constant value over ℓ and cosmology. In orange, the Cℓ’s are computed with the RF and the sample variance noise is approximated by a constant. |
| In the text | |
 |
Fig. 3. Constraints on cosmological parameters obtained with SPT high-ℓ data using the tSZ template as done in Reichardt et al. (2021, in grey) and using the tSZ power spectra derived from the halo model (in blue). |
| In the text | |
 |
Fig. 4. Best-fit spectra of SPT data for the 95 × 150 GHz bandpower (black data points) for CMB, tSZ and other foregrounds when using RF (solid lines) or a template (dashed lines) to derive the tSZ contribution. |
| In the text | |
 |
Fig. 5. Constraints on cosmological and scaling relation parameters using different data sets and priors: in blue, SPT high-ℓ data alone, and in red, with Planck21-tSZ power spectra added. Results when CCCP prior on the mass bias is added are shown in green. |
| In the text | |
 |
Fig. 6. Best-fit SZ spectra of SPT (in orange) and Planck21-tSZ (in blue) data, foregrounds removed, at 95 × 150 GHz, when both of them are fitted simultaneously. The grey bands show the 1 and 2σ uncertainty on the best model. Similar plot for all cross spectra are shown in Appendix C. |
| In the text | |
 |
Fig. 7. Constraints on the amplitude of the tSZ and kSZ power spectra at ℓ = 3000 and 143 GHz, using different data sets and methods to account for the tSZ signal. In grey and black are shown results obtained when using templates Reichardt et al. (2021), with and without varying cosmology, respectively. Other colours refer to results using the halo model to derive the tSZ power and freeing cosmology. In blue, only SPT data is considered. In green and red, Planck21-tSZ data is added, with Gaussian and uniform prior on the bias parameter, respectively. |
| In the text | |
 |
Fig. B.1. Best-fit spectra of SPT data for CMB, tSZ and other foregrounds, as well as the sum of all compared with the SPT data at different frequencies. We compare results when templates or RF predictions are used to obtain the tSZ power spectrum. |
| In the text | |
 |
Fig. C.1. Same as Fig. 6 but at different frequencies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



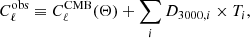




![$$ \begin{aligned} C_{\ell }^{2\mathrm{halo}} =&\int _0^{z_{\rm max}} \mathrm{d}z \, \dfrac{\mathrm{d}V}{\mathrm{d}z\,\mathrm{d}\Omega }\nonumber \\&\times \left[\int _{M_{\rm min}}^{M_{\rm max}} \mathrm{d}M \, \dfrac{\mathrm{d}n(M_{500,z})}{\mathrm{d}M_{500}} \, \tilde{{ y}}_{\ell } (M_{500},z) \, B(M_{500},z)\right]^2\nonumber \\&\times P(k,z). \end{aligned} $$](/articles/aa/full_html/2022/03/aa42004-21/aa42004-21-eq9.gif)



![$$ \begin{aligned} E^{-\beta }(z) \left[\dfrac{D_{\rm A}(z)^2 Y_{500}}{10^{-4}\,\mathrm{Mpc}^2}\right] = Y_\star \left[\dfrac{h}{0.7}\right]^{-2+\alpha } \left[\dfrac{(1-b) M_{500}}{6 \times 10^{14}\,M_{\odot }}\right]^{\alpha }, \end{aligned} $$](/articles/aa/full_html/2022/03/aa42004-21/aa42004-21-eq14.gif)





