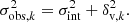EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 662 (June 2022) A&A, 662 (2022) A57 Full HTML
Open Access
Issue
A&A
Volume 662, June 2022
Article Number A57
Number of page(s) 7
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202142351
Published online 14 June 2022

© O. Müller et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Galaxy groups are a key testbed for the Λ cold dark matter (ΛCDM) cosmological model (Kroupa et al. 2010; Bullock & Boylan-Kolchin 2017; Oppenheimer et al. 2021) as well as for alternative theories (Banik & Zhao 2018; Milgrom 2019). In the Local Volume (D <  11 Mpc), about half of all major galaxies reside in virialized groups, while the remaining half constitutes the so-called field population (Karachentsev 2005). More massive galaxy clusters, which are absent in the Local Volume, are estimated to contain a minor fraction of the galaxy population, about 10%−15% (Karachentsev 2005). Unfortunately, estimating the dynamical mass (Mdyn) of galaxy groups is more challenging than for galaxy clusters. Only a subsample of galaxy groups have a high-density hot medium that can be studied with existing X-ray telescopes to estimate Mdyn from hydrostatic equilibrium (e.g., see Kourkchi & Tully 2017 and references therein). Moreover, galaxy groups are too diffuse to produce a detectable gravitational lensing signal from background galaxies. The only remaining approach is to use the line-of-sight velocities of galaxy members, as it was pioneered by Zwicky (1933) almost a century ago.

Dynamical mass estimates for galaxy groups usually rely on the fvirial theorem and/or on the “zero-velocity surface” method (Lynden-Bell 1981; Sandage 1986; Karachentsev 2005; Karachentsev et al. 2009; Tully 2015; Kashibadze & Karachentsev 2018). Both methods assume that the member galaxies are isotropically distributed (spherical symmetry) and follow random orbits. These assumptions appear unreasonable for our own Local Group: most dwarf satellites of the Milky Way and M31 are distributed in narrow planar structures with significant angular momentum (Pawlowski et al. 2012; Ibata et al. 2013; Pawlowski & Kroupa 2020; Santos-Santos et al. 2020; Pawlowski & Tony Sohn 2021). Flattened distributions of galaxies are also observed on larger spatial scales out to 1 − 2 Mpc in the Local Group (Pawlowski et al. 2013) and in other nearby groups (Müller et al. 2017; Byun et al. 2020; Heesters et al. 2021; Martínez-Delgado et al. 2021). Thus, it is important to check the accuracy of these methods by comparing them with different approaches to estimate Mdyn.

The Centaurus group is one of the best studied galaxy systems in our cosmic neighborhood (e.g., Côté et al. 1997; Jerjen et al. 2000a; Karachentsev et al. 2002; Crnojević et al. 2011; Müller et al. 2015; Taylor et al. 2018). Similarly to the Local Group, it is composed of two main giant galaxies – Centaurus A (Cen A) and M83 – each one with its own system of dwarf satellite galaxies. In this article we focus on Cen A and its dwarf galaxy satellites, which we refer to as the “Cen A group” for simplicity.

The combination of accurate distances based on the tip of the red giant branch (TRGB) method and line-of-sight velocity measurements for 28 dwarf galaxies show that the Cen A satellite system forms a flattened and kinematically coherent structure (Tully et al. 2015; Müller et al. 2016, 2018, 2021a), analogous to those found around the Milky Way and M31. Satellite systems with a similar kinematic coherence are extremely rare in ΛCDM simulations, leading to the so-called planes of satellites problem (Kroupa et al. 2010; Libeskind et al. 2015; Pawlowski 2018). These observations also suggest that dynamical mass estimates of Cen A should consider a flattened (non-spherical) system with both rotation and pressure support.

In this article, we use a Bayesian model to show that the satellite system of Cen A has significant rotational support (Sect. 2). Next, we use the Jeans’ equation in cylindrical symmetry to estimate the circular velocity and dynamical mass of the Cen A group (Sect. 3). Finally, we compare our new mass estimate with previous determinations in the literature and discuss the implications for ΛCDM cosmology and alternative theories (Sect. 4).

2. Kinematics of Cen A satellite system

Cen A has 42 confirmed satellites and 30 additional candidates that await membership confirmation (Müller et al. 2019). Here we consider 27 galaxies from Müller et al. (2021a) that have both TRGB distances and line-of-sight velocities (see their Table A.1)1, as well as one dwarf galaxy with only velocity information, giving a total of 28 dwarf galaxies. For three galaxies, the EDD team2 (Tully et al. 2009) has re-reduced and updated the available HI data. The new values for the line-of-sight velocities are 468 ± 2 km s−1 for NGC 5102, 516 ± 3 km s−1 for ESO 324-024, and 545 ± 2 km s−1 for ESO 325-011, which we adopt here. Throughout the paper, based on EDD, we adopt a distance of 3.68 Mpc for Cen A; we note, however, that an average distance of 3.8 ± 0.1 Mpc for Cen A was found using different distance estimates (Rejkuba 2004; Harris et al. 2010). We used the EDD value to be as self-consistent as possible.

We built a Bayesian model to quantify the relative degrees of rotation and pressure support in the satellite system. Similar models have been used to study the motion of globular clusters within their host galaxies (e.g., Côté et al. 2001; Veljanoski & Helmi 2016; Fahrion et al. 2020a; Lewis et al. 2020). Our model assumes that the satellite system is centered on Cen A and that its galaxy members rotate in a common plane with a mean velocity vrot. Deviations from purely circular motions (out-of-planar motions and more complex orbits) are encapsulated in the parameter σint that is a proxy for the mean velocity dispersion of the satellite system. This parameter sums quadratically to the observational error δv, k on the line-of-sight velocity vobs,k of a satellite k, giving the observed deviation from purely circular motions:

σ obs , k 2 = σ int 2 + δ v , k 2 . $$ \begin{aligned} \sigma _{\mathrm{obs}, k}^2 =\sigma _{\rm int}^2+\delta _{\mathrm{v},k}^2. \end{aligned} $$(1)

The projected velocity of a satellite galaxy along the line of sight is then given by

v mod ( v rot , i , PA ) = v rot sin ( i ) − Δ RA , k sin ( PA ) + Δ Dec , k cos ( PA ) D 3 D , k , $$ \begin{aligned} {v}_{\rm mod}({v}_{\rm rot}, i, \mathrm{PA}) ={v}_{\rm rot} \sin {({i})} \frac{-\Delta _{\mathrm{RA}, k} \sin {(\mathrm{PA})} + \Delta _{\mathrm{Dec}, k}\cos {(\mathrm{PA})}}{ {D_{\mathrm{3D,} k}}}, \end{aligned} $$(2)

where i is the inclination of the plane with respect to the sky, PA is the position angle of the major axis of the plane, D3D, k is the measured 3D distance of a satellite k from Cen A, and ΔRA, k and ΔDec, k are its projected separations from Cen A in the right ascension and declination directions, respectively.

The log likelihood is then given by the following:

log L = ∑ k = 1 N log ( 1 2 π σ obs ) − ( v obs , k − ( v mod + v sys ) ) 2 2 σ obs , k 2 , $$ \begin{aligned} \log \mathcal{L} =\sum _{\rm k=1}^N{\log \left(\frac{1}{\sqrt{2\pi } \sigma _{\rm obs}}\right) -\frac{\left({v}_{{\mathrm{obs}, k}}-({v}_{\rm mod}+{v}_{\rm sys})\right)^2}{2\sigma _{\mathrm{obs}, k}^2}}, \end{aligned} $$(3)

where N = 28 is the number of satellites and vsys is the systemic velocity of the satellite system. Thus, the free parameters of the model are vrot, σint, PA, i, and vsys.

For the systemic velocity, we assume a Gaussian prior centered at 556 km s−1 (the mean of vobs, k) with a standard deviation of 10 km s−1 (the standard error on the mean). The central value of vsys is in close agreement with the systemic velocity of Cen A from HI observations (Koribalski et al. 2004), planetary nebulae (Peng et al. 2004a), and globular clusters (Peng et al. 2004b; Woodley et al. 2010)3. For the inclination angle, we assume a Gaussian prior centered at 86° with a standard deviation of 1° as suggested by the 3D geometry of the satellite system (Müller et al. 2019). In general, the rotation velocity of a projected disk is degenerate with the inclination angle: a tight prior on i is crucial to break this degeneracy. Given that the satellite plane is seen close to edge-on, the precise value of i plays a minor role in our estimate of vrot (see Eq. (2)).

For the position angle, we ran a preliminary Markov chain Monte Carlo (MCMC) simulation using a flat prior with 0° < PA <  360°. The resulting posterior probability distribution marginalized along PA displays two nearly Gaussian modes separated by ∼180°, which represents two physical solutions for clockwise and anticlockwise rotation. We shifted one of the modes by 180° and determined PA = 63.7° ±37.9°, which we used to set a Gaussian prior on PA in a final MCMC run. For σint and vrot, we used broad flat priors with 0 <  σint <  300 km s−1 and −400 <  vrot <  400 km s−1. To sample the posterior distribution, we ran a MCMC with 100 walkers with a chain length of 10’000 each. We used 100 burn-in iterations and then sampled over the full chains to get the posterior.

Figure 1 shows that the posterior distributions are well behaved and display distinct peaks, indicating that the maximum-likelihood parameters are well determined. We found a rotational component with vrot = 90 ± 49 km s−1 (∼2σ detection) and a random component with σ int = 124 − 15 + 20 $ \sigma_{\mathrm{int}}=124^{+20}_{-15} $ km s−1 (∼7σ detection). The resulting vrot/σint ratio is ∼0.7 − 0.42 + 0.57 $ ^{+0.57}_{-0.42} $, indicating that rotational support is non-negligible. To test the significance of the rotational component, we re-ran our experiment 100 times by reshuffling the velocities and their errors among the satellites (all other parameters were kept the same). This results in a lower rotational component (9 ± 47 km s−1) and a higher random component (130 ± 5 km s−1). Most likely, the satellite system forms a thick structure flattened by rotation (see also Müller et al. 2019). 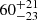The final PA value of 60 − 23 + 21 $ 60^{+21}_{-23} $ degrees is consistent with previous estimate within ∼2.5σ (Müller et al. 2018, 2021a); the difference is due to the fact that the current measurement maximizes the rotation signal, while previous measurements maximized the number of kinematically coherent satellites considering only the sign of the line-of-sight velocities vobs, k with respect to Cen A, but not their absolute values. Our results for σint and vrot are consistent with those from Woodley (2006), who found σint = 115± 25 km s−1, vrot = 125 ± 50 km s−1, and PA = 159 ± 23° using a spherical model for a smaller sample of 13 galaxies. The PA estimates differ significantly, though.

thumbnail Fig. 1.

Posterior distribution of the five fitting parameters from the MCMC analysis of the Cen A satellite system. In the histograms, the three dashed lines indicate the 16, 50, and 84 percentiles, which correspond to the upper and lower uncertainty boundaries, and the best-fit parameter estimation (i.e., the median). See Sect. 2 for details.

Figure 2 shows a position-velocity (PV) diagram along the projected major axis of the kinematic plane. The contours represent a rotating disk model projected on the sky, using the best-fit parameters from the MCMC analysis (Fig. 1). The disk model has a Gaussian thickness of 130 kpc (Müller et al. 2019) and assumes that satellite galaxies have an equal probability of being found at any radius in the plane. Then, when the disk is projected to a nearly edge-on orientation (i = 86°), the probability of having a galaxy at small projected distances is higher than having one at larger projected distances due to the line-of-sight integration. Figure 2 shows that all galaxies but one – KK 203 – agree within 2σ with our model (∼60% within 1σ).

thumbnail Fig. 2.

Position-velocity diagram along the projected major axis of the satellite system. Red dots with 1σ error bars show satellites of Cen A with measured line-of-sight velocities. The contours represent the best-fit rotating disk model with vrot = 90 km s−1 and σint = 124 km s−1. The inner and outer contours correspond to 1σ and 2σ probabilities of finding a galaxy at that location of the position-velocity diagram.

3. Dynamics of Cen A satellite system

3.1. Mean circular velocity

We used the motion of satellite galaxies around Cen A to measure the circular velocity and dynamical mass of the whole group. A dynamical analysis is not straightforward because the satellite system is supported by both rotation and random motions and only line-of-sight velocities are available. We assumed that the satellite system is axisymmetric and adopted a cylindrical reference system (R, z, ϕ) where z is perpendicular to the rotating plane defined by Eq. (2). We further assumed that the velocity ellipsoid is isotropic ( σ R 2 = σ z 2 = σ ϕ 2 $ \sigma_{\rm R}^2 = \sigma_{\rm z}^2 = \sigma_{\phi}^2 $), and thus the parameter σint in our MCMC analysis can be equated to the isotropic velocity dispersion. Under these simplifying assumptions, the circular velocity of a test particle subjected to the equilibrium gravitational potential is given by the Jeans’ equation in cylindrical symmetry (see, e.g., Lelli et al. 2014):

v circ 2 ( R ) = v rot 2 ( R ) − A ( R ) × σ int 2 ( R ) , $$ \begin{aligned} {v}_{\rm circ}^2(R) = {v}_{\rm rot}^2(R)- A(R) \times \sigma _{\rm int}^2(R), \end{aligned} $$(4)

where

A ( R ) = ∂ ln ρ ( R ) ∂ ln R + 2 ∂ ln σ int ( R ) ∂ ln R $$ \begin{aligned} A(R)= \frac{\partial \ln \rho (R)}{\partial \ln R}+2\frac{\partial \ln \sigma _{\rm int}(R)}{\partial \ln R} \end{aligned} $$(5)

depends on the density profile of the tracers ρ(R) and the velocity dispersion profile σint(R). Having only 28 galaxies with line-of-sight velocities, we could not constrain the velocity dispersion profile, so we considered σint as the average velocity dispersion across different radii and set the second term in Eq. (5) to zero.

To estimate the first term in Eq. (5), we considered all confirmed Cen A members adding 15 galaxies with known distances4 (but without line-of-sight velocities) for a total of 43 objects. We projected the galaxies in the plane (R, ϕ) integrating along z, that is a face-on projection of the satellite system. We assumed that the thickness of the plane does not change with radius, so ∂lnρ/∂lnR = ∂lnΣ/∂lnR, where Σ is the mass surface density. We measured Σ(R) by summing the baryonic mass of the galaxies in an inner circle of radius 200 kpc and five outer annuli with a width of 150 kpc. This gives five radial bins that contain 18, eight, nine, five, and three galaxies from the innermost to the outermost bin. Stellar masses for the satellites are derived either from Ks-band magnitudes (where available) according to the Local Volume (LV) catalog adopting a mass-to-light ratio of 0.6 (McGaugh & Schombert 2014, 2015, the near infrared yields almost constant mass-to-light ratios), or from V-band magnitudes according to Müller et al. (2019) with a mass-to-light ratio of 2.0 (see e.g., Lelli et al. 2017, for typical mass-to-light ratio values). When available, the cold gas mass was added to obtain the total baryonic mass, using Mgas = 1.33MHI where MHI is the measured HI mass and the factor 1.33 takes the contribution of Helium into account. One galaxy (NGC 4945) was removed from this analysis because it is two orders of magnitude more massive than the rest of the dwarf galaxies, leading to a sudden jump in the third radial bin. Fitting the resulting density profile with a power law, we obtained ∂lnΣ/∂lnR = −3.8 ± 1.5, which is consistent with the outer slope of a NFW profile (Navarro et al. 1997). Because the bins were chosen arbitrarily and there are uncertainties in the stellar masses of the satellites, we double checked this fit using an MC approach. We randomly selected the innermost and outermost ellipses to be within ± 100 kpc of the initially chosen radii, and the radial bins having a width between 100 kpc and 200 kpc. We varied the baryonic masses within a factor of 0.5 and 2. We repeatedly fitted the density profile using these randomizations and found that the slope of the density profile varied by ± 1.3, which is consistent with the error coming from the fit (± 1.5). If we turn off the randomization of the mass-to-light ratios, the variation does not change.

We obtained a circular velocity of vcirc = 258 ± 57 km s−1. The uncertainty of the circular velocity was derived through an error propagation of Eq. (4) using the rotational velocity vrot, the velocity dispersion σint, and the fitted slope of the density profile ∂lnΣ/∂lnR, contributing to 17 km s−1, 32 km s−1, and 44 km s−1, respectively.

If we assume that there is some mild tangential anisotropy ( σ R 2 = σ z 2 = 2 σ ϕ 2 $ \sigma_{\rm R}^2 = \sigma_{\rm z}^2 = 2 \sigma_{\phi}^2 $), Equation (5) is replaced by ∂lnρ/∂lnR + 0.5. Then, the circular velocity decreases by ∼15 km s−1, which is smaller than our random errors on vcirc (∼60 km s−1).

3.2. Dynamical and baryonic masses

To estimate the dynamical mass of the group, we used the mean circular velocity and the maximal distance of the satellite population

M tot ( < R max ) = R max v circ 2 G . $$ \begin{aligned} M_{\rm tot}(<R_{\rm max})=\frac{R_{\rm max}{v}_{\rm circ}^2}{G}. \end{aligned} $$(6)

With vcirc = 258 ± 57 km s−1 and Rmax = 801 kpc, we got a dynamical mass of 12.4 ± 5.5 × 1012 M⊙.

In a ΛCDM cosmological context, the properties of cosmic structures are usually given in terms of a density contrast Δ with respect to the critical density of the Universe ρc. One then defines RΔ as the radius at which the mass volume density is equal to Δρc. If we assume that vcirc corresponds to the circular velocity at radius RΔ, the total mass (baryons and dark matter) is given by the following (see, e.g., McGaugh 2012):

M Δ = ( Δ / 2 ) − 1 / 2 ( G H 0 ) − 1 v circ 3 , $$ \begin{aligned} M_{\Delta }=(\Delta /2)^{-1/2}(GH_0)^{-1}{v}_{\rm circ}^3, \end{aligned} $$(7)

where H0 = 75.1 ± 3.8 km s−1 Mpc−1 (Schombert et al. 2020) is the Hubble constant5, and RΔ is given by

R Δ = G M Δ v circ 2 . $$ \begin{aligned} R_{\Delta }=\frac{G M_{\Delta }}{{v}_{\rm circ}^2}. \end{aligned} $$(8)

Adopting Δ = 200, we derived M200 = 5.3 ± 3.5 × 1012 M⊙ within R200 = 344 kpc.

Now we need to estimate the baryonic mass of the Cen A group. This is the baryonic mass locked into all confirmed galaxy members, neglecting the possible inter-galactic medium and the gas mass of Cen A, which is negligible compared to its stellar mass (MHI/LB = 0.01, Struve et al. 2010). Cen A contributes for most of the group mass (1.54 × 1011 M⊙ from Romanowsky & Fall (2012), rescaled to a distance of 3.68 Mpc), while the satellite galaxies add another 0.34 × 1011 M⊙. We estimated the baryonic mass of the Cen A group to be 1.9 × 1011 M⊙. We then derived a baryon fraction fb = Mb/M200 ≃ 0.035. This estimate is significantly lower than the baryon fraction expected from ΛCDM fits to the cosmic microwave background: Ωb/Ωm = 0.157 (Planck Collaboration VI 2020). This is another facet of the so-called missing baryons problem (McGaugh et al. 2010), which now emerges in a whole galaxy group rather than in a single galaxy. The amount of missing baryons in the Cen A group (∼77%) is comparable to that in typical massive galaxies (Katz et al. 2018). This discrepancy is usually explained assuming that the missing baryons reside in a hot, diffuse gas phase that is difficult to detect and quantify. In a ΛCDM context, therefore, we expect that the Cen A group should contain ∼ 8× 1011 M⊙ in hot gas. There is a hot X-ray halo and filamentary structure detected in association with Cen A (Forman et al. 1985). Using the most recent X-ray observations, Gaspari et al. (2019) found that the hot gas mass of Cen A is only ∼3 × 108 M⊙ within 15 kpc (the observed size of the X-ray halo) and increases to ∼3 × 1010 M⊙ when extrapolating out to ∼300 kpc. This latter mass estimate is still ∼27 times smaller than that expected from the cosmic baryon fraction.

Some authors use different density contrasts to define the characteristic quantities of a cosmic structure. If we use Δ = 100, we get M100 = 7.5 ± 5.0 × 1012 M⊙ within a virial radius R100 = 487 kpc. In this case, Cen A would have a baryon fraction of fb ≃ 0.025 and be missing about 84% of the cosmologically available baryons. Clearly, the missing baryon problem in Cen A becomes even worse if we consider the dynamical mass of 1.2 × 1013 M⊙ out to the last measurable radius (∼800 kpc): then the baryon fraction decreases to a mere ∼0.02 and the amount of missing baryons increases to ∼90%.

4. Discussion

4.1. Comparison with previous mass estimates

The dynamical mass of Cen A has been estimated by several authors using different techniques. Studies based on globular clusters (Peng et al. 2004b; Woodley et al. 2010) and/or planetary nebulae (Peng et al. 2004a; Samurović 2016) probe the inner 40−80 kpc, so they trace the gravitational potential of the central galaxy. Here we focus on the dynamical mass of the whole Cen A group (excluding the M83 association).

Table 1 lists mass measurements from the literature in increasing order of physical radius. Our mass estimate within Rmax ≃ 800 kpc is consistent with previous measurements from van den Bergh (2000) and Woodley (2006) within similar radii. Specifically, van den Bergh (2000) used 30 candidate galaxy members (without secure distances at the time, where later observations showed that some of their candidates were not Cen A members, but rather M 83 members, which forms a distinct group, see Tully 2015) assuming spherical symmetry and an isotropic velocity ellipsoid, whereas Woodley (2006) used 13 confirmed members assuming a spherical model with both rotation and dispersion support. We think that our modeling is more reliable because it considers the observed spatial flattening of the satellite systems and deprojects the rotation velocity from the sky plane to the disk plane (see Sect. 2).

Table 1.

Dynamical masses determined for the Cen A group (excluding the M83 subgroup).

Our mass estimate within Rmax ≃ 800 kpc is significantly larger than the value from Karachentsev et al. (2007) at a larger radius (∼1.4 Mpc) from the zero-velocity surface method. On the other hand, our mass estimates within a density contrast of 100 or 200, respectively (R200 = 344 kpc and R100 = 487 kpc), is consistent with the one from Karachentsev et al. (2007) within a similar radius (∼400 kpc) using the virial theorem. We conclude that the zero-velocity method is inferior to estimates using spherical and/or disk models, which display only minor differences.

To address the actual difference between a nonrotating spherical model – which can be considered as the ΛCDM expectation – and a rotating disk model, we repeated the MCMC analysis in Sect. 2 dropping the vmod term in Eq. (3) and fitting only for σint, as it is routinely done in the study of pressure-supported systems (e.g., Mateo et al. 1991; Walker et al. 2009; Taibi et al. 2018; van Dokkum et al. 2019; Emsellem et al. 2019; Collins et al. 2021). We found σint = 131 ± 18 km s−1, which is larger than the previous estimate because the rotational component now enters as a pressure term. To infer the dynamical mass, we adopted the Wolf et al. (2010) estimator that holds when the velocity dispersion profile is approximately flat near the half-mass radius r1/2:

M tot ( < r 1 / 2 ) = 3 r 1 / 2 σ int 2 G . $$ \begin{aligned} M_{\rm tot}({<}r_{\rm 1/2})= \frac{3 r_{\rm 1/2} \sigma _{\rm int}^2}{G}.\end{aligned} $$(9)

For r1/2 = 130 kpc (approximated by the median separation of the satellite system), we derived a dynamical mass of 1.6 ± 0.4 × 1012 M⊙ for such a nonrotating spherical model. If we use Eq. (6) at the same radius, we derive a dynamical mass of 2.0 ± 0.4 × 1012 M⊙ for the rotating disk model. These two values are consistent within the errors, but we consider the rotating disk model better because the satellite system of Cen A is clearly nonspherical.

4.2. Baryonic Tully-Fisher relation and MOND

Having measured the circular velocity and baryonic mass of the Cen A group, we can investigate its position on the baryonic Tully-Fisher relation (BTFR, McGaugh et al. 2000). The BTFR is an empirical relationship between the baryonic mass of a galaxy and the circular velocity along the flat part of the rotation curve, pointing to a tight coupling between baryons and dark matter (e.g., Lelli et al. 2016b, 2019). Figure 3 shows the location of the Cen A group on the BTFR defined by late-type galaxies from the SPARC database (Lelli et al. 2016a) as well as early-type galaxies from Atlas3D (den Heijer et al. 2015). Our measurement of the Cen A group falls right on top of the BTFR. This is remarkable because we are comparing individual galaxies with a whole galaxy group, whose formation and evolution history is presumably governed by different processes on larger scales.

thumbnail Fig. 3.

BTFR of galaxies. The gray dots are late-type galaxies taken from the SPARC database (Lelli et al. 2016b, 2019), the yellow triangles are early-type galaxies (ETGs) from den Heijer et al. (2015), and the red dot indicates our measurement of the Cen A group. The black line is the best fit of the BTFR, and the dashed line is the ΛCDM prediction assuming the cosmic baryon fraction (Planck Collaboration VI 2020).

The location of Cen A on the BTFR agrees with the expectations of Milgromian Dynamics (MOND, Milgrom 1983a,b,c). MOND is an alternative to particle dark matter, in which the Newtonian laws of gravity and/or inertia are modified at accelerations smaller than ∼10−10 m s−2 (Famaey & McGaugh 2012). In a MOND context, the BTFR represents a fundamental law of Nature that should be followed by any isolated gravitational system in equilibrium, independently of its formation and evolution. MOND has been successfully tested in Cen A using globular clusters (Samurović 2016). Figure 3 extends such a test out to much larger radii. In a MOND context, the Cen A group should contain little (if any) missing baryons. This is in line with the study of Milgrom (2019) for a sample of 56 galaxy groups. We note that, in MOND, the internal gravity of the Cen A group would dominate over the external one within ∼500 kpc (Oria et al. 2021), and a drop of 60 km s−1 would be expected at 800 kpc due to the external field effect arising from the cosmic large-scale structure (see e.g., Haghi et al. 2019; Freundlich et al. 2022; Chae et al. 2021), which is within our error bar for the global vcirc value.

5. Summary and conclusions

We studied the dynamics of the Cen A galaxy group using accurate 3D distances and line-of-sight velocities of its member galaxies. Our main results can be summarized as follows:

  1. We used a Bayesian model to study the kinematics of the satellite system considering both rotation and random motions. The ratio between the mean rotation velocity and the mean velocity dispersion is ∼0.7, indicating that the satellite system has significant rotational support.

  2. Assuming an axisymmetric and isotropic (in velocity space) satellite system, we derived a mean circular velocity of 258 km s−1. This translates into a dynamical mass of 1.2 × 1013 M⊙ within 800 kpc (the distance of the outermost satellite from Cen A).

  3. In a ΛCDM context, we derived a virial mass M200 = 5.3 ± 3.5 × 1012 M⊙ within a virial radius R200 = 344 kpc. This gives a baryon fraction Mb/M200 = 0.035 implying that about 77% of the cosmologically available baryons are missing. The missing baryons may be in a hot diffuse medium with a mass of ∼8 × 1011 M⊙, which is ∼4 times larger than the mass locked in stars and gas within galaxies. The expected hot gas mass is more than one order of magnitude larger than that inferred from the most recent X-ray observations. On the other hand, at the galaxy level, M*/M200 ≈ 0.03 for Cen A is much higher than predicted by common abundance matching relations (e.g., Moster et al. 2013; Behroozi et al. 2013), but it is compatible within scatter and error bars with the stellar-to-halo-mass relation from Kravtsov et al. (2018).

  4. Cen A group lies on the baryonic Tully-Fisher relation defined by individual galaxies. This is in agreement with MOND predictions with no need for a significant amount of unaccounted baryons.

With still many dwarf galaxy candidates around Cen A lacking distance and velocity information, our results can be improved with future measurements.

2

Extragalactic Distance Database: http://edd.ifa.hawaii.edu/

3

However, velocities derived from stellar tracers are systematically lower (by 10–20 km s−1) than the HI measurement. This is still within the error, but it may indicate that the gas is moving with respect to the stellar component of Cen A, which could be explained by Cen A’s recent major merger (Wang et al. 2020).

4

These are KKs53 (Tully et al. 2015), CenA-MM-Dw11, CenA-MM-Dw5, CenA-MM-Dw4, CenA-MM-Dw10, CenA-MM-Dw6, CenA-MM-Dw7, CenA-MM-Dw2, CenA-MM-Dw1, CenA-MM-Dw3, CenA-MM-Dw9, CenA-MM-Dw8 (Crnojević et al. 2014, 2019), KK213, KK217, and CenN (Karachentsev et al. 2002).

5

The exact value of the Hubble constant is highly debated, but generally ranges between 67 and 75 km s−1 Mpc−1, with uncertainties on the order of 2–5 km s−1 Mpc−1 (Freedman et al. 2019; Planck Collaboration VI 2020; Kourkchi et al. 2020; Khetan et al. 2021; Riess et al. 2021). Here, we adopt a Hubble constant based on the baryonic Tully-Fisher relation (BTFR).

Acknowledgments

We thank the referee for the constructive report, which helped to clarify and improve the manuscript. O.M. is grateful to the Swiss National Science Foundation for financial support. O.M. also thanks the Arcetri Astrophysical Observatory for its hospitality during his visit. B.F., M.S.P. and O.M. thank the DAAD for PPP grant 57512596 funded by the BMBF, and the Partenariat Hubert Curien (PHC) for PROCOPE project 44677UE. B.F. acknowledges funding from the Agence Nationale de la Recherche (ANR projects ANR-18-CE31-0006 and ANR-19-CE31-0017), and from the European Research Council (ERC) under the European Union’s Horizon 2020 Framework programme (grant agreement number 834148). M.S.P. is funded by a Leibniz-Junior Research Group grant (project number J94/2020) via the Leibniz Competition, and further thanks the Klaus Tschira Stiftung gGmbH and German Scholars Organization e.V. for support via a Klaus Tschira Boost Fund. K.F. acknowledges support through the European Space Agency fellowship programme.

References

  1. Banik, I., & Zhao, H. 2018, MNRAS, 473, 4033 [NASA ADS] [CrossRef] [Google Scholar]
  2. Banks, G. D., Disney, M. J., Knezek, P. M., et al. 1999, ApJ, 524, 612 [NASA ADS] [CrossRef] [Google Scholar]
  3. Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bouchard, A., Jerjen, H., Da Costa, G. S., & Ott, J. 2007, ApJ, 133, 261 [CrossRef] [Google Scholar]
  5. Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [Google Scholar]
  6. Byun, W., Sheen, Y.-K., Park, H. S., et al. 2020, ApJ, 891, 18 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chae, K.-H., Desmond, H., Lelli, F., McGaugh, S. S., & Schombert, J. M. 2021, ApJ, 921, 104 [NASA ADS] [CrossRef] [Google Scholar]
  8. Collins, M. L. M., Read, J. I., Ibata, R. A., et al. 2021, MNRAS, 505, 5686 [NASA ADS] [CrossRef] [Google Scholar]
  9. Côté, S., Freeman, K. C., Carignan, C., & Quinn, P. J. 1997, AJ, 114, 1313 [CrossRef] [Google Scholar]
  10. Côté, P., McLaughlin, D. E., Hanes, D. A., et al. 2001, ApJ, 559, 828 [CrossRef] [Google Scholar]
  11. Crnojević, D., Grebel, E. K., & Cole, A. A. 2011, A&A, 530, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Crnojević, D., Sand, D. J., Bennet, P., et al. 2019, ApJ, 872, 80 [Google Scholar]
  13. Crnojević, D., Sand, D. J., Caldwell, N., et al. 2014, ApJ, 795, L35 [CrossRef] [Google Scholar]
  14. den Heijer, M., Oosterloo, T. A., Serra, P., et al. 2015, A&A, 581, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Doyle, M. T., Drinkwater, M. J., Rohde, D. J., et al. 2005, MNRAS, 361, 34 [NASA ADS] [CrossRef] [Google Scholar]
  16. Emsellem, E., van der Burg, R. F. J., Fensch, J., et al. 2019, A&A, 625, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Fahrion, K., Lyubenova, M., Hilker, M., et al. 2020a, A&A, 637, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fahrion, K., Müller, O., Rejkuba, M., et al. 2020b, A&A, 634, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Rel., 15, 10 [Google Scholar]
  20. Forman, W., Jones, C., & Tucker, W. 1985, ApJ, 293, 102 [NASA ADS] [CrossRef] [Google Scholar]
  21. Freedman, W. L., Madore, B. F., Hatt, D., et al. 2019, ApJ, 882, 34 [Google Scholar]
  22. Freundlich, J., Famaey, B., Oria, P. A., et al. 2022, A&A, 658, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gaspari, M., Eckert, D., Ettori, S., et al. 2019, ApJ, 884, 169 [NASA ADS] [CrossRef] [Google Scholar]
  24. Haghi, H., Kroupa, P., Banik, I., et al. 2019, MNRAS, 487, 2441 [CrossRef] [Google Scholar]
  25. Harris, G. L. H., Rejkuba, M., & Harris, W. E. 2010, PASA, 27, 457 [NASA ADS] [CrossRef] [Google Scholar]
  26. Heesters, N., Habas, R., Marleau, F. R., et al. 2021, A&A, 654, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, NAT, 493, 62 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jerjen, H., Binggeli, B., & Freeman, K. C. 2000a, AJ, 119, 593 [NASA ADS] [CrossRef] [Google Scholar]
  29. Jerjen, H., Freeman, K. C., & Binggeli, B. 2000b, AJ, 119, 166 [NASA ADS] [CrossRef] [Google Scholar]
  30. Karachentsev, I. D. 2005, AJ, 129, 178 [NASA ADS] [CrossRef] [Google Scholar]
  31. Karachentsev, I. D., Sharina, M. E., Dolphin, A. E., et al. 2002, A&A, 385, 21 [CrossRef] [EDP Sciences] [Google Scholar]
  32. Karachentsev, I. D., Tully, R. B., Dolphin, A., et al. 2007, AJ, 133, 504 [NASA ADS] [CrossRef] [Google Scholar]
  33. Karachentsev, I. D., Kashibadze, O. G., Makarov, D. I., & Tully, R. B. 2009, MNRAS, 393, 1265 [NASA ADS] [CrossRef] [Google Scholar]
  34. Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [Google Scholar]
  35. Kashibadze, O. G., & Karachentsev, I. D. 2018, A&A, 609, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Katz, H., Desmond, H., Lelli, F., et al. 2018, MNRAS, 480, 4287 [NASA ADS] [CrossRef] [Google Scholar]
  37. Khetan, N., Izzo, L., Branchesi, M., et al. 2021, A&A, 647, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kirby, E. M., Koribalski, B., Jerjen, H., & López-Sánchez, Á. 2012, MNRAS, 420, 2924 [NASA ADS] [CrossRef] [Google Scholar]
  39. Koribalski, B. S., Staveley-Smith, L., Kilborn, V. A., et al. 2004, AJ, 128, 16 [Google Scholar]
  40. Kourkchi, E., & Tully, R. B. 2017, ApJ, 843, 16 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kourkchi, E., Tully, R. B., Eftekharzadeh, S., et al. 2020, ApJ, 902, 145 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kravtsov, A. V., Vikhlinin, A. A., & Meshcheryakov, A. V. 2018, Astron. Lett., 44, 8 [Google Scholar]
  43. Kroupa, P., Famaey, B., de Boer, K. S., et al. 2010, A&A, 523, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Lelli, F., Fraternali, F., & Verheijen, M. 2014, A&A, 563, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, AJ, 152, 157 [Google Scholar]
  46. Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016b, ApJ, 816, L14 [Google Scholar]
  47. Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
  48. Lelli, F., McGaugh, S. S., Schombert, J. M., Desmond, H., & Katz, H. 2019, MNRAS, 484, 3267 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lewis, G. F., Brewer, B. J., & Wan, Z. 2020, MNRAS, 491, L1 [NASA ADS] [CrossRef] [Google Scholar]
  50. Libeskind, N. I., Hoffman, Y., Tully, R. B., et al. 2015, MNRAS, 452, 1052 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lynden-Bell, D. 1981, The Observatory, 101, 111 [NASA ADS] [Google Scholar]
  52. Martínez-Delgado, D., Makarov, D., Javanmardi, B., et al. 2021, A&A, 652, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Mateo, M., Olszewski, E., Welch, D. L., Fischer, P., & Kunkel, W. 1991, AJ, 102, 914 [NASA ADS] [CrossRef] [Google Scholar]
  54. McGaugh, S. S. 2012, AJ, 143, 40 [Google Scholar]
  55. McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [Google Scholar]
  56. McGaugh, S. S., & Schombert, J. M. 2015, ApJ, 802, 18 [NASA ADS] [CrossRef] [Google Scholar]
  57. McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [Google Scholar]
  58. McGaugh, S. S., Schombert, J. M., de Blok, W. J. G., & Zagursky, M. J. 2010, ApJ, 708, L14 [NASA ADS] [CrossRef] [Google Scholar]
  59. Milgrom, M. 1983a, ApJ, 270, 365 [Google Scholar]
  60. Milgrom, M. 1983b, ApJ, 270, 371 [Google Scholar]
  61. Milgrom, M. 1983c, ApJ, 270, 384 [Google Scholar]
  62. Milgrom, M. 2019, Phys. Rev. D, 99, 044041 [NASA ADS] [CrossRef] [Google Scholar]
  63. Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [Google Scholar]
  64. Müller, O., Jerjen, H., & Binggeli, B. 2015, A&A, 583, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Müller, O., Jerjen, H., Pawlowski, M. S., & Binggeli, B. 2016, A&A, 595, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Müller, O., Scalera, R., Binggeli, B., & Jerjen, H. 2017, A&A, 602, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Müller, O., Pawlowski, M. S., Jerjen, H., & Lelli, F. 2018, Science, 359, 534 [CrossRef] [Google Scholar]
  68. Müller, O., Rejkuba, M., Pawlowski, M. S., et al. 2019, A&A, 629, A18 [Google Scholar]
  69. Müller, O., Pawlowski, M. S., Lelli, F., et al. 2021a, A&A, 645, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Müller, O., Fahrion, K., Rejkuba, M., et al. 2021b, A&A, 645, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
  72. Oppenheimer, B. D., Babul, A., Bahé, Y., Butsky, I. S., & McCarthy, I. G. 2021, Universe, 7, 209 [NASA ADS] [CrossRef] [Google Scholar]
  73. Oria, P. A., Famaey, B., Thomas, G. F., et al. 2021, ApJ, 923, 68 [NASA ADS] [CrossRef] [Google Scholar]
  74. Pawlowski, M. S. 2018, Mod. Phys. Lett. A, 33, 1830004 [NASA ADS] [CrossRef] [Google Scholar]
  75. Pawlowski, M. S., & Kroupa, P. 2020, MNRAS, 491, 3042 [NASA ADS] [CrossRef] [Google Scholar]
  76. Pawlowski, M. S., & Tony Sohn, S. 2021, ApJ, 923, 42 [NASA ADS] [CrossRef] [Google Scholar]
  77. Pawlowski, M. S., Pflamm-Altenburg, J., & Kroupa, P. 2012, MNRAS, 423, 1109 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pawlowski, M. S., Kroupa, P., & Jerjen, H. 2013, MNRAS, 435, 1928 [NASA ADS] [CrossRef] [Google Scholar]
  79. Peng, E. W., Ford, H. C., & Freeman, K. C. 2004a, ApJ, 602, 685 [CrossRef] [Google Scholar]
  80. Peng, E. W., Ford, H. C., & Freeman, K. C. 2004b, ApJ, 602, 705 [NASA ADS] [CrossRef] [Google Scholar]
  81. Peterson, R. C., & Caldwell, N. 1993, AJ, 105, 1411 [NASA ADS] [CrossRef] [Google Scholar]
  82. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Puzia, T. H., & Sharina, M. E. 2008, ApJ, 674, 909 [NASA ADS] [CrossRef] [Google Scholar]
  84. Rejkuba, M. 2004, A&A, 413, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
  86. Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [Google Scholar]
  87. Samurović, S. 2016, Ap&SS, 361, 199 [CrossRef] [Google Scholar]
  88. Sandage, A. 1986, ApJ, 307, 1 [NASA ADS] [CrossRef] [Google Scholar]
  89. Santos-Santos, I. M., Domínguez-Tenreiro, R., & Pawlowski, M. S. 2020, MNRAS, 499, 3755 [NASA ADS] [CrossRef] [Google Scholar]
  90. Saviane, I., & Jerjen, H. 2007, AJ, 133, 1756 [NASA ADS] [CrossRef] [Google Scholar]
  91. Schombert, J., McGaugh, S., & Lelli, F. 2020, AJ, 160, 71 [NASA ADS] [CrossRef] [Google Scholar]
  92. Struve, C., Oosterloo, T. A., Morganti, R., & Saripalli, L. 2010, A&A, 515, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Taibi, S., Battaglia, G., Kacharov, N., et al. 2018, A&A, 618, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Taylor, M. A., Eigenthaler, P., Puzia, T. H., et al. 2018, ApJ, 867, L15 [NASA ADS] [CrossRef] [Google Scholar]
  95. Tully, R. B. 2015, AJ, 149, 54 [NASA ADS] [CrossRef] [Google Scholar]
  96. Tully, R. B., Shaya, E. J., Karachentsev, I. D., et al. 2008, ApJ, 676, 184 [Google Scholar]
  97. Tully, R. B., Rizzi, L., Shaya, E. J., et al. 2009, AJ, 138, 323 [NASA ADS] [CrossRef] [Google Scholar]
  98. Tully, R. B., Libeskind, N. I., Karachentsev, I. D., et al. 2015, ApJ, 802, L25 [Google Scholar]
  99. van den Bergh, S. 2000, AJ, 119, 609 [NASA ADS] [CrossRef] [Google Scholar]
  100. van Dokkum, P., Danieli, S., Abraham, R., Conroy, C., & Romanowsky, A. J. 2019, ApJ, 874, L5 [Google Scholar]
  101. Veljanoski, J., & Helmi, A. 2016, A&A, 592, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009, ApJ, 704, 1274 [Google Scholar]
  103. Wang, J., Hammer, F., Rejkuba, M., Crnojević, D., & Yang, Y. 2020, MNRAS, 498, 2766 [NASA ADS] [CrossRef] [Google Scholar]
  104. Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
  105. Woodley, K. A. 2006, AJ, 132, 2424 [NASA ADS] [CrossRef] [Google Scholar]
  106. Woodley, K. A., Gómez, M., Harris, W. E., Geisler, D., & Harris, G. L. H. 2010, AJ, 139, 1871 [NASA ADS] [CrossRef] [Google Scholar]
  107. Zwicky, F. 1933, Helv. Phys. Acta, 6, 110 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Dynamical masses determined for the Cen A group (excluding the M83 subgroup).

In the text

All Figures

thumbnail Fig. 1.

Posterior distribution of the five fitting parameters from the MCMC analysis of the Cen A satellite system. In the histograms, the three dashed lines indicate the 16, 50, and 84 percentiles, which correspond to the upper and lower uncertainty boundaries, and the best-fit parameter estimation (i.e., the median). See Sect. 2 for details.
In the text
thumbnail Fig. 2.

Position-velocity diagram along the projected major axis of the satellite system. Red dots with 1σ error bars show satellites of Cen A with measured line-of-sight velocities. The contours represent the best-fit rotating disk model with vrot = 90 km s−1 and σint = 124 km s−1. The inner and outer contours correspond to 1σ and 2σ probabilities of finding a galaxy at that location of the position-velocity diagram.
In the text
thumbnail Fig. 3.

BTFR of galaxies. The gray dots are late-type galaxies taken from the SPARC database (Lelli et al. 2016b, 2019), the yellow triangles are early-type galaxies (ETGs) from den Heijer et al. (2015), and the red dot indicates our measurement of the Cen A group. The black line is the best fit of the BTFR, and the dashed line is the ΛCDM prediction assuming the cosmic baryon fraction (Planck Collaboration VI 2020).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

OSZAR »