| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A175 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202243580 | |
| Published online | 29 August 2022 | |
Low-mass young stars in the Milky Way unveiled by DBSCAN and Gaia EDR3: Mapping the star forming regions within 1.5 kpc★
1
INAF – Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
90134
Palermo, Italy
e-mail: [email protected]
2
CEICO, Institute of Physics of the Czech Academy of Sciences,
Na Slovance 2,
182 21
Praha 8, Czechia
3
Astrophysics Group, Keele University,
Keele,
Staffordshire
ST5 5BG, UK
4
INAF – Osservatorio Astronomico di Capodimonte,
via Moiariello 16,
80131
Napoli, Italy
Received:
18
March
2022
Accepted:
26
May
2022
Context. With an unprecedented astrometric and photometric data precision, Gaia EDR3 provides, for the first time, the opportunity to systematically detect and map, in the optical bands, the low-mass populations of the star forming regions (SFRs) in the Milky Way.
Aims. We aim to provide a catalogue of the Gαiα EDR3 data (photometry, proper motions and parallaxes) of the young stellar objects (YSOs) identified in the Galactic plane |b| < 30°) within about 1.5 kpc. The catalogue of the SFRs to which they belong is also provided to study the properties of the very young clusters and put them in the context of the Galaxy structure.
Methods. We applied the machine learning unsupervised clustering algorithm density-based spatial clustering of applications with noise (DBSCAN) to a sample of Gaia EDR3 data photometrically selected on the region where very young stars (t ≲ 10 Myr) are expected to be found, with the aim of identifying co-moving and spatially consistent stellar clusters. A sub-sample of 52 clusters, selected among the 7 323 found with DBSCAN, has been used as template data set to identify very young clusters from the pattern of the observed colour-absolute magnitude diagrams through a pattern-match process.
Results. We find 124440 candidate YSOs clustered in 354 SFRs and stellar clusters younger than 10 Myr and within ≲ 1.5 kpc. In addition, 65 863 low-mass members of 322 stellar clusters located within ~500pc and with ages 10Myr ≲ t ≲ 100 Myr were also found.
Conclusions. The selected YSOs are spatially correlated with the well-known SFRs. Most of them are associated with well-concentrated regions or complex structures of the Galaxy, and a substantial number of them have been recognised for the first time. The massive SFRs, such as, for example, Orion, Sco-Cen, and Vela, located within 600–700 pc trace a very complex three-dimensional pattern, while the farthest ones seem to follow a more regular pattern along the Galactic plane.
Key words: methods: data analysis / open clusters and associations: general / catalogs / surveys / stars: formation / stars: pre-main sequence
Tables 3 and 4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/664/A175
© L. Prisinzano et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
It is now well known that stars originate from the collapse of cold molecular clouds and mainly form in over-dense structures and clusters usually designated as star forming regions (SFRs). During the very early phases, young stellar objects (YSOs) can be identified in the near-, mid-, and far-infrared (IR) and radio wavelengths because of the presence of the optically thick infalling envelope or circumstellar disc around the central star. In the subsequent pre-main-sequence phase, they also become visible in the optical bands. However, when the final dispersal of the disc material occurs and non-accreting transition discs form, YSOs can no longer be identified in IR or radio surveys (Ercolano et al. 2021) and a complete census is only possible in the optical bands.
While a clean identification of YSOs is very hard using only optical photometry, an efficient way to systematically single out SFRs is by the identification of kinematical stellar groups with a common space motion. With an unprecedented astrometric precision and sky coverage, Gaia data offer the possibility to recognise the SFRs as common proper motion groups, at least within the Gaia observational limits.
Data from the Gaia mission are revolutionising our ability to map the youngest stellar populations of the Milky Way in the optical bands, which is one of the core science goals for an overall understanding of the Galactic components. The youngest stellar component is crucial to better characterising the Galactic thin disc and its spiral arms and to understanding its origin.
The characterisation of individual SFRs and their dynamics are also fundamental to understanding the local formation, evolution, and dispersion of star clusters, as well as the star formation history and the initial mass function (IMF). Finally, statistical studies of YSOs during the early years of their formation, when the proto-planetary discs are evolving and planets form, are crucial to shedding light on planet formation theory.
With more than 1.3 billion stars with precise proper motions and astrometric (positions and parallaxes) and photometric measurements, Gaia DR2 data allowed several studies aimed at identifying clustered populations of the Milky Way. Some of these studies have been dedicated to SFRs, associations, and moving groups. Zari et al. (2018) presented an analysis of the clustered and diffuse young populations within 500 pc, using a combination of photometric and astrometric criteria. Analogously, Kerr et al. (2021) studied the solar neighbourhood by applying the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) algorithm (McInnes et al. 2017). They found 27 young groups, associations, and significant sub-structures, associated with known clusters and SFRs, and released a catalogue including ~3 × 104 Gaia DR2 YSOs within 333 pc.
Cantat-Gaudin et al. (2018) started from a list of known clusters to assign them unsupervised membership and parameters. Other studies have been dedicated to systematically finding open clusters in the Galaxy. Castro-Ginard et al. (2018) used the density-based spatial clustering of applications with noise (DBSCAN) algorithm (Ester et al. 1996) to select a list of candidate open clusters (OC), which they then refined to identify real OCs with a well-defined main sequence (MS). Other papers have recently been published detailing the discoveries of new open clusters and the deduction of their parameters (e.g. Cantat-Gaudin & Anders 2020; Cantat-Gaudin et al. 2020; Castro-Ginard et al. 2020; Liu & Pang 2019).
A recent attempt to find Galactic plane (GP) clustered populations, including SFRs, was made by Kounkel & Covey (2019) and Kounkel et al. (2020), again using Gaia DR2 data and the HDBSCAN unsupervised algorithm in 5D space (l, b, π,  , µδ). In these works, the first limited to 1 kpc and the second to 3 kpc, they found clustered populations, associations, moving groups, and string-like structures, parallel to the GP, spanning hundreds of parsec in length. Clusters aged between 10 Myr and 1 Gyr have been found with an onion-like approach using the entire catalogue with different cut-offs in parallax and progressively merging the different catalogues.
, µδ). In these works, the first limited to 1 kpc and the second to 3 kpc, they found clustered populations, associations, moving groups, and string-like structures, parallel to the GP, spanning hundreds of parsec in length. Clusters aged between 10 Myr and 1 Gyr have been found with an onion-like approach using the entire catalogue with different cut-offs in parallax and progressively merging the different catalogues.
A different approach was adopted by Bica et al. (2019), who used infrared (IR) data from 2MASS, WISE, VVV, Spitzer, and Herschel surveys to compile a catalogue of 10 978 Galactic star clusters, and associations, including 4234 embedded clusters.
With the advent of Gaia Early Data Release 3 (EDR3), based on 34 months of observations1, available photometric and astrometric measurements improved significantly. In particular, photometric improvements have been made in the calibration models, in the different photometric systems, and in the treatment of the BP and RP local background flux (Riello et al. 2021).
In this work, we used Gaia EDR3 data to systematically identify the low-mass component of SFRs in the Galaxy, with ages approximately <10 Myr and within a distance limit of ~ 1.5 kpc imposed by our data selection. We focused our analysis on very young clusters by exploiting the significant progress achieved with Gaia EDR3 data. A full exploitation of the Gaia data and the results presented here would require further data, such as spectroscopic determination of individual stellar parameters, such as effective temperatures, gravities, and stellar luminosities, as well as rotational and radial velocities, which are crucial to deriving masses, ages, and 3D space velocities. Even though the results presented here cannot be used at this stage to determine the IMF, star formation history, and 3D kinematics of the SFRs, they can be used to trace the very young Galactic stellar component within 1.5–2 kpc through a systematic method that homogeneously identifies the bulk population of the SFRs. Such results can be used both for statistical and individual detailed analyses. The paper is organised as follows. In 2, we describe the requirements adopted to select the Gaia EDR3 data, and in 3 the photometric selection applied to obtain the starting sample of the YSO candidates. In 4, we describe the method adopted to identify SFRs and stellar clusters, the criteria adopted to validate them, and the age classification. Our results and the discussion are presented in Sects. 5 and 6, respectively; finally, our summary and conclusions are presented in Sect 7. In Appendix A we show the effects of the reddening in the Gaia colour-absolute magnitude diagrams, in Appendix B we estimate the effect of multiplicity in the selection of the YSOs, while in Appendix C we describe the comparison of specific regions with the literature.
2 Gaia data
In this analysis, we used the Gaia EDR3 data (Gaia Collaboration 2016, 2021), which provide precise astrometry and kinematics (l, b, π,  , µδ) as well as excellent photometry in three broad bands (G, GBP, GRP). Since our analysis is focussed on the Galactic midplane, where most of the YSOs are expected to be found, we selected sources within |b| < 30°. We limited our selection to 7.5 < G ≤ 20.5. The limit G = 7.5 was chosen in order to discard objects with magnitudes derived from saturated charge-coupled device (CCD) images, while G = 20.5 is the limit to include most of the objects with magnitude G uncertainties lower than 0.2 mag. This range includes the young, low-mass populations (0.1 ≲ M/M⊙ ≲ 1.5) of the known SFRs within the distance set by the limiting magnitude. In addition, we only considered positive parallax values. This choice does not introduce any bias since we do not expect to investigate stars with very small parallaxes that could have negative values (Luri et al. 2018). Finally, we imposed a relative parallax error lower than 20% in order to discard stars with a poorly constrained distance, and, to take into account the Gaia EDR3 systematics, we also considered the renormalised unit weight error (RUWE; Lindegren et al. 2021b), which is expected to be <1.4 for sources where the single-star model provides a good fit to the astrometric observations.
, µδ) as well as excellent photometry in three broad bands (G, GBP, GRP). Since our analysis is focussed on the Galactic midplane, where most of the YSOs are expected to be found, we selected sources within |b| < 30°. We limited our selection to 7.5 < G ≤ 20.5. The limit G = 7.5 was chosen in order to discard objects with magnitudes derived from saturated charge-coupled device (CCD) images, while G = 20.5 is the limit to include most of the objects with magnitude G uncertainties lower than 0.2 mag. This range includes the young, low-mass populations (0.1 ≲ M/M⊙ ≲ 1.5) of the known SFRs within the distance set by the limiting magnitude. In addition, we only considered positive parallax values. This choice does not introduce any bias since we do not expect to investigate stars with very small parallaxes that could have negative values (Luri et al. 2018). Finally, we imposed a relative parallax error lower than 20% in order to discard stars with a poorly constrained distance, and, to take into account the Gaia EDR3 systematics, we also considered the renormalised unit weight error (RUWE; Lindegren et al. 2021b), which is expected to be <1.4 for sources where the single-star model provides a good fit to the astrometric observations.
To summarise, data of our interest were selected from the Astronomical Data Query Language (ADQL) interface of the ESA Gaia Archive2 using the following restrictions:
 (1)
(1)
We also included a photometric condition in the query aimed to include the pre-main-sequence (PMS) region of the MG versus G − GRP colour-absolute magnitude diagram (CAMD) where all very young stars (t ≲ 10 Myr) are expected to be found. We split our selection in two samples, namely bright and faint, according to the following criteria:
 (2)
(2)
 (3)
(3)
These limits are drawn as solid blue and green lines in Fig. 1. We note that in this work, for the reddening uncorrected absolute magnitudes, we adopted the definition MG = G + 5log(π) − 10, based on the inverted Gaia EDR3 parallaxes, since, as shown in Piecka & Paunzen (2021), within <2kpc, the inverse-parallax method gives results comparable to distances derived by the Bayesian approach (Bailer-Jones et al. 2021).
The minimum value MG = 5 was set to avoid the upper region of the colour-absolute magnitude diagram, where the overlap of the upper MS or PMS stars of the SFRs with giants, MS, or turn-off stars is expected to be very high, especially if the reddening is not corrected. This implies a cut of the massive population of the SFRs, but it does not represent an issue for our investigation since we are mainly interested in the rich low-mass component of these populations. In order to further reduce the fraction of contaminants, also we used the condition G − GRP > 0.58, which is the minimum expected unreddened colour for low-mass (M ≲ 1.2 M⊙) PMS (age ≤ 10 Myr) stars.
Our photometric selection and the subsequent analysis are based on the G − GRP colours. This choice allows us to avoid the use of the GBP magnitudes that for G ≳20 are strongly affected by the application of the minimum flux threshold, which overestimates the mean BP flux. This issue also affects the RP flux, but with a considerably lower effect in GRP than in GBP (Riello et al. 2021). Once the data had been retrieved by the ESA Gaia Archive, parallax values were corrected by the zero point bias reported in Lindegren et al. (2021a) using the Python code available to the community3, which is a function of source magnitude, colour, and celestial position.
In addition, we performed further data filtering by only considering objects with errors smaller than 0.14 mag in G − GRP. Standard errors in the magnitudes were computed using the propagations of the flux errors with the following formulas:
 (4)
(4)
 (5)
(5)
 (6)
(6)
where FG, FGBP and FGRP are the mean fluxes in the G, BP, and RP bands, respectively, and σ(G0) = 0.0027553202,  , and
, and  are the Gaia EDR3 zero-point uncertainties4.
are the Gaia EDR3 zero-point uncertainties4.
 |
Fig. 1 CAMD of YSOs of some representative young clusters with membership probabilities >0.90 assigned by combining spectroscopic and Gaia EDR3 criteria (Jackson et al. 2022). Blue x symbols trace the empirical sequence by Pecaut & Mamajek (2013). Members of the clusters Gamma Velorum (18 Myr old) and NGC2451b (50 Myr old) are also shown. Black solid lines are the theoretical solar metallicity Pisa isochrones while the red solid line is the complete photometric limit adopted in this work including the low mass extrapolation. Dashed, dashed-dotted and dotted lines are the 10 Myr isochrones at different metallicities. Blue and green solid lines represent the limits described by the equations 2 and 3. |
3 Photometric selection of the input sample
In this section, we describe and discuss how we performed the final photometric selection of the sample used as input for the subsequent clustering analysis, which is based on the astrometric and kinematic Gaia EDR3 parameters, as described in 4. By considering the typical complexity of the environment of young stars and the dependence of the reddening law from the stellar effective temperature due to the large spectral range covered by the Gaia bands (Anders et al. 2019), we did not attempt to correct colours and magnitudes for reddening and absorption, but we used their observed values. This is certainly one of the main sources of contamination by older stars to be overcome, as we discuss later in the paper.
Our goal is to start from a complete sample, including all potential YSOs with ages <10 Myr, at least in the photometric range set described in 2. In particular, we selected the objects with MG falling on the red side of the solar-metallicity 10 Myr isochrone computed using the PISA models (Dell'Omodarme et al. 2012; Randich et al. 2018; Tognelli et al. 2018, 2020) in the MG versus G − GRP diagram shown in Fig. 1. To check if the selected photometric limit is compliant with our requirements, we compared it with the reddening uncorrected CAMD of some SFRs and young clusters for which membership was recently derived by Jackson et al. (2022) based on the 3D kinematics of the spectroscopic targets. We find that the adopted 10 Myr isocrone delimits the PMS region of clusters, such as NGC 2264, Lambda Ori, Lambda Ori B35, and Rho Ophiuchi, which are in our main age range (t < 10 Myr) of interest. However, members of ~20 Myr old clusters, such as Gamma Velorum, also fall completely in the selected photometric region, while members of ~50-Myr-old clusters, such as NGC 2451b, fall partially in the selected photometric region at MG ≳ 9. Going to clusters with ages of t > 50 Myr the overlapping region occurs at fainter magnitudes.
Since the adopted isochrone is limited to 0.1 M⊙, corresponding to MG = 10.7, the photometric limit at fainter magnitudes was extrapolated using a linear extrapolation. To check the position of such extrapolation, we compared it with the empirical sequence by Pecaut & Mamajek (2013), for which mean stellar colours and effective temperatures are given down to M and L spectral types and that can be used as an upper limit to the region we are interested in. Our photometric limit approaches such a sequence and crosses it at MG ~ 13. This ensures we set an inclusive photometric selection close to the MS at the lowest mass tail. In fact, even though this implies the inclusion of stars older than 10 Myr, it avoids a bias against the selection of very young stars.
We note that for the photometric selection, the minimum and maximum MG associated with each observed star have been computed by considering the 1 σ parallax uncertainties, which are dominant with respect to the magnitude uncertainties. The photometric selection with respect to the reference isochrone was performed by considering the compatibility of MG magnitudes with respect to their minimum and maximum values; that is, they were selected if either their minimum or maximum value lay inside the selection region. At the end of this selection, we were left with a catalogue of 18 057 300 Gaia EDR3 entries.
Performing a photometric selection as inclusive as possible, as we have done, implies the introduction of a significant contamination by old field or open cluster stars, mainly due to the uncorrected reddening, binarity, or overlapping photometric region in the low-mass range, where the sensitivity of the G − GRP colours in distinguishing PMS or MS stars becomes very low. However, the contamination by field stars does not represent a significant issue for our clustering analysis, since they are not expected to share similar astrometric and kinematic properties. In addition, since we aim to investigate the low-mass component of the SFRs, which is also the most dominant (≳80%; Lada 2006), the statistical contrast with respect to field contaminants is expected to be favourable to detecting them.
A more complex effect of our inclusive photometric selection is that clusters older than 10 Myr can also partially fall in the selected region and be recognised as candidate clusters in the subsequent analysis. As shown in Fig. 1, at faint absolute magnitudes (MG > 9), the model-computed isochrones are not very sensitive to stellar ages and tend to overlap, especially in the MG versus G − GRP diagram. In addition, spectral synthesis of M dwarf stars suffers from the accuracy of the adopted atmosphere models and/or from incomplete molecular data. The model-predicted colours of very-low-mass stars are therefore uncertain. A further complication is the observed discrepancy between radii and colours of low-mass stars, likely due to the distorting effects of magnetic activity and star spots on the structure of active stars (Somers et al. 2020; Franciosini et al. 2021). All these effects cause a spread of the low-mass MS and can bring magnitudes and colours of ~100-Myr-old stars to the region selected by us as compatible with stars with t < 10 Myr. For all these reasons, as discussed, for example, in Jeffries et al. (2017), the ages judged from ‘standard’ isochrones are almost certainly underestimated due to a systematic bias.
At faint magnitudes, the fraction of old cluster members falling in the adopted photometric region decreases with cluster ages. Hence, clusters of about 20–30 Myr will be almost completely included in our selected sample, while at the age of 100–500 Myr only the low-mass tail will be included. However, because of the adopted photometric limit, the low-mass tails will be included only for relatively close clusters (d < 500 pc).
As already mentioned before, a partial contamination by old cluster members in our photometric sample can occur also for bright stars (MG < 9–10) if their reddening or a binary status gives them observed magnitudes and colours compatible with the selected photometric region. As shown in Appendix A, the effects of using colours and magnitudes uncorrected for reddening are expected to be more severe for reddened stars with spectral types earlier than G, in comparison with later spectral types, in the sense that the selected sample is expected to be contaminated mainly by these objects, which fall in the brightest part of the photometric region adopted in this work. The implications of this contingency are discussed in the following sections.
Finally, we also considered the possible effects due to the metallicity on the selection by considering 10 Myr isochrones for a metallicity lower or higher than solar. The comparison shows that while YSOs with over-solar (Z = 0.020, [Fe/H] = 0.2) or sub-solar (Z = 0.005, [Fe/H] = −0.45) metallicities would fall in the selected photometric region, very-metal-poor YSOs (Z = 0.001, [Fe/H] = −1.10) would remain outside. However, as recently found by Spina et al. (2017) at galactocentric radii from ~6.5 kpc to 8.70 kpc, young open clusters and SFRs have close-to-solar or slightly sub-solar metallicities, and therefore we conclude that no SFRs are expected to be missed for metallicity effects with our photometric assumptions.
Based on the adopted photometric selection, our data set encompasses all YSOs of ages t ≲ 10 Myr and observed MG > 5, including the most reddened (AV < 3–4) that can be detected with Gaia. Even YSOs with accretion (e.g. Gullbring et al. 1998) or that are seen in scattered light (Bonito et al. 2013) or flares in M-type stars (e.g. Mitra-Kraev et al. 2005) are expected to be included in our sample. In fact, these phenomena affect the GBP − G or the GBP − GRP colours, causing the stellar colours to become bluer than their photospheric colours, while, on the contrary, their effect on the G − GRP colours goes in the same direction as the reddening, causing these latter colours to become redder.
We stress, however, that the constraint MG < 5, adopted to strongly reduce the contamination due to reddened turn-off or MS stars, makes the selected photometric sample incomplete for the massive stellar component of the SFRs. A further expected missing stellar component is that of binary systems of the clusters, due to the restriction of the Gaia data to RUWE < 1.4 (see Appendix B). In addition, since available data do not allow us to obtain reliable corrections for the reddening affecting colours and magnitudes of the selected YSOs, accurate stellar parameters such as individual stellar ages and masses will not be derived in the subsequent analysis. However, even though the results we aim to achieve are not suitable for investigations based on complete young populations or accurate stellar parameters, they are expected to trace the dominant component of the SFRs, that is, their low-mass population, and will be crucial to an overall systematic view of the Galactic SFRs located within 1–2 kpc of the Sun, as well as for detailed individual or statistical investigations of these YSOs.
4 Method
4.1 Clustering with DBSCAN
This section describes the methodology used to search for candidate clusters with an unsupervised algorithm, such as over-densities in the 5D Gaia EDR3 astrometric and kinematics parameters (l, b, π,  , µδ). Starting from the data set selected as described in the 3, we performed a clustering analysis using the DBSCAN code (Ester et al. 1996), within the scikit-learn machine-learning package in Python. First of all, we prepared a grid of 5o × 5° boxes, covering the entire range of the Galactic longitudes l and for |b| < 30°. In this step, we took into account the discontinuity at l = 0°. To homogenise the variables with different dimensions to comparable values, the five parameters (l, b, π,
, µδ). Starting from the data set selected as described in the 3, we performed a clustering analysis using the DBSCAN code (Ester et al. 1996), within the scikit-learn machine-learning package in Python. First of all, we prepared a grid of 5o × 5° boxes, covering the entire range of the Galactic longitudes l and for |b| < 30°. In this step, we took into account the discontinuity at l = 0°. To homogenise the variables with different dimensions to comparable values, the five parameters (l, b, π,  , µδ) within each box were first re-scaled using the RobustScaler Python code based on a statistics robust to outliers, according to the interquartile range.
, µδ) within each box were first re-scaled using the RobustScaler Python code based on a statistics robust to outliers, according to the interquartile range.
The DBSCAN algorithm requires only two input parameters (e, minPts). It identifies candidate clusters as overdensities in a multi-dimensional space (5D in our case) in which the number of sources exceeds the required minimum number of points minPts, within a neighbourhood of a particular linking length, e, for all five parameters, using a statistical distance that is assumed to be Euclidean. DBSCAN does not require us to know an a priori number of clusters, and it is able to detect arbitrarily shaped clusters. This is crucial for our analysis aimed at finding SFRs that can be characterised by circular or elongated or asymmetric shapes, reminiscent of the native molecular clouds. In order to determine the best input parameters (є, minPts) to give as input to DBSCAN, we experimented with several values in the direction of well-known SFRs, and we noted that in the same direction more than a combination of the two parameters is needed to reveal different real clusters located at different distances. This is due to the fact that close candidate clusters, such as associations and co-moving groups, can appear spatially (in l and b) sparse, while they are definitively clustered in distance and proper motions; yet, in the same direction it is possible to identify distant but spatially concentrated candidate clusters. In the two cases, the choice of two different є values rather than a single є is required to detect these kinds of clusters.
Based on this preliminary empirical analysis, we decided to run the DBSCAN codes in the entire GP, by adopting a total of 900 combinations of (є, minPts) values with є ranging from 0.1 to 9 in steps of 0.1 and minPts ranging from 5 to 50 in steps of 5. In addition, to account for candidate clusters falling in the borders of the defined boxes, we defined another four sets of grids by shifting the original boxes by δl = δb = [1°, 2°, 3°, 4°] with respect to the original boxes. In the following, we refer to the five sets of grids as spatial configurations. At the end, we run DBSCAN within a total of 360/5 × 60/5 × 5 = 4320 different boxes with 900 combinations of parameter sets (є, minPts).
4.2 Candidate cluster validation
One of the most challenging phases of this analysis has been the validation of the recognised candidate clusters. In fact, DBSCAN is an unsupervised density-based algorithm, and, as a consequence, it picks up not only overdensities that correspond to real OCs, but also overdensities in purely statistical terms. For this reason, our a posteriori validation approach is based on the exploitation of two astrophysical constraints, based on the typical properties of the SFRs, by avoiding the introduction of strong biases.
Star forming regions are not characterised by well-defined age sequences, and they are typically observed in the Hertzsprung-Russell (HR) diagrams as ensembles showing an apparent luminosity spread, often associated with an age spread (e.g. Palla & Stahler 1999; Palla et al. 2005). On the other hand, such spreads have also been ascribed to complex phenomena affecting their photometry, such as variability, accretion and outflows, extinction, binarity, and our inability to quantify their contribution (Soderblom et al. 2014). Neverthless, SFRs are usually observed with a typical mass distribution that can be shaped by a standard (or closely resembling standard) IMF, characterised by an increasing fraction of members going towards decreasing masses, at least until masses of ~0.3 M⊙ (e.g. Salpeter 1955; Scalo 1998; Chabrier 2003).
Since we exploited the excellent Gaia EDR3 results down to G = 20.5, within reasonable reddening values (AV ≲ 1), with our data set we expect to detect YSOs with spectral types down to M-type and at distances ≲1.5 kpc. This is the case, for example, of the cluster NGC 6530, located at around 1.3 kpc, for which the low-mass population down to 0.4 M⊙ has been detected at V ~ 20 (Prisinzano et al. 2005), roughly corresponding to our G magnitude limit.
Based on these considerations, a physically recognisable candidate cluster should include its tail of low-mass members. Hence, we imposed a minimum threshold of ten objects with MG > 7.7, which means requiring candidate clusters to have at least ten stars with M ≲ 0.5 M⊙, assuming the isochrone of 10 Myr from the Pisa models.
A further parameter that we considered as an indicator of reliability for the candidate cluster validation is the dispersion of the distances of each cluster. The observed total distance dispersion is a combination of the intrinsic dispersion plus the contribution due to the measurement errors. While the intrinsic dispersion does not depend on the distance, the contribution due to the measurement errors becomes dominant at large distances since Gaia EDR3 parallaxes become much more uncertain. Thus, among the parameters used to find overdensities by DBSCAN, the observed standard deviation of the distances is the most critical parameter to be constrained for the identification of real clusters. To this aim, for the cluster validation, we constrained the maximum allowed observed dispersion. For distances <1 kpc, the constraint is set on the ratio between the standard deviation of the distances of the putative members and the derived mean distance for the given candidate cluster. For a valid candidate cluster, the above ratio has to be <0.2. For more distant candidate clusters, we adopted the more stringent constraint that the standard deviation should be smaller than 200 pc. This limit was chosen considering that, for NGC 2244, located at ~1.6 kpc and one of the most distant clusters that we detect, the distance dispersion is about 175 pc, and therefore we do not expect to find real physical clusters with a distance dispersion larger than this threshold. These choices may limit our ability to detect clusters at distance ≳1.5 kpc, for which we could, in principle, detect, at the magnitude limit of our data set, the massive component of the clusters down to ~ 1 M⊙ regime. However, since the accuracy of Gaia EDR3 parallaxes and kinematic data beyond this limit becomes very low, we prefer to maintain our constraints at the cost of limiting our analysis to smaller distances.
The adopted constraints on the distance dispersion of cluster members have shown to be very effective in rejecting a large number of (unexpected) candidate massive clusters recognised by DBSCAN, typically with more than 1000 members located at distances >1 kpc, which do not include M-type stars but only earlier stars and are characterised by very large dispersions in distance. These structures are likely those identified as strings in Kounkel & Covey (2019); Kounkel et al. (2020). However, since we do not recognise these structures as standard clusters, any further investigation of them is beyond the scope of this work.
The final cluster member selection was only performed for candidate clusters that satisfy the previous constraints. As a result of our choice of the DBSCAN input parameters (see Sect. 4.1) and of the adopted spatial configurations, a given candidate cluster can be identified by adopting similar input parameters, with possible small differences in the cluster membership. In addition, for a given pair of input parameters in two or more overlapping boxes, a given candidate cluster can be identified in more than one box (with the same membership result) if the candidate cluster is spatially small enough to be completely identified. Alternatively, it can be completely detected within one box and only partially detected in a box where the candidate cluster falls at the borders. In order to assign the most likely membership for a given cluster, we proceeded by adopting the following strategy.
We first considered the candidate clusters detected within the same spatial configuration but with different set of parameters (є, minPts). For each of the selected candidate clusters, we computed the median values of the five parameters (l, b, π,  , µδ) and then selected all the candidate clusters that were simultaneously compatible in these five parameters; that is, if the two compared distributions of each parameter overlap around the median, within half of the total width. Among the compatible candidate clusters, we selected the most populated and discarded the others. This strategy allowed us to identify the most persistent candidate clusters on different scales.
, µδ) and then selected all the candidate clusters that were simultaneously compatible in these five parameters; that is, if the two compared distributions of each parameter overlap around the median, within half of the total width. Among the compatible candidate clusters, we selected the most populated and discarded the others. This strategy allowed us to identify the most persistent candidate clusters on different scales.
In the subsequent step, we compared the candidate clusters identified in each of the five spatial configurations to select the best configuration, or, likewise, the best box in which the spatial coverage of the candidate cluster is maximised. Since we can have more than one detection of the same cluster, for each member we only selected the configuration for which it is associated with the most populated candidate cluster, and that member was removed from the less populated clusters as identified by DBSCAN. The peripheral members of candidate clusters covering a spatial region larger than the area of the box (5° × 5°), left out from the richest centred candidate cluster, were only considered as additional candidate clusters if they included at least ten elements5; the same limit was also assumed in other similar works (e.g. Castro-Ginard et al. 2018; Kerr et al. 2021). This selection strategy allowed us to also include likely members at the candidate cluster’s periphery, providing data for further investigations on the dynamics of these stellar clusters. At the end of this process, we are left with a total of 449 849 detected stars within 14 178 single candidate clusters.
Many SFRs are associated with giant molecular clouds, and thus they can have a spatial extension larger than the box of 5° × 5° used for our analysis. In order to merge candidate clusters belonging to the same complex, we proceeded as follows: we computed the median and the 16th and 84th percentiles of the distance and proper motion distributions. Then, we merged all neighbouring clusters for which distances and proper motions were compatible within 1 σ. The total number of merged clusters is 7 323.
4.3 Cluster age classification
From a visual inspection of the photometric properties of the clusters found with this analysis, we note that, while for most of the recognised clusters their selected members of any mass stay in the PMS region of the CAMD as expected, there is a fraction of recognised clusters for which only the low-mass members stay in that PMS region. This is, for example, the case of clusters with low or moderate extinction (AV ≲ 1) and ages of 10 Myr ≲ t ≲ 50 Myr, such as IC 2602, Melotte 20, NGC 2451 A, and NGC 2451 B, where part of the MS or PMS low-mass tail (MG ≳ 9) overlaps the photometric region considered here. For clusters with ages of t ~ 100–200 Myr, such as Melotte 22 (Pleiades), NGC 2422, and NGC 2516, a smaller fraction of the MS low-mass tail, likely composed of reddened members, cluster binaries or PMS members, is selected.
Further reddening effects or poorly constrained magnitudes or parallaxes can bring colours or magnitudes of members of even older clusters within the PMS photometric region considered in this work. For clusters with extinctions of AV ≳ 1, the MS of t ≳ 100 Myr old clusters in the 5 < MG ≲ 8 range fall to the right of the unreddened 10 Myr isochrone. Thus, depending on the cluster age, binaries or reddened members of clusters with ages of t > 10 Myr can also fall in the selected photometric region. Since these objects share the same proper motions and are at the same distance, they are recognised as belonging to a cluster and are therefore included in our catalogue.
To distinguish SFRs from old clusters, we adopted a pattern match procedure based on the extraction of the different patterns that characterise the observed CAMD of clusters of different ages. Among the clusters identified as described in the previous sections, we selected those listed in Table 1 (52 in total) and we used them as a template data set.
In the template data set, we identified 28 clusters, shown in Fig. 2, that we used as a proxy for clusters with ages of t ≲ 10 Myr. Such clusters were selected since most of them show a consistent luminosity spread, typical of the SFRs, starting from our brightest limit, MG = 5. However, their general shape is also set by the reddening and the distance, with the observed MG maximum limit that increases as distance decreases. All these cases have been included in the template data set to retrieve all the possible patterns observed in the CAMD due to different ages, distances, reddening, and cluster richness. For each of these clusters, we assigned an increasing flag from 1 to 28, aimed at representing the different shapes of the observed CAMD shown in Fig. 2.
We also identified eight clusters as representative of the ages 10 ≲ t/Myr ≲ 100, flagged from 29 to 36, according to the ages given in Cantat-Gaudin & Anders (2020). The observed CAMDs of these clusters are shown in Fig. 3. These clusters show an evident PMS region that is mainly populated in the range of MG ≳ 8 (e.g. NGC 2451B, NGC 2232), as per our photometric selection. Such a region becomes thinner and thinner for older clusters such as Melotte 20 and Melotte 22. Finally, we selected 16 clusters, flagged from 37 to 52 as a proxy for clusters with ages of t ≳ 100 Myr, in agreement with Cantat-Gaudin & Anders (2020). Most of these clusters have been included in the template sample to take into account the non-uniform distribution of the absolute magnitudes of their members in the observed CAMD. In fact, while for very young clusters it is uniformly populated, accordingly to their age and the IMF, the population is not entirely identified for these reddened and old clusters. For example, the clusters with flags from 43 to 52 are characterised in the CAMD by an overdensity of members with MG ≲ 9. Most of them are quite distant clusters (d ≳ 500 pc) and thus very likely affected by reddening. As shown in Appendix A, the effect of the reddening for the Gaia bands depends on the stellar effective temperature (Anders et al. 2019), and for high mass stars such an effect is greater than for low-mass stars. This would explain the presence of the peak at higher masses in the observed magnitudes of the CAMD for most of these clusters. Depending on the cluster distance, part of the low-mass tail is also detected, but the overall non-uniform pattern of their CAMD is different from that expected for young clusters. Since most of the clusters show asymmetric structures, to evaluate their extension we estimated the radius in which half of the identified members are concentrated as  , as was done in Cantat-Gaudin & Anders (2020).
, as was done in Cantat-Gaudin & Anders (2020).
In our final catalogue, we also noted the presence of other photometrically unphysical aggregates including mostly only faint stars (with G > 18.5) with very red G − GRP colours and a horizontal distribution in the CAMD likely compatible with those of giant stars and where MG is nearly constant. Since most of these peculiar clusters are in the direction of the Galactic centre, we infer that they correspond to very distant giants for which Gaia EDR3 parallaxes are systematically wrong due to the strong effects of crowding and high extinction in the direction of the Galactic centre. To separate these aggregates from SFRs or stellar clusters, we included a further 27 cases of these peculiar aggregates (flagged from −27 to −1, with a median MG from 7.6 to 15.8), covering their observed magnitude values.
According to the known ages of the clusters of the template data set, we defined the three age bins, t ≲ 10 Myr, 10 ≲ t/Myr ≲ 100, and t ≳ 100 Myr, including the clusters with flags in the [1, 28], [29, 36], and [37, 52] ranges, respectively. Then, we used a python implementation of the 2D version of the Kolmogorov-Smirnov (KS) test6, developed by Peacock (15)83) and generalised by Fasano & Franceschini (1987), to identify the most similar amongst the chosen template clusters in the CAMD for each of the 7 323 clusters; that is, the one for which the KS statistic is lowest.
The procedure is not intended to derive any best fitting parameter, but its aim is to only assign a flag to each cluster and then a “coarse” age range to which it belongs. At the end, we selected only the 1450 clusters with more than 20 members (corresponding to 302 730 objects), for which the KS test statistic is <0.2.
In conclusion, we classified 124 440 candidate YSOs that belong to 354 structures with t ≲ 10 Myr, distributed within ≲1.5 kpc. From now on, we indicate these structures as SFRs, meaning regions that can include at least one very young cluster and mostly consistent YSOs with t ≲ 10 Myr. In addition, we classified 65 863 low-mass members of 322 stellar clusters, mainly located within ~500 pc and with ages of 10 Myr ≲ t ≲ 100 Myr, and, finally, 43 936 members of 524 clusters with t ≳ 100 Myr. The objects that belong to photometrically unphysical aggregates are 68 491. The results are summarised in Table 2. From our catalogue, we reject all clusters with ages of t ≳ 100 Myr; the photometrically unphysical aggregates and those that remain unclassified are mainly poorly populated with a CAMD that does not allow us to properly classify them.
Star forming regions and stellar clusters with ages of t≲ 100 Myr are listed in Table 3, while cluster members are given in Table 47. Most of the clusters listed in the table are very extended complex regions including several sub-clusters known in the literature, merged here within single structures. Since the aim here is to detect these Galactic young structures, the literature cluster names given in Table 3, mainly taken from Cantat-Gaudin & Anders (2020) or Zucker et al. (2020) or from Simbad, are only indicative of the region.
Clusters used as template data set to select SFRs and other stellar clusters.
 |
Fig. 2 CAMD of YSOs identified in clusters with ages t ≲ 10 Myr included in the template data set. Black solid lines are the theoretical solar metallicity Pisa isochrones of 1, 10, and 100 Myr isochrones (from right to left). The number on the top right edge of each panel is the flag assigned to each cluster. |
 |
Fig. 3 CAMD of clusters with ages 10 Myr ≲ t ≲ 100 Myr, flagged from 29 to 36, and with ages t ≳ 100 Myr, flagged from 37 to 52, included in the template data set. Black solid lines are as in Fig. 2. The number on the top right edge of each panel is the flag assigned to the clusters. |
Results of the cluster age classification.
5 Results
5.1 Photometric completeness
Within the magnitude range explored in this work and assuming the restrictions on Gaia data defined in 2, the photometric cluster completeness for clusters with t ≲ 10 Myr is expected to be near 100% for non-embedded YSOs. This is because, as shown in Fig. 1, all members detectable in this age range and in the optical bands are expected to lie in the selected photometric region.
Nevertheless, the adopted restriction, RUWE < 1.4, introduced a bias in the selection of multiple members of the SFRs. To estimate the fraction of missed binary members with the Gaia-based selection used in this paper, we used the Taurus-Auriga binary-star list by Kraus et al. (2012) as a reference. Details about the comparison of this list with our catalogue and Gaia EDR3 data are given in Appendix B. This comparison shows that, due to the RUWE restriction, in SFRs at distances similar to Taurus-Auriga, we have lost about 72% of their binary populations. Assuming a binary frequency of ~50% (Mathieu 1994), a loss of ~35% of PMS members can be expected. However, at large distances, the projected binary motions become smaller, and therefore we expect a less significant binary member loss for the farther-out SFRs.
For clusters with ages of t ≳ 10 Myr, the cluster completeness decreases with ages and strongly depends on the cluster distance. In fact, clusters with 10 Myr ≲ t ≲ 100 Myr (indexed from 29 to 36), are mainly in the solar neighbourhood (d < 500 pc). For these clusters, even though we are not able to detect the entire cluster population, we are, however, able to detect part of the very-low-mass tail component. The fraction of the detected very-low-mass tail component decreases with age, and, for clusters with t ≳ 100 Myr (indexed from 37 to 52), mainly concentrated at d ≳ 500 pc, the completeness is very low. The latter were discarded from our final catalogue since they include only a small fraction of the cluster members and are not in the age range of interest for this work. Clusters with ages of 10 Myr ≲ t ≲ 100 Myr are included in our catalogue since the age transition to the clusters with t≲10 Myr is not sharply defined, and, in addition, there are structures such as Sco OB2 that include clusters in both age ranges that very likely belong to correlated star forming processes.
5.2 Spatial distribution
Figure 4 shows the maps of the 124440 YSOs associated with the 354 SFRs with ages t ≲ 10 Myr, while Fig. 5 shows the maps of the 65 863 stars associated with the stellar clusters with ages of 10 Myr ≲ t ≲ 100 Myr. Each map has been obtained as a 2D histogram smoothed with a Gaussian kernel at 3σ, adopting a pixel size of 3 pc × 3 pc.
Most of the overdensities in Fig. 4 are associated with known SFRs, some of which are labelled in the figure. With the exception of those within 200–300 pc, all clusters present a radial, elongated shape, tracing the increasing uncertainties in the distances.
The clusters with ages of 10 Myr ≲ t ≲ 100 Myr are mainly limited within ~600 pc (see Fig. 5) and show a much more diffuse spatial distribution. Very rich clusters such as NGC 2232, NGC2451B, Gamma Velorum, NGC 2547, NGC 2516, and Alessi5 at distance of ~400 pc, seem to belong to a common giant complex, mostly lying in the third Galactic quadrant.
5.3 Literature comparison
In this section, we present the comparison of our results with those previously obtained in the literature for two particular regions, Sco OB2 and NGC 2264. These comparisons were used to estimate our completeness and the contamination level, at least when the completeness of the comparison sample enabled us to do so. We note that we considered each of the merged clusters as a unique ensemble. A detailed sub-clustering analysis, with the identification of possible sub-structures with age-gradient or kinematic sub-clusters is deferred to a future paper. A detailed comparison with the literature for other SFRs is presented in Appendix C, where we also compare the whole catalogue with other all-sky catalogues, mainly derived with Gaia DR2 data.
5.3.1 The Sco-OB2 association
The Sco-Cen or Sco-OB2 association is a very extended SFR (~120° × 60°) quite close to the Sun (d ~ 150 pc), which, in the last years, has been the subject of several studies focussed on the low-mass population. By exploiting available all-sky surveys, these studies finally allowed us to study the entire region and its complexity (e.g. Zari et al. 2018; Damiani et al. 2019; Kounkel & Covey 2019; Kerr et al. 2021; Luhman 2022).
We spatially selected the members of this region by considering all stars with −102° < l < 10°, −30° < b < 40°, and, as assumed in Damiani et al. (2019), a distance of d < 200 pc. This gave a total of 9 663 YSOs with ages t ≲ 100 Myr, distributed as in Fig. 6. In the (l, b) plane, the pattern of the YSOs associated with Sco-OB2 is that already found in the literature (e.g. de Zeeuw et al. 1999; Damiani et al. 2019; Kerr et al. 2021). Among the selected objects, 4232 YSOs have been classified in the t ≲ 10 Myr range. 2 472 are concentrated in the upper Sco (US) region. They correspond to the youngest sub-population of Rho Ophiuchi. Another prominent sub-population, classified in the 10 Myr ≲ t ≲ 100 Myr (flag 31) range, includes 3 741 YSOs falling in the upper Centaurus-Lupus (UCL) and lower Centaurus-Crux (LCC) regions. This represents the first generation of stars of the Sco OB2 region, in agreement with recent results (e.g. Damiani et al. 2019); Luhman 2022).
Proper motions, parallaxes, and the CAMDs of the different sub-populations detected in the Sco OB2 association are shown in Fig. 7. The proper motions of the YSOs associated with Sco-OB2 show a quite complicated pattern, confirming the complex kinematic structure of this association. The values of parallaxes of YSOs in Sco-OB2 are mostly enclosed between ~5 mas and ~ 10 mas, corresponding to a mean distance of 152 pc and standard deviation σ = 28 pc. Finally, in the CAMD, we can recognise a usual distribution of YSOs in the PMS region. As already noted, the census of the first-generation stars of the Sco OB2 association is likely incomplete since it is expected to lie in the region of the CAMD that has not been considered in this work.
To estimate the completeness level of our census, we compared our list of Sco-OB2 YSOs with the ones recently published by Damiani et al. (2019) and Kerr et al. (2021), based on Gaia DR2 data, and by Luhman (2022), based on Gaia EDR3 data. To perform these comparisons, we used the Gaia identification number of YSOs in our catalogue, retrieved as described in Appendix C.4. We find that there are 6 492 YSOs in common with the Damiani et al. (2019) catalogue, which includes a total 10 839 members. That is about 60% of the Damiani et al. (2019) list. Among the 9663 YSOs we selected in the Sco-OB2 association, 7553 fall in the spatial region and magnitude range of G < 19.5 covered by Damiani et al. (2019). Therefore, the objects in common are 86% of our sample in the same field. Many of the remaining 1061 YSOs (14%) not selected by Damiani et al. (2019) show a spatial distribution consistent with that of the other members, and thus we discard the hypothesis that they are contaminants and suggest that they are likely YSOs missed by Damiani et al. (2019; i.e. those based on the less complete Gaia DR2 catalogue).
Adopting the same spatial constraints, we retrieved 9 083 objects in the Sco-OB2 region that were selected as candidate YSOs in the Kerr et al. (2021) catalogue, independently from their clustering type of classification. Among these, 5203 are in common with our catalogue, but those classified as YSOs are 5109; that is, ~56.2% of the Kerr et al. (2021) sample8.
The Luhman (2022) catalogue includes a total of 10 509 YSOs; however, to be consistent with our selection, we selected those with Mg > 5, 7.5 < G < 20.5, RUWE < 1.4 (7925 in total). Using the Gaia EDR3 ID and considering the 7408 counterparts falling in the region covered by Luhman (2022), we found that 6341 YSOs are in common with our catalogue, representing 80% of the Luhman (2022) catalogue and 85.6% of our list of YSOs in the Sco Cen.
These percentages cannot be used to accurately estimate our level of completeness or contamination, since the catalogues were obtained starting from different initial constraints, both for the photometric and the astrometric selection, which can inevitably introduce several biases. However, these comparisons are useful to confirm membership for ~85% of the selected members. The remaining 1067 objects not retrieved by Luhman (2022) but selected by us as YSOs show a spatial distribution consistent with that of the other members with two strong concentrations of them in the US region and around V 1062 Sco. We therefore conclude that they are genuine members rather than contaminants, which were likely missed by Luhman (2022) in the photometric selection based on the GBP − GRP colours.
 |
Fig. 4 Density map of three orientations of the GP of YSOs associated with SFRs with ages of t ≲ 10 Myr. In the upper left panel, the Sun is at (0, 0), the x-axis is directed towards the Galactic centre, and the y-axis is towards the direction of the Galactic rotation. Dashed white circles are drawn at distance steps of 500 pc. In the upper right and lower left panels, the z-axis is perpendicular to the GP. Colour bars indicate the surface densities, that is, the number of stars per bin and per pc2. Some known SFRs are indicated. The numbers from 1 to 9 in the upper right and bottom panels indicate the position of the clusters indicated in Fig. 5 (upper left panel). |
 |
Fig. 6 Spatial distributions in Galactic coordinates of YSOs associated with the Sco-OB2 Association. The de Zeeuw et al. (1999) sub-regions of US, UCL, LCC are shown. The different colours indicate all the different substructures found in this region. |
5.3.2 The Monoceros OB1/NGC 2264 complex and the Rosette nebulae
Another well-studied region that we used to test our results is the cluster NGC 2264 in the Monoceros OB1 complex. This relatively compact and close (~720 pc from the Sun) SFR, devoid of background and foreground emission, has been the subject of many detailed studies, including, for example, X-ray observations (Flaccomio et al. 2006), optical and near-IR analysis of its low-mass population (Venuti es al. 2019), and coordinated synoptic investigations with optical and IR light curves with CoRot and Spitzer (Cody et al. 2014). Flaccomio et al. (in prep.) compiles the most complete data set of NGC 2264, based both on all-sky surveys (Gaia EDR3, 2MASS, VPHAS) and dedicated observations falling in the 98.93° < RA < 101.47° and 8.45° < Dec < 10.95° regions. The young structure we identified in this field includes a total of 1916 YSOs, but only 1062 of them (~55%) fall in the region investigated by Flaccomio et al. (in prep.). The remaining YSOs are in part (404 YSOs) concentrated in the region corresponding to the cluster IC 446, while a further unknown group of 450 YSOs are sparsely distributed in the southern region of NGC 2264. As shown in Fig. 8, a sub-group of the latter form a visual bridge along a filamentary structure, which is clearly visible in the IR IRIS image, down to the location corresponding to the more distant Rosette nebula, which is located at ~1.5 kpc and hosts the SFR NGC 2244. Thus, our finding is that the known cluster NGC 2264 actually belongs to a structure larger than the ~2° × ~2° region, typically considered in the literature for this SFR. The mean distance of YSOs associated with the complex NGC2264-IC 446 is 731.86 ± 95.5 pc, even though the proper motion distributions of the three subgroups suggest they share similar but not equal values9.
In the same region, we identified a further five sub-structures with distance >0.5 kpc10, the most populated being the cluster in the CMaOB1 association, centred around RA = 106.3° Dec = −11.47°. It is found at a distance of 1250 ± 162 pc, is associated with the reflection nebula IC 2177, and includes 1709 YSOs. In addition, we identified the cluster NGC 2244, which includes 810 YSOs, is centred at RA = 98.3° Dec = 4.9°, and is at a distance of 1580 ± 199 pc. We also identified the cluster associated with Mon R2, which is at a distance of 897 ± 112 pc and includes 1272 YSOs. In addition, we detected the cluster indicated in Cantat-Gaudin & Anders (2020) as UPK 436 with 620 members and a minor sparse cluster in the region of CMaOB1 located at 807 pc. Figure 9 shows the PM, parallaxes, and CAMD of all these sub-structures, where it is clearly visible that they are spatially and kinematically uncorrelated, while in the PMS region of the CAMD they are indistinguishable since they consist of similarly aged stars.
The membership defined in Flaccomio et al. (in prep.) includes two confidence levels. One is based on the combination of several criteria derived by dedicated X-ray, spectroscopic, and IR observations, including 2263 confirmed members (sample C). Moreover, the fraction of false positives is negligible. Another list (sample C-Wide) is based exclusively on all-sky surveys and includes 1542 YSOs. The membership was deduced by a smaller number of criteria, and thus the number of false positives is expected to be higher. We find that 972 (960) YSOs of the sample C (sample C-wide) are in common with our list of YSOs in the NGC 2264 region, corresponding to a fraction of 43% (62%) with respect to the Flaccomio sample. These fractions are considered here as indicators of our level of completeness of the entire SFR population. However, these results are strongly conditioned by the starting photometric selection (Mg > 5) and the restrictions on the Gaia EDR3 data that we adopted in this work. In addition, the Flaccomio et al. (in prep.) sample C includes 497 of the 2263 confirmed members that do not have a Gaia counterpart.
To estimate the efficiency of our method in recovering YSOs, we considered the members selected by Flaccomio et al. (in prep.) with a Gaia counterpart, which fall in the photometric region considered in this work and are compliant with our initial data restrictions (i.e. RUWE < 1.4 and parallax relative error <0.2). Adopting this sample, the fraction of the YSOs we selected in common with the Flaccomio et al. membership is 95–96%, considering both the samples C and C-Wide. We note that this is the efficiency of our clustering method but is not the efficiency of the Gaia data. In fact, if for the two lists we consider the members falling in the same photometric region but we do not consider the restrictions in RUWE and in the parallax error, the fraction of YSOs in common is 72% for sample C and 77% for sample C-wide. This suggests that we missed 23-28% of genuine YSOs due to remaining issues in the Gaia data, at least in the current Gaia EDR3 release.
Finally, we find that among the 1052 YSOs we selected in the NGC 2264 region, a total of 1034 are included in the list of objects collected by Flaccomio et al., but 62 of them are not members in the more complete and less contaminated sample C. This means that about 92% (i.e. (1034–62)/1052) of the YSOs we selected are confirmed members. Hence, we conclude that the contamination level of the sample that we selected is ~8%.
For comparison, Kounkel & Covey (2019)) found 637 YSOs belonging to the clusters named as Theia 41 and 189 in the same region, with 548 and 89 objects, respectively. Of them, 420 (about 66%) are in common with our list.
 |
Fig. 7 Proper motions in RA and Dec, parallaxes, and CAMDs of the groups of YSOs associated with the Sco OB2 association. The symbol colours are as in Fig. 6. Three representative solar metallicity isochrones from the Pisa models are also shown as solid lines in the right panels. |
 |
Fig. 8 Spatial distribution in equatorial coordinates of the YSOs associated with NGC 2264, NGC 2244, Mon R2, CMA OB1, and UPK436. YSOs are overplotted on an IRIS 100 µm image (Miville-Deschênes & Lagache 2005). For clarity, Orion members have not been plotted. |
6 Discussion
In the previous sections, we describe how overdensities in the 5D parameter space (l, b, π, 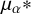 , µδ) were identified, starting from a photometrically selected sample that covers the expected PMS region of YSOs with ages t < 10 Myr. Since no attempt has been made to correct for interstellar reddening, the starting sample was also contaminated by older reddened stars. Another possible reason for the contamination of older stars is derived from the adopted strategy to select the starting sample in the Mg versus G − Grp plane, where the sensitivity to stellar ages of the available isochrones is quite low for the low-mass population. In fact, for faint and very-low-mass stars, isochrones become closer and closer for ages over about 50–100 Myr, and, consequently, it is difficult to separate young populations from older ones. As a result, the DBSCAN clustering algorithm, adopted to resolve spatially concentrated and/or co-moving stellar populations located at the same distance, can also select clusters older than 10 Myr.
, µδ) were identified, starting from a photometrically selected sample that covers the expected PMS region of YSOs with ages t < 10 Myr. Since no attempt has been made to correct for interstellar reddening, the starting sample was also contaminated by older reddened stars. Another possible reason for the contamination of older stars is derived from the adopted strategy to select the starting sample in the Mg versus G − Grp plane, where the sensitivity to stellar ages of the available isochrones is quite low for the low-mass population. In fact, for faint and very-low-mass stars, isochrones become closer and closer for ages over about 50–100 Myr, and, consequently, it is difficult to separate young populations from older ones. As a result, the DBSCAN clustering algorithm, adopted to resolve spatially concentrated and/or co-moving stellar populations located at the same distance, can also select clusters older than 10 Myr.
A pattern match procedure has been adopted to disentangle SFRs and young clusters from older and photometrically unphysical clusters. We found 354 SFRs with ages of t ≲ 10 Myr and 322 young clusters with ages of approximately 10–100 Myr. We now discuss these validated findings in the context of the GP structure within ~1.5 kpc of the Sun. The maps of the young stellar clusters recognised by the DBSCAN clustering algorithm, most of them already known in the literature, are shown in the previous sections, and specific spatial and kinematic details are presented for some of them.
To identify clusters extended on scales larger than the 5° × 5° boxes used in the analysis, we merged adjacent clusters with consistent proper motions and distances. This procedure has been applied to identify extended SFRs as a whole, as in the case of the Orion complex or Sco OB2 UCL, with r50 equal to ≃17° and ≃15°, respectively, which are among the most extended structures resolved in this work. In several cases, it identifies clusters that encompass multiple populations, as in the case of NGC 2264, which was identified as a unique structure also including the close cluster IC 446 and other YSOs in the surrounding region. A more in-depth analysis of the two clusters shows that their proper motions can be distinguished into slightly different sub-populations. Thus, our overall procedure used to define clusters tends to include multiple sub-populations sharing similar properties, which are likely associated with the progenitor molecular cloud.
The question of cluster and sub-cluster identification is a very complex issue that can be dealt with at the different spatial precision levels required for a given analysis. This was done, for example, for the MYStiX project in Feigelson (2018), where a parametric statistical regression approach providing hierarchical ellipsoid structures was adopted. The evidence of a wide range of central surface densities found in the MYStIX maps is in agreement with the different spatial morphology of the SFRs identified in this work.
Figure 10 shows the spatial distribution of the young stellar clusters found in this work in three different distance bins: [100, 600] pc, [600, 2000] pc, and [100, 2000] pc. The young clusters are drawn by distinguishing them in the age bins t < 10 Myr, 10 Myr < t < 100 Myr, and t < 100 Myr. We note that clusters with 10 Myr < t < 100 Myr were only found in the solar neighbourhood (<600 pc) and thus are only shown in the [100, 600] pc distance range.
The distribution of SFRs (t < 10 Myr) within 600 pc is dominated by the presence of big young structures crossing the GP such as the Orion and Perseus complexes, Gamma Velorum (Pozzo 1), and Lac OB1, which are under the GP, BH 23 (corresponding to Theia 80 in Kounkel & Covey 2019); and RSG 8, which is close to the GP, Serpens, Alessi 62, Collinder 359, and Rho Ophiuchi (over the GP). The clusters with ages of 10 Myr < t < 100 Myr in the same distance range definitely appear more diffuse. Apart from the well-known Sco-Cen association covering ~60° in longitudes, we detected the similarly huge association in the Vela-Puppis region as a unique complex, including Trumpler 10, γ Velorum, NGC 2457, and NGC 2451B, as well as the associations around NGC 2232, Roslund 5, and Alessi 19. Their positions appear to be connected to the clusters with t < 10 Myr since they follow a spatial pattern crossing or one very close to that of the SFRs. This suggests that they likely belong to a common star formation process encompassing at least two generations of YSOs, with the first generation including extended populations of dissolving young clusters and associations.
The large Sco-Cen association is connected to the Vela and Orion complexes, confirming what was already found by Bouy & Alves (2015) with Hipparcos data. These three regions are described there as three large-scale stream-like structures.
Going towards larger distances (d > 600 pc), the SFRs show a more regular pattern, which is approximately parallel to the GP. The most prominent SFRs are ASCC 32 and Cep OB3b in the Cepheus, respectively under and over the GP at a distance of ~800–900 pc. Among the most distant SFRs with more than 300 members and distances ≳1400 pc, we detected NGC 2244, NGC 6530, NGC 6531, NGC 2362, and FSR 0442.
The overall distribution of YSOs in SFRs with d ≲ 600 pc traces a complex 3D pattern in the solar neighbourhood. In particular, in the Z versus X edge-on Galactic projection (see bottom left panel in Fig. 4 and top left panel in Fig. 10) we find evidence of a projected inclined structure, mainly traced by the Orion, Vela OB2, and Rho Ophiuchi star forming complexes in the third and fourth Galactic quadrants and by the Serpens, Lacerta OB1 and Perseus in the first and second Galactic quadrants. However, the SFRs falling in the Cepheus region do not follow this pattern. A global view of these structures and their spatial correlation with the surrounding nebular emission suggests a pattern consistent with the results found in Molinari et al. (2010), where massive proto-clusters and entire clusters of YSOs in active SFRs are associated with clouds that collapse into filaments.
As already found in Zari et al. (2018), current data reveal a very complex 3D structure that cannot be simply described with the Gould Belt, that is, the giant flat structure inclined by ~20° with respect to the GP, first pointed out by Gould (1879). This insight was already suggested by Guillout (2001), who presented the first detection of the Gould Belt late-type star population and proposed the alternative scenario of a Gould disc.
A more detailed representation of the young Galactic component in the Solar neighbourhood was recently proposed by Alves et al. (2020), who determined the 3D distribution of all local cloud complexes by deriving accurate distances to about 380 lines of sight. They suggested that such 3D distribution could be described by a damped sinusoidal wave, which they call the Radcliffe wave, with an amplitude of ~160 pc and a period of ~2 kpc. It crosses Orion (around a minimum), Cepheus (crest), North America, and Cygnus X. This structure is separated and distinct from a second structure, indicated as a “split”, crossing the Sco-Cen, Aquila, and Serpens clouds. They propose that the Gould Belt is a projection effect of two linear cloud complexes. The spatial distribution of YSOs associated with SFRs that has been identified in our work shows much more complex and diffuse structures, but the two elongated linear structures suggested by Alves et al. (2020) approximately cross the borderline of the two separated structures visible in the X, Y map of Fig. 4, delimited by the SFRs indicated by Alves et al. (2020). This leads us to confirm that the local young Galactic component is very complex. While our data are broadly consistent with the Alves et al. (2020) findings, further investigations, including a more detailed analysis of the kinematics of the structures based on the 3D space coordinates (X, Y, Z) and velocities (U, V, W; e.g. de Zeeuw et al. 1999), are required to confirm the scenario and to find additional insights regarding their origin.
To gain further insights concerning the star formation history of the SFRs, it is crucial to derive more accurate stellar ages. However, we do not attempt to derive stellar ages of the selected YSOs for several reasons. First of all, we lack a suitable photometric system. In fact, the large Gaia EDR3 G and RP photometric bands used for this work are not sensitive to the fundamental stellar parameters (effective temperatures, stellar ages, etc.), especially for low-mass stars. However, future Gaia releases, overcoming issues related to the BP bands at faint magnitudes, could be crucial to this aim. Secondly, we lack the spectroscopic data needed to derive individual stellar reddening values to appropriately place these YSOs on the HR diagram. Alternatives such as the use of 3D reddening maps (e.g. Bovy et al. 2016; Lallement et al. 2019) require careful analysis, since the integrated extinction tends to be underestimated in the molecular clouds, where SFRs are typically located. A detailed analysis is deferred to future works based on the combination of Gaia and spectroscopic data from available surveys, such as Gaia-ESO (Gilmore et al. 2012; Randich et al. 2013), LAMOST (Zhao et al. 2012), or APOGEE (Majewski et al. 2017), or future surveys such as WEAVE (Dalton et al. 2012) and 4MOST (Guiglion et al. 2019).
 |
Fig. 9 Proper motions in RA and Dec, parallaxes, and CAMDs of the SFRs falling in the field of view of NGC 2264. The symbol colours of the clusters are as in Fig. 8. Three representative solar metallicity isochrones computed from the Pisa models are also shown. |
 |
Fig. 10 Aitoff projections in Galactic coordinates of the YSOs in the different age bins (t < 10 Myr, 10 Myr < t < 100 Myr and t ≲ 100 Myr), with distance in the range ([100, 600] pc (left panels), [600, 2000] pc (mid right panel) and [100, 2000] pc) (upper and bottom right panels). Colour codes indicate stellar distances. |
7 Summary and conclusions
We used the machine learning unsupervised clustering algorithm DBSCAN to systematically identify all SFRs with ages of t ≲ 10 Myr within ~ 1.5 kpc of the Sun. The density-based clustering algorithm was applied to the Gaia EDR3 positions, parallaxes, and proper motions of a photometrically selected starting sample.
A pattern-match procedure based on a template data set including typical clusters detected within the photometric sample was used to distinguish very young clusters from the contaminant old clusters and from photometrically unphysical clusters. We provide here a catalogue with the main parameters (positions, spatial extent, median distance and number of members) of the 354 SFRs with ages of t ≲ 10 Myr. The parameters of the 322 young clusters with ages of 10 Myr ≲ t ≲ 100 Myr are also given. We also provide the list of 124 440 and 65 863 YSOs found in the SFRs and the young clusters, respectively, mainly including late-type K-M stars. A substantial number of YSOs have been recognised for the first time. Based on the comparison of our list of YSOs in the well-known Sco-Cen region and in NGC2264, we roughly estimate that within our observational limits the completeness of the census of cluster members obtained with our analysis is ≳85%, at least in very rich and concentrated SFRs. For low-density regions, such as the Taurus-Auriga association (see Appendix C), this completeness figure is expected to be around 50%. The mass-function coverage of each cluster strongly depends on the cluster distance and is set by the observational limit. Compact regular clusters and SFRs in large complexes such as Taurus, Orion, Sco-OB2, Perseus, and Cygnus, were identified with a high level of efficiency, as estimated from the comparison with other available catalogues (see Appendix C).
The overall distribution of these clusters in the Galaxy context shows that they are distributed along a very complex 3D pattern that seems to connect them at least within 500–600 pc. Outside of this distance, the clusters appear to be more regularly and closely distributed along the GP.
As far as we know, the catalogue of YSOs presented in this work is the sole all-sky catalogue based on the most recent Gaia EDR3 data, which benefit from major improvements with respect to Gaia DR2. This catalogue represents a step forwards in the census of SFRs and can be used, for example, for further detailed interpretations of their spatial distribution in the context of the spiral arm model (Reid et al. 2019), since it covers a substantial region crossed by the Local Arm and, marginally, some regions of the Perseus and Sagittarius-Carina arms (Poggio et al. 2021). Future and photometric deep surveys, such as the Rubin Legacy Survey of Space and Time (LSST) will allow us to extend these limits.
We note that at this stage these results are not suitable for studies of IMF, star formation history or cluster dynamics, those based on the full space 3D velocity determination, since the census of the SFRs is not complete, and accurate masses and ages, as well as radial velocities can not be determined, until further data are available. Nevertheless, the dominant component of the SFRs has been detected, and thus these results can be used as driving samples for the extraction of complete populations from Gaia data by relaxing the stringent constraints adopted in this work. Finally, the SFRs identified in this work are defined well enough to allow detailed studies of circumstellar disc evolution and direct imaging of young giant planets based on multi-band analyses of available or future additional observations (X-rays or IR or radio) targeting some of the individual clusters.
Acknowledgements
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. E.T. acknowledges Czech Science Foundation GACR (Project: 21-16583M). J.M.A. acknowledges financial support from the project PRIN-INAF 2019 “Spectroscopically Tracing the Disk Dispersal Evolution”. The authors are very grateful to the anonymous referee, for providing constructive comments and suggestions which significantly contributed to improving this publication.
Appendix A Interstellar reddening effects
In this section, we show the effects of the reddening on the sample selected as described in Section 3. As discussed in Anders et al. (2019), for a generic pass band, i, the extinction coefficients Ai/AV depend on the stellar effective temperature. The subsequent dust-attenuated photometry of very broad photometric passbands, such as the Gaia EDR3 ones, is not simply a linear function of AV. It is also a function of the source spectrum that is its effective temperature.
The PARSEC 1.2S stellar models (Bressan et al. 2012; Chen et al. 2014; Tang et al. 2014) have been implemented to predict tracks and isochrones also at non-zero extinction. As done in Montalto et al. (2021), in order to have an indication of the reddening that affects our data, we used the CMD 3.3 input form web interface, and we constructed a grid of stellar models assuming the 1 Gyr isochrone and AV=[0.1, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 20.0, 30.0].
Figure A.1 shows how the 1 Gyr isochrone changes by increasing extinction, AV, from 0 to 10, in the CAMD obtained by adopting the different Gaia colours (panels a and b). The 1 Gyr isochrone at AV = 0 is highlighted by a thick black line, while the 1 Gyr isochrone at Av = 3 is highlighted by symbols with different shades of pink in the different stellar evolution phases.
We note that the reddened isochrone is not linearly shifted along a reddening direction, which usually happens when adopting a reddening vector. For example, for an object at Mg = 3, corresponding to a star with (Gbp-Grp)0=0.47, (G-Grp)0=0.30, an effective temperature of 6930 K at 1 Gyr (black empty square in the Figure), and an extinction of AV = 3, the reddening E(Gbp-Grp) is equal to 1.24 and E(G-Grp) is equal to 0.55 (blue arrows in the Figure). However, for an object at MG = 8, corresponding to a star with (GBp-Grp)0=1.81, (G-Grp)0=0.90, effective temperature of 3945 K at 1 Gyr (black bullet in the Figure), and an extinction of AV = 3, the reddening E(Gbp-Grp) is equal to 1.09 and E(G-Grp) is equal to 0.26 (red arrows in the Figure). Thus, at different temperatures, and for a fixed AV, the shift in colour due to the reddening is smaller for the colder star. This effect is higher in the G versus G-Grp diagram, as can be deduced from the different slopes of the blue and red arrows. In this case, for a ~4000 K star, the E(G-GRP) value (equal to ≃0.26) is about half of that (≃0.55) associated with a ~7000 K star. This implies that while a reddened 1-Gyr-old star with an effective temperature of ~ 7000 K can be expected to be found in the PMS region and mimic a star younger than 10 Myr, a colder star of ~4000 K, of the same age, and affected by the same extinction, does not fall in the PMS region (see Fig. A.1, panel b). In conclusion, the effect of uncorrected reddening in terms of contamination of our initial photometric sample by old stars is larger for stars of spectral type F and G than for K and M stars.
 |
Fig. A.1 PARSEC 1 Gyr isochrone at solar metallicity with extinction, AV, ranging from 0 to 10.0 in the CAMD obtained by adopting the different Gaia magnitudes (black dots). The 1 Gyr isochrone at AV = 0 is highlighted by a thick black solid line. The 1 Gyr isochrone at AV = 3 is highlighted by pink coloured lines of different shades during the red giant branch (RGB), asymptotic giant branch (AGB), red clump (RC), sub-giant (subGig), and MS phases. The red, light-blue, and green solid lines are the 1, 10, and 50 Myr Pisa isochrones at solar metallicity. The empty square and the bullet in each panel represent a star of 6930 K and 3945 K, respectively, while the blue and red arrows are the reddening vectors corresponding to AV = 3, for these two representative stars (see text). |
Appendix B Effect of binarity or multiplicity on astrometric selections
At the level of astrometric sensitivity offered by Gaia, the orbital motions of binary (or multiple) stars sometimes become measurable, and also difficult to disentangle from proper motion. This holds both for resolved pairs and for unresolved, unequal-mass pairs where the photocentre displays significant motion (see Kervella et al. 2022). If the binary period resonates with the Gaia sampling frequency, parallax measurements will also be affected. Perhaps the best-studied star-forming region in terms of its binary-star population is Taurus-Auriga, and we refer the reader to the review by Mathieu (1994) for a perspective of the expected range of system parameters. Taurus is one of the few SFRs where lunar occultation techniques were feasible for the detection of close pairs, down to separations of 0.009″(Mathieu 1994, Table A1 and references therein). Therefore, the projected binary separations span a factor of ~ 1000, with no ‘typical’ value. Correspondingly, their orbital periods span a range of a factor of ~ 30000.
 |
Fig. B.1 Diagram of RUWE values versus the Gaia colour GBP–GRP of the Kraus et al. (2012) Taurus-Auriga binary-star list with Gaia EDR3 counterparts. Filled symbols are the binaries also selected in this work, while empty symbols are those rejected. |
We empirically checked if the Gaia-based selection used in this paper keeps the binary members of an SFR by matching the Taurus-Auriga binary-star list in Table 1 from Kraus et al. (2012) with the Gaia EDR3 catalogue and its subset selected in this paper. Out of 156 stars in Kraus et al., we found 142 Gaia-EDR3 counterparts within 0.5″, 40 of which were selected in this work using DBSCAN.
We then compared the RUWE distributions of the selected versus unselected systems to gain insight into how binary motions impact RUWE and the subsequent selection. Figure B.1 shows a diagram of RUWE versus Gaia colour Gbp–Grp. The horizontal line indicates our maximum accepted RUWE value. Filled symbols are stars passing our selection, while empty symbols are the unmatched binaries, that is, those not retrieved in our catalogue. It should be noted that the cut in absolute-G magnitude rejects some stars that would have passed the RUWE constraint. Nevertheless, the vast majority of unmatched stars indeed have RUWE values well above the chosen limiting value and were likely rejected for this reason. There is little or no dependence of RUWE on Gaia colour, and therefore mass (although part of colour spread is also due to high extinction towards Taurus-Auriga). Also interesting is the diagram in Fig. B.2 showing RUWE versus binary separation. Here, the absence of any dependence of RUWE on projected separation (when measurable) is very evident, including unresolved pairs, where only the photocentre is affected by orbital motion. This latter diagram only contains six out of 40 stars selected by us, since about half of the Kraus et al. pairs are spectroscopic binaries with no measured separation. We also point out that out of the 76 binaries with no measured separation, 32 pass our selection (42%), while only eight out of the 66 binaries with measured separation pass the selection (12%), probably because photocentre motion has a smaller effect on astrometry compared to the motion of resolved components. Overall, extending this result from Taurus-Auriga to other SFRs at similar distances, we would predict a loss of ~ 72% of their binary populations due to our selection criteria. Thus, if a binary frequency is as high as 50% (Mathieu 1994), a loss of ~35% of PMS members can be expected. However, since this work selects stars at distances up to ~1500 pc, this estimate should not be naively extended to our whole sample: the larger the distance, the smaller the projected binary motions, and hence, the closer they are to our detection limit. We therefore expect a less significant binary member loss for the farther-out SFRs. A more detailed study of these effects would, however, be far beyond the scope of this paper; one must also take into account that the new Gaia data release DR3 contains orbital astrometric solutions for 135 760 non-single stars11.
 |
Fig. B.2 Diagram of RUWE values versus the binary separation of the Kraus et al. (2012) Taurus-Auriga binary-star list with Gaia EDR3 counterparts. Symbols are as in Fig. B.l. |
Appendix C Literature comparison
C.1 Taurus-Auriga association
The Taurus-Auriga complex is one of the nearest active SFRs of low-mass stars, to which many works have been dedicated. In this region, we identified several sub-structures, as can be seen from Fig. C.1. In order to identify the YSOs associated with the Taurus-Auriga association, we imposed the upper distance limit equal to 225 pc, as was done in Krolikowski et al. (2021), and restricted the spatial region in the ranges of 58.0°< RA <86.0° and 10.5° < Dec < 38.5°. We considered the sub-structures whose members are all within these limits. With these conditions, we identified a total of 313 YSOs associated with six sub-structures. The spatial distributions are shown in Fig. C.1, while proper motions, parallaxes, and the CAMD are shown in Fig. C.2.
The members in the southwest sub-region (light blue plus symbols in the figures) are distributed quite close to the 10 Myr isochrone; thus, they could be part of an older population not selected by us for the photometric cut we used. However, with the exception of this, the members of the other sub-structures show the typical distribution of stars in PMS. The proper motions of the sub-structures are quite well distint, as well as parallaxes, suggesting a complex 3D structure with the known core including members in the 63.0° ≲ RA ≲70.0° region and 23° ≲ Dec ≲28° (blue star symbols in the Figures) also being on the close side (median distance equal to 132 pc). The easternmost and most populated sub-structure (red square symbols in the figures) is instead the most distant (median distance equal to 171 pc). Marginal evidence of age spread, as found in Krolikowski et al. (2021), is also found with our analysis, but our results cannot be considered conclusive as they are based on reddening-uncorrected photometry.
Krolikowski et al. (2021) very recently compiled the most complete and inclusive census of members of this region found in the literature. Among these, 587 objects have Gaia EDR3 counterparts, with 528 having a full astrometric solution. Using the Gaia EDR3 identification number given in the Krolikowski et al. (2021) table, we matched the list of the 437 Taurus members in the Krolikowski et al. (2021) table that are included in the photometric limits imposed in our work with the YSOs with t < 10 Myr (i.e. classified with flag from 1 to 28), and we found 202 objects in common, which amounts to about 46% (202/437) of the Krolikowski et al. (2021) list and 65% (202/313) of our list of YSOs in this region. We note that the Krolikowski et al. (2021) list was obtained from the compilation of previous works, including local spectroscopic and IR data surveys that do not homogeneously cover the entire region as we have done with Gaia data. For example, many of the 111 YSOs not included in the Krolikowski et al. (2021) table belong to clusters 579 and 572 in Table 3, which includes 88 and 30 YSOs, respectively (red squares and light blue symbols in Fig. C.1, top panel), in two sub-regions poorly covered by Krolikowski et al. (2021).
We also compared the list of YSOs in Taurus with the list of members identified as excess of mass (EOM) by Kerr et al. (2021) using Gaia DR2 data. Details on the match with our catalogue are given in Sect. C.4. As in our case, Kerr et al. (2021) found sub-structures beyond the distance of known members. To perform a consistent comparison, we restricted the Kerr et al. (2021) catalogue in RA, Dec, and distance, as was done for our catalogue. 429 were identified as EOM in this region. Among these, we considered the ones with G > 7.5 and MG > 5 to match the same photometric region adopted for our catalogue. Of the 409 Kerr et al. (2021) YSOs that meet these conditions, we found that 197 (about 48%) are in common with our list of YSOs. We note that a rigorous consistent comparison is very hard to perform, since it strongly depends not only on the adopted clustering techniques but also on the sub-sample of Gaia data that is selected as starting point of the subsequent analysis.
The Taurus region is a well-known complex structure in which the membership has been very hard to achieve due to its large spatial extent and strong obscuration by the nebula. The comparison we made is sufficient to assert that about 50% of the selected YSOs in this region are already found in other surveys and that they are distributed in sub-structures that are consistent with those found in other works, and in particular with the results presented by Kerr et al. (2021), which homogeneously cover the entire region.
C.2 Orion complex
Young stellar objects associated with the Orion complex have been identified by selecting objects with 75° < RA < 90° and −11°< Dec < 10°. In this way, we found 18 840 YSOs associated with seven sub-structures with t ≲ 10 Myr. These are shown in Fig. C.3 12, where we note the presence of already known substructures such as λ and σ Ori, ONC, and 25 Ori. All the main sub-structures covering the Orion A and B nebulae have been merged by our procedure in a single complex including 14 832 YSOs and a further 1 576 YSOs in the λ Ori cluster. The most distant cluster associated with Monoceros R2 (Mon-R2) is not part of the close Orion complex and includes 1272 YSOs with a mean distance of 897 pc (σ = 123 pc).
 |
Fig. C.1 YSOs associated with Taurus-Auriga selected in this work (upper panel), Krolikowski et al. (2021; middle panel), and Kerr et al. (2021; lower panel). Colours and symbols indicate the sub-structures we found with DBSCAN. those derived by the Gaussian mixture model (GMM) in Krolikowski et al. (2021), and those derived as EOM by Kerr et al. (2021). White boxes in the middle and lower panels indicate the YSOs in common with our catalogue. YSOs are overplotted on an IRIS 100 µm image (Miville-Deschênes & Lagache 2005). |
 |
Fig. C.2 Proper motions in RA and Dec, parallaxes, and CAMDs of the clusters associated with the Taurus-Auriga complex. Three representative solar metallicity isochrones from the Pisa models are also shown. Symbols and colours are as in Fig. C.1. |
 |
Fig. C.3 Spatial distribution in Galactic coordinates of YSOs associated with the Orion complex. YSOs identified in the seven substructures are drawn with different symbols and colours. |
Figure C.4 shows proper motions and parallaxes of the substructures found in the Orion area. In particular, the proper motions show a very complex kinematic pattern of the sub-clusters in this region. However, a detailed analysis of the Orion kinematics is beyond the aims of this work.
Figure C.4 also shows the CAMD of the populations associated with Orion. Even though we cannot rigorously interpret it, as our data are not corrected for reddening, we note an apparent large age spread for all the populations.
We compare our findings in the Orion complex region with the Kounkel & Covey (2019) catalogue. Details on the match between the two catalogues are given in Sect. C.4. To retrieve the YSOs identified by Kounkel & Covey (2019) in the Orion complex, we considered the 16 structures (Theia groups) from their Table 2 falling in the Orion region as defined above. 11 882 and 10 373 YSOs in the Kounkel & Covey (2019) and Kounkel et al. (2020) catalogues are associated with the Theia groups of the Orion complex, respectively. 7 983 (67%) and 7 822 (75%) are in common with the list of Orion members found in this work.
The Orion complex has been extensively investigated with Spitzer IR data. For example, the Megeath et al. (2012) catalogue includes 3 479 YSOs stars13 that cover a quite extended region of the Orion A and B nebulae. Using the cross-match service provided by CDS, Strasbourg, and a matching radius of 1″, we found that 2 612 IR sources from the Megeath et al. (2012) catalogue have a Gaia EDR3 counterpart. From this sample, we only considered those with photometric and astrometric restrictions given in Equation 1, with G-GRP > 0.58 and in the ranges of 203°< l < 216° and -30°< b < 30°, which amount to 1 667 YSOs. Of these, we identified 1 561 (~94%) as members of the Orion complex. The spatial distributions of our members and those found in Megeath et al. (2012) are shown in Fig. C.5. This high percentage proves that Gaia data can accurately confirm membership of YSOs in SFRs comparably to IR data. If we consider the sub-sample of 2612 Megeath et al. (2012) objects with Gaia counterparts, and assume that it includes only genuine YSOs (i.e. 0% contamination), we can conclude that our completeness level is about 60%. This value is the result of the restrictions we imposed on our initial data set to reduce the contamination level. We note that we can have a significant bias against (missed) binary stars. In fact, if we only discard the condition RUWE < 1.4 and retain the other conditions, there are 1953 Megeath et al. (2012) YSO Gaia counterparts, and this implies that 286 YSOs (1953–1667), that is, about 14% of the total sample (very likely binary systems), are missing from our data set. We do not attempt to estimate the fraction of false positives that could be included in our sample by considering the Megeath et al. (2012) catalogue since it mainly includes Class II stars (i.e. YSOs with IR excess emission from the circumstellar disc), and it is therefore incomplete for the Class III stars, which do not show excess emission in the IR.
 |
Fig. C.4 Proper motions in RA and Dec, parallaxes, and CAMDs of the YSOs associated with the Orion complex. The symbol colours of the sub-clusters are the same as in Fig. C.3. Three representative solar metallicity isochrones from the Pisa models are also shown. |
 |
Fig. C.5 Spatial distribution of Orion YSOs compared to YSOs found in Megeath et al. (2012), indicated as black and red symbols, respectively. YSOs in common to the two catalogues are drawn as green symbols. |
C.3 Interstellar dust-free SFR NGC2362
At a distance of 1354±192pc, NGC 2362 is an SFR characterised by a very low and uniform reddening, estimated to be E(B-V)=0.1 (Moitinho et al. 2001). For this reason, the cluster shows a small spread in the optical V versus V-I diagram, as found by Moitinho et al. (2001) and confirmed by Damiani et al. (2006). This enables us to constrain the duration of the star formation process that in this region has been about 1-2 Myr (Damiani et al. 2006). This result was derived on the basis of a Chandra-ACIS X-ray observation, pointed towards the cluster, from which a list of very likely members has been obtained. As for the case of NGC 2264, this cluster was found using our procedure in a region more extended than that investigated by Damiani et al. (2006). The 879 YSOs compatible with being members of NGC 2362 are plotted in Fig. C.6. Within the nominal cluster centre, 1=238.2°, −5.54° (Damiani et al. 2006), we found 150 candidate members, while the others are mostly concentrated around the three bumps visible in the IR image. A further sub-group of cluster members shows an aligned spatial distribution roughly going from NGC 2362 to the HII region LBN 1059.
To compare our data with the list of 387 X-ray members by Damiani et al. (2006), we cross-matched this list with the Gaia EDR3 catalogue, using the cross-match service provided by CDS, Strasbourg and adopting a matching radius of 0.5″. We find that 294 of them have a single Gaia EDR3 counterpart, but 129 are compliant with our initial data set restrictions and fall in the PMS region of the CAMD compatible with ages < 10 Myr. Among these, 118 (i.e. ~ 91%) are in common with our list of YSOs. This fraction confirms that, even though our list of YSOs is incomplete due to the significant fraction of members discarded, a priori, with the adopted data restrictions and in the adopted photometric ranges, the efficiency of our method in detecting very likely members is very high. This is notably true if we consider that X-ray detections select YSOs without any bias based on the stellar evolutionary status (Class II or III YSOs) and do so with a high degree of efficiency in the spectral types (G to M) we are working on.
Within the Chandra-ACIS field of view, we selected a total of 150 YSOs, and 32 of them (21%) are not X-ray detected. X-ray detections found in Damiani et al. (2006) are complete for masses larger than 0.4 M⊙, which, assuming the cluster age of 4-5 Myr (Mayne & Naylor 2008), corresponds to MG ≃ 7.5. By considering that more than 50% of these X-ray-undetected YSOs are fainter than this limit and that most of them are located far from the cluster centre, where the Chandra-ACIS spatial resolution is lower, we are confident that the 32 X-ray-undetected YSOs classified by us are likely members.
As for the other clusters, we investigated proper motions, parallaxes, and CAMD, which are shown in Fig. C.7. The proper motion scatter plot indicates that the distribution of YSOs falling in the Chandra-ACIS is actually more concentrated than that of the overall cluster, which shows an inclined trend. This confirms that the entire cluster is characterised by a kinematic structure slightly more complex than that of the sub-group of YSOs falling around the known cluster centre. The parallax values indicate that all the detected YSOs are located at consistent distances.
 |
Fig. C.6 Spatial distribution in Galactic coordinates of YSOs associated with NGC2362 (yellow symbols). YSOs falling in the box of 16.9″ × 16.9″ equal to the Chandra-ACIS field (white box) used in Damiani et al. (2006) are indicated as green symbols. YSOs in common with Damiani et al. (2006) X-ray detections are indicated as red symbols. Objects are overplotted on an IRIS 100 µm image. |
We note that to reduce the observed spread in the MG versus G − GRP diagram shown in Fig. C.7, in the computation of MG, we used the median cluster distance, rather than the individual member distances. The residual observed luminosity spread in the MG versus G − GRP diagram is likely due to reddening effects not corrected here and that, on the contrary, are very small in the V versus V-I diagram, where the reddening vector is almost parallel to the cluster sequence in the low-mass range (see Fig. 4 in Damiani et al. 2006).
C.4 Comparison with literature all-sky star cluster catalogues
Using the gαiαedr3.dr2neighbourhood table in the Gaia archive, we retrieved the Gaia DR2 identification number of the candidate YSOs selected in our work and thus, using these IDs, we performed the match with the Kerr et al. (2021) list, including 30518 YSOs within 333 pc and selected with Gaia DR2. We found a total of 9 351 objects in common. Among these, 4676 are associated with clusters with t ≲ 10 Myr and 3 914 are associated with clusters with 10 Myr ≲ t ≲ 100 Myr in our catalogue.
Using the same procedure as for the Kounkel & Covey (2019) and Kounkel et al. (2020) catalogues, which include 288 370 entries up to 1 Kpc and 987 376 entries up to 3 Kpc, respectively, we find a total of 38 567 and 42 350 YSOs in common. 23 071 (9 494) from the Kounkel & Covey (2019) list and 25 511 (9 559) from the Kounkel et al. (2020) list are associated with SFRs with t ≲ 10 Myr (young clusters with 10 Myr ≲ t ≲ 100 Myr). The remaining common stars have been discarded by us since they do not belong to the young age range. We note that, while in the contest of the entire all-sky catalogue the fraction o objects in common is very low (~13% and ~4%), in the region of the Orion complex it is 67% and 75% (see Sect. C.2). However, we note that our catalogue does not include the string-like massive clusters at ≳ 1 kpc with spatial distribution aligned to the GP that we discarded in the cluster-validation phase (see Sect. 4.2). Instead, the Kounkel & Covey (2019) and Kounkel et al. (2020) lists include many of these objects and this could explain the low fraction of objects in common with respect to the entire catalogue. In addition, the restrictions to the initial data set are very different. For example, we imposed a photometric selection in the extinction-uncorrected MG versus G − Grp CAMD, mainly aimed at selecting objects with ages < 10 Myr. On the contrary, in the Kounkel & Covey (2019) and Kounkel et al. (2020) catalogues, no photometric selection has been applied, and, in fact, these catalogues include up to ~ 1-Gyr-old clusters.
We also compared our results with the list of 2017 clusters recently published by Cantat-Gaudin & Anders (2020) that includes 234 128 cluster members. They used the most complete list of clusters from the literature and assigned them cluster membership using the UPMASK procedure (Krone-Martins & Moitinho 2014), which is based on the compactness of the groups in the positional space and is constrained to a fixed field of view. Reliable parameters have been derived for 1 867 of these clusters.
We find that 12 438 members presented by Cantat-Gaudin & Anders (2020) are in common with our catalogue. Those associated with SFRs (t ≲ 10 Myr) and young (10 Myr ≲ t ≲ 100 Myr) and old (t ≳ 100 Myr) clusters are 6 788, 2 519, and 2 109, respectively, corresponding to 66, 38, and 76 clusters in our catalogue, in the same age ranges. They belong to 311 clusters of the Cantat-Gaudin & Anders (2020) list14 with parallaxes > 0.617 mas, which approximatively corresponds to the maximum distance of YSOs identified in our work. In the Cantat-Gaudin & Anders (2020) catalogue, there is a total of 49074 cluster members with π > 0.617, G > 7.5, and MG > 5.0, and therefore we find that only ~ 25% of YSOs detected by us are in common with Cantat-Gaudin & Anders (2020). Using the ages derived in Cantat-Gaudin & Anders (2020), we find that 226 of the matched clusters are older than 10 Myr.
For the 331 clusters in common, we compared the distances assigned by Cantat-Gaudin & Anders (2020) computed as the inverted parallaxes of the value given for each cluster and the mean distance obtained by us, which was computed from the weighted mean parallaxes. Errors on the parallaxes were computed as the error on the mean. The comparison is shown in Fig. C.8, where the mean and standard deviation of the residuals between the two measurement sets are also given. The two determinations are consistent, even though there is a bias due to the different Gaia data releases adopted in our work (EDR3) and in Cantat-Gaudin & Anders (2020; DR2).
 |
Fig. C.7 Proper motions in RA and Dec, parallaxes, and CAMDs of the YSOs associated with NGC 2362. Symbol colours are as in Fig. C.6. Black x symbols are the X-ray-detected YSOs by Damiani et al. (2006). Four representative solar metallicity isochrones from the Pisa models are also shown. |
 |
Fig. C.8 Comparison between cluster distances derived by Cantat-Gaudin & Anders (2020) and those derived in this work. The line with slope one is shown for guidance. |
References
- Alves, J., Zucker, C., Goodman, A. A., et al. 2020, Nature, 578, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, F., Khalatyan, A., Chiappini, C., et al. 2019, A&A, 628, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avedisova, V. S. 2002, Astron. Rep., 46, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bica, E., Pavani, D. B., Bonatto, C. J., & Lima, E. F. 2019, AJ, 157, 12 [Google Scholar]
- Bonito, R., Prisinzano, L., Guarcello, M. G., & Micela, G. 2013, A&A, 556, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouy, H., & Alves, J. 2015, A&A, 584, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J., Rix, H.-W., Green, G. M., Schlafly, E. F., & Finkbeiner, D. P. 2016, ApJ, 818, 130 [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., & Anders, F. 2020, A&A, 633, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Anders, F., Castro-Ginard, A., et al. 2020, A&A, 640, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Ginard, A., Jordi, C., Luri, X., et al. 2018, A&A, 618, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Ginard, A., Jordi, C., Luri, X., et al. 2020, A&A, 635, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chen, W. P., & Lee, H. T. 2008, in Handbook of Star Forming Regions, ed. B. Reipurth, 4, 124 [NASA ADS] [Google Scholar]
- Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [Google Scholar]
- Cody, A. M., Stauffer, J., Baglin, A., et al. 2014, AJ, 147, 82 [Google Scholar]
- Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in SPIE Conf. Ser., 8446, 84460P [Google Scholar]
- Damiani, F., Micela, G., Sciortino, S., et al. 2006, A&A, 460, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, F., Prisinzano, L., Pillitteri, I., Micela, G., & Sciortino, S. 2019, A&A, 623, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Prada Moroni, P.G. 2012, A&A, 540, A26 [CrossRef] [EDP Sciences] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutra, C. M., & Bica, E. 2002, A&A, 383, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., Picogna, G., Monsch, K., Drake, J. J., & Preibisch, T. 2021, MNRAS, 508, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. 1996, in Second International Conference on Knowledge Discovery and Data Mining, eds. J. Simoudis, E. Han, & U. Fayyad (Menlo Park, CA: AAAI Press), 226 [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D. 2018, in Astrophysics and Space Science Library, The Birth of Star Clusters, ed. S. Stahler, 424, 119 [NASA ADS] [Google Scholar]
- Fernández-López, M., Arce, H. G., Looney, L., et al. 2014, ApJ, 790, L19 [Google Scholar]
- Flaccomio, E., Micela, G., & Sciortino, S. 2006, A&A, 455, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franciosini, E., Tognelli, E., Degl’Innocenti, S., et al. 2021, A&A, 659, A85 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gould, B. A. 1879, Result. Observ. Nacional Argentino, 1, 1 [Google Scholar]
- Guiglion, G., Battistini, C., Bell, C. P. M., et al. 2019, The Messenger, 175, 17 [NASA ADS] [Google Scholar]
- Guillout, P. 2001, in Astronomical Society of the Pacific Conference Series, From Darkness to Light: Origin and Evolution of Young Stellar Clusters, eds. T. Montmerle, & P. André, 243, 677 [Google Scholar]
- Gullbring, E., Hartmann, L., Briceno, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, R. J., Jeffries, R. D., Wright, N. J., et al. 2022, MNRAS, 509, 1664 [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Franciosini, E., et al. 2017, MNRAS, 464, 1456 [Google Scholar]
- Kerr, R. M. P., Rizzuto, A. C., Kraus, A. L., & Offner, S. S. R. 2021, ApJ, 917, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kounkel, M., & Covey, K. 2019, AJ, 158, 122 [Google Scholar]
- Kounkel, M., Covey, K., & Stassun, K. G. 2020, AJ, 160, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Hillenbrand, L. A., & Martinache, F. 2012, ApJ, 745, 19 [Google Scholar]
- Krolikowski, D. M., Kraus, A. L., & Rizzuto, A. C. 2021, AJ, 162, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberger, M., Teutsch, P., Alessi, B., et al. 2006, A&A, 447, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krone-Martins, A., & Moitinho, A. 2014, A&A, 561, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J. 2006, ApJ, 640, L63 [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Duigou, J. M., & Knödlseder, J. 2002, A&A, 392, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021a, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021b, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Liu, L., & Pang, X. 2019, ApJS, 245, 32 [CrossRef] [Google Scholar]
- Luhman, K. L. 2022, AJ, 163, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D. 1994, ARA&A, 32, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- McInnes, L., Healy, J., & Astels, S. 2017, JOSS, 2, 205 [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2012, AJ, 144, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra-Kraev, U., Harra, L. K., Güdel, M., et al. 2005, A&A, 431, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [Google Scholar]
- Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57 [Google Scholar]
- Moitinho, A., Alves, J., Huélamo, N., & Lada, C. J. 2001, ApJ, 563, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalto, M., Piotto, G., Marrese, P. M., et al. 2021, A&A, 653, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otrupcek, R. E., Hartley, M., & Wang, J. S. 2000, PASA, 17, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., Randich, S., Flaccomio, E., & Pallavicini, R. 2005, ApJ, 626, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1983, MNRAS, 202, 615 [NASA ADS] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Piecka, M., & Paunzen, E. 2021, BAJ, accepted [arXiv:2107.07230] [Google Scholar]
- Poggio, E., Drimmel, R., Cantat-Gaudin, T., et al. 2021, A&A, 651, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prisinzano, L., Damiani, F., Micela, G., & Sciortino, S. 2005, A&A, 430, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Randich, S., Tognelli, E., Jackson, R., et al. 2018, A&A, 612, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Johnson, C. H., Gibbs, J. C., et al. 2013, AJ, 145, 15 [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scalo, J. 1998, in ASP Conf. Ser. 142: The Stellar Initial Mass Function (38th Herstmonceux Conference), 201 [Google Scholar]
- Sitnik, T. G. 2003, Astron. Lett., 29, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Hillenbrand, L. A., Jeffries, R. D., Mamajek, E. E., & Naylor, T. 2014, Protostars and Planets VI, 219 [Google Scholar]
- Somers, G., Cao, L., & Pinsonneault, M. H. 2020, ApJ, 891, 29 [Google Scholar]
- Spina, L., Randich, S., Magrini, L., et al. 2017, A&A, 601, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2018, MNRAS, 476, 27 [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., Degl’Innocenti, S., Salaris, M., & Cassisi, S. 2020, A&A, 638, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Damiani, F., & Prisinzano, L. 2019, A&A, 621, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yonekura, Y., Dobashi, K., Mizuno, A., Ogawa, H., & Fukui, Y. 1997, ApJS, 110, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Zari, E., Hashemi, H., Brown, A. G. A., Jardine, K., & de Zeeuw, P. T. 2018, A&A, 620, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, Res. Astron. Astrophys., 12, 723 [CrossRef] [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2020, A&A, 633, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
See https://www.cosmos.esa.int/web/gaia/edr3-passbands for further details
Available at https://github.com/syrte/ndtest
Using the Gaia DR2 number, we cross-matched the Kerr et al. (2021) and Damiani et al. (2019) lists and found 6423 objects in common.
For a direct visual comparison, spatial limits of the figure are the same as those used in Fig. 1 of Kounkel & Covey (2019).
This apparent discrepancy is due to the fact that our catalogue includes merged clusters that can include more than one cluster in the Cantat-Gaudin & Anders (2020) list.
All Tables
All Figures
 |
Fig. 1 CAMD of YSOs of some representative young clusters with membership probabilities >0.90 assigned by combining spectroscopic and Gaia EDR3 criteria (Jackson et al. 2022). Blue x symbols trace the empirical sequence by Pecaut & Mamajek (2013). Members of the clusters Gamma Velorum (18 Myr old) and NGC2451b (50 Myr old) are also shown. Black solid lines are the theoretical solar metallicity Pisa isochrones while the red solid line is the complete photometric limit adopted in this work including the low mass extrapolation. Dashed, dashed-dotted and dotted lines are the 10 Myr isochrones at different metallicities. Blue and green solid lines represent the limits described by the equations 2 and 3. |
| In the text | |
 |
Fig. 2 CAMD of YSOs identified in clusters with ages t ≲ 10 Myr included in the template data set. Black solid lines are the theoretical solar metallicity Pisa isochrones of 1, 10, and 100 Myr isochrones (from right to left). The number on the top right edge of each panel is the flag assigned to each cluster. |
| In the text | |
 |
Fig. 3 CAMD of clusters with ages 10 Myr ≲ t ≲ 100 Myr, flagged from 29 to 36, and with ages t ≳ 100 Myr, flagged from 37 to 52, included in the template data set. Black solid lines are as in Fig. 2. The number on the top right edge of each panel is the flag assigned to the clusters. |
| In the text | |
 |
Fig. 4 Density map of three orientations of the GP of YSOs associated with SFRs with ages of t ≲ 10 Myr. In the upper left panel, the Sun is at (0, 0), the x-axis is directed towards the Galactic centre, and the y-axis is towards the direction of the Galactic rotation. Dashed white circles are drawn at distance steps of 500 pc. In the upper right and lower left panels, the z-axis is perpendicular to the GP. Colour bars indicate the surface densities, that is, the number of stars per bin and per pc2. Some known SFRs are indicated. The numbers from 1 to 9 in the upper right and bottom panels indicate the position of the clusters indicated in Fig. 5 (upper left panel). |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for stars associated with clusters of ages 10 Myr ≲ t ≲ 100 Myr. |
| In the text | |
 |
Fig. 6 Spatial distributions in Galactic coordinates of YSOs associated with the Sco-OB2 Association. The de Zeeuw et al. (1999) sub-regions of US, UCL, LCC are shown. The different colours indicate all the different substructures found in this region. |
| In the text | |
 |
Fig. 7 Proper motions in RA and Dec, parallaxes, and CAMDs of the groups of YSOs associated with the Sco OB2 association. The symbol colours are as in Fig. 6. Three representative solar metallicity isochrones from the Pisa models are also shown as solid lines in the right panels. |
| In the text | |
 |
Fig. 8 Spatial distribution in equatorial coordinates of the YSOs associated with NGC 2264, NGC 2244, Mon R2, CMA OB1, and UPK436. YSOs are overplotted on an IRIS 100 µm image (Miville-Deschênes & Lagache 2005). For clarity, Orion members have not been plotted. |
| In the text | |
 |
Fig. 9 Proper motions in RA and Dec, parallaxes, and CAMDs of the SFRs falling in the field of view of NGC 2264. The symbol colours of the clusters are as in Fig. 8. Three representative solar metallicity isochrones computed from the Pisa models are also shown. |
| In the text | |
 |
Fig. 10 Aitoff projections in Galactic coordinates of the YSOs in the different age bins (t < 10 Myr, 10 Myr < t < 100 Myr and t ≲ 100 Myr), with distance in the range ([100, 600] pc (left panels), [600, 2000] pc (mid right panel) and [100, 2000] pc) (upper and bottom right panels). Colour codes indicate stellar distances. |
| In the text | |
 |
Fig. A.1 PARSEC 1 Gyr isochrone at solar metallicity with extinction, AV, ranging from 0 to 10.0 in the CAMD obtained by adopting the different Gaia magnitudes (black dots). The 1 Gyr isochrone at AV = 0 is highlighted by a thick black solid line. The 1 Gyr isochrone at AV = 3 is highlighted by pink coloured lines of different shades during the red giant branch (RGB), asymptotic giant branch (AGB), red clump (RC), sub-giant (subGig), and MS phases. The red, light-blue, and green solid lines are the 1, 10, and 50 Myr Pisa isochrones at solar metallicity. The empty square and the bullet in each panel represent a star of 6930 K and 3945 K, respectively, while the blue and red arrows are the reddening vectors corresponding to AV = 3, for these two representative stars (see text). |
| In the text | |
 |
Fig. B.1 Diagram of RUWE values versus the Gaia colour GBP–GRP of the Kraus et al. (2012) Taurus-Auriga binary-star list with Gaia EDR3 counterparts. Filled symbols are the binaries also selected in this work, while empty symbols are those rejected. |
| In the text | |
 |
Fig. B.2 Diagram of RUWE values versus the binary separation of the Kraus et al. (2012) Taurus-Auriga binary-star list with Gaia EDR3 counterparts. Symbols are as in Fig. B.l. |
| In the text | |
 |
Fig. C.1 YSOs associated with Taurus-Auriga selected in this work (upper panel), Krolikowski et al. (2021; middle panel), and Kerr et al. (2021; lower panel). Colours and symbols indicate the sub-structures we found with DBSCAN. those derived by the Gaussian mixture model (GMM) in Krolikowski et al. (2021), and those derived as EOM by Kerr et al. (2021). White boxes in the middle and lower panels indicate the YSOs in common with our catalogue. YSOs are overplotted on an IRIS 100 µm image (Miville-Deschênes & Lagache 2005). |
| In the text | |
 |
Fig. C.2 Proper motions in RA and Dec, parallaxes, and CAMDs of the clusters associated with the Taurus-Auriga complex. Three representative solar metallicity isochrones from the Pisa models are also shown. Symbols and colours are as in Fig. C.1. |
| In the text | |
 |
Fig. C.3 Spatial distribution in Galactic coordinates of YSOs associated with the Orion complex. YSOs identified in the seven substructures are drawn with different symbols and colours. |
| In the text | |
 |
Fig. C.4 Proper motions in RA and Dec, parallaxes, and CAMDs of the YSOs associated with the Orion complex. The symbol colours of the sub-clusters are the same as in Fig. C.3. Three representative solar metallicity isochrones from the Pisa models are also shown. |
| In the text | |
 |
Fig. C.5 Spatial distribution of Orion YSOs compared to YSOs found in Megeath et al. (2012), indicated as black and red symbols, respectively. YSOs in common to the two catalogues are drawn as green symbols. |
| In the text | |
 |
Fig. C.6 Spatial distribution in Galactic coordinates of YSOs associated with NGC2362 (yellow symbols). YSOs falling in the box of 16.9″ × 16.9″ equal to the Chandra-ACIS field (white box) used in Damiani et al. (2006) are indicated as green symbols. YSOs in common with Damiani et al. (2006) X-ray detections are indicated as red symbols. Objects are overplotted on an IRIS 100 µm image. |
| In the text | |
 |
Fig. C.7 Proper motions in RA and Dec, parallaxes, and CAMDs of the YSOs associated with NGC 2362. Symbol colours are as in Fig. C.6. Black x symbols are the X-ray-detected YSOs by Damiani et al. (2006). Four representative solar metallicity isochrones from the Pisa models are also shown. |
| In the text | |
 |
Fig. C.8 Comparison between cluster distances derived by Cantat-Gaudin & Anders (2020) and those derived in this work. The line with slope one is shown for guidance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


