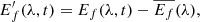© M. J. Korpi-Lagg et al. 2022

1. Introduction

Localized regions of intense bipolar magnetic structures, known as active regions (ARs), are seen on the solar surface. Their numbers vary periodically in an 11-year cycle and trace the butterfly diagram, which reveals a cyclic magnetic activity of the Sun in a latitude–time domain. Such diagrams have proven to be useful and reveal some properties of the solar large-scale magnetic field. The large-scale magnetic field reverses its polarity every second such cycle, which constitutes the solar magnetic cycle of 22 years. The origin of this global variability is not yet fully understood (see, e.g., Charbonneau 2010).

In addition to the global solar magnetic field, it is observationally known that there are ubiquitous small-scale magnetic fluctuations, the origin of which is equally debated – they could arise through the action of a small-scale dynamo instability or tangling of the large-scale magnetic field due to turbulence driven by convection, but it is not self-evident how the former mechanism could work in the solar plasma, where the conditions are in general unfavourable for it (see, e.g., Brandenburg & Subramanian 2005). These magnetic fluctuations are usually studied by investigating the magnetically quiet regions on the solar surface (hereafter referred to as the quiet Sun, QS). Several observational studies of QS magnetism have been conducted and it has been argued that the QS magnetic field is independent of the solar cycle (see, e.g., Kleint et al. 2010; Buehler et al. 2013; Faurobert & Ricort 2015; Jin & Wang 2015a, 2015b). On the other hand, some other studies have proposed that some dependence should exist (e.g., Lites et al. 2014; Meunier 2018; Faurobert & Ricort 2021). Given the theoretical and observational controversies, further studies of QS magnetism are required and long-term investigations are now enabled by instruments like Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012; Schou et al. 2012) on board the Solar Dynamics Observatory (SDO, Pesnell et al. 2012) This instrument provides high sensitivity, high spatial resolution, long-term stability, and constant conditions. Currently, the data covers 12 years of observations, enabling solar-cycle-scale studies.

Another motivation to study the QS comes from recent observational investigations (Singh et al. 2016; Waidele et al. 2022) that have reported a strengthening of the solar surface or the fundamental f-mode about one to two days before the formation of ARs using different kinds of local helioseismic techniques. Accompanied with numerical simulations that have given similar indications Singh et al. (2014, 2015, 2020), this appears a very promising avenue for studying the origin of solar sub-surface magnetism and the mechanism of active region formation. The observational studies, however, suffer from a lack of proper calibration method against the QS. Singh et al. (2016), for example, rely on QS regions on the opposite hemisphere to compare with the AR f-modens. This method requires that a quiet patch exists on the other hemisphere, and hence limits the number of ARs that can be included in the hindcasting procedure. It is also prone to be affected by the probable fluctuations in the QS f-mode level. Although the results look promising, a proper calibration with a statistically sound QS level (not just a comparison of a random QS patch on the other hemisphere) is necessary to prove the robustness of these findings. Also, such a calibration procedure is required for increasing the sample size. Building such a QS calibration data product is one of the main aims of this study: we carefully identified the quietest regions on the solar surface based on the level of magnetic activity observed in line-of-sight (LOS) magnetograms that are readily available from HMI and computed the f-mode energy at the central meridian as function of latitude and time with suitable averaging. Building such a data product for the f-mode, requiring us to identify the most inactive regions on the solar surface, allowed us to extract statistics of the QS magnetism as well, which is the second main aim of this study.

The paper is organized as follows. In Sect. 2 we describe the data, the necessary steps to clean it, and the automated pipeline we built for harvesting the data and compiling the end products; namely, the QS magnetism data products, as well as the QS and AR f-mode data. In Sect. 3, we discuss our findings for the QS magnetism and f-mode, and lastly, we present a set of the AR data with the QS calibration applied.

2. Observations

Our analysis is based on data from HMI at SDO. We used two standard data products: (i) full-disk line-of-sight (LOS) magnetograms, computed every 720 s by combining filtergrams obtained over a time interval of 1260 s (hmi.M_720s) and (ii) full-disk LOS dopplergrams, computed every 45 s from six positions across the nominal 6173.3 Å spectral line (hmi.V_45s). We processed the two data sets in a semi-automatic pipeline (see Fig. 1), optimized for obtaining reliable information about the magnetic field in the QS regions and for a robust computation of the f-mode power from the dopplergrams. The left tree in Fig. 1 describes the pipeline used for the magnetograms, the right tree for the dopplergrams. We use the following notations and definitions: we denote the solar latitude with λ, longitude with φ, both in the Stonyhurst coordinate system (Thompson 2006), and time with t.

Fig. 1. Data pipeline deployed in the CSC HPC environment. The leftmost tree illustrates the pipeline to collect the magnetograms in the most quiet patches, while the rightmost one the pipeline to track data from the quiet patches from the HMI database, and compute the f-mode energy. The central path of AR processing is otherwise equivalent to the QS pipeline, but their AR coordinates are sent for tracking in the MPS (in Germany) cluster environment, followed by an additional step, namely, QS calibration, at the end. Rectangular boxes represent analysis functions and ellipsoids are the derived data products. The rectangles with yellow frames stand for the corrective functions applied to the data.

2.1. Magnetograms

The first data product, namely, the full-disk line-of-sight (LOS) magnetograms, provides a direct measurement of the variability of the QS magnetism during a solar cycle. To enhance the signal-to-noise ratio (S/N) in the LOS magnetograms we performed a newly developed algorithm for spatial and temporal averaging: The full-disk HMI magnetograms starting from 27-Apr.-2010 and ending on 04-May-2022 were downloaded from the Joint Science Operation Center (JSOC) hosted at Stanford University¹ to a temporary storage (see Fig. 1, ‘Mahti storage’) and tracked at full spatial resolution for 8 h to compensate for the solar rotation (‘Full disk tracking’). We neglected differential rotation due to the short tracking time. The step between tracked sequences was 4 h, so that a total of 6 tracked sequences were gathered per one day, resulting in more than 25 700 tracked sequences (as of 04-May-2022).

From each tracked sequence, we extracted two data products by dividing the visible solar disk between latitudes and longitudes from −80° to +80° into (i) 64 × 64 overlapping patches of 15° (in solar latitude and longitude) and (ii) 180 × 180 patches of 1°. Every of these patches therefore contains a space-time cube of LOS magnetograms at full spatial resolution at a 12-min cadence, from which we computed the root-mean-square (rms) of the magnetic field strength, averaged over the full field of view (FoV) of the tracked cube and over the full 8 h period ($B_{\mathrm{rms}}=\sqrt{{⟨B^2⟩}_{\mathrm{LOS}}}$). The 15° patches (i) are large enough to cover several supergranulation cells containing network and internetwork fields (Rieutord & Rincon 2010) with a typical size of 30–35 Mm (we refer to them as Nw cubes), and the 1° patches (ii) are small enough that some of them lie completely in the internetwork (INw cubes). The statistics for each patch were stored as data products (see also Fig. 1) including the information about latitudinal and longitudinal position as well as the Carrington longitude for network and internetwork. We refer to these maps as the Nw and the INw statistical maps.

2.2. Quiet region selection

From the statistics computed from the cubes, B_rms turned out to be the best tracer for determining the magnetic activity level. It could clearly distinguish between 15° patches containing active regions, plage, enhanced network and quiet network. Also, it depicted the low-field internetwork regions very well.

The analysis of the solar-cycle variation of the QS magnetism requires a careful selection of the most quiet regions, defined as being free of enhanced solar activity. We therefore searched for the minimum value of B_rms in both, the Nw and the INw statistical maps, on a latitudinal grid with a 10° spacing fulfilling the following additional criteria: (i) the most quiet pixel must be within ±10° around the central meridian, (ii) this pixel must belong to the 10% most quiet pixels of the month, and (iii) this pixel must be the most quiet pixel within a 4-day interval.

Criterion (i) was chosen because the central meridian offers the highest sensitivity for magnetic field measurements, criterion (ii) guarantees an equal distribution of quiet pixels over the 12-year period of available HMI measurements; and criterion (iii) ensures that the quiet pixels for the 1-month period do not originate from the same supergranular structure, since the dynamical evolution time of the supergranulation lies between 24 and 48 h (Rieutord & Rincon 2010). As a result of applying these criteria we obtained two time series of the B_rms for the most quiet patches in the network and the internetwork regions. We note that this selection also efficiently removes the 24 h modulation present in the HMI magnetograms.

2.3. Correction for HMI sensitivity change

The temporal evolution of INwB_rms value clearly revealed a change in the HMI observing mode, performed on 13-Apr.-2016. On this day, HMI switched to a more efficient observing mode (see Hoeksema et al. 2018, 2014; Couvidat et al. 2016). By combining both HMI cameras to determine the vector-field observables the cadence for full-disk magnetograms could be reduced from 135 s (observational mode MOD-C) to 90 s (MOD-L). This reduced the noise level for Stokes V measurements by 17%, resulting in a decrease of the noise level in the LOS magnetograms by 5%.

For the long-term study presented in this paper, we need to correct for this sensitivity change. A very accurate correction method can be derived from the INw time series: since it contains only the most quiet pixels over a certain latitude region and time, the sensitivity change results in a step function. The value of the step was determined by fitting a polynomial to the B_rms values determined from the INw time series plus a Heaviside step function, centered at the date of the mode change. We used the Bayesian information criterion (BIC, Stoica & Selen 2004) to determine the degree of the polynomial, which lies between 1 and 6 for the various latitudes. We want to note that the retrieved amplitude of the Heaviside step function is only weakly dependent on the degree of the polynomial. This fitting is exemplified in Fig. 2 for the solar latitude 0°, where the minimum value for the BIC was reached for a fit with a polynomial of degree of 3. The thus-determined amplitude of the Heaviside step function is added to the B_rms data points after 13-Apr.-2016 for all data presented in this paper. No other correction, such as de-trending, was applied to the data.

Fig. 2. Determination of the correction for the HMI sensitivity change: observing mode change on 13 Apr. 2016 causes a discontinuity in the level of Brms values of the internetwork data. The original data are displayed with the dark red and black dots, the corrected data with the light red dots. The dashed line indicates the polynomial fit of a degree of 3 used to obtain the offset.

2.4. Dopplergrams

The second HMI data product used in this paper is the LOS velocity maps. The goal is to compute the energy contained in the surface gravity mode, the so-called f-mode, and investigate whether variability during the solar cycle is present. Such variations could be caused by the presence of non-emerging sub-surface magnetic fields, as the f-mode is known to be strongly affected by the presence of magnetic fields (see, e.g., Cally et al. 1994; Cally & Bogdan 1997; Singh et al. 2016). It is also very important to study this question in more detail for the purpose of establishing a reliable calibration method for a measurement of the claimed f-mode enhancement prior to AR emergence Singh et al. (2016), Waidele et al. (2022).

The dopplergram data is hosted in the German Data Center for SDO (GDC-SDO) on a server at the Max Planck Institute for Solar System Research (MPS Göttingen, Germany), whereas the analysis is executed in the CSC supercomputing environment (Finland). We utilized a function-as-a-service client based on funcX (Chard et al. 2020) for accessing the required data in the database server. We developed functions based on funcX API and deployed the functions in the MPS environment. These functions leverage the mtrack² command to prepare the dopplergram cubes within the GDC-SDO environment and subsequently transfer them to the CSC environment. The coordinates of the selected QS regions were sent to the funcX service, which invokes suitable functions to automate the data retrieval and movement. The data processing pipeline used Astropy³, a community-developed core Python package for astronomy (Astropy Collaboration 2013, 2018) and version 3.1.6 of the SunPy⁴ open source software package (The SunPy Community 2020).

2.5. Computation of the f-mode energy

Subsequent processing involved calculating the three-dimensional power spectra for each dopplergram cube and integrating in the (k_x, k_y)-plane, for each angular frequency ω, over all wavenumbers, $k=\sqrt{k_x^2+k_y^2}$, to obtain a collapsed power spectrum, P(ω, k). An illustrative case for a frequency, ν = ω/2π, at which the f-mode is strong, is shown in Fig. 3 (upper panel). Such a procedure significantly reduced the noise level, leading to smooth one-dimensional (1D) k − ω spectra (as, e.g., shown in the lower panel of Fig. 3; in this kind of a plot, the f-mode is the rightmost peak at the highest k values). The adopted procedure is justified for the QS spectra, as the ring diagrams are radially symmetrical with regard to the frequency axis. To obtain the total energy contained in the f-mode, E_f, we performed another integration over the separated f-mode signal. In contrast to earlier studies (Singh et al. 2016; Waidele et al. 2022), we did not perform fitting to the f-mode for its extraction. Instead, we only determined the background signal, and subtracted this contribution. The background determination made use of the fact that the position of the f-mode peak for low values for the frequency (ν between 1.0 and 2.0 mHz) lies outside the k range used for the computation of the f-mode power. Since the background level does not change significantly with the frequency, the average spectrum over this range provided a good estimate for the background signal. Then, an integration range in k space was selected for each constant frequency in a following way: first the maximum of f-mode k_max and the minimum between f-mode and first p-mode k_start were detected; k_start was chosen as the start of integration range and the end of the integration range k_end was set as k_end = k_max + 2(k_max − k_start); k_end chosen in such a way guarantees that the integration range is sufficiently wide to cover significant part of the f-mode signal in the k-space. The integration range in the frequency space was chosen between ν values starting from 2.3 mHz and ending at 4.6 mHz, where the significant part of the f-mode power resides. As the end result, we computed the f-mode energy:

$$\begin{array}{c}\hfill E_f={\displaystyle \sum _{k_{\mathrm{start}}}^{k_{\mathrm{end}}}\sum _{{\nu }_{\min }}^{{\nu }_{\max }}}P(\nu ,k).\end{array}$$(1)

Fig. 3. Examples of a typical QS f-mode spectra. Top: example of QS ring diagram at the angular frequency ν = 3.57 mHz for one quadrant of the full ring (logarithmic color scale), computed from the data cube presented in Fig. 4 (left panel). Bottom: collapsed spectrum obtained by integrating over the ring diagram. The red vertical line marks the position of the maximum of the f-mode and the black vertical lines the range of integration. The wavenumber k is expressed in units of the circumference of the Sun (CSun).

After completing the described steps in the CSC supercomputing environment, we collected a total of 22 680 f-mode energies for patches close to central meridian over all latitudes, covering most of SC24 and the ascending phase of SC25.

Fig. 4. Comparison of two disk-center magnetograms at solar minimum (21 Jul. 2010) and around the maximum seen in the disk-center Brms values (09 Nov. 2014). The maps show the first frame of the 8 h data cube.

2.5.1. Orbital correction of the f-mode energy

Since the f-mode energy is computed from the LOS dopplergrams, its value depends strongly on the viewing geometry. This dependence, roughly following the cosine of the solar latitude for data taken at the central meridian, is additionally modulated by the orbital motion of the Earth around the Sun, which changes the viewing angle at any given solar latitude by ≈ ±  7° during a single year. We compensated for this periodic variation by fitting the parameters (x₀(λ),…,x₃(λ)) of the following function to all observations of a given latitude λ:

$$\begin{array}{cc}\hfill A_{\text{corr}}(\lambda )& =x_0(\lambda )(2{((1+cos(\mathrm{\Phi }+x_1(\lambda )))/2)}^{x_3(\lambda )}-1)\hfill \\ \hfill & +x_2(\lambda ),\hfill \end{array}$$(2)

with Φ being the phase angle of the Earth defined as the cotangens computed from the x, y barycentric position of the Earth. This correction A_corr(λ) is then subtracted from the computed E_f values, which efficiently removes any yearly variation.

3. Results

After applying the selection criteria described in Sect. 2.2 and the subsequent correction for the HMI’s sensitivity change (Sect. 2.3) we obtain the dependency of the B_rms values of the most quiet region at the central longitude as a function of heliographic latitude and time. In Fig. 5, we present the B_rms values from May 2010 until May 2022 for the Stonyhurst latitude and longitude (λ, φ)=(0, 0)°. The individual data points (red dots) are computed over an area of 15° in latitude and longitude and over a period of 8 hours. At disk center, this corresponds to an area of ≈180 × 180 Mm², and therefore contains 30–40 supergranular cells. The B_rms value thus contains network and internetwork fields. Typical magnetograms at disk center at solar minimum (July 2010) and maximum (Nov. 2014) are presented in Fig. 4. There is no obvious difference between the two maps: both show similar minimum and maximum field strengths, and the visible impression of the supergranular cells with the strong field patches of both polarities surrounding the internetwork regions is indistinguishable.

Fig. 5. Brms determined from the most quiet patches from 2010 to 2022 at disk center. The patches of 15° size in longitude and latitude contain network and internetwork fields. The solid red lines display the 97% percentile level, the dashed gray line the mode of a log-normal fit to yearly-binned data moved in a sliding window of 100 days length. For all values of ω, the magnitude of P is always an order of magnitude higher than the noise level outside the considered location of the ring.

In Fig. 5, we can clearly see the solar cycle dependence of the QS magnetic fields, consisting of network and internetwork. The B_rms values peak in the second half of 2014, around half a year later compared to the declared maximum of solar cycle #24 (April 2014, source: WDC-SILSO, Royal Observatory of Belgium, Brussels). The variation is statistically significant, as indicated by the mode and the 97% percentiles, computed by fitting a log-normal distribution over a 1-year sliding window.

A similar plot is presented in Fig. 6, but now the B_rms value was computed only for a 1° window in latitude and longitude, corresponding to an area of only 12 × 12 Mm² at disk center. The quiet-region selection criteria (Sect. 2.2) guarantees that this patch lies fully within the internetwork and is not “contaminated” by network fields. Clearly, there is no detectable dependence of B_rms on the solar cycle. The slight increase over the 12-year period might be an effect of the aging of the HMI instrument and the resulting decrease in the sensitivity for magnetic field measurements.

Fig. 6. Brms determined from the most quiet patches from 2010 to 2022 at disk center, but in contrast to Fig. 5, the patch size was 1° in longitude and latitude, corresponding to internetwork patches. The color and labeling scheme is the same as in Fig. 5. For all values of ω, the magnitude of P is always an order of magnitude higher than the noise level outside the considered location of the ring.

The average B_rms value in the internetwork is in ≈6 G. Using the area of one HMI pixel, this corresponds to a magnetic flux of 3 × 10¹⁶ Mx. This value is certainly affected by the sensitivity of the HMI instrument, and is reduced to ≲5 G after the HMI sensitivity change described in Sect. 2.3.

3.1. Quiet-Sun f-mode butterfly diagram

To investigate whether the f-mode energy has any significant solar cycle dependence, we constructed butterfly-diagram-like plots by computing and removing the temporal mean, and then plotting the so-obtained data in a binned latitude–time diagram. We compute the temporal mean over the whole time series as

$$\begin{array}{c}\hfill \overline{E_f}(\lambda )=1/n_{\mathrm{t}}{\displaystyle \sum _t}{E}_f(\lambda ,t),\end{array}$$(3)

where n_t is the total number of time points at a certain λ, denoted with an overbar. Next, we compute the variation of the f-mode energy around this level, defined as

$$\begin{array}{c}\hfill E_f^{\prime }(\lambda ,t)=E_f(\lambda ,t)-\overline{E_f}(\lambda ),\end{array}$$(4)

and plot this quantity for the central meridian as function of latitude and time as in Fig. 7, in patches with a 3-month binning in time and roughly 6 degrees in latitude.

Fig. 7. Butterfly diagram of f-mode energy variations, $E_f^{\prime }(\lambda ,t)$, computed from the collapsed ring diagrams (see bottom panel of Fig. 3). The temporal average, $\overline{E_f}(\lambda )$, has been subtracted from the data, and is shown as the black line in the right panel. Its error bars represent the time-averaged standard deviation of the fluctuations of the f-mode energy around the signal for every bin ($\overline{\sigma }(\lambda )$).

To estimate the overall variability level of the QS, and compare it to the cycle variation level defined above, we use the standard deviation of the data in a patch. We take N_t bins in time, N_λ in latitude, and denote the number of E_f measurements contained in such a patch by N_P. We compute the average f-mode energy in a patch as:

$$\begin{array}{c}\hfill ⟨E_f⟩=1/N_{\mathrm{P}}{\displaystyle \sum _{N_{\mathrm{P}}}}{E}_f(\lambda ,t).\end{array}$$(5)

Then we can straightforwardly calculate the standard deviation as:

$$\begin{array}{c}\hfill \sigma =\sqrt{\frac{1}{N_{\mathrm{P}}}{\displaystyle \sum _{\text{patch}}}{(E_f(\lambda ,t)-\langle E_f\rangle )}^2}.\end{array}$$(6)

On this basis, we form the average error at each latitude by taking an average over time and denote it as $\overline{\sigma }$. This quantity is plotted as the error bar in the right panel of Fig. 7. By inspecting the level of variability around the temporal mean and the overall variability of the QS, we must conclude that these signals are of the same order of magnitude. In this respect, the solar cycle dependent signal is very weak, but if we compare that to the noise level in the data, both the QS variability level and cycle-dependent signal exceed the noise level by an order of magnitude; hence, this is not an issue related to the instrument sensitivity. We also note that the time evolution of the f-mode in the northern hemisphere between the third and fourth quarter of the year 2018 appears very abrupt, as if some instrumental change in sensitivity would have taken place. We did search for such factors and found a focus update in the HMI instrument on 16 Oct. 2018, but correcting for this effect introduced a similar jump in the southern hemisphere. Hence, it is difficult to attribute the jump to this particular change, taken that some other focus adjustments happened at other times, with no significant jumps in the f-mode.

The potential cause of the strong QS variability level is most likely related to the strongly varying sub-surface magnetic fields that affect the f-mode, invisible in the surface B_rms which was used as the selection criterion for really quiet patches. This is illustrated in Fig. 8, where we show the measured f-mode energy versus the B_rms in the patches. The f-mode energy is not correlated with the B_rms seen at the surface, and strong, nearly constant, variability is seen at different epochs of the solar cycle. This poses clear limitations of the calibration method proposed here to detect weak transient signals in the f-mode evolution.

Fig. 8. f-mode energy as a function of Brms for the most quiet patches at disk center. The colors indicate the grouping according to the years. The standard deviation for the f-mode variation is 87.

Figure 7 displays the butterfly diagram of the QS f-mode energy determined from 15° ×15° patches that showed only weak, small-scale magnetic structures. To compute the f-mode energy, we have used the whole ring diagram data. Temporally averaged profile in latitude is removed for highlighting the variation in the f-mode power. The period covered is somewhat larger than the 11 year SC24, which began to show some magnetic activity from early 2010; this cycle had ended by around 2020 (see also the lower panel of Fig. 9, showing the sunspot number of SC24 and SC25 up to the writing of this manuscript). Broadly, we find an anti-correlation of the f-mode energy with the activity cycle of the Sun – during the solar minimum and early rising phase (∼2010−2012), the f-mode energies are greater, and around cycle maximum to the declining phase, the f-mode energy is suppressed. This correlation is strongest near the solar equator, within about ±20° in latitude, and it decreases with higher latitudes. Interestingly, we observe a temporal shift in the f-mode butterfly diagram with respect to the solar cycle, such that the minimum of the f-mode occurs later, namely, in the declining phase of SC24, which is roughly around the end of the year in 2016.

Fig. 9. Selected latitudinal cuts through the butterfly diagram and their comparison to the sunspot number. Top: cut through butterfly diagram of f-mode energy variation for three different latitudes (see legend). The solid lines represent a fit using a sine function. Bottom: NOAA sunspot number.

In mid-2017, we see weak strengthening of the f-mode strength to commence, first occurring at higher southern latitudes. During the minimum (2018–2019) between the SC24 and 25, the strengthening appears stronger in the higher latitudes. It also continues after the minimum, when SC25 has already started its ascending phase. What is also noteworthy is that the f-mode energy never rises as high as the values observed during the ascending phase of SC24 (2011–2012).

In Fig. 9, we present cuts through the butterfly diagram at three different latitudes, equator, and ±29°, and sinusoidal fits to the data points. The variability is strongest at the equator, but also contains the largest scatter. The minimum f-mode energy is obtained around the beginning of the year 2018. There, the difference in magnitude during SC24 and 25 is the largest. Southern higher latitudes show very weak variation in contrast to the equator, while the northern one has an intermediate magnitude. The shift with regard to the solar cycle is somewhat latitude-dependent. At the higher northern latitude, the f-mode minimum occurs roughly a year earlier than at the equator. The shift in the f-mode mode phase with regard to the sunspot cycle is on the order of three to four years, hence, it is more in phase with the poloidal phase of the magnetic field than the toroidal one.

3.2. AR f-mode with QS calibration

In this section, we compare the f-mode time evolution before and after the emergence of two ARs (11130 in Fig. 10 and 11105 in Fig. 11) that were reported to show an enhancement both in Singh et al. (2016) and Waidele et al. (2022) with regard to a QS control patch in the opposite hemisphere several days before their emergence. The main difference in our analysis is that the f-mode energy is now normalized to the actually measured average QS level around the specific time and latitude. To minimize the QS fluctuations, a Gaussian smoothing to the QS E_f, is applied, but the smoothing kernel width used is kept at 5° in longitudinal and latitudinal direction so that the fit to the data can be considered accurate. The f-mode energy of 1 is thus equivalent to that of the QS, and values that are stronger (weaker) indicate an enhancement (quenching) of the f-mode with regard to QS. Another difference is that we use the full ring diagram when computing the f-mode energy, while the other papers used only k_x = 0 cuts. However, we performed analyses with k_x = 0 and k_y = 0 cuts and saw no significant difference between the two, nor with regard to the full ring data, except for the increased noise level in E_f, derived from single cuts. As the measurement is done exactly in the same manner for the QS and ARs, we still anticipate that this difference should not influence the results significantly. Also, as more integrations are performed, the less noisy the signal, thus improving the data quality.

Fig. 10. Calibrated f-mode strength ($\stackrel{\sim }{E_f}$, top), QS calibration data (Ef, gray dots) and fits (middle), and Brms (bottom) for AR11130. The line-plot colors in the top and the middle panel indicate $\stackrel{\sim }{E_f}$ and Ef for various calibration methods as indicated in the legend. The shaded area in the top panel represents the standard deviation of the QS calibration derived from Fig. 8 and scaled with the fitted calibration functions.

Fig. 11. Calibrated f-mode strength ($\stackrel{\sim }{E_f}$, top), QS calibration data (Ef, gray dots) and fits (middle), and Brms (bottom) for AR11105. The color and labeling scheme is the same as in Fig. 10.

The results from our AR analysis are shown with green symbols and lines in Figs. 10 and 11: in the top panel, each orange point shows the normalized f-mode energy, $\stackrel{\sim }{E_f}$, with four-hour cadence, smoothed with a 24-h boxcar to remove a daily fluctuation otherwise prominently present in the HMI data. The shaded areas show the QS variance, $E_f^{\prime }$, determined from the standard deviation of the variation presented in Fig. 8, is roughly constant (around 4–5%) at all latitudes and longitudes. When it is used as normalization of the f-mode, then the uncertainty at large longitudes becomes very high, as is indicated by the rapidly fanning shaded areas toward the limbs. The B_rms measured simultaneously at the surface is shown in the lowest panels of the figures with black symbols.

In the middle panels of Figs. 10 and 11, we compare the different calibration curve candidates. The calibration curve used by Singh et al. (2016), based on more simple cosinus dependence of the form cosα[q+(1−q) cos α] with q = 0.5 and cosα = cosλcosφ, is shown with blue symbols and lines in the aforementioned panels. As this specific curve does not fit the QS data very well, we also performed a fit and determined the optimal value of q, that turns out to be −0.045; this curve and calibration with it are plotted with orange symbols and lines in the top and middle panel of the figures. The differences between these calibration curves are illustrated in the middle panels; in particular, the Singh et al. (2016) calibration curve does not fit the data (overplotted with gray dots) well at larger longitudes. There, we can see it is decreasing less strongly than shown by the data. Near the disk center the amplitude is too low to present the data well. The new cosinus fit and the Gaussian convolution applied to the QS data represent it better, with the consequence that the calibration curves decrease more steeply toward the limbs. The fitted cosinus curve has somewhat larger amplitude than the Gaussian convolution. This has the effect that the $\stackrel{\sim }{E_f}$ calibrated with the cosinus fit tends to be always below the QS level. The Gaussian convolution calibration results at $\stackrel{\sim }{E_f}$ values maximally at the QS level before the AR emergence.

As can be seen from the top panels of Figs. 10 and 11, applying the new QS calibration curve flattens the signal profile in comparison to the earlier q = 0.5 calibration used. For both of the selected ARs, the f-mode energy close to the limb is below the QS level to start off with, which could indicate that both of these active regions occur in an environment already affected by a sub-surface magnetic field. Applying the earlier calibration curve, a clear enhancement above the QS level is visible for AR11130, while for AR11105 the profile is similar, but the enhancement amplitude remains within the level of QS variability (shaded area). The new calibration shows a more modest enhancement, reaching its peak value at similar times as with the earlier calibration for AR11130, while somewhat earlier for AR11105, but its amplitude does not exceed the QS level significantly. Unfortunately, the possible enhancement of f-mode energy of the selected ARs occurs so close to the limb that it is not entirely clear whether it is an artifact of the rather uncertain limb calibration data or a true effect. Obviously, a larger sample size should be studied, which would also include ARs that emerge closer to the west limb to adequately substantiate or refute this scenario.

4. Discussion and conclusions

The first part of this paper presents an analysis of QS magnetism, where the main findings are the independence of the solar cycle with regard to the internetwork magnetic fluctuations, studied by using 1° patches, while network and internetwork fields, studied by using 15° patches, were found to show a statistically significant solar cycle dependence. The maximum of the magnetic fluctuations at the disk center was observed to exhibit a phase shift of roughly half a year w.r.t. to the sunspot-number-defined cycle. We interpret these findings in the following.

The independence of the internetwork magnetic fields either reflects the fact that these fields, clearly on smaller scales than the supergranular cells, are generated by the fluctuation (or small-scale) dynamo alone, or then the sensitivity of the HMI instrument prevents any variations from being seen. The solar cycle dependence of the network and internetwork fields reflects the fact that two separate processes are responsible for generating these fields. Turbulence is tangling the solar-cycle dependent large-scale sub-surface field resulting in magnetic fluctuations that have the same dependence, and these are then expelled to the edges of the supergranular cells. The magnetic fluctuations generated by the fluctuation dynamo also become expelled in a similar fashion, but as the growth of these fluctuations is exponential due to the dynamo instability, the fluctuation dynamo can quickly replenish the fluctuations also in the internetwork regions. The tangling process can be envisioned to have an amplification time scale that is slower and only linear over time.

As extensively reviewed in Brandenburg & Subramanian (2005), in turbulent dynamo theory, the magnetic fields grow under the constraint of magnetic helicity conservation, which leads to a bihelical spectrum of magnetic helicity. Signs of such bihelical nature of the solar surface magnetic field have already been reported by Brandenburg et al. (2017), Singh et al. (2018). The accumulation of small-scale magnetic helicity leads to the quenching of large-scale dynamo. In order to further grow its large-scale magnetic field, the system must shed its small-scale helicity. Being an open system, the Sun may have fluxes of magnetic helicity where ARs could play a vital role in removing the magnetic helicity from small-scales, thus leading to a rejuvenation of the large-scale dynamo. This mechanism was proposed to lead to a phase shift between the cycles for sunspot and magnetic helicity, that was seen to peak half a year later than the sunspot cycle in Singh et al. (2018). We see similar evidence here for the solar-cycle dependent part of the magnetic fluctuations in the network and internetwork – the phase shift by half a year is consistent with the large-scale field being rejuvenated later, when ARs have already peaked, shedding some small-scale magnetic helicity out from the system to allow for the growth of the global field.

The second part of our study describes how we built a novel method for calibrating the f-mode energy using the very quiet patches harvested in the first part. Even though more than 22 000 patches were analysed to obtain the statistics over the solar cycle, the f-mode energy variations of the QS remained broad, while showing no clear correlation with the rms magnetic field strength measured at the surface. We interpret this as an indication of the f-mode energy being affected by sub-surface magnetic fields, and the surface rms magnetic field being an inadequate indicator to find the QS level. The measured QS f-mode energy, indeed, shows a solar-cycle variation, which is, in broad terms, anti-correlated with the solar cycle, the f-mode energy being lower (higher) when the rms magnetic field is strong (weak). Such a behavior is expected in the light of many previous investigations, which have suggested f-mode damping to occur as a result of absorption of the f-mode mode by the magnetic fields in ARs (Cally et al. 1994; Cally & Bogdan 1997; Singh et al. 2016). This effect is the dominant one over the possible enhancement prior to AR emergence, as can be seen also in the hindcasted AR data in this study. Combined with the heavy averaging, any possible enhancement will be washed out from a statistic measuring the global behavior.

The phase shift of several years between the sunspot cycle and the f-mode modulation is too large to be explicable by the scenario suggested above for the half a year phase shift of the QS magnetism maximum w.r.t. the sunspot cycle. The f-mode energy modulation appears to follow more closely the poloidal component of the global field than the toroidal part that is commonly thought to give rise to the ARs. These two field components are known to have a systematic phase difference of roughly π (see, e.g., Charbonneau 2010).

The general trend of the f-mode energy being reduced during SC25 in comparison to SC24 could be a result of instrumental aging, but the clear differences seen over different latitudes and hemispheres is an argument that disfavors an overall instrumental degradation. If it were a physical effect, it would suggest that the sub-surface magnetic field is stronger during the ascending phase of SC25 than that of SC24, and that could lead to SC25 being stronger than SC24. Further investigations and fine tuning of the method are required to verify the results and conclusions reached in this study, however, the QS f-mode energy seems to have potential applications in diagnosing the sub-surface magnetic fields in the Sun.

The third and last part of our study present two hindcasted AR f-mode signals that have been proposed to show a clear enhancement of the f-mode energy in the earlier studies (Singh et al. 2016; Waidele et al. 2022), with our novel QS calibration method. In summary, our analysis shows that the transient and weak enhancement signal is very sensitive to the calibration method used. The new method for the QS calibration developed here tends to show a more flat signal with mild enhancement only in comparison to the earlier calibration method of Singh et al. (2016). Although a signature of an enhancement is seen in general, it remains unclear whether it is an effect caused by the uncertainties close to the limb or a real effect. In the light of the QS data, the magnitude of the enhancement is weaker than the QS variability level and, hence, its detection and usage as an AR emergence predictor is not possible with the QS calibration method.

Acknowledgments

We are indebted to Dr. Harsha Raichur, the developer of the original f-mode analysis pipeline, wherefrom this work stems. We also acknowledge the fruitful discussions with Prof. Nishant Singh on the theoretical interpretation of the results and practical insights to the analysis. All SDO data used are publicly available from the Joint Science Operations Center (JSOC) at Stanford University supported by NASA Contract NAS5- 02139 (HMI), see http://jsoc.stanford.edu/. The data analysis has been carried out on supercomputers in the facilities hosted by the CSC – IT Center for Science in Espoo, Finland, which are financed by the Finnish ministry of education. The data were also processed at the German Data Center for SDO (GDC-SDO), funded by the German Aerospace Center (DLR), and hosted by the Max Planck Institute for Solar System Research (Göttingen, Germany). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Project UniSDyn, grant agreement no 818665).

References

All Figures

Fig. 1. Data pipeline deployed in the CSC HPC environment. The leftmost tree illustrates the pipeline to collect the magnetograms in the most quiet patches, while the rightmost one the pipeline to track data from the quiet patches from the HMI database, and compute the f-mode energy. The central path of AR processing is otherwise equivalent to the QS pipeline, but their AR coordinates are sent for tracking in the MPS (in Germany) cluster environment, followed by an additional step, namely, QS calibration, at the end. Rectangular boxes represent analysis functions and ellipsoids are the derived data products. The rectangles with yellow frames stand for the corrective functions applied to the data.

In the text

	Fig. 2. Determination of the correction for the HMI sensitivity change: observing mode change on 13 Apr. 2016 causes a discontinuity in the level of Brms values of the internetwork data. The original data are displayed with the dark red and black dots, the corrected data with the light red dots. The dashed line indicates the polynomial fit of a degree of 3 used to obtain the offset.
In the text

Fig. 3. Examples of a typical QS f-mode spectra. Top: example of QS ring diagram at the angular frequency ν = 3.57 mHz for one quadrant of the full ring (logarithmic color scale), computed from the data cube presented in Fig. 4 (left panel). Bottom: collapsed spectrum obtained by integrating over the ring diagram. The red vertical line marks the position of the maximum of the f-mode and the black vertical lines the range of integration. The wavenumber k is expressed in units of the circumference of the Sun (CSun).

In the text

	Fig. 4. Comparison of two disk-center magnetograms at solar minimum (21 Jul. 2010) and around the maximum seen in the disk-center Brms values (09 Nov. 2014). The maps show the first frame of the 8 h data cube.
In the text

Fig. 5. Brms determined from the most quiet patches from 2010 to 2022 at disk center. The patches of 15° size in longitude and latitude contain network and internetwork fields. The solid red lines display the 97% percentile level, the dashed gray line the mode of a log-normal fit to yearly-binned data moved in a sliding window of 100 days length. For all values of ω, the magnitude of P is always an order of magnitude higher than the noise level outside the considered location of the ring.

In the text

Fig. 6. Brms determined from the most quiet patches from 2010 to 2022 at disk center, but in contrast to Fig. 5, the patch size was 1° in longitude and latitude, corresponding to internetwork patches. The color and labeling scheme is the same as in Fig. 5. For all values of ω, the magnitude of P is always an order of magnitude higher than the noise level outside the considered location of the ring.

In the text

Fig. 7. Butterfly diagram of f-mode energy variations, $E_f^{\prime }(\lambda ,t)$, computed from the collapsed ring diagrams (see bottom panel of Fig. 3). The temporal average, $\overline{E_f}(\lambda )$, has been subtracted from the data, and is shown as the black line in the right panel. Its error bars represent the time-averaged standard deviation of the fluctuations of the f-mode energy around the signal for every bin ($\overline{\sigma }(\lambda )$).

In the text

	Fig. 8. f-mode energy as a function of Brms for the most quiet patches at disk center. The colors indicate the grouping according to the years. The standard deviation for the f-mode variation is 87.
In the text

	Fig. 9. Selected latitudinal cuts through the butterfly diagram and their comparison to the sunspot number. Top: cut through butterfly diagram of f-mode energy variation for three different latitudes (see legend). The solid lines represent a fit using a sine function. Bottom: NOAA sunspot number.
In the text

Fig. 10. Calibrated f-mode strength ($\stackrel{\sim }{E_f}$, top), QS calibration data (Ef, gray dots) and fits (middle), and Brms (bottom) for AR11130. The line-plot colors in the top and the middle panel indicate $\stackrel{\sim }{E_f}$ and Ef for various calibration methods as indicated in the legend. The shaded area in the top panel represents the standard deviation of the QS calibration derived from Fig. 8 and scaled with the fitted calibration functions.

In the text

	Fig. 11. Calibrated f-mode strength ($\stackrel{\sim }{E_f}$, top), QS calibration data (Ef, gray dots) and fits (middle), and Brms (bottom) for AR11105. The color and labeling scheme is the same as in Fig. 10.
In the text