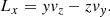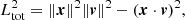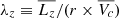| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202243926 | |
| Published online | 03 November 2022 | |
Testing the robustness of DYNAMITE triaxial Schwarzschild modelling: The effects of correcting the orbit mirroring
1
Department of Astrophysics, University of Vienna, Türkenschanzstraße 17, 1180 Vienna, Austria
e-mail: sabine.thater@univie.ac.at
2
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
3
Department of Astronomy and Space Sciences, University of Chinese Academy of Sciences, 19A Yuquan Road, Beijing 100049, PR China
4
Leibniz-Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
5
School of Physics, University of New South Wales, NSW 2052, Australia
6
ARC center of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Sydney, Australia
7
Center for Extragalactic Astronomy, University of Durham, Stockton Road, Durham DH1 3LE, UK
8
Sterrewacht Leiden, Leiden University, Postbus 9513, 2300 RA Leiden, The Netherlands
9
Max Planck Institute for extraterrestrial Physics, Giessenbachstraße 1, 85748 Garching, Germany
10
SDB Science-driven Business Ltd, 85 Faneromenis Avenue, Ria Court 46, Suite 301, 6025 Larnaca, Cyprus
11
DiSAT, Università degli Studi dell’Insubria, via Valleggio 11, 22100 Como, Italy
12
INAF, Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy
13
INFN, Sezione di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
14
European Space Agency, European Space Research and Technology Centre, Keplerlaan 1, 2200 AG Noordwijk, The Netherlands
Received:
2
May
2022
Accepted:
8
August
2022
In the past 15 yr, the triaxial Schwarzschild orbit-superposition code developed by van den Bosch and van de Ven in Leiden has been widely applied to study the dynamics of galaxies. Recently, a bug was reported in the orbit calculation of this code, specifically in the mirroring procedure that is used to speed up the computation. We have fixed the incorrect mirroring in the DYNAMITE code, which is the publicly-released successor of the Leiden triaxial Schwarzschild code. In this study, we provide a thorough quantification of how this bug has affected the results of dynamical analyses performed with this code. We compare results obtained with the original and corrected versions of DYNAMITE, and discuss the differences in the phase-space distribution of a single orbit and in the global stellar orbit distribution, in the mass estimate of the central black hole in the highly triaxial galaxy PGC 46832, and in the measurement of intrinsic shape and enclosed mass for more than 50 galaxies. Focusing on the typical scientific applications of the Schwarzschild method, in all our tests we find that differences are negligible with respect to the statistical and systematic uncertainties. We conclude that previous results with the Leiden triaxial Schwarzschild code are not significantly affected by the incorrect mirroring.
Key words: galaxies: kinematics and dynamics / galaxies: structure / quasars: supermassive black holes
© S. Thater et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Dynamical modelling is a powerful technique to study the evolution of galaxies. Traditionally this approach was restricted to spherical and axisymmetric models with analytic distribution functions depending on the integrals of motion E and Lz (e.g., Nagai & Miyamoto 1976; Satoh 1980; Qian et al. 1995; Magorrian et al. 1998). Observational evidence and numerical investigations showed that such models do not capture the full solution space (e.g., Binney 1982). A popular alternative is to use the Jeans (1922) equations which connect the velocity dispersions to the mass density and gravitational potential, however without the assurance that the resulting models have a non-negative distribution function (Cappellari 2008, 2020).
Schwarzschild (1979) sidestepped explicit reliance on the integrals of motion or on the Jeans equations by numerically solving the problem of populating the large variety of orbits in an assumed potential in such a way that it reproduces the mass density. As the orbits and the number of stars on it are known, the distribution of stars over position and velocity is then known everywhere in the model. The orbit occupation numbers are therefore the equivalent of the phase-space distribution function f(x, v)≥0 that is the solution to the collisionless Boltzmann equation. Elliptical galaxies can broadly be described by cored triaxial density distributions. Schwarzschild (1982) demonstrated that these triaxial density distributions can be in dynamical equilibrium, even when the figure of the system is allowed to rotate slowly. Merritt & Fridman (1996) constructed triaxial systems with central density cusps in this way.
Since this early work, Schwarzschild’s orbit superposition method has been extended to include kinematic data (e.g., Richstone & Tremaine 1984; Rix et al. 1997; van der Marel et al. 1998; Cretton et al. 2000), and has been applied to spherical, axisymmetric and triaxial models with a dark halo and a central density cusp plus supermassive black hole. Rather than deprojecting the observed galaxy properties, the comparison with the numerical model is done in the observed plane, by calculating the line-of-sight integrated properties for each orbit, including, e.g., the effect of finite detector pixels, seeing convolution and internal extinction. When only the surface density is given, the solutions are non-unique (e.g., Rybicki 1987; Gerhard & Binney 1996). Adding kinematic constraints shrinks the range of solutions, which are computed for a range of assumed black hole masses or halo profiles. The resulting distribution of stars in phase space in many cases reveals significant structure, which reflects the different components in the observed galaxy. This decomposition is not done ad-hoc on, e.g., the surface brightness profile, but is done in phase space, constrained by all the observables, and allows exploring the formation history of the galaxy. Alternatives to Schwarzschild’s method include the made-to-measure models of Syer & Tremaine (1996), de Lorenzi et al. (2008), Bovy et al. (2018).
In the past two decades, the Schwarzschild method has been applied to multiple galaxies, initially in axisymmetric geometry and more recently also in triaxial geometry, to study their internal stellar structure (e.g., Thomas et al. 2007; Cappellari et al. 2007; van de Ven et al. 2008; Feldmeier-Krause et al. 2017; Poci et al. 2019; Jin et al. 2020; Santucci et al. 2022; Pilawa et al. 2022), to determine their dark matter (DM) content (e.g., Thomas et al. 2007; Cappellari et al. 2013; Poci et al. 2017; Santucci et al. 2022), to weigh their central massive black holes (e.g., van der Marel et al. 1998; Verolme et al. 2002; Gebhardt et al. 2003; Valluri et al. 2004; Gebhardt & Thomas 2009; Krajnović et al. 2009, 2018; Walsh et al. 2012; Rusli et al. 2013; Thater et al. 2017, 2019, 2022; Ahn et al. 2018; Mehrgan et al. 2019; Liepold et al. 2020; den Brok et al. 2021; Roberts et al. 2021; Pilawa et al. 2022) and to identify accreted galactic components (e.g., Zhu et al. 2020, 2022; Poci et al. 2021).
Independent implementations of the triaxial Schwarzschild method include van den Bosch et al. (2008), Vasiliev & Valluri (2020) and Neureiter et al. (2021). These typically use numerically computed orbit libraries on the order of 105 orbits. The linear combination of these orbits is found which best represents the observed kinematics and luminosity of the galaxy under study. Each of the modelling steps requires a careful handling of state-of-the-art data and the use of high-performance computing to facilitate expensive calculations. In order to minimise the computational costs, the Schwarzschild code by van den Bosch et al. (2008) exploits the symmetries of the assumed galaxy potential. In a stationary, non-rotating, triaxial potential, the orbital properties are computed in one octant of phase-space, and then the remaining seven octants are filled by mirroring the orbits.
Recently, Quenneville et al. (2022) pointed out that the triaxial Schwarzschild code released by van den Bosch et al. (2008) contained a bug whereby some orbit types were mirrored incorrectly. They derived the correct mirroring scheme, and tested the effect of this correction on models of the galaxy NGC 1453, finding significant changes to the χ2 distribution and best-fit parameters. This raised some concern about previously published results that were obtained with the code by van den Bosch et al. (2008). In this work, we quantify the effect of the bug on a variety of scientific applications. We formed a collaborative team in which many members ran independent tests to obtain an unbiased, qualitative analysis.
The corrected code is available as DYNAMITE1 (Jethwa et al. 2020). This is the publicly released successor to the van den Bosch et al. (2008) code. The DYNAMITE framework provides a modern Python library with well-documented application programming interface and new functionality on top of the Schwarzschild code by van den Bosch et al. (2008). For example, DYNAMITE can accept kinematic inputs from the BAYES-LOSVD software (Falcón-Barroso & Martig 2021), which models the line-of-sight velocity distribution using a flexible, histogrammed description; this approach may be more suitable for complex distributions than the widely-used Gauss-Hermite expansions. DYNAMITE also supports various options for solving for orbit-weight solving, including the quadratic-programming approach extolled in Vasiliev & Valluri (2020).
This paper is organised as follows. In Sect. 2 we discuss the details of the bug and its correction. In Sect 3 we show the effect of the bug-fix on several physical parameters for a representative galaxy sample. In Sect. 4 we quantify the effect of the bug-fix for a recently published black hole mass measurement in the galaxy PGC 046832 (den Brok et al. 2021). The inferred global orbits distribution is discussed in Sect. 5. In Sect. 6 we conclude that previously reported results are not significantly affected by the mirroring bug, and we present an outlook to on-going research with dynamical modelling.
2. A detailed description of the orbit mirroring bug
Stationary, non-rotating, triaxial potentials are symmetric with respect to the three principal axes. Due to this eight-fold symmetry, in the Schwarzschild code all orbital properties of regular orbits only need to be calculated in one octant and can be mirrored to the other seven. This procedure makes it possible to quickly obtain orbits starting from all octants, while only computing directly orbits that originate in one, thereby saving computational time.
Regular orbits obey a point inversion symmetry in the shape of the orbit. Initial conditions are chosen in one octant and then integrated to obtain an orbit. This orbit is then mirrored in the other seven octants; if the orbit already had point symmetry then it is simply sampled more densely. However, although the spatial mirroring is always carried out identically for all orbit types, the velocity components need to be treated separately, due to the different conserved quantities associated with each orbit and the need to preserve them when the effective orientation of the orbit is flipped. Families of orbits are distinguished by which component of angular momentum, if any, they conserve. If there is no net (orbit-averaged) angular momentum conservation, or the net angular momentum is zero, then the orbit is a regular box orbit, so the signs of the mirrored velocity components just follow the signs of the coordinates. If the angular momentum component associated with the long axis is conserved, then it is a long-axis tube (LAT) orbit, and so in each octant the signs of vy and vz must be adjusted such that Lx remains unchanged, where
Similar considerations must be made for short-axis tube (SAT) orbits, which conserve Lz (sometimes a distinction is also made between inner- and outer-long-axis tube orbits, but this is not needed for the mirroring procedure). These sign changes are summarised in Table 1. In the incorrect mirroring scheme, four out of eight velocity components of short and long-axis tube orbits had a flipped sign, meaning that the resulting mirrored orbits did not all correspond to the same (regular) orbit, and consequently should not have shared the same weight.
Corrected orbit mirroring scheme.
We analysed hundreds of individual orbits under the correct and incorrect mirroring scheme, calculated for two different galaxy potentials: a triaxial potential and a potential in the axisymmetric limit. The triaxial potential uses the luminosity model of PGC 046832 by den Brok et al. (2021) and the potential in the axisymmetric limit was derived from the luminosity model of the simulated Auriga galaxy halo 6, which was published in Zhu et al. (2020). The second potential is close to axisymmetric as the galaxy disk dominates, but triaxiality is allowed in the model. The results of the triaxial potential are explained in the main text, while we describe the axisymmetric case in Appendix A.
Figures 1 and 2 show the impact of the incorrect orbit mirroring for a single orbit. We choose a typical short-axis tube (SAT) orbit in the model with triaxial potential2. As shown in Table 1, for SAT orbits, four out of eight octants had a vz velocity component with an incorrect sign. The top left panel of Fig. 1 shows that the total angular momentum of these four incorrectly mirrored orbits (red line) was not equal to that of the base orbit (grey line). After the correction (blue dotted line), this problem is solved.
 |
Fig. 1. Impact of the incorrect orbit mirroring for a single orbit. We show a typical short-axis tube orbit derived in the triaxial potential by den Brok et al. (2021). The four panels show the evolution of Ltot (top left), Lz (top right), Lx (bottom left) and Ly (bottom right). The original orbit, correct (‘bug-fix’) and incorrect (‘nofix’) mirrors are shown by gray, blue, and red colours, respectively. We only show the four mirroring cases (out of eight) that are changed compared to the original code (see Table 1). In one panel, rows from top to bottom represent the 2nd, 3rd, 6th, and 7th mirrors, respectively. We show the orbit for only 25 (out of 200) revolutions to avoid crowding. The time of one orbital period is ∼0.06 Gyr. |
 |
Fig. 2. Impact of the incorrect orbit mirroring for a single orbit. We show a typical short-axis tube derived in the triaxial potential by den Brok et al. (2021). Columns from left to right show the orbit trajectories, the line-of-sight mean velocity V with the correct (‘bug-fix’) and incorrect mirroring (‘nofix’) and the relative error between the incorrect and correct mirroring schemes ΔV/V, the velocity dispersion σ with the correct (‘bug-fix’) and incorrect mirroring (‘nofix’) and the relative error. Rows from top to bottom refer to different inclination angles of 15°, 45° and 75°, respectively. The changes in the mean velocity and velocity dispersion are up to ∼40% in some regions of the orbit space, but they are usually ≲10% in regions where the star spends most of its life. |
Although the total angular momentum of mirrored orbits must be equal to that of the base orbit, individual components of the angular momentum may or may not change under mirroring. For a SAT orbit, which circulates around the z axis, we expect all mirrored versions to have the same Lz as the base orbit. The top right panel of Fig. 1 shows that this is true both for the original and corrected codes. This is in accordance with Table 1: since only vz was incorrect for SAT orbits, the z component of the angular momentum stays unchanged by the bugfix. The other two components can change under mirroring, but the changes must be consistent with unchanged Lz and Ltot. This varies by octant: for the second mirror, for example (top row of all panels), Lx is flipped relative to the base orbit while Ly is unchanged. In order to preserve Ltot the mirroring should only ever induce sign-changes in components of the angular momentum. This is because, while Ltot is invariant with respect to sign-flips in the individual angular momentum components Li, it is not invariant with respect to arbitrary sign-flips in the individual velocity components vi. This can be seen from the formula
which implies that Ltot is preserved only if the combinations (xLx, yLy, zLz) each have the same overall sign-flip. The short-period oscillations in the ‘nofix’ versions of Lx and Ly are consequences of the incorrect mirroring, the exact cause of which is unknown but which is probably due to Lx and Ly no longer being constrained by the overall conservation of Ltot.
In Fig. 2, we show the trajectories of the same SAT orbit as in Fig. 1. The trajectories were integrated for 200 times the orbital period, and we sample 50 000 particles from it with equal time steps. We project the orbit with inclination angles of 15° (near face-on), 45° and 75° (near edge-on). For all cases, we fixed ϕ (rotation of orbits around the intrinsic minor axis) to be 0° and ψ (rotation of projected orbits with respect to the Y′ axis in the sky plane) to be 90°. So only the inclination θ (rotation of orbits around the intrinsic major axis) is changing. The projected mean velocity and velocity dispersion maps of the orbit when considering the correct (‘bugfix’) and incorrect (‘nofix’) mirroring are shown for comparison in Fig. 2; the spatial distribution of the orbit does not depend on the mirroring of the velocity components, thus we only show it once.
Figure 2 shows that (for this orbit) the relative error in mean velocity and velocity dispersion can reach ∼40% in some regions, consistent with the findings of Quenneville et al. (2022). Note however that the regions with large difference are mostly those with very low surface density of the particle. The changes are usually small (≲10%) in regions of the orbit space where the star spends most of its life, and this is true for all projections. We do note that for some orbits and some viewing angles there are larger deviations between the two models for very small radii, where the surface density is higher. We think that these are driven by low velocities in the kinematics. Comparing different projections, we see that the largest errors occur for an intermediate inclination of 45°. This is somewhat surprising for this SAT orbit where only vz has changed: the naive expectation would be that the face-on view shows the largest error, decreasing monotonically to the edge-on view. This naive logic fails to account for the fact that vz flips sign frequently throughout this orbit. For the face-on case, the incorrect sign introduced by the bug is on average cancelled out by the repeated sign-flips of the orbit. For the exactly face-on and edge-on cases, we have confirmed that this orbit shows no change in its kinematic-maps after the bug-fix.
Having inspected one single orbit here, it is important to remember that Schwarzschild models are typically built from thousands of orbits. We therefore investigate in the following section, whether this change of mean velocity and velocity dispersion within a single orbit also introduces significant changes in the inferred best-fit parameters of the Schwarzschild models that use several thousands of orbits.
3. Enclosed mass and shape parameters
Although the construction of triaxial Schwarzschild models is computationally expensive, it has become feasible to study the dynamics of large galaxy samples (Zhu et al. 2018a; Jin et al. 2020; Santucci et al. 2022). In order to investigate potential systematic biases due to the incorrect mirroring, we collected data from several galaxy surveys and ran the triaxial Schwarzschild code with the correct and incorrect mirroring scheme. While the previous studies had heterogeneous model setups (i.e. different numbers of orbits, different MGE assumptions), we ensured that each individual galaxy was run in the same original setup for the correct and incorrect mirroring. Our analysis shows no significant discrepancies in the inferred enclosed mass and in the shape parameters of the studied galaxies. Furthermore, differences in the stellar orbit distribution caused by the incorrect mirroring are negligible compared to other systematics.
Unless otherwise stated, all models in this section are run with six free parameters: the stellar mass-to-light ratio M*/L, intrinsic stellar axis-length ratios p (long-to-short) and q (intermediate-to-short), the stellar projected-to-intrinsic scale-length ratio u, dark matter virial mass M200, and the dark matter concentration c. The shape of the dark matter halo is assumed to be spherical as currently implemented in DYNAMITE.
3.1. The sample
Our studied galaxy sample is a combination of 25 passive galaxies from the SAMI survey Data Release 3 (Croom et al. 2021), 18 early-type galaxies (ETGs) from the ATLAS3D survey (Cappellari et al. 2011) and 12 ETGs and late-type galaxies (LTGs) from the Fornax3D survey (Sarzi et al. 2018). We added six additional galaxies from miscellaneous other works: FCC 47 (Fahrion et al. 2019, Thater et al., in prep.), ESO286-G022 (Poci & Smith 2022), PGC 046832 (den Brok et al. 2021) and Auriga simulated galaxy halo 6 at inclinations 40°, 60° and 80° (Zhu et al. 2020). The six additional galaxies were run with the corrected and uncorrected mirroring following the specifications in the respective publications.
Our SAMI galaxies are a subset of the sample by Santucci et al. (2022) who used the van den Bosch et al. (2008) triaxial Schwarzschild code to study the inner orbital structure and mass distribution of 161 passive galaxies. We want to emphasize that in the published work by Santucci et al. (2022) the triaxial Schwarzschild code with corrected mirroring is used. For this study, we randomly chose a subset of 25 galaxies from these galaxies with kinematic data signal-to-noise S/N > 15 and best-fit model reduced χ2 < 3.0. These criteria are adopted to avoid getting strong parameter biases due to galaxies with weak kinematic constraints or poor fit quality. We then used the same DYNAMITE setup for the dynamical models as in Santucci et al. (2022) but with correct and incorrect mirroring.
The subset of the ATLAS3D galaxy sample considered here was modelled with the goal to study the inner orbital structure in massive galaxies (Thater et al., in prep.) and the nature of counter-rotating galaxies (Jethwa et al., in prep.). We obtained the photometric data (Scott et al. 2013) and up to h4 kinematic maps (Cappellari et al. 2011) directly from the ATLAS3D webpage3. The Schwarzschild models were run in the same setup as described in Santucci et al. (2022) using an orbit library of 21 × 10 × 7 for both tube and box orbits with a dithering of 53. We fixed the dark matter concentration c with the M200 − c relation by Dutton & Macciò (2014) to get a better handle on the degeneracy between the stellar mass-to-light ratio M*/L and the dark matter distribution. The ATLAS3D kinematics do not have the spatial resolution to constrain the central black hole mass MBH, therefore we fixed its mass using the published effective velocity dispersion σe (Cappellari et al. 2013) and the empirical MBH − σe relation by van den Bosch (2016). All models were run with the same setup for the correct and incorrect mirroring.
Finally, six ETGs and six LTGs come from the Fornax3D survey and were modelled to understand the effect of the cluster environment on the growth of cold disks (Ding et al., in prep.). We obtained the kinematics from Iodice et al. (2019). The Fornax3D galaxies have very high-quality kinematic data: high spatial resolution; a high quality of V, σ, h3 and h4 and large kinematic data coverage (out to at least 2Re). The sample includes galaxies with morphology from highly disk-dominated to triaxial bulge dominated. Similar to the ATLAS3D galaxies, the black hole mass was fixed using the MBH − σe relation by van den Bosch (2016) and the dark matter concentration was fixed via the M200 − c relation. We sampled the orbits with 55 × 11 × 11 for both box and non-box orbits with dithering 53.
Thus, we were able to directly compare the two different code versions over more than 50 galaxies of very diverse morphology, data quality and coverage, as well as Schwarzschild model complexity (orbit library size, fitted parameters). From a grid search of our dynamical models, we derived the best-fit parameters for each of our galaxies for the correct and incorrect mirroring. We investigated the recovered viewing angles for all 61 galaxies. Because a single survey does not sample well all viewing angles, we consider three different surveys in this study. The full set of galaxies samples well the different viewing angles: The galaxies have θ (rotation of orbits around the intrinsic major axis) ranging from 40° and 90°, ϕ (rotation of orbits around the intrinsic minor axis) between 20° and 90°, and all galaxies have ψ of about 90°.
3.2. Comparison of correct and incorrect mirroring
In Figs. B.1–B.3 we show the derived kinematics for a galaxy from each of the considered surveys. These maps provide a direct comparison between the stellar kinematics obtained when using the correct and incorrect mirroring, and show that the differences induced by the incorrect mirroring are usually much smaller than differences between the models and the data. In Figs. 3 and 4 we show a comparison of the enclosed mass properties and galaxy shapes, respectively, for the full sample. The enclosed mass within one effective radius (Re) is very close to the 1–1 line for each of our galaxies, and thus extremely robust regarding the bug-fix. This robustness is independent of galaxy morphology, inclination or triaxiality. We want to stress here how remarkably consistent the enclosed mass measurements are, although we are using very different galaxy data sets.
 |
Fig. 3. Comparison of enclosed mass properties of our galaxy samples separated in total mass within one effective radius Mtot(< Re) (left panel) and stellar mass-to-light ratio M*/L (right panel) for correct (‘bugfix’) and incorrect (‘nofix’) orbit mirroring. The galaxy sample is a subset of Fornax3D LTGs and ETGs (green squares), SAMI passive galaxies (purple stars) and ATLAS3D ETGs (orange circles). Also added as black diamonds are the massive lensed ETG ESO286-G022 by Poci & Smith (2022), FCC 47 by Fahrion et al. (2019) and Thater et al. (in prep.), PGC 046832 by den Brok et al. (2021), which is also discussed in Sect. 4, and the three simulated LTGs by Zhu et al. (2020), which are discussed in Sect. 5. The dashed line shows the 1-1 line between the different versions. Both the derived total and stellar mass are not significantly affected by the incorrect mirroring of the orbits. Differences between the versions are within the reported statistical uncertainties of the dynamical modelling. Uncertainties were calculated by including all models within |
 |
Fig. 4. Comparison of inferred galaxy intrinsic shape parameters for our modelled galaxies. The galaxy sample is divided into Fornax3D LTGs and ETGs (squares), SAMI passive galaxies (stars) and ATLAS3D ETGs (circles). Also added as diamonds are the massive lensed ETG ESO286-G022 by Poci & Smith (2022), FCC 47 by Fahrion et al. (2019) and Thater et al. (in prep.), PGC 046832 by den Brok et al. (2021), which is also discussed in Sect. 4, and the three simulated LTGs by Zhu et al. (2020), which are discussed in Sect. 5. Both the intrinsic intermediate-to-major axis ratio p (left panel) and minor-to-major axis ratio q (right panel) show no significant change for the majority of the galaxies. There is no clear trend of increasing discrepancy with galaxy morphology or triaxiality T ≡ (1 − p2)/(1 − q2). Uncertainties were calculated by including all models within |
A similar behaviour is seen for the stellar mass-to-light ratio M*/L, albeit with a larger scatter due to its degeneracy with dark matter. This degeneracy is strong for ATLAS3D galaxies as the kinematics typically only cover about one Re and therefore we find the largest uncertainties for these galaxies. The M*/L derived with the incorrect mirroring scheme is within 10% of the M*/L with the correct mirroring, thus consistent within the M*/L uncertainty. We conclude that both enclosed mass and M*/L are very robust towards the incorrect mirroring. This is strong evidence that previous dynamical mass measurements are not significantly affected by the mirroring bug.
In Fig. 4, we show a comparison of the galaxy intrinsic shape parameters: the intrinsic intermediate-to-major axis ratio p = b/a, and the intrinsic minor-to-major axis ratio q = c/a. These parameters are much more difficult to constrain in dynamical models than the enclosed mass. Nevertheless, our comparison shows that p and q are robust against the incorrect mirroring. Almost all measurements are consistent within their uncertainties. Discrepancies are again independent of galaxy morphology, inclination or triaxiality parameter T = (1 − p2)/(1 − q2). As p and q enter T via their squares, the discrepancy in the derived T values shows more scatter than in either individual axis-ratio, but again there is no clear trend with galaxy properties. Some galaxies are more driven to a prolate shape, others more oblate, while others did not change. From this comparison, we conclude that galaxy intrinsic shapes in previous results likely do not suffer from systematic biases. We point out that intrinsic shape parameters depend on the quality of the data, and larger discrepancies are found for kinematic data with S/N < 20.
Table 2 summarises the results presented in Figs. 3 and 4. For each survey, we list in the table the mean ratios between best-fit parameters obtained before and after the bugfix for the mass to light ratio and for the p and q intrinsic shape parameters. In order to obtain these ratios we used the astropy package stats.biweight which is based on the method described in Beers et al. (1990). Most of these ratios have a deviation from unity of less than 5%, showing that the mirroring bug has not significantly affected the best-fit parameters. The only case in which a larger discrepancy (∼17%) is found regards the M*/L parameter for the Fornax3D galaxies. This discrepancy is driven by four of the 12 galaxies with very low M*/L because they are dark matter dominated.
Quantitative comparison of derived parameters with correct and incorrect mirroring.
4. A black hole mass estimate in a triaxial galaxy
den Brok et al. (2021) used the triaxial code of van den Bosch et al. (2008) in its original version to model the VLT/MUSE observations of PGC 046832. PGC 046832 is the brightest cluster galaxy in one of the sub-clusters of the Shapley Supercluster, at a distance of ∼200 Mpc. Because of its complex structure, this galaxy poses a challenge for modellers, requiring several inversions in the direction of its angular momentum and a radial change in triaxiality.
The dynamical modeling by den Brok et al. (2021) showed that a) the black hole mass determined with the triaxial Schwarzschild models was lower than the one determined using axisymmetric models and that b) the intrinsic shape of the galaxy changes from almost prolate in the centre to almost oblate in the outer parts. Here we show that correcting the orbit mirroring in the triaxial Schwarzschild code by van den Bosch et al. (2008) does not lead to a detection of the central supermassive black hole and only marginally changes the best-fit viewing angles. We also show the stellar orbit distribution (see also Sect. 5) of PGC 046832 in Fig. C.1. Changes in these plots compared to den Brok et al. (2021) are not significant.
4.1. Black hole mass
To determine the direct influence of the orbit mirroring correction on the black hole mass of PGC 046832, we assume the same viewing angles as used by den Brok et al. (2021) and the same dark matter halo mass. We re-run the Schwarzschild models in the exact same setup as in den Brok et al. (2021), but additionally supplement the grid with points at M/L between 2.9 and 3.0, as the χ2 contours imply a 4% lower M/L.
We show the χ2 contours in Fig. 5, where the contours from the correctly mirrored code are given in blue , and those from the incorrectly mirrored code in red. The red contours correspond to the black contours in Fig. 10 of den Brok et al. (2021). The correction of the orbit mirroring bug does not lead to a black hole detection. The derived M/L decreases by 4%, but this range is consistent within the 3σ confidence interval of the measurement. The blue contours are also noticeably more round than the red contours, indicating a change in the χ2 distribution. When inspecting the model kinematic maps of the best-fitting models, we did not notice any strong differences.
 |
Fig. 5. Contours describing the χ2 surfaces at different black hole masses MBH and mass to light ratios M/L. Red contours show the χ2 surface using the original version of the Schwarzschild code, and were previously presented in den Brok et al. (2021). Blue contours show the χ2 surface after correcting the mirroring bug in the code. Grey dots show the locations at which models were calculated. The thick contours contain models within |
4.2. Viewing angles
den Brok et al. (2021) assumed that the density of the galaxy could be modelled as a sum of aligned concentric Gaussians with different axis ratios pi and qi and scale lengths σi. This assumption allows an analytic deprojection of the observed light distribution given a set of viewing angles. Viewing angles therefore affect the gravitational potential in which orbits are calculated, and thus can be dynamically constrained. den Brok et al. (2021) used Schwarzschild models to constrain the viewing angles as (θ, ϕ, Ψ) = ( ,
, ,
, ) in degrees.
) in degrees.
We re-run Schwarzschild models with the same assumptions as in den Brok et al. (2021), i.e. fixed black hole mass and 3 different masses for the DM halo, to recreate the grid shown in their Fig. 6. We also explored the parameter space with a free DM halo mass and black hole mass using the same Gaussian sampling approach used in that paper. For the best-fit viewing angles we find (θ, ϕ, Ψ) = ( ,
, ,
,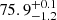 ), consistent with those obtained with the previous version of the code.
), consistent with those obtained with the previous version of the code.
The deprojection of the MGE using these new viewing angles does not lead to a significantly different intrinsic shape. After correcting the mirroring bug, a preference towards a massive black hole with mass log(MBH/M⊙)≲8 is still predicted by the fits. This does not mean that the new models shows no changes at all; the mass of the dark matter halo, expressed as a dimensionless scaling of the MGE mass, is higher than before ( versus
versus 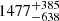 ), whereas the stellar M/L is somewhat lower (
), whereas the stellar M/L is somewhat lower ( versus
versus  ). The total galaxy mass within the radii that can be constrained by the kinematics is however consistent as was also found for other galaxies in Fig. 3. The changes on these quantities are likely caused by the intrinsic degeneracy between dark matter and stellar M/L, and the limited kinematic field-of-view that cannot constrain the dark matter very well.
). The total galaxy mass within the radii that can be constrained by the kinematics is however consistent as was also found for other galaxies in Fig. 3. The changes on these quantities are likely caused by the intrinsic degeneracy between dark matter and stellar M/L, and the limited kinematic field-of-view that cannot constrain the dark matter very well.
4.3. Other black hole mass measurements
Few black hole mass measurements have been derived with the triaxial Schwarzschild code by van den Bosch et al. (2008). It has been applied to the two mildly triaxial fast-rotating early-type galaxies M32 and NGC 3379 (van den Bosch & de Zeeuw 2010), the moderately triaxial early-type galaxy NGC 3998 (Walsh et al. 2012), the nuclear star cluster in the Milky Way (Feldmeier-Krause et al. 2017) and the ultra-compact dwarf galaxy M59-UCD3 (Ahn et al. 2018). Some of these studies resulted in black hole mass measurements that were inconsistent with other methods. Our investigation suggests that this inconsistency is not driven by the incorrect mirroring bug, but by other systematics, e.g. radially varying versus constant mass-to-light ratio (Thater et al. 2017, 2019, 2022), the inclusion of dark matter into the models (Gebhardt & Thomas 2009; Rusli et al. 2013; Thater et al. 2022) or other assumptions of the modelling techniques. Furthermore, the incorrect mirroring bug is not present in the Leiden version of the axisymmetric Schwarzschild code that was used to derive several black hole mass measurements (e.g., Krajnović et al. 2009, 2018; Thater et al. 2017, 2019, 2022, and the axisymmetric measurement in den Brok et al. 2021) . Cross-checks between the different code versions are extremely valuable to find systematic differences and mistakes in the codes.
5. Stellar orbit distribution
In addition to constraints on the gravitational potential, a useful result of Schwarzschild modelling is the stellar orbit distribution. This distribution is often shown in the space of circularity,  , i.e. the orbit angular momentum
, i.e. the orbit angular momentum 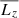 normalised by the angular momentum of a circular orbit with the same binding energy (Zhu et al. 2018b). This means that |λz| = 1 represents highly-rotating short-axis tube orbits (circular orbits), while λz = 0 represents mostly dynamically hot box or radial orbits. The circularity distribution has been used in the past to disentangle dynamical cold, warm and hot components and learn about the accretion history of nearby galaxies (e.g., Zhu et al. 2018b, 2020, 2022; Fahrion et al. 2019; Poci et al. 2019).
normalised by the angular momentum of a circular orbit with the same binding energy (Zhu et al. 2018b). This means that |λz| = 1 represents highly-rotating short-axis tube orbits (circular orbits), while λz = 0 represents mostly dynamically hot box or radial orbits. The circularity distribution has been used in the past to disentangle dynamical cold, warm and hot components and learn about the accretion history of nearby galaxies (e.g., Zhu et al. 2018b, 2020, 2022; Fahrion et al. 2019; Poci et al. 2019).
We construct triaxial Schwarzschild models for three mock late-type galaxies, created from the same simulation Auriga halo 6, but with inclination angles of 40°, 60° and 80°, respectively. The advantage of using mock galaxies is that we know the underlying true orbit distribution. The creation of the mock data and dynamical models were performed in the same setup described in Zhu et al. (2020), but using the triaxial Schwarzschild code version with correct and incorrect mirroring.
Figure 6 illustrates the stellar orbit distributions in radius r vs. circularity λz of the three mock galaxies derived by our models with the correct and incorrect mirroring. For each mock galaxy, we only use the best-fitting model. Their orbit distributions are compared to the true orbit distribution from the simulation. The darker colour indicates a higher phase space density. Being LTGs, the mock galaxies are dominated by a dynamical cold component (λz = 1) which is accompanied by a central hot component, the bulge of the galaxy. The proportion of cold and hot components is well reproduced for both the correct and incorrect mirroring. Differences caused by the incorrect mirroring are small compared to the systematic errors of the model (as inferred by departures from the ground truth), and independent of the inclination angle. The side panels in Fig. 6 confirm that the trends in the orbit fractions are almost the same for the correct and incorrect mirroring.
 |
Fig. 6. Stellar orbit distribution in intrinsic radius r vs. circularity |
Although the line-of-sight mean velocity (V) and velocity dispersion (σ) maps of each single orbit change with the incorrect mirroring in the code, we find that the orbit distributions in the r vs. λz plane of the best-fitting models do not noticeably change. This is because, as shown in Fig. 2, for each orbit larger differences in σ occur in the areas with low density. In areas with larger surface density (where orbit contributes more light to the model) the difference in σ is small. Our model is a combination of many orbits. For orbits with certain (V, σ) maps an alternative combination of orbits with similar (V, σ) maps might be found in the library calculated with the incorrect code version, although not orbits with exactly the same combination of integrals of motion (E, Lz, I3). When fitting to the kinematic maps, the two version of models may pick different orbits regarding to their E, Lz, I3, but prefer orbits with similar (V, σ), thus similar λz.
These results are not only true for the three mock galaxies. The stellar orbit distributions in the r vs. λz plane for all the galaxies we have remodelled using the correct mirroring in Sect. 3 are very similar to those obtained using the non-corrected code.
6. Conclusion and future work
Recently, Quenneville et al. (2022) reported a bug in the original triaxial Schwarzschild code published by van den Bosch et al. (2008) where some orbits had been incorrectly mirrored. After correcting the mirroring in our open-source triaxial Schwarzschild code (DYNAMITE, Jethwa et al. 2020), we carefully checked for systematic changes regarding the estimate of a black hole mass, enclosed mass, intrinsic shape and the stellar orbit distribution. We noticed small effects in the shape of the χ2 distribution, but the best-fit parameters with the correct and incorrect mirroring were in almost all cases consistent within their uncertainties. We did not see any noticeable trends with galaxy morphology, inclination angle or triaxiality.
den Brok et al. (2021) used the original triaxial Schwarzschild code to derive the black hole mass in PGC 046832 and found significant discrepancies between the results from the triaxial Schwarzschild code and axisymmetric dynamical methods. We have re-analysed the galaxy with the corrected triaxial Schwarzschild code, but obtained consistent results with den Brok et al. (2021).
We can therefore conclude that the incorrect mirroring did not systematically bias previous results obtained with the triaxial Schwarzschild code by van den Bosch et al. (2008).
Several other developments are planned for DYNAMITE in the near future. We will implement the orbit-colouring technique to incorporate stellar population information (Poci et al. 2019; Zhu et al. 2020) and offer more sophisticated parameter search algorithms (Gration & Wilkinson 2019). Finally, we recognise the need for a more thorough treatment of uncertainties for orbit-based modelling. An important step in this direction has been made in Lipka & Thomas (2021), who presented a novel technique to optimise the amount of regularization used for orbit-weight solving, which can have a significant impact on constraints on physical parameters such as galaxy mass. How to account for uncertainties on the orbit-weights themselves is an open question which has been largely ignored due to the difficulty of assigning meaningful uncertainties in the high-dimensional and degenerate space of orbit-weights, however, getting a handle on these uncertainties is vital if we wish to associate clumpiness in an orbit-distribution to the presence of merged galactic components. Addressing these concerns is the focus of our future research.
Acknowledgments
We thank M. Quenneville and their group for finding and reporting the bug in the original code. Their work has motivated us to re-evaluate previous results and report our work in this collaborative study. We also thank Eugene Vasiliev, the author of the SMILE orbit-superposition code, for many fruitful and constructive discussions. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 724857 (Consolidator Grant ArcheoDyn). The computational results presented have been achieved (in part) using the Vienna Scientific Cluster (VSC, https://vsc.ac.at). AP is supported by the Science and Technology Facilities Council through the Durham Astronomy Consolidated Grant 2020–2023 (ST/T000244/1).
References
- Ahn, C. P., Seth, A. C., Cappellari, M., et al. 2018, ApJ, 858, 102 [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [Google Scholar]
- Binney, J. 1982, ARA&A, 20, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Kawata, D., & Hunt, J. A. S. 2018, MNRAS, 473, 2288 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2020, MNRAS, 494, 4819 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Cretton, N., Rix, H.-W., & de Zeeuw, P. T. 2000, ApJ, 536, 319 [Google Scholar]
- Croom, S. M., Owers, M. S., Scott, N., et al. 2021, MNRAS, 505, 991 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Saglia, R. P., et al. 2008, MNRAS, 385, 1729 [Google Scholar]
- den Brok, M., Krajnović, D., Emsellem, E., Brinchmann, J., & Maseda, M. 2021, MNRAS, 508, 4786 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Fahrion, K., Lyubenova, M., van de Ven, G., et al. 2019, A&A, 628, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., & Martig, M. 2021, A&A, 646, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier-Krause, A., Zhu, L., Neumayer, N., et al. 2017, MNRAS, 466, 4040 [NASA ADS] [Google Scholar]
- Gebhardt, K., Richstone, D., Tremaine, S., et al. 2003, ApJ, 583, 92 [Google Scholar]
- Gebhardt, K., & Thomas, J. 2009, ApJ, 700, 1690 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. E., & Binney, J. J. 1996, MNRAS, 279, 993 [NASA ADS] [Google Scholar]
- Gration, A., & Wilkinson, M. I. 2019, MNRAS, 485, 4878 [NASA ADS] [CrossRef] [Google Scholar]
- Iodice, E., Sarzi, M., Bittner, A., et al. 2019, A&A, 627, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeans, J. H. 1922, MNRAS, 82, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Jethwa, P., Thater, S., Maindl, T., & Van de Ven, G. 2020, Astrophysics Source Code Library [record ascl:2011.007] [Google Scholar]
- Jin, Y., Zhu, L., Long, R. J., et al. 2020, MNRAS, 491, 1690 [NASA ADS] [Google Scholar]
- Krajnović, D., Cappellari, M., McDermid, R. M., et al. 2018, MNRAS, 477, 3030 [CrossRef] [Google Scholar]
- Krajnović, D., McDermid, R. M., Cappellari, M., & Davies, R. L. 2009, MNRAS, 399, 1839 [Google Scholar]
- Liepold, C. M., Quenneville, M. E., Ma, C.-P., et al. 2020, ApJ, 891, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lipka, M., & Thomas, J. 2021, MNRAS, 504, 4599 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [Google Scholar]
- Mehrgan, K., Thomas, J., Saglia, R., et al. 2019, ApJ, 887, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., & Fridman, T. 1996, ApJ, 460, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, R., & Miyamoto, M. 1976, PASJ, 28, 1 [NASA ADS] [Google Scholar]
- Neureiter, B., Thomas, J., Saglia, R., et al. 2021, MNRAS, 500, 1437 [Google Scholar]
- Pilawa, J. D., Liepold, C. M., Delgado Andrade, S. C., et al. 2022, ApJ, 928, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Poci, A., & Smith, R. J. 2022, MNRAS, 512, 5298 [NASA ADS] [CrossRef] [Google Scholar]
- Poci, A., Cappellari, M., & McDermid, R. M. 2017, MNRAS, 467, 1397 [NASA ADS] [Google Scholar]
- Poci, A., McDermid, R. M., Zhu, L., & van de Ven, G. 2019, MNRAS, 487, 3776 [Google Scholar]
- Poci, A., McDermid, R. M., Lyubenova, M., et al. 2021, A&A, 647, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, E. E., de Zeeuw, P. T., van der Marel, R. P., & Hunter, C. 1995, MNRAS, 274, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Quenneville, M. E., Liepold, C. M., & Ma, C.-P. 2022, ApJ, 926, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Richstone, D. O., & Tremaine, S. 1984, ApJ, 286, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., de Zeeuw, P. T., Cretton, N., van der Marel, R. P., & Carollo, C. M. 1997, ApJ, 488, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, C. A., Bentz, M. C., Vasiliev, E., Valluri, M., & Onken, C. A. 2021, ApJ, 916, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rusli, S. P., Thomas, J., Saglia, R. P., et al. 2013, AJ, 146, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B. 1987, in Structure and Dynamics of Elliptical Galaxies, ed. P. T. de Zeeuw, IAU Symp., 127, 397 [Google Scholar]
- Santucci, G., Brough, S., van de Sande, J., et al. 2022, ApJ, 930, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Iodice, E., Coccato, L., et al. 2018, A&A, 616, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Satoh, C. 1980, PASJ, 32, 41 [NASA ADS] [Google Scholar]
- Schwarzschild, M. 1979, ApJ, 232, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M. 1982, ApJ, 263, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, N., Cappellari, M., Davies, R. L., et al. 2013, MNRAS, 432, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Syer, D., & Tremaine, S. 1996, MNRAS, 282, 223 [Google Scholar]
- Thater, S., Krajnović, D., Bourne, M. A., et al. 2017, A&A, 597, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thater, S., Krajnović, D., Cappellari, M., et al. 2019, A&A, 625, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thater, S., Krajnović, D., Weilbacher, P. M., et al. 2022, MNRAS, 509, 5416 [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2007, MNRAS, 382, 657 [Google Scholar]
- Valluri, M., Merritt, D., & Emsellem, E. 2004, ApJ, 602, 66 [Google Scholar]
- van de Ven, G., de Zeeuw, P. T., & van den Bosch, R. C. E. 2008, MNRAS, 385, 614 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E. 2016, ApJ, 831, 134 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E., & de Zeeuw, P. T. 2010, MNRAS, 401, 1770 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E., van de Ven, G., Verolme, E. K., Cappellari, M., & de Zeeuw, P. T. 2008, MNRAS, 385, 647 [Google Scholar]
- van der Marel, R. P., Cretton, N., de Zeeuw, P. T., & Rix, H.-W. 1998, ApJ, 493, 613 [Google Scholar]
- Vasiliev, E., & Valluri, M. 2020, ApJ, 889, 39 [Google Scholar]
- Verolme, E. K., Cappellari, M., Copin, Y., et al. 2002, MNRAS, 335, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. L., van den Bosch, R. C. E., Barth, A. J., & Sarzi, M. 2012, ApJ, 753, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., van de Ven, G., Méndez-Abreu, J., & Obreja, A. 2018a, MNRAS, 479, 945 [Google Scholar]
- Zhu, L., van den Bosch, R., van de Ven, G., et al. 2018b, MNRAS, 473, 3000 [Google Scholar]
- Zhu, L., van de Ven, G., Leaman, R., et al. 2020, MNRAS, 496, 1579 [Google Scholar]
- Zhu, L., van de Ven, G., Leaman, R., et al. 2022, A&A, 664, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Impact of incorrect orbit mirroring for a model with close to axisymmetric potential
We consider here the effects of the correct and incorrect mirroring scheme for a galactic potential in the axisymmetric limit, derived from the luminosity model of the simulated Auriga galaxy halo 6 Zhu et al. (2020). Figures A.1 and A.2 show the impact of the incorrect orbit mirroring for a single orbit, in an analogous way to what is shown in Fig. 1 and 2 in Section 2.
To further explore the more complex triaxial case shown in Section 2, we show in Fig. A.3 and A.4 the impact of the mirroring on a long-axis tube orbit.
 |
Fig. A.1. Similar to Fig. 1 but for a short-axis tube orbit in a model with axisymmetric potential. The orbit is shown for 9 (out of 200) revolutions. The time of one orbital period is ∼0.44 Gyr. |
 |
Fig. A.2. Similar to Fig. 2 but for a short-axis tube orbit in a model with axisymmetric potential. This orbit has a large weight in the model that is discussed in section 5. |
 |
Fig. A.3. Similar to Fig. 1 but for an outer long-axis tube orbit in the model with triaxial potential. The orbit is shown for 40 (out of 200) revolutions. The time of one orbital period is ∼0.018 Gyr. |
 |
Fig. A.4. Similar to Fig. 2 but for an outer long-axis tube orbit in the model with triaxial potential. |
Appendix B: Stellar kinematic maps for a few example cases
In Figures B.1 and B.2, we show the kinematic maps obtained with DYNAMITE using the correct and incorrect orbit mirroring for a galaxy from each of the different surveys discussed in Section 3. It is clear that differences between the models with correct and incorrect mirroring are smaller than the differences between best-fit model and data.
 |
Fig. B.1. Kinematic maps for the SAMI galaxy 9403800123. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
 |
Fig. B.2. Kinematic maps for the ATLAS3D galaxy NGC 4365. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
 |
Fig. B.3. Kinematic maps for the Fornax3D galaxy FCC 179. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
Appendix C: Orbit distribution of PGC 046832
In Fig. C.1 we show the stellar orbit distribution obtained for the best-fit model of PGC 046832, when using a Schwarzschild code with correct orbit mirroring.
 |
Fig. C.1. Average orbital circularity of tube orbits as a function of radius for all models consistent with the best fit model of PGC 046832 (discussed in Section 4). Darker colours imply a higher density of orbits. The dashed lines separate hot orbits, warm orbits and cold orbits. |
All Tables
Quantitative comparison of derived parameters with correct and incorrect mirroring.
All Figures
 |
Fig. 1. Impact of the incorrect orbit mirroring for a single orbit. We show a typical short-axis tube orbit derived in the triaxial potential by den Brok et al. (2021). The four panels show the evolution of Ltot (top left), Lz (top right), Lx (bottom left) and Ly (bottom right). The original orbit, correct (‘bug-fix’) and incorrect (‘nofix’) mirrors are shown by gray, blue, and red colours, respectively. We only show the four mirroring cases (out of eight) that are changed compared to the original code (see Table 1). In one panel, rows from top to bottom represent the 2nd, 3rd, 6th, and 7th mirrors, respectively. We show the orbit for only 25 (out of 200) revolutions to avoid crowding. The time of one orbital period is ∼0.06 Gyr. |
| In the text | |
 |
Fig. 2. Impact of the incorrect orbit mirroring for a single orbit. We show a typical short-axis tube derived in the triaxial potential by den Brok et al. (2021). Columns from left to right show the orbit trajectories, the line-of-sight mean velocity V with the correct (‘bug-fix’) and incorrect mirroring (‘nofix’) and the relative error between the incorrect and correct mirroring schemes ΔV/V, the velocity dispersion σ with the correct (‘bug-fix’) and incorrect mirroring (‘nofix’) and the relative error. Rows from top to bottom refer to different inclination angles of 15°, 45° and 75°, respectively. The changes in the mean velocity and velocity dispersion are up to ∼40% in some regions of the orbit space, but they are usually ≲10% in regions where the star spends most of its life. |
| In the text | |
 |
Fig. 3. Comparison of enclosed mass properties of our galaxy samples separated in total mass within one effective radius Mtot(< Re) (left panel) and stellar mass-to-light ratio M*/L (right panel) for correct (‘bugfix’) and incorrect (‘nofix’) orbit mirroring. The galaxy sample is a subset of Fornax3D LTGs and ETGs (green squares), SAMI passive galaxies (purple stars) and ATLAS3D ETGs (orange circles). Also added as black diamonds are the massive lensed ETG ESO286-G022 by Poci & Smith (2022), FCC 47 by Fahrion et al. (2019) and Thater et al. (in prep.), PGC 046832 by den Brok et al. (2021), which is also discussed in Sect. 4, and the three simulated LTGs by Zhu et al. (2020), which are discussed in Sect. 5. The dashed line shows the 1-1 line between the different versions. Both the derived total and stellar mass are not significantly affected by the incorrect mirroring of the orbits. Differences between the versions are within the reported statistical uncertainties of the dynamical modelling. Uncertainties were calculated by including all models within |
| In the text | |
 |
Fig. 4. Comparison of inferred galaxy intrinsic shape parameters for our modelled galaxies. The galaxy sample is divided into Fornax3D LTGs and ETGs (squares), SAMI passive galaxies (stars) and ATLAS3D ETGs (circles). Also added as diamonds are the massive lensed ETG ESO286-G022 by Poci & Smith (2022), FCC 47 by Fahrion et al. (2019) and Thater et al. (in prep.), PGC 046832 by den Brok et al. (2021), which is also discussed in Sect. 4, and the three simulated LTGs by Zhu et al. (2020), which are discussed in Sect. 5. Both the intrinsic intermediate-to-major axis ratio p (left panel) and minor-to-major axis ratio q (right panel) show no significant change for the majority of the galaxies. There is no clear trend of increasing discrepancy with galaxy morphology or triaxiality T ≡ (1 − p2)/(1 − q2). Uncertainties were calculated by including all models within |
| In the text | |
 |
Fig. 5. Contours describing the χ2 surfaces at different black hole masses MBH and mass to light ratios M/L. Red contours show the χ2 surface using the original version of the Schwarzschild code, and were previously presented in den Brok et al. (2021). Blue contours show the χ2 surface after correcting the mirroring bug in the code. Grey dots show the locations at which models were calculated. The thick contours contain models within |
| In the text | |
 |
Fig. 6. Stellar orbit distribution in intrinsic radius r vs. circularity |
| In the text | |
 |
Fig. A.1. Similar to Fig. 1 but for a short-axis tube orbit in a model with axisymmetric potential. The orbit is shown for 9 (out of 200) revolutions. The time of one orbital period is ∼0.44 Gyr. |
| In the text | |
 |
Fig. A.2. Similar to Fig. 2 but for a short-axis tube orbit in a model with axisymmetric potential. This orbit has a large weight in the model that is discussed in section 5. |
| In the text | |
 |
Fig. A.3. Similar to Fig. 1 but for an outer long-axis tube orbit in the model with triaxial potential. The orbit is shown for 40 (out of 200) revolutions. The time of one orbital period is ∼0.018 Gyr. |
| In the text | |
 |
Fig. A.4. Similar to Fig. 2 but for an outer long-axis tube orbit in the model with triaxial potential. |
| In the text | |
 |
Fig. B.1. Kinematic maps for the SAMI galaxy 9403800123. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
| In the text | |
 |
Fig. B.2. Kinematic maps for the ATLAS3D galaxy NGC 4365. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
| In the text | |
 |
Fig. B.3. Kinematic maps for the Fornax3D galaxy FCC 179. From left to right the columns show the flux, velocity, velocity dispersions and h3 and h4 Gauss-Hermite moments. From top to bottom the rows show the original data, the DYNAMITE model with correct mirroring, the DYNAMITE model with incorrect mirroring, the residuals between data and the correct DYNAMITE model divided by the kinematic uncertainties, and the relative difference between the models with correct and incorrect mirroring divided by the kinematic uncertainties. |
| In the text | |
 |
Fig. C.1. Average orbital circularity of tube orbits as a function of radius for all models consistent with the best fit model of PGC 046832 (discussed in Section 4). Darker colours imply a higher density of orbits. The dashed lines separate hot orbits, warm orbits and cold orbits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.