| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202348335 | |
| Published online | 05 April 2024 | |
Fast computation of the observer motion effects induced on monopole frequency spectra for tabulated functions
1
INAF, Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
e-mail: [email protected]
2
INFN, Sezione di Bologna, Via Irnerio 46, 40127 Bologna, Italy
3
Department of Astronomy, University of Geneva, Ch. d’Écogia 16, 1290 Versoix, Switzerland
4
Departamento de Física Universidad de Oviedo, C. Federico García Lorca 18, 33007 Oviedo, Spain
5
Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), C. Independencia 13, 33004 Oviedo, Spain
Received:
20
October
2023
Accepted:
9
January
2024
Context. Various methods have been studied to compute the boosting effects produced by the observer peculiar motion, which modifies and transfers the isotropic monopole frequency spectrum of the cosmic background radiation to higher multipoles. Explicit analytical solutions for the spherical harmonic expansion coefficients were already presented and applied to different types of background spectrum, strongly alleviating the computational effort needed for accurate theoretical predictions. The frequency spectra at higher multipoles are inherently led by higher-order derivatives of the monopole spectrum. Provided that it can be well described by analytic or semi-analytic functions, the computation of its transfer is not affected by numerical instabilities when evaluated at the required level of numerical accuracy. Instead, monopole frequency spectra described by tabulated functions are computed with a relatively poor frequency resolution in comparison with the Doppler shift, which necessitates interpolation of the tabular representation. The spectra are also affected by uncertainties related to intrinsic inaccuracies in the modelling or in the related observational data as well as to limited accuracy in their numerical computation. These uncertainties propagate and increase with the derivative order, possibly preventing the trustworthy computation of the transfer to higher multipoles and of the observed monopole.
Aims. We study methods to filter the original function or its derivatives and the multipole spectra, to mitigate numerical instabilities, and to derive reliable predictions of the harmonic coefficients for different cosmic background models.
Methods. From the analytical solutions, and assuming that the monopole spectrum can be expanded in Taylor’s series, we derive explicit expressions for the harmonic coefficients up to the multipole ℓmax = 6 in terms of monopole spectrum derivatives. We then consider different low-pass filters: prefiltering in Fourier space of the tabular representation; filtering in both real and Fourier space of the numerical derivatives; interpolation approaches; and a dedicated method based on amplification and deamplification of the boosted signal. We study the quality of these methods when applied to suitable analytical approximations of the tabulated functions, possibly polluted with simulated noise. These methods are then applied to the tabulations.
Results. We consider two very different types of monopole spectra superimposed to the cosmic microwave background: the (smooth) extragalactic source microwave background signal from radio-loud active galactic nuclei and the (feature-rich) redshifted 21 cm line, and present our results in terms of spherical harmonic coefficients. The direct prediction of these coefficients can be noisy at ℓ > 1 or, depending on the uncertainty level, even at ℓ ≤ 1. Without assuming a functional form for the extragalactic background spectrum, the Gaussian prefiltering coupled to the sequential real-space filtering of derivatives allows us to derive accurate predictions up to ℓ ∼ 6, while a log–log polynomial representation, which is appropriate over several decades, gives accurate solutions at any ℓ. Instead, it is difficult to characterise the 21 cm line model variety, and so it is relevant to work without assumptions about the underlying function. Typically, the prefiltering provides accurate predictions up to ℓ ≃ 3 or 4, while the further sequential filtering of the derivatives or the boosting amplification and deamplification method improves the results up to ℓ = 4, while also allowing reasonable estimations of the spectrum at higher ℓ.
Conclusions. The proposed methods can significantly extend the range of realistic cosmic background models manageable with a fast computation, beyond the cases characterised a priori by analytical or semi-analytical functions. These methods require only an affordable increase in computation time compared to the direct calculation via simple interpolation.
Key words: cosmic background radiation / diffuse radiation / methods: analytical
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The observer peculiar motion with respect to the cosmic background radiation produces boosting effects that modify the isotropic monopole frequency spectrum of the background and transfer it to higher multipoles. The monopole spectrum can therefore be investigated through the frequency dependence of the signal variation in the sky. Various methods have been studied to compute these effects for different kinds of background signals and to explore the perspectives of such differential approaches in various observational frameworks (e.g., Danese & De Zotti 1981; Balashev et al. 2015; De Zotti et al. 2016; Slosar 2017; Burigana et al. 2018; Mukherjee et al. 2018; Deshpande 2018; Trombetti & Burigana 2019).
The use of the dipole spectrum as an additional probe of the background monopole spectrum was proposed more than 40 years ago, but this approach has only recently been deeply investigated in the context of future experiments as a way to circumvent difficulties in absolute calibration and to deal with the foreground impact that could be less relevant in dipole than in monopole analyses. The need for relative and inter-frequency calibration, which are common to both absolute and differential approaches – although in principle less critical than in the latter –, represents a key aspect. In the context of future cosmic microwave background (CMB) missions, which include the detection and characterisation of spectral distortions in their scientific aims, the impact in dipole analyses of potential residuals from imperfect calibration and the conceptual design of instrument and measurement techniques for the final output calibration have already been addressed in Burigana et al. (2018) and in Mukherjee et al. (2018), respectively.
The transfer of the isotropic monopole spectrum to multipole spectra beyond the dipole or quadrupole could be the subject of future dedicated observational studies. We focus here on the fast computation of the coefficients of the spherical harmonic expansion for generic background functions.
Analytical solutions of a system of linear equations to explicitly compute the terms of spherical harmonic expansion were recently presented and applied to different types of background spectrum and their combinations, significantly alleviating the computational effort needed for accurate theoretical predictions, including high-order contributions (Trombetti et al. 2021). The frequency spectra at higher multipoles are inherently led by higher-order derivatives of the monopole frequency spectrum. Provided it can be exhaustively described by analytic or semi-analytic functions and the calculation is performed at the required level of numerical accuracy, the computation of the frequency spectra at higher multipoles is not affected by numerical instabilities. The situation is very different for monopole frequency spectra described by tabulated functions. These are typically computed with a relatively poor resolution in frequency, ν, in comparison with the order of the Doppler shift in frequency, δν/ν ∼ β = v/c, where v and c are the speed of the observer and that of light, respectively, and therefore interpolation of the tabular representation is required. Furthermore, these spectra are affected by uncertainties related to intrinsic inaccuracies in astrophysical modelling or in related ingested observations or to limited accuracy in their numerical computation. These inaccuracies propagate and increase with the derivative order, possibly causing significant instabilities. According to the quality of the tabulated monopole frequency spectrum, these inaccuracies and instabilities may in principle prevent a robust and accurate computation of its transfer to higher multipoles or even at ℓ ≤ 1. The scope of this paper is to identify approaches that can be applied to derive reliable predictions of the harmonic coefficients for a wide range of background models.
In Sect. 2, we introduce the adopted formalism. Starting from the analytical solutions for the spherical harmonic coefficients and assuming that the monopole frequency spectrum can be expanded in Taylor’s series, we derive explicit expressions for the spherical harmonic coefficients in terms of monopole frequency spectrum derivatives and discuss their scaling relations, which are relevant for the subsequent sections. Among the plethora of possible background models, we focus on two classes of monopole spectra (Sect. 3) usually represented by tabulated functions, namely the (smooth) extragalactic sources microwave background (ESMB) signal from radio-loud active galactic nuclei (AGN) and the (feature-rich) redshifted 21 cm line, both of which are superimposed to the CMB spectrum. These two classes of models are very different in the size of the frequency range in which they are relevant and in the spectral shape, thus offering the possibility to test the developed methods under very different conditions. In Sect. 4, we show the type of inaccuracy and instability appearing in the computation of the transfer of the monopole frequency spectrum to the higher multipoles when applying the analytical solutions directly. We study the effects of these approaches to frequency spectra at different multipoles by first considering suitable analytical approximations of the tabular representations, which can be polluted with simulated noise in the range of the quoted uncertainties of the models, and then tabulated functions. The results are presented in terms of spherical harmonic coefficients. In Sect. 5.2, we discuss methods to filter the original tabulated function or its derivatives and, ultimately, the higher multipole spectra to mitigate numerical instability. We consider different filters, from prefiltering in Fourier space of the original tabulated background function to filtering in both real and Fourier space of the numerical derivatives, from local and, where feasible, global interpolation approaches to a dedicated method of amplification and deamplification of the boosting. The above methods are applied to the two considered classes of monopole spectra in Sect. 6, where we present our main results. Section 7 provides a comparison among the results found for the different filtering methods applied to these classes of monopole spectra, some guidelines to help in identification of the best types of treatments, a discussion of the required computational time, and our main conclusions.
2. Theoretical framework
The Compton-Getting effect (Forman 1970), based on the Lorentz invariance of the photon distribution function, η(ν), allows us to describe how the peculiar velocity of an observer impacts the frequency spectrum on the whole sky. At the frequency ν, the observed signal in equivalent thermodynamic temperature, Tth(ν) = (hν/k)/ln(1 + 1/η(ν)), is
where
with
In the above formulas,  is the sky direction unit vector, β = v/c is the observer velocity, x = hν/(kTr) is the CMB redshift invariant dimensionless frequency, Tr = T0(1 + z) is the CMB redshift dependent effective temperature, k and h are the Boltzmann and Planck constants, and the notation “BB/dist” indicates a blackbody spectrum or any type of spectral distortion (Burigana et al. 2018). Here, T0 is the current CMB effective temperature in the blackbody spectrum approximation such that
is the sky direction unit vector, β = v/c is the observer velocity, x = hν/(kTr) is the CMB redshift invariant dimensionless frequency, Tr = T0(1 + z) is the CMB redshift dependent effective temperature, k and h are the Boltzmann and Planck constants, and the notation “BB/dist” indicates a blackbody spectrum or any type of spectral distortion (Burigana et al. 2018). Here, T0 is the current CMB effective temperature in the blackbody spectrum approximation such that  gives the current CMB energy density with a = 8πI3k4/(hc)3, I3 = π4/15. From the joint analysis of the data from the Far Infrared Absolute Spectrophotometer (FIRAS) on board the Cosmic Background Explorer (COBE) and from the Wilkinson Microwave Anisotropy Probe (WMAP), Fixsen (2009) derived T0 = (2.72548 ± 0.00057) K.
gives the current CMB energy density with a = 8πI3k4/(hc)3, I3 = π4/15. From the joint analysis of the data from the Far Infrared Absolute Spectrophotometer (FIRAS) on board the Cosmic Background Explorer (COBE) and from the Wilkinson Microwave Anisotropy Probe (WMAP), Fixsen (2009) derived T0 = (2.72548 ± 0.00057) K.
Expanding Eq. (1) in spherical harmonics coefficients gives
To simplify the problem, we chose a reference system such as to maintain the dependence on the colatitude θ and to make the dependence on the longitude ϕ vanish; that is, with the z axis parallel to the observer velocity. This means that only the coefficients aℓ, m(ν, β) with m = 0 do not vanish. The aℓ, 0(ν, β) amplitude decreases as βℓ ⋅ p at increasing multipole, ℓ, with p ≈ 1 (for a BB, p = 1 and aℓ, 0(ν, β) = aℓ, 0(β)).
2.1. Structure of analytical solutions
Fixing ℓmax to a specific value in Eq. (4), it is possible to identify a system of linear equations in the N unknowns aℓ, 0(ν, β), where N = ℓmax + 1 is the number of sky directions, evaluating the signal  through Eq. (1). From Planck Collaboration I (2020) we know that β = (1.2336 ± 0.0004) × 10−3, and therefore choosing ℓmax = 6 provides a high numerical accuracy1. Moreover, the associated Legendre polynomials are characterised by a symmetry property with respect to π/2, and therefore a suitable choice of the N colatitudes θi allows us to divide the system into two subsystems, one for ℓ = 0 and even multipoles and the other for odd multipoles. The advantage of this separation is that it improves the accuracy of the solution because neglecting higher ℓ produces an error that mainly arises from the terms at ℓmax + 2 for even ℓ (or at ℓmax + 1 for odd ℓ; Trombetti et al. 2021). The same consideration holds for different ℓmax.
through Eq. (1). From Planck Collaboration I (2020) we know that β = (1.2336 ± 0.0004) × 10−3, and therefore choosing ℓmax = 6 provides a high numerical accuracy1. Moreover, the associated Legendre polynomials are characterised by a symmetry property with respect to π/2, and therefore a suitable choice of the N colatitudes θi allows us to divide the system into two subsystems, one for ℓ = 0 and even multipoles and the other for odd multipoles. The advantage of this separation is that it improves the accuracy of the solution because neglecting higher ℓ produces an error that mainly arises from the terms at ℓmax + 2 for even ℓ (or at ℓmax + 1 for odd ℓ; Trombetti et al. 2021). The same consideration holds for different ℓmax.
Using the methods of elimination and substitution, the two subsystems can be easily solved. In particular, independently of the background spectral type, the aℓ, m(ν, β) solution is given by a linear combination of the sums and differences of the signals from Eq. (1) evaluated at a θi that is symmetrical with respect to π/2 (Trombetti et al. 2021; Burigana et al. 2022).
For ℓmax = 6 and selecting θi = 0, π/4, π/3, π/2, (2/3)π, (3/4)π, and π (or the corresponding  ) in order to simplify the algebra, we have
) in order to simplify the algebra, we have
for ℓ = 0 and even multipoles, and
for odd multipoles. For the assumed θi, Table 1 gives the coefficients Aℓ and dℓ, i (Trombetti et al. 2021).
Aℓ and dℓ, i coefficients.
2.2. Taylor’s series expansion: Harmonic coefficients and derivatives
The solutions described by Eqs. (5) and (6) have a structure that shows some similarities with the weights for the centred approximation numerical derivative scheme (Fornberg 1988), as already discussed in Trombetti et al. (2021). This indicates that there is a close relationship with the derivatives of the considered signal, as underlined for the first time in Danese & De Zotti (1981) for the dipole.
We note that the values of  should always be very close to the value computed at w = 0; that is, in the direction perpendicular to the observer motion. Let us assume that
should always be very close to the value computed at w = 0; that is, in the direction perpendicular to the observer motion. Let us assume that  can be expanded in Taylor’s series around w = 0. Adopting the Lagrange notation, we use
can be expanded in Taylor’s series around w = 0. Adopting the Lagrange notation, we use  ,
,  , ...,
, ...,  to denote the derivatives of
to denote the derivatives of  performed with respect to w evaluated at w = 0, from order zero2 to order six. Given the adopted set of wi, after some calculations, Eqs. (5) and (6) can be rewritten as
performed with respect to w evaluated at w = 0, from order zero2 to order six. Given the adopted set of wi, after some calculations, Eqs. (5) and (6) can be rewritten as
for ℓ = 0 and even multipoles, and
for odd multipoles. Equations (7) and (8) show that only the derivatives of even (odd) order contribute to aℓ, 0 for even (odd) ℓ. This is a consequence of the separation of the system into two subsystems, one for ℓ = 0 and even multipoles and the other for odd multipoles.
Finally, inserting the values of the Aℓ and dℓ, i coefficients, after some algebra, we have
where each denominator, Dℓ, in front of the square root can be rewritten as Dℓ = (2ℓ−1)Dℓ − 1, with D0 = 1. Equations (9)–(15) show that only the derivatives of order equal to or greater than ℓ contribute to aℓ, 0 and that the multiplicative factor in front of each derivative strongly decreases with the order of the derivative. We note that this property and the typical overall scaling of aℓ, 0(ν, β), which is almost proportional to βℓ ⋅ p mentioned in Sect. 2, do not imply that at each multipole ℓ the terms from the derivatives of order greater than ℓ are in general not relevant, because it is necessary to take into account the different frequency dependencies of the derivatives of different orders (we develop this point after introducing background signals and other basic concepts; see Appendix E).
2.3. Scaling of derivatives
In the previous section, we formally derive the link between the aℓ, 0 coefficients and the derivatives of  with respect to w evaluated at w = 0. Here, we discuss the relationship between the derivatives performed with respect to w and the ones performed with respect to the frequency, and their scaling relations, which are relevant in following sections.
with respect to w evaluated at w = 0. Here, we discuss the relationship between the derivatives performed with respect to w and the ones performed with respect to the frequency, and their scaling relations, which are relevant in following sections.
From Eq. (1), considering that ν′=ν(1 − βw)/(1 − β2)1/2 and omitting the suffix “BB/dist” for simplicity, in the Leibniz notation we have
for the first derivative, and
for the second one.
In general, as the factor −βν/(1 − β2)1/2 does not contain w, for the subsequent nth derivatives we have
From Eqs. (16)–(18), the derivatives  in Sect. 2.2, evaluated at w = 0, can be rewritten setting
in Sect. 2.2, evaluated at w = 0, can be rewritten setting
where  is estimated at w = 0 (or θ = π/2):
is estimated at w = 0 (or θ = π/2):
Considering a speed, βa, different from β, the ratio between the derivatives  computed for these two different speeds is
computed for these two different speeds is
where fa = βa/β and
with  defined as in Eq. (20) but for β = βa.
defined as in Eq. (20) but for β = βa.
For β and βa significantly less than unity,  . All the three factors on the right hand side of Eq. (21) are in principle different from unity. On the other hand, except for possible functions Tth with extreme variation in frequency,
. All the three factors on the right hand side of Eq. (21) are in principle different from unity. On the other hand, except for possible functions Tth with extreme variation in frequency,  is the only term that can be significantly different from unity. We note that the extremely accurate computation of Rn, that is, of its very little difference from unity, would require analogous knowledge of the change of the corresponding order derivative in an extremely narrow range between
is the only term that can be significantly different from unity. We note that the extremely accurate computation of Rn, that is, of its very little difference from unity, would require analogous knowledge of the change of the corresponding order derivative in an extremely narrow range between  and
and  , which is the missing information in the problem under consideration, calling for the methods studied in this work. In practice, we set Rn = 1. Of course, this limitation, the treatment of which is out of the scope of this work, is much less critical than the instability problem object of this work3.
, which is the missing information in the problem under consideration, calling for the methods studied in this work. In practice, we set Rn = 1. Of course, this limitation, the treatment of which is out of the scope of this work, is much less critical than the instability problem object of this work3.
3. Monopole spectrum tabulated models
3.1. ESMB: Smooth spectral shape
Extragalactic radio and microwave sky, from hundreds of MHz to a few hundred GHz, is dominated by sources powered by AGN, in which the observed flux density is produced by synchrotron radiation generated by the acceleration of relativistic charged particles. The frequency spectra of radio AGN, generally characterised by a power law (S ∝ να) with a steep (α < −0.5) or flat (−0.5 < α < 0.5) slope depending on observed fluxes, mainly originate from extended (optically thin) radio lobes or from compact (optically thick) regions of the radio jet, respectively. In the “unified model” (e.g., Urry & Padovani 1995; Netzer 2015), these two populations arise from the different orientation of the observer relative to the axis of the characteristic jets emerging from the central black hole: in the case of a side-on view of the jet axis, the observed (low-frequency) emission emerges from the extended lobes, with a typically steep spectrum. On the other hand, if the line of sight is close to the axis of the emitting jet, objects appear as compact flat-spectrum sources, and are referred to as blazars (e.g., De Zotti et al. 2010). Due to orientation effects, steep-spectrum sources are much more often observed than blazars and therefore are the most relevant population at classical radio frequencies, that is, below 10 − 20 GHz. However, because of the spectral behaviour, their relevance reduces increasingly with frequency and they become subdominant with respect to flat-spectrum sources starting from a few tens of GHz.
Number counts of extragalactic radio sources are well determined at radio frequencies ν ≲ 10 GHz down to flux densities of S ≪ 1 mJy thanks to deep and large-area surveys (e.g., De Zotti et al. 2010; Bonavera et al. 2011; Massardi et al. 2011; Condon et al. 2012; Miller et al. 2013; Smolčić et al. 2017; Huynh et al. 2020). Luminosity functions and multi-frequency number counts of radio sources are also well modelled at these frequencies (e.g., Toffolatti et al. 1998; De Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011; Tucci & Toffolatti 2021). Very recently, Tompkins et al. (2023) published a thorough discussion of source number counts at centimetre wavelengths, showing that the AGN population dominates the number counts down to flux densities of S ≳ 1 mJy. At higher frequencies, that is, from tens of GHz to millimetre wavelengths, observational data on radio sources are mainly provided by CMB experiments (e.g., Planck Collaboration XXVI 2016; Datta et al. 2019; Gralla et al. 2020; Everett et al. 2020), which are able to detect only bright sources, down to tens of mJy at best. The uncertainties on number counts are still large, especially in the frequency range where the CMB dominates, that is, between 70 and 300 GHz.
In this analysis, we use the differential number counts, nν(S), of extragalactic radio sources at radio/microwave frequencies provided by the Tucci et al. (2011) model, in its updated version (Lagache et al. 2020) based on recent data from the Atacama Cosmology Telescope (ACT; Datta et al. 2019) and South Pole Telescope (SPT; Everett et al. 2020) experiments. Similarly to the evolutionary model of De Zotti et al. (2005), radio sources in the NRAO VLA Sky Survey (NVSS) and Green Bank 6-cm (GB6) surveys (Gregory et al. 1996; Condon et al. 1998) are separated into steep- and flat-spectrum sources according to their spectral behaviour measured between 1 and 5 GHz. Flux densities of radio sources are then extrapolated to higher frequencies by considering the characteristics of the physical mechanisms of emission (Blandford & Königl 1979; Konigl 1981) for the different source populations identified (as opposed to the approach of De Zotti et al. (2005), who apply a simple power-law extrapolation of radio spectra to higher frequencies). In particular, in the Tucci et al. (2011) model, the spectrum of flat-spectrum sources is expected to break at some frequency in the range of 10 − 1000 GHz and to steepen at higher frequencies due to electron-cooling effects and to the transition of the observed synchrotron emission from the optically thick to the optically thin regime. The frequency break is different for flat-spectrum radio quasars (FSRQs) and for BL Lac objects. In the former population, the spectral break is expected to typically occur at ν < 100 GHz, while in BL Lacs it should appear at ν ≳ 100 GHz (implying more compact emitting regions than those of FSRQs). The Tucci et al. (2011) model4, and its update published in Lagache et al. (2020), provides a good fit of observational number counts from all the CMB experiments at frequencies between 30 and 220 GHz down to flux densities of 10 mJy or less. Moreover, as discussed by Massardi et al. (2022), the “C2Ex” model is also able to give a very good fit to the very recent number counts calculated from a complete sample of blazars selected by the Herschel Astrophysical Terahertz Large Area Survey (H-ATLAS). The model also appears to be in good agreement with the “extragalactic radio background light” at GHz frequencies estimated by Tompkins et al. (2023), as defined there, calculated without excluding the brightest discrete extragalactic sources, that is, without a high flux density limit: the model finds 105, 10.6, 2.4, and 0.57 mK at 1.4, 3, 5, and 8.4 GHz, respectively, very close to the values reported by Tompkins et al. (2023) in their third column of their Table 6B labelled “AGN-fit EBL”.
Based on the modelled differential number counts we estimate the extragalactic background intensity between 1 GHz and 1 THz5, in a grid of 512 frequencies equally spaced in logarithmic units. The background intensity, I(ν) = (2h/c2) ν3 η(ν) = (2k/c2) ν2 Tant(ν), where Tant(ν) = (hν/k) η(ν) is the corresponding antenna temperature, and is proportional to  , where Smax corresponds to the detection threshold above which sources are detected and removed from the data, while Smin is the minimum flux density considered (sources with flux densities below this value should add a negligible contribution to the above integral). The background intensity is shown in Fig. 1 for five values of Smax, from 0.01 to 0.1 Jy. The largest value corresponds (approximately) to the detection limit of all-sky experiments, such as Planck, while the smallest corresponds to the limit of high-resolution CMB experiments, such as SPT and ACT. On the other hand, number counts are modelled down to Smin ∼ 10 μJy. Below this value, the contribution of classical extragalactic radio sources (that is, mainly steep-spectrum giant ellipticals and quasars (QSOs)) is not expected to be completely negligible. For example, Tucci & Toffolatti (2021) modelled luminosity functions of radio-loud AGN at GHz frequencies and provided estimates of number counts at 1 − 15 GHz down to 1 μJy. Based on those results, we find that changing Smin from 10 to 1 μJy increases the background intensity estimates by a few per cent, within the range of the considered Smax. Although the missing contribution can be larger at microwave wavelengths, our estimates of the background intensity should be a good approximation of the true value, and the choice of minimum flux Smin = 10 μJy should not affect the conclusions of the present analysis. We note the change in slope of the extragalactic background at 10 − 50 GHz in Fig. 1: at higher frequencies the frequency spectrum flattens due to the fact that blazars become increasingly dominant over steep-spectrum extragalactic sources.
, where Smax corresponds to the detection threshold above which sources are detected and removed from the data, while Smin is the minimum flux density considered (sources with flux densities below this value should add a negligible contribution to the above integral). The background intensity is shown in Fig. 1 for five values of Smax, from 0.01 to 0.1 Jy. The largest value corresponds (approximately) to the detection limit of all-sky experiments, such as Planck, while the smallest corresponds to the limit of high-resolution CMB experiments, such as SPT and ACT. On the other hand, number counts are modelled down to Smin ∼ 10 μJy. Below this value, the contribution of classical extragalactic radio sources (that is, mainly steep-spectrum giant ellipticals and quasars (QSOs)) is not expected to be completely negligible. For example, Tucci & Toffolatti (2021) modelled luminosity functions of radio-loud AGN at GHz frequencies and provided estimates of number counts at 1 − 15 GHz down to 1 μJy. Based on those results, we find that changing Smin from 10 to 1 μJy increases the background intensity estimates by a few per cent, within the range of the considered Smax. Although the missing contribution can be larger at microwave wavelengths, our estimates of the background intensity should be a good approximation of the true value, and the choice of minimum flux Smin = 10 μJy should not affect the conclusions of the present analysis. We note the change in slope of the extragalactic background at 10 − 50 GHz in Fig. 1: at higher frequencies the frequency spectrum flattens due to the fact that blazars become increasingly dominant over steep-spectrum extragalactic sources.
 |
Fig. 1. Comparison among the tabulated intensities of the considered ESMB model (C2Ex) for the different detection thresholds Smax discussed in the main text. See legend for an explanation of the symbols and lines. |
In order to obtain a reference analytical representation of the ESMB intensity, we fitted log I(ν) as a function of log ν with polynomials of different degrees6. For these five detection thresholds, we found that a nine-degree polynomial – with coefficients appropriate to each case – fits the tabulated ESMB intensity very well: as shown in Fig. 2 for the maximum and minimum values of Smax, the relative difference between the fitting polynomial and the original tabulation is found to be between ∼10−4 and ∼10−3. This range of values can be assumed as a reasonable estimate of the relative uncertainty of the functional representation of the ESMB. The statistical errors due to the different sample sizes of extragalactic sources that are used to estimate their number counts are instead much larger (typically ≳5 − 10%)7.
 |
Fig. 2. Absolute value of the difference between the log–log polynomial interpolations and the original tabulations (bottom curves) for the maximum and minimum detection thresholds adopted in the calculation of the ESMB total intensity (top curves). See legend for an explanation of the symbols and lines. |
3.2. Redshifted 21 cm line: Feature-rich spectral shape
The 21 cm line corresponds to the spin–flip transition in the ground state of neutral hydrogen (HI). This signal is described as the offset of the 21 cm brightness (that is, antenna) temperature from the background temperature, Tback, along the observed line of sight at a frequency ν that, because of cosmic expansion, is related to the rest frame frequency, ν21 cm = c/(21 cm), by ν = ν21 cm/(1 + z). Tback is usually assumed equal to Tr but in general it could include potential distortions and other radiation backgrounds. As the signal detected at a given frequency corresponds to a specific redshift, the 21 cm line provides a tomographic view of the cosmic evolution.
A rich set of redshifted 21 cm line models is presented in Cohen et al. (2017), resulting in a wide range of predictions for the antenna temperature. From a large dataset of standard astrophysical models, the publicly available 21 cm Global EMulator code8 (21cmGEM) predicts the global 21 cm signal over the redshift interval between 5 and 50 including both the epoch of reionisation (EoR) and cosmic dawn. Each model corresponds to a specific row number (#r) in the dataset and is based on seven key astrophysical parameters: the star formation efficiency (f*), the minimum virial circular velocity of star-forming haloes (Vc), the X-ray radiation efficiency (fX), the CMB optical depth (τ), the slope (α) and minimum energy (υmin) of the X-rays spectral energy distribution (SED) and the ionizing efficiency of sources (Rmfp) (Cohen et al. 2020). From a total of 2186 test models computed with the 21cmGEM code, we extract six scenarios that cover a sufficiently wide range of different shapes and signals. The names, row numbers and key parameters of these models are reported in Table 2.
Model name, its corresponding row number and the seven key parameters for the 21 cm signals from the 21cmGEM code.
Detecting and characterising the redshifted 21 cm line from the diffuse HI in the intergalactic medium is experimentally very challenging and requires an extremely accurate subtraction of the much more intense foreground signals. A pronounced absorption profile centred at (78 ± 1) MHz has been found by Bowman et al. (2018) based on the data from the Experiment to Detect the Global EoR Signature (EDGES). The authors described the absorption profile in terms of a flattened Gaussian identified by a set of best-fit parameters9. This representation, being fully analytical, is adopted as a reference model to test the quality of the methods examined in the present paper.
In Fig. 3, we show the extracted simulated models and the anomalously strong and narrow absorption feature of EDGES, the latter displayed in the inset because of its more pronounced temperature decrement with respect to the others.
 |
Fig. 3. Comparison between the considered redshifted 21 cm line models. See legend and text. |
The 21 cm signals are produced in an equally spaced redshift grid of 451 points with a 0.1 step from z = 50 to z = 5, that is, in a frequency range between ∼27.85 GHz and ∼236.73 GHz. The B, C and E models are characterised by a temperature decrement that becomes positive above a certain frequency, which is different from the other scenarios and from the EDGES profile. We adopt the same grid to also produce the tabulation based on the EDGES analytical representation.
4. Instability of harmonic coefficients with direct formulas
Here, we present the results of the computation of the transfer of the monopole frequency spectrum to the higher multipoles, directly applying the analytical solutions given in Sects. 2.1–2.3.
As in Trombetti et al. (2021), we show our results in terms of spherical harmonic coefficients aℓ, 0(ν, β) from ℓ = 1 to ℓmax = 6 but expressed in terms of their difference, Δaℓ, 0, from the coefficients aℓ, 0(ν, β)BB obtained in the case of a monopole frequency spectrum represented by a blackbody at the temperature T0. Particularly for low signals, the relevant information is indeed contained in the differences of the aℓ, 0(ν, β) coefficients with respect to the ones corresponding to a suitable reference case. Typically, the observer velocity is assumed to be the same with respect to a frame at rest with the CMB or other extragalactic backgrounds. The scaling with β (see Sect. 2.3) of the aℓ, 0(ν, β) coefficients for the CMB and the backgrounds is the same, and therefore Δaℓ, 0 scale accordingly10.
For the redshifted 21 cm line, as a reference case in the calculation of the difference Δaℓ, 0, one could also consider, for comparison, the combined signal of a BB at the temperature T0 plus a suitable representation of the radio extragalactic background spectrum, which indeed dominates over the standard CMB BB spectrum at ν ≲ 1 GHz (see e.g. Appendix A in Baiesi et al. 2020 for a recent data compilation).
Although we mainly focus on ℓ ≥ 1, in the following sections we also consider results regarding the ratio,  , between the equivalent thermodynamic temperature of observed and intrinsic monopole, expressing it in terms of the difference (Trombetti et al. 2021) ΔR = R − RBB, where, theoretically, RBB ≃ (1 − 2.5362 × 10−7) is the same ratio but for the case of the blackbody at the present temperature T0. Indeed, as explicitly shown by Eq. (9), the contribution from high-order derivatives appears also in a0, 0.
, between the equivalent thermodynamic temperature of observed and intrinsic monopole, expressing it in terms of the difference (Trombetti et al. 2021) ΔR = R − RBB, where, theoretically, RBB ≃ (1 − 2.5362 × 10−7) is the same ratio but for the case of the blackbody at the present temperature T0. Indeed, as explicitly shown by Eq. (9), the contribution from high-order derivatives appears also in a0, 0.
4.1. Interpolation versus derivatives
For a monopole frequency spectrum described by a tabulated function, the evaluation of the quantities  or
or  requires the interpolation of the corresponding functions in the adopted grid of points. Fornberg (1988, 1998) provided the weights for the (possibly centred) approximations at a grid point for the generation of finite difference formulas on arbitrarily spaced grids for any order of derivative. We are interested in evaluating derivatives from order zero up to order six. For a fixed number of grid points to be used in the differentiation scheme, nds, the order of accuracy decreases with the order of the derivative. We performed some tests increasing nds or fixing the order of accuracy and working with variable nds according to the order of derivative. We find no significant differences provided that at least the fourth order of accuracy at the highest derivative is achieved. For simplicity, we work with a fixed nds = 9, achieving the fourth order of accuracy up to the derivative of order six. For each value of
requires the interpolation of the corresponding functions in the adopted grid of points. Fornberg (1988, 1998) provided the weights for the (possibly centred) approximations at a grid point for the generation of finite difference formulas on arbitrarily spaced grids for any order of derivative. We are interested in evaluating derivatives from order zero up to order six. For a fixed number of grid points to be used in the differentiation scheme, nds, the order of accuracy decreases with the order of the derivative. We performed some tests increasing nds or fixing the order of accuracy and working with variable nds according to the order of derivative. We find no significant differences provided that at least the fourth order of accuracy at the highest derivative is achieved. For simplicity, we work with a fixed nds = 9, achieving the fourth order of accuracy up to the derivative of order six. For each value of  , that is, w = 0, (typically, for all the inner points of the grid), we select the grid point closest to
, that is, w = 0, (typically, for all the inner points of the grid), we select the grid point closest to  and four points on the left and four on the right to work with an almost centred approximation11. We can then directly compute the aℓ, 0 coefficients using the weights in Fornberg (1988) for the zero-order derivative in the desired value of w when using the equations in Sect. 2.1 (we call this the interpolation scheme), or the ones for the derivative from order zero up to order six but at w = 0 when using the equations in Sects. 2.2–2.3 (we call this the derivative scheme).
and four points on the left and four on the right to work with an almost centred approximation11. We can then directly compute the aℓ, 0 coefficients using the weights in Fornberg (1988) for the zero-order derivative in the desired value of w when using the equations in Sect. 2.1 (we call this the interpolation scheme), or the ones for the derivative from order zero up to order six but at w = 0 when using the equations in Sects. 2.2–2.3 (we call this the derivative scheme).
We add, in terms of antenna temperature, the background and the CMB BB monopole spectra and compute the corresponding aℓ, 0 coefficients12 using the interpolation and derivative schemes. In general, the aℓ, 0(ν, β)BB terms entering in the differences Δaℓ, 0 and ΔR are computed with the same treatment.
To focus on the issues raised applying the analytical solutions in Sects. 2.1–2.3 directly, we consider the reference cases based on the log–log polynomial characterisation of the ESMB and the analytical representation of the EDGES absorption profile (Sect. 3). We compute the monopole spectrum at each grid frequency and pollute it with a simulated noise to mimic potential inaccuracies affecting the functional representation of the background. These inaccuracies, and not the much larger real astrophysical model uncertainty, are indeed the types of errors that are amplified at the increasing derivative order. They are modelled as the sum of two terms added to the signal in terms of Tant to give
where G1 and G2 are extracted from Gaussian (pseudo)random realisations with zero average and unit variance; the dimensionless constant rerr determines the amplitude of the inaccuracies proportional to the signal; and the constant aerr gives the amplitude of the inaccuracies independently of the signal. Of course, setting rerr = aerr = 0, one can study the effect coming specifically from the discretisation associated with the adopted grid and from the adopted scheme. The results obtained in both the schemes can then be easily compared with those derived in the ideal fully analytical case.
The original tabular representations of the background monopole spectra already include their own potential inaccuracies. We therefore avoid adding any further simulated inaccuracy.
4.2. ESMB models
We apply the method described above to the ESMB discussed in Sect. 3.1. Assuming the polynomial representation to characterise the ESMB, Fig. 2 shows that the inaccuracies in the tabulated ESMB are almost proportional to the ESMB intensity and we then set aerr = 0. For conciseness, we report the case of the largest threshold Smax = 0.1 Jy, adopting a value of rerr = 2.5 × 10−4, which is an “average”, value between the maximum and minimum relative differences displayed in Fig. 2. The results at 1 ≤ ℓ ≤ 4 are shown in the left panels of Fig. 4. As expected, we also find that, for the choice rerr = aerr = 0, the agreement between the results based on both the interpolation and the derivative schemes and on the ideal fully analytical calculation is extremely good, and we therefore refrain from displaying this case in the figure, for simplicity. We also note that, including simulated noise, the interpolation and the derivative schemes give very similar results. Remarkably, even for rerr = 2.5 × 10−4, numerical uncertainties in the ESMB monopole spectrum propagate to higher ℓ, as evident from the figure already at ℓ = 2, and their effect dramatically increases with ℓ, making the Δaℓ, 0 computation highly unstable. The effect is particularly evident where Δaℓ, 0 should present the change of sign and, in general, at low values of Δaℓ, 0.
 |
Fig. 4. Comparison between the interpolation and the derivative schemes with the ideal fully analytical treatment applied to the analytical representations of the ESMB (left column) and the 21 cm EDGES profile (right column) considering |
The same analysis applied to the original tabulation, reported in Appendix A for simplicity, gives almost the same result, indicating that the above issue is indeed due to intrinsic uncertainties present in the calculation of the ESMB spectrum. Also, the similarity between the amplitude of the effect found in the two cases suggests that rerr = 2.5 × 10−4 represents a reasonable choice for globally characterising the inaccuracies in the ESMB tabulated spectrum for Smax = 0.1 Jy.
4.3. Redshifted 21 cm line models
We perform the same kind of analysis for the redshifted 21 cm line. To estimate representative values of rerr and aerr, we consider the results discussed in Bevins et al. (2021b) regarding the overall uncertainty of numerical codes for the prediction of the global 21 cm signal. According to these latter authors, their current precision is of about a few per cent or, in an absolute sense, around the mK level. Here, we consider values of rerr and aerr that are around an order of magnitude lower, as we are interested in the uncertainty within relatively narrow frequency ranges comparable to those adopted in the implementation of the differentiation scheme that covers about ten points of the grid, and also in view of the great future efforts expected in this field. Therefore, we first consider the analytical representation of the EDGES absorption profile and adopt rerr = 10−3. The results at 1 ≤ ℓ ≤ 4 are shown in the right panels of Fig. 4. Also in this case, for rerr = aerr = 0, we verified the extremely good agreement between both the interpolation and the derivative schemes and the ideal fully analytical calculation, as well as that, in general, the interpolation and the derivative schemes give very similar results. As found in the case of the ESMB, numerical uncertainties in the redshifted 21 cm line monopole spectrum clearly propagate to higher ℓ and their effect significantly increases with ℓ, which is particularly evident at low values of Δaℓ, 0 and around frequencies corresponding to the sign changes whose occurrence increases with ℓ.
With respect to the case rerr > 0 and aerr = 0, for rerr = 0 and aerr > 0 the effect of numerical uncertainties is relatively smaller (larger) at larger (smaller) absolute values of Δaℓ, 0 (Appendix B).
In general, we find that for larger numerical uncertainties, the error propagation effect appears even at ℓ = 1, as shown for the ESMB and the EDGES absorption profile in Appendices C and D, respectively, where we report the instability mitigation achieved with the methods presented in the following section, considering, for instance, values of rerr one order of magnitude larger or smaller than the reference values adopted above.
Finally, we tested the impact of a different assumption for the reference background in the calculation of Δaℓ, 0. For example, we considered an overall radio background at low frequency represented by Eq. (5) of Sect. 3 of Dowell & Taylor (2018). As expected, the results expressed in terms of Δaℓ, 0 do not change with respect to those reported in Fig. 4.
5. Filtering
In the previous section, we show that inaccuracies in the tabulated monopole frequency spectrum can prevent a robust and accurate computation of its transfer to higher multipoles. To solve this problem, we describe a prefiltering method (Sect. 5.1) that can be used independently of or in combination with the subsequent filtering techniques (Sects. 5.2 and 5.3), which, in turn, can also be applied independently.
5.1. Prefiltering of the monopole spectrum
A first approach is based on the prefiltering of the tabulated monopole frequency spectrum in order to smooth out inaccuracies occurring at small scales in a suitable equally spaced real space variable, u. We consider a low-pass Gaussian filtering in the Fourier space: we (i) first compute13 the fast Fourier transform (FFT) of the monopole spectrum tabulated in a grid ui (i = 1, Np, with Np a power of 2), then (ii) smooth it out at the modes, fi = 1, Np, corresponding to the small scales in the real space, and finally (iii) obtain a filtered monopole spectrum applying the inverse FFT (FFT−1) to the smoothed FFT, namely
where in (iii) we take the real part, because  is a real function. In Eq. (24), σf = fNp, where f determines the level of smoothing, which decreases for increasing f, in terms of fraction of modes. We tested the effect of different values of f in a range from ≃0.05 to ≃0.2, larger (smaller) values typically resulting in a negligible smoothing (in an excessive smoothing, possibly significantly affecting the original background shape). The filter in Eq. (24) is symmetric around the central mode according to the convention adopted for the FFT. Given the tabulations described in Sects. 3.1 and 3.2, we adopt u = log ν or u = 1 + z for the ESMB and 21 cm line models, respectively. We work typically with Np = 29 = 512. In the case of the redshifted 21 cm line, the original grid consists of slightly fewer than 512 points, but it can easily be extended considering that the global signal can be set to zero at z < 5.
is a real function. In Eq. (24), σf = fNp, where f determines the level of smoothing, which decreases for increasing f, in terms of fraction of modes. We tested the effect of different values of f in a range from ≃0.05 to ≃0.2, larger (smaller) values typically resulting in a negligible smoothing (in an excessive smoothing, possibly significantly affecting the original background shape). The filter in Eq. (24) is symmetric around the central mode according to the convention adopted for the FFT. Given the tabulations described in Sects. 3.1 and 3.2, we adopt u = log ν or u = 1 + z for the ESMB and 21 cm line models, respectively. We work typically with Np = 29 = 512. In the case of the redshifted 21 cm line, the original grid consists of slightly fewer than 512 points, but it can easily be extended considering that the global signal can be set to zero at z < 5.
We then replace  with
with  to work with a smoothed version of the original tabulation. Finally, we proceed to the calculation of the differences Δaℓ, 0 and ΔR, as in Sect. 4.
to work with a smoothed version of the original tabulation. Finally, we proceed to the calculation of the differences Δaℓ, 0 and ΔR, as in Sect. 4.
Figures 5 and 6 show two examples of the effect of the prefiltering applied with f = 0.1 to the ESMB and to the redshifted 21 cm line. This was carry out in very narrow intervals of the equally spaced variable u in order to make the effect clearly visible given the large variation of the signal on a wide range of u. We compare the analytical reference models without any error or adding errors extracted from a Gaussian random realisation, as discussed in Sect. 4, and the corresponding filtered ones. As emerges from the figures, the prefiltering produces a small change in the original monopole spectrum. For the ESMB, this change is less than ≃0.3% in the considered frequency range (see Fig. 1), while for the 21 cm line, as one might expect because of its sharp profile, the relative change is always less than ≃5%, being of ≃1% on average in the frequency range ν ∈ [66, 90] MHz, centred around 78 MHz, where the HI absorption profile is significant.
 |
Fig. 5. Comparison between the original signals represented by the polynomial interpolations in log–log of the ESMB without any error or adding relative errors and the corresponding filtered ones. We display the signal according to the original tabulation which is equally spaced in log ν, and multiply the antenna temperature by a certain power of the frequency to better visualise small-scale effects due to the added noise superimposed to the general trend. We consider a narrow frequency interval corresponding to nine grid points, as in those adopted in the differential scheme to numerically compute subsequent derivatives (Sect. 5). See legend and text. |
 |
Fig. 6. As in Fig. 5, but for the original signal represented by the EDGES analytical profile. The signal is displayed according to the original tabulation which is equally spaced in 1 + z. See legend and text. |
The most remarkable effect is instead the clear smoothing of the fluctuations introduced by the noise, which results in a significant mitigation of the instability in the calculation of the differences Δaℓ, 0 and ΔR (Sect. 6).
5.2. Filtering of derivatives
A second (or subsequent) approach is based on the filtering of the derivatives computed using the centred approximation numerical derivative scheme given in Fornberg (1988). We considered three different methods.
5.2.1. Filtering in real space
For each ui grid point, we initially compute the first derivative at all the nds contiguous points, uj, as in the Fornberg (1988) scheme. We then apply a low-pass Gaussian filter14 in real space to smooth out the first derivative in the ui point, which is estimated as an average over the nds points uj with weights of
where σG determines the level of smoothing, which increases with σG. Possible suitable values of σG of about  are suggested by the considered problems. Indeed, a step of 0.1 − 0.2 in log ν corresponds to a full width at half maximum (FWHM) bandwidth in frequency of a few tens of percent, which is comparable with that usually adopted in microwave experiments, while the tabulation used here for the redshifted 21 cm line models has a step of 0.1 in 1 + z.
are suggested by the considered problems. Indeed, a step of 0.1 − 0.2 in log ν corresponds to a full width at half maximum (FWHM) bandwidth in frequency of a few tens of percent, which is comparable with that usually adopted in microwave experiments, while the tabulation used here for the redshifted 21 cm line models has a step of 0.1 in 1 + z.
Subsequently, we compute the second derivative for each point as the first derivative of the filtered first derivative as evaluated above, and again smooth it out. We iterate this scheme up to the sixth-order derivative. At this point, we can evaluate the filtered derivative of any order at the desired frequencies, that is, at the set of  following the derivative scheme (Sects. 2.2–2.3). Here, we use the weights in Fornberg (1988) for the zero-order derivative; that is, interpolating over the grid of filtered derivatives. In practice, just the weights for the derivative of orders zero and one are used in this method.
following the derivative scheme (Sects. 2.2–2.3). Here, we use the weights in Fornberg (1988) for the zero-order derivative; that is, interpolating over the grid of filtered derivatives. In practice, just the weights for the derivative of orders zero and one are used in this method.
Theoretically, it is possible to choose different σG values at each iteration in order to optimise the filter according to the amplitude of the fluctuations occurring at a given derivation step. In some cases, we tested this option without finding a clear significant benefit, and so we decided to keep the σG value fixed for all the steps.
In principle, this real space filter can also be applied as prefiltering of the tabulated monopole frequency spectrum, replacing the method described in Sect. 5.1. However, in this context, the results are a little worse.
5.2.2. Filtering in Fourier space
As an alternative to the filtering in real space, we can filter the derivatives in the Fourier space. For all the points, ui, of the adopted grid we first compute the derivative using the scheme in Fornberg (1988). We then smooth it out using the same method described in Sect. 5.1, but applied to the derivatives with order larger than zero. In principle, the choice of f can also be adjusted according to the order of derivative, but again we do not find a clear significant advantage from this.
For this approach, we implemented two different methods.
-
Filtering sequentially: as in Sect. 5.2.1, we compute the first derivative; we then smooth it out as in Sect. 5.1. Subsequently, we evaluate the second derivative as the first derivative of the first derivative filtered in Fourier space, and again smooth it out; we iterate this scheme up to the sixth derivative. As before, only the weights for the derivative of orders zero and one are used here.
-
Filtering at once: we compute the derivatives from order zero to order six using the corresponding weights. For derivative orders larger than zero, we then independently smooth each derivative out using the filter in Sect. 5.1.
Above, we compute these filtered derivatives on the adopted grid. We then evaluate the filtered derivative at the desired frequencies, that is, at the set of  as required by the derivative scheme, using the weights in Fornberg (1988) for the zero-order derivative, that is, for interpolating over the grid of filtered derivatives.
as required by the derivative scheme, using the weights in Fornberg (1988) for the zero-order derivative, that is, for interpolating over the grid of filtered derivatives.
5.3. Boosting amplification and deamplification
As anticipated in Sect. 1 and shown in Sect. 4, the instabilities in the direct calculation of the aℓ, 0(ν, β) coefficients mainly come from the uncertainty in the monopole frequency spectrum at small scales combined with the necessity to perform a fine comparison of the very small differences between signals at very close frequencies, that is, of the order of the Doppler shift in frequency, δν, which is much smaller than the resolution of the tabulation grid. At the same time, in general and in particular for feature-rich spectral shapes, it is not possible to significantly degrade the adopted grid resolution in order to avoid degrading the available information about the spectrum shape. Conversely, for a hypothetical observer with a much higher speed, that is, higher by a significant factor fa than the real one with respect to the frame at rest with the considered background, the frequency Doppler shift would be correspondingly larger. This implies a comparison between signals at frequencies that consequently differ much more than in the case of the real speed of the observer, potentially decreasing the relative impact of uncertainties.
The above considerations suggest that is would be advantageous to investigate the possibility of performing the calculation of the aℓ, 0(ν, β) coefficients assuming an amplified speed value, βa = faβ (obviously keeping βa < 1), and then to properly rescale them to the real value of β. To this aim, we can exploit the scaling rules between derivatives given in Sect. 2.3. In principle, larger values of βa result in larger differences between the relevant frequencies. In practice, for each considered observational frequency, ν, we need to work locally according to the available tabulation grid, or, in other words, we need to avoid excessively large values of fa that are able to move the relevant frequencies outside the range identified by the set of points (typically, nds = 9) used in the differentiation scheme in order to retain as much information as possible about the spectrum shape. From Eq. (3), we have
The condition |w|≤1 implies
of course, both ν′> ν (blueshift) and ν′< ν (redshift) are permitted.
Instead, we are here interested in finding the implications for β (in the range 0 < β < 1) coming from the system of the two conditions w ≤ 1 and w ≥ −1 in order to estimate suitable values of βa. After some algebra, these give, respectively,
and
where, clearly, the former is only non-trivial for ν′< ν, and the latter is only non-trivial for ν′> ν.
As discussed above, we need to work locally around ν. Among the nds frequency points used in the differentiation scheme, let us consider two frequencies, ν′=νL < ν equal to the lowest frequency and ν′=νR > ν equal to the highest one. We consider the system of the two conditions (28) and (29) for νL and νR, respectively; its solution, that is, the strongest of the two conditions, depends on the type of grid adopted. For the tabulations used in this work, which has an equally spaced step in log ν or in 1 + z, the step in ν increases with frequency, and so |νR − ν|> |νL − ν| and the strongest condition correspond to Eq. (29). We then chose
We note that this does not necessarily imply working with fixed fa (or βa) for the whole considered frequency range. On the contrary, the value of fa to be used in this approach is determined by the kind of the tabulation grid used and its resolution. For example, for an equally spaced grid in log ν, the value of fa is constant for all the grid points, while for an equally spaced grid in 1 + z ∝ 1/ν, fa increases with ν. In general, the value of fa increases for decreasing resolution (or increasing step).
It is easy to check that setting β = βa and ν′=νR in Eq. (26) results in w = −1. We write νR = ν + Δ and νL = ν − Δ + δ, with Δ > 0 and δ > 0, where, given the properties of the considered grids, we locally obtain δ of less than Δ by a significant factor and Δ ≪ ν. Therefore, setting β = βa and ν′=νL in Eq. (26), we have w = 1 + 2(Δ2 − νδ − Δδ)/(Δ2 + 2νΔ)∼1 − δ/Δ, which is a value of slightly less than 1. This shows that this choice of βa allows us to work within a range of Doppler-shifted frequencies that essentially span the same range [νL, νR] around ν adopted in the differentiation scheme, while for the real value of β they are much closer to ν15.
We can compute the aℓ, 0(ν, β) coefficients for βa using both the interpolation scheme and the derivative scheme (Sect. 4.1). Equation (21) then allows us to rescale the result to the real value of β. In the interpolation scheme, this rescaling can be globally performed applying it as in the case of the leading derivative, of order equal to ℓ, while, in the derivative scheme, this rescaling can be performed for each derivative order.
This method, specifically designed for the problem under consideration, acts as a filter; in the presence of numerical uncertainties, it allows us to compare the variations of the monopole frequency spectrum under more numerically stable conditions.
6. Filtering results
6.1. Prefiltering
We study the efficiency of the prefiltering method described in Sect. 5.1. We report the results obtained for a level of smoothing characterised by f = 0.1.
6.1.1. ΔR
First, we consider the mitigation effect of the prefiltering on the estimation of the observed monopole, expressed in terms of the difference ΔR (see Sect. 4 for its definition).
Figure 7 shows this difference assuming the analytical representation of the ESMB signal for the maximum value of the detection threshold and a relative error of rerr = 2.5 × 10−4, including or not including the smoothing. As, in principle, expected from Eq. (9), the propagation of the uncertainty in the intrinsic monopole spectrum affects the calculation of the observed spectrum, introducing instabilities in the direct calculation that are strongly suppressed by the prefiltering.
 |
Fig. 7. ΔR evaluated assuming the analytical representation of the ESMB with a detection threshold of Smax = 0.1 Jy, considering a relative error and including or not including the prefiltering. The curve corresponding to the ideal case is almost superimposed on the green curve, and therefore it is not reported for simplicity. Here (and in the following analogous figures), solid (dots) lines refer to positive (negative) values. See legend for an explanation of the symbols and lines. |
Figure 8 refers to the 21 cm line EDGES profile, assuming rerr = 10−3. As in this case the prefiltering effect on the original monopole spectrum is not expected to be as small as in the other cases (Sect. 5.1), for comparison we also display the result obtained in the absence of uncertainties. Although we find that the prefiltering introduces a little smoothing excess at frequencies around the relative minima and maxima of ΔR, it mainly results in a very good mitigation of the artefacts induced by the propagation of numerical uncertainties in the direct calculation.
 |
Fig. 8. ΔR evaluated assuming the analytical representation of the EDGES profile including or not a relative error and the prefiltering. See legend for an explanation of the symbols and lines. |
In the presence of observer motion, this test underlines the relevance of filtering the original tabulated intrinsic monopole spectrum for a stable and accurate estimation of the observed one.
6.1.2. ℓ ≥ 1
As seen in Fig. 4, the effect of the propagation of numerical uncertainties strongly increases with the multipole, and is remarkable even at ℓ = 2. Here, we focus on the mitigation achieved with the prefiltering using the interpolation and derivative schemes. The results are shown in Fig. 9 for the ESMB (left column) and the 21 cm EDGES profile (right column), where they are compared with the ideal fully analytical treatment. The method provides a good estimation of the spectrum up to ℓ = 2, a reasonable mitigation of the instabilities at ℓ = 3, but is less effective from ℓ = 4. The advantage conferred by further applying the filters discussed in Sects. 5.2 and 5.3 to the signal is described in the following sections.
 |
Fig. 9. As in Fig. 4, but including prefiltering with f = 0.1 and rerr as before. See legend for an explanation of the symbols and lines. |
6.2. Filtering
Hereafter, we present the results derived for the different filtering techniques discussed above; we describe these separately for the two investigated backgrounds.
6.2.1. ESMB: Analytical model
In this section, we compare the spherical harmonic coefficients obtained for the ESMB with the described filters up to ℓ = 6, starting from the original monopole pre-filtered as described in Sect. 5.1 with the same parameters as in Sect. 6.1. Specifically, the left column of Fig. 10 shows the results of the FFT derivative filtering approach applied at once or sequentially, the real space filter and the reference ideal case. These last two curves are also compared with the approach based on boosting amplification and deamplification for both the interpolation and the derivative schemes (right column of Fig. 10). From the plots, and in agreement with the results already obtained applying only the prefiltering, we see that all the methods accurately reproduce the spectrum up to ℓ = 2. Furthermore, although with different efficiency, all of them provide a further mitigation of the instabilities at ℓ = 3 with respect to the case of prefiltering alone (Fig. 9): this is particularly evident in the case of the filtering of derivatives – in both real and Fourier space – and with boosting amplification and deamplification in the interpolation scheme. The differences between the results obtained with the different filters increase at increasing multipole. At ℓ = 4, the filtering with boosting amplification and deamplification, particularly in the derivative scheme, and also the FFT derivative filtering applied at once do not produce a significant further mitigation with respect to the case of prefiltering alone, and their efficiency degrades at increasing ℓ. On the contrary, filtering the derivatives in sequence allows us to significantly mitigate the propagation of the monopole uncertainties up to the maximum multipole investigated, working in both Fourier and real space. We note that the latter is found to be more stable than the former even around frequencies where, for odd ℓ, Δaℓ, 0 changes in sign or, in general, where it assumes low values.
 |
Fig. 10. Comparison between the different filtering methods and the ideal fully analytical case, starting from the analytical formulation of the ESMB including the relative error and the prefiltering as before. See legend and text. |
In Appendix C, we report a few representative cases to illustrate the validity of the method for different uncertainties in the monopole spectrum.
6.2.2. ESMB: Tabulated models
We derived the spherical harmonic coefficients for the ESMB tabular representations under study. As expected, the quality of the predictions does not vary significantly with the assumed threshold. Therefore, for simplicity, we report the results only for two different values of Smax. Figure 11 shows the spectra up to ℓ = 4 for Smax = 0.01 Jy and 0.05 Jy. The latter is multiplied by a factor of 3.5 to better distinguish the curves. In the figure, prefiltering is applied. As in the analytical case, the best and more stable filtering approach is found to be the Gaussian filter in real space, which works very well except at ℓ = 4 near the low-frequency boundary and for very low values of Δa4, 0 because of the presence of small oscillations.
 |
Fig. 11. Comparison between the real space filter method applied to the ESMB tabulated intensity calculated adopting two different thresholds and the corresponding ideal, fully analytical cases. See legend and text. |
6.2.3. Redshifted 21 cm line: EDGES
The improvement in the reconstruction of the spectrum with the above filters, up to ℓ = 6, is shown in Fig. 12 for the analytical EDGES profile of the 21 cm line. In this case, we note the aforementioned smoothing excess in the spectrum at ℓ = 2, already found by applying just the prefiltering, which persists around the relative minima and maxima and in the high-frequency region. The latter effect is likely due to the poorer resolution, δν/ν, at increasing frequency because of the adopted grid, and it is further amplified by applying the sequential FFT filter. In general, the spectrum is well reproduced up to ℓ = 3, in particular for the real space and the boosting amplification and deamplification filters, and a slight refinement is achieved at ℓ = 4. At higher multipoles, these filtering methods allow a reasonable estimation of the spectrum.
In Appendix D, we probe the validity of the method for different uncertainties in the monopole spectrum, focussing in particular on the possibility of reducing the smoothing excess induced by the prefiltering depending on the intrinsic accuracy of the model and the multipole of interest.
6.2.4. Redshifted 21 cm line: Tabulated models
The monopole spectra predicted by the tabulated models described in Sect. 3.2 are very different and cannot be easily characterised by analytical representations; the same holds at higher multipoles.
On the other hand, on the basis of the previous results, we are confident that the two best filtering approaches, namely the real space and the amplification and deamplification approaches, provide a reasonable prediction of the spectrum up to ℓ = 4. As shown in Fig. 13 for the A, B, and C models (left column) and for the D, E, and F models (right column), the two methods give very similar results.
 |
Fig. 13. Results for the six considered 21 cm line tabulated models applying the prefiltering and the two best filtering methods: the real space filter and the boosting amplification and deamplification in the interpolation scheme. In order to better distinguish the six models, the y-scale differs from that of Fig. 12. See legend and text. |
7. Discussion and conclusion
In this paper, we study how to compute the boosting effects produced by the observer peculiar motion. This latter modifies and transfers the isotropic monopole frequency spectrum to higher multipoles (Sects. 2 and 2.1), beyond the case of cosmic or extragalactic backgrounds well characterised by analytical or semi-analytical functions. Indeed, monopole frequency spectra described by tabular representations are typically affected by uncertainties; if these latter are negligible, the adopted interpolation or derivative scheme (Sect. 4.1) gives results with accuracy similar to that achieved in the case of analytical or semi-analytical functions (Sects. 4.2 and 4.3). On the other hand, these uncertainties propagate and increase with the derivative order, possibly preventing the accurate computation of its transfer to higher multipoles and also of the observed monopole (Sects. 4.2, 4.3 and 6.1.1 and Appendices A and B). We developed methods to filter (Sect. 6.2) the original tabulated function or its derivatives, and ultimately the multipole spectra, and identified approaches for deriving reliable predictions for a wide range of background models.
For monopole frequency spectra that can be expanded in Taylor’s series, we derived explicit expressions for the harmonic coefficients in terms of monopole spectrum derivatives (Sect. 2.2), performing our calculation up to ℓ = 6. We considered different types of filters: Gaussian prefiltering in Fourier space of the tabulated function (Sect. 5.1 and, for applications, Sect. 6.1); Gaussian filtering in real space of the numerical derivatives in sequence (Sect. 5.2.1); Gaussian filtering in Fourier space of the numerical derivatives, both in sequence and all at once (Sect. 5.2.2); and a dedicated method of amplification and deamplification of the boosting (Sect. 5.3) in the interpolation and derivative schemes. We applied them to two very different types of signal, usually represented by tabulated functions, namely the (smooth) ESMB (Sect. 3.1) and the (feature-rich) redshifted 21 cm line (Sect. 3.2), superimposed to the CMB. We tested these approaches by applying them to analytical approximations computed on the adopted tabulation grids and polluted with simulated noise (Sect. 4.1).
A comparison of the accuracy in calculating the spherical harmonic expansion coefficients using the explicit analytical solutions reported in Sect. 2.1 or the standard formal inversion of Eq. (4) – which is based on the computation of an integral of the considered monopole background spectrum multiplied by a renormalised associated Legendre polynomial – has already been presented in Trombetti et al. (2021, see their Eq. (5) for the latter method). The formal inversion is performed through a precise quadrature at each ℓ, which requires the evaluation of the integrand function for a very large number of points (typically from hundreds or thousands or more, depending on ℓ and on the spectral shape), while the direct analytic solutions at 0 ≤ ℓ ≤ 6 given in Sect. 2.1 only require that we evaluate the monopole background spectrum in seven points, thus reducing the required computation time by orders of magnitude. Indeed, the running time needed for the fully analytical approach depends on the complexity of the functional form, and it is found to be larger for the EDGES profile (∼25 ms) than for the ESMB (∼3 ms)16.
For the various models of the two types of background, the running time is of the order of ∼4 − 5 ms for prefiltering, ∼200 − 300 ms for the boosting amplification and deamplification accounting for both the interpolation and derivative schemes, and ∼350 − 450 ms for the Fourier and real space filters. Without any filtering, applying the direct computation on tabulated models with the interpolation scheme, the running time is ∼160 − 190 ms. As the required execution times are obviously machine dependent, it is more meaningful to provide them in terms of the ratio, rt, between the time required for a computation with a certain type of filtering and that required by the direct explicit solutions in the interpolation scheme. This ratio is of particular interest for backgrounds for which it is difficult to find a suitable analytical representation. Remarkably, for both the backgrounds, rt ∼ 1.2 − 1.3 for the boosting amplification and deamplification with the two schemes together up to ∼2.2 − 2.3 for the Fourier or real space filters.
The results found indicate which methods, or their combinations, are the most appropriate for predicting the spherical harmonic expansion coefficients depending on the background shape, the accuracy of the tabular representation, and the multipole of interest.
For many types of smooth background spectra, it is feasible to find a set of analytical or semi-analytical functions that, in addition to characterising the monopole spectrum, provide information as to the main properties of its derivatives with respect to the frequency, or, more generally, of its tiny variations in very narrow frequency ranges. In particular, for the ESMB there is good agreement between the prediction up to high multipoles of a log–log polynomial description and that derived using a suitable filtering approach. In such conditions, the use of analytical representations is preferable.
On the other hand, feature-rich background monopole spectra and their derivatives are typically difficult to describe with suitable analytical or semi-analytical representations, except for some specific cases. This holds, for instance, for the redshifted 21 cm line.
The best approach to manage smooth tabulated background spectra is found to be the combination of prefiltering in Fourier space of the monopole spectrum with a Gaussian filter of derivatives in real space applied in sequence. This method allowed us to find a robust prediction of the Δaℓ, 0 differences up to a certain ℓ, which depends on the intrinsic accuracy of the model. For the accounted reference uncertainty, rerr = 2.5 × 10−4, this technique works well up to at least ℓ = 4 (Sects. 6.2.1 and 6.2.2); for uncertainties one order of magnitude smaller (larger) the maximum multipole for a reliable estimate is ℓ = 6 (ℓ = 3); see Appendix C.
When dealing with feature-rich tabulated spectra, such as the 21 cm models considered in this paper, we find that prefiltering in combination with the real space or the boosting amplification and deamplification filtering is the best approach to predict the spherical harmonic coefficients up to ℓ = 4 (Sects. 6.2.3 and 6.2.4). For relative uncertainties rerr ≲ 10−4, we argue that these methods provide good estimates up to ℓ = 6 (Appendix D). For such small intrinsic uncertainty of the model and depending on the multipole of interest, the prefiltering can be avoided in order to reduce the little smoothing excess it might introduce, resulting into an improvement for the dipole and the quadrupole (Appendix D).
The developed methods can significantly extend the range of manageable models beyond the case of backgrounds characterised a priori by analytical or semi-analytical functions, requiring only an affordable increase in computational time compared to direct calculation performed simply by interpolating the available tabular representations.
Obviously,  ; we keep here the derivative index according to the notation in Fornberg (1988).
; we keep here the derivative index according to the notation in Fornberg (1988).
In principle, even in the absence of a good analytic or semi-analytic representation of the monopole spectrum over its entire frequency range, it could be possible to estimate Rn for different analytic representations among the more reasonable ones in a given frequency range of particular interest.
We always refer here to the most successful model discussed in that paper, called “C2Ex”. See Tucci et al. (2011), Sect. 4, for more details.
In the reminder of the present work, we show our results between 5 GHz and 500 GHz (see Fig. 1) where the model is better probed and not overwhelmed by other extragalactic background contributions, particularly at higher frequencies. Furthermore, working in a restricted frequency range allows us to be conservative in our approach with respect to potential boundary effects.
In passing, we note that this type of analytical function belongs to the set of derivative constrained functions discussed in Bevins et al. (2021a) and has been adopted in Niţu et al. (2021) to represent the cosmic radio background spectrum.
Some works alternatively explain the EDGES profile in terms of residual instrumental systematic effects (e.g., Sims & Pober 2020) or consider the impact of ionosphere (Shen et al. 2021), while the results of the Shaped Antenna measurement of the background RAdio Spectrum (SARAS) experiment (Singh et al. 2022) are not in agreement with the EDGES cosmological signal profile.
In general, the aℓ, 0(ν, β) should be computed separately, and, for different velocity directions, one can assume the z-axis parallel to each velocity and then rotate (Goldstein 1984) the aℓ, 0(ν, β) to a common reference system, implying that aℓ, m(ν, β) with m ≠ 0 do not vanish.
If the desired value of  is close to the first left (right) boundary point of the grid, we could consistently select more grid points on the right (left), resulting e.g. in an almost one-sided approximation. In practice, to fully prevent possible effects associated with the transition between the two types of approximations, we prefer to avoid the computation for the (nds − 1)/2 points closer to each of the grid extremes.
is close to the first left (right) boundary point of the grid, we could consistently select more grid points on the right (left), resulting e.g. in an almost one-sided approximation. In practice, to fully prevent possible effects associated with the transition between the two types of approximations, we prefer to avoid the computation for the (nds − 1)/2 points closer to each of the grid extremes.
Indeed, the types of background considered here are superimposed to the CMB. For simplicity, we consider here a Planckian law at temperature T0 for the CMB spectrum, although it could be replaced by a distorted CMB spectrum, as discussed in Trombetti et al. (2021) for analytic or semi-analytic functions.
In principle, because the condition (29), it is possible to work with βa larger than the one in Eq. (30) and a larger interval in the differentiation scheme, but relaxing the locality. Furthermore, even for the previous methods, more points can be used in the differentiation scheme if a tabulation with a finer grid is available, but at the cost of a corresponding increasing number of operations and not necessarily with better precision unless the finer tabulation is more accurate.
Acknowledgments
L.T. acknowledges the Spanish Ministerio de Ciencia, Innovación y Universidades for partial financial support under the projects PID2022-140670NA-I00 and PID2021-125630NB-I00. It is a pleasure to thank the anonymous referee for comments that helped improve the paper.
References
- Baiesi, M., Burigana, C., Conti, L., et al. 2020, Phys. Rev. Res., 2, 013210 [Google Scholar]
- Balashev, S. A., Kholupenko, E. E., Chluba, J., Ivanchik, A. V., & Varshalovich, D. A. 2015, ApJ, 810, 131 [Google Scholar]
- Bevins, H. T. J., Handley, W. J., Fialkov, A., et al. 2021a, MNRAS, 502, 4405 [NASA ADS] [CrossRef] [Google Scholar]
- Bevins, H. T. J., Handley, W. J., Fialkov, A., de Lera Acedo, E., & Javid, K. 2021b, MNRAS, 508, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [Google Scholar]
- Bonavera, L., Massardi, M., Bonaldi, A., et al. 2011, MNRAS, 416, 559 [NASA ADS] [Google Scholar]
- Bowman, J. D., Rogers, A. E. E., Monsalve, R. A., Mozdzen, T. J., & Mahesh, N. 2018, Nature, 555, 67 [Google Scholar]
- Burigana, C., Carvalho, C. S., Trombetti, T., et al. 2018, JCAP, 4, 021 [Google Scholar]
- Burigana, C., Trombetti, T., & Chierici, F. 2022, ASP Conf. Ser., 532, 143 [NASA ADS] [Google Scholar]
- Cohen, A., Fialkov, A., Barkana, R., & Lotem, M. 2017, MNRAS, 472, 1915 [Google Scholar]
- Cohen, A., Fialkov, A., Barkana, R., & Monsalve, R. A. 2020, MNRAS, 495, 4845 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
- Condon, J. J., Cotton, W. D., Fomalont, E. B., et al. 2012, ApJ, 758, 23 [Google Scholar]
- Danese, L., & De Zotti, G. 1981, A&A, 94, L33 [Google Scholar]
- Datta, R., Aiola, S., Choi, S. K., et al. 2019, MNRAS, 486, 5239 [NASA ADS] [CrossRef] [Google Scholar]
- Deshpande, A. A. 2018, ApJ, 866, L7 [Google Scholar]
- De Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [Google Scholar]
- De Zotti, G., Negrello, M., Castex, G., Lapi, A., & Bonato, M. 2016, JCAP, 3, 047 [Google Scholar]
- Dowell, J., & Taylor, G. B. 2018, ApJ, 858, L9 [Google Scholar]
- Everett, W. B., Zhang, L., Crawford, T. M., et al. 2020, ApJ, 900, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Forman, M. A. 1970, Planet. Space Sci., 18, 25 [Google Scholar]
- Fornberg, B. 1988, Math. Comput., 51, 699 [Google Scholar]
- Fornberg, B. 1998, SIAM Rev., 40, 685 [Google Scholar]
- Goldstein, J. D. 1984, J. Geophys. Res., 89, 4413 [Google Scholar]
- Gralla, M. B., Marriage, T. A., Addison, G., et al. 2020, ApJ, 893, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Huynh, M. T., Seymour, N., Norris, R. P., & Galvin, T. 2020, MNRAS, 491, 3395 [NASA ADS] [CrossRef] [Google Scholar]
- Konigl, A. 1981, ApJ, 243, 700 [Google Scholar]
- Lagache, G., Béthermin, M., Montier, L., Serra, P., & Tucci, M. 2020, A&A, 642, A232 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massardi, M., Bonaldi, A., Negrello, M., et al. 2010, MNRAS, 404, 532 [NASA ADS] [Google Scholar]
- Massardi, M., Ekers, R. D., Murphy, T., et al. 2011, MNRAS, 412, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Bonato, M., López-Caniego, M., et al. 2022, MNRAS, 513, 6013 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N. A., Bonzini, M., Fomalont, E. B., et al. 2013, ApJS, 205, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, S., Silk, J., & Wandelt, B. D. 2018, MNRAS, 477, 4473 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Niţu, I. C., Bevins, H. T. J., Bray, J. D., & Scaife, A. M. M. 2021, Astropart. Phys., 126, 102532 [CrossRef] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, E., Anstey, D., de Lera Acedo, E., Fialkov, A., & Handley, W. 2021, MNRAS, 503, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Sims, P. H., & Pober, J. C. 2020, MNRAS, 492, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, S., Jishnu, N. T., Subrahmanyan, R., et al. 2022, Nat. Astron., 6, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Slosar, A. 2017, Phys. Rev. Lett., 118, 151301 [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017, A&A, 602, A1 [Google Scholar]
- Toffolatti, L., Argueso Gomez, F., De Zotti, G., et al. 1998, MNRAS, 297, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Tompkins, S. A., Driver, S. P., Robotham, A. S. G., et al. 2023, MNRAS, 521, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Trombetti, T., & Burigana, C. 2019, A&A, 631, A61 [EDP Sciences] [Google Scholar]
- Trombetti, T., Burigana, C., & Chierici, F. 2021, A&A, 646, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tucci, M., & Toffolatti, L. 2021, A&A, 650, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tucci, M., Toffolatti, L., De Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Instability for ESMB tabulated model
Assuming an ESMB described in terms of a tabulated function for the largest threshold Smax = 0.1 Jy (Sect. 3.2) and using the interpolation and derivative schemes described in Sect. 4.1, we report in Fig. A.1 the results obtained when directly applying the analytical solutions given in Sects. 2.1–2.3 and compare them with the ideal, fully analytical calculation and the results discussed in Sect. 4.2 (see Fig. 4). As evident from the figure, the intrinsic uncertainties in the original tabulation of ESMB monopole spectrum propagate to higher ℓ, already at ℓ = 2, and their effect dramatically increases with ℓ, making the Δaℓ, 0 computation highly unstable, similarly to the case of the corresponding polynomial representation polluted with numerical uncertainties.
 |
Fig. A.1. As in the left column of Fig. 4, but for the ESMB described by the original tabulated function. See legend. |
Appendix B: Absolute error instability: EDGES
We directly apply the solutions (Sects. 2.1–2.3) to the analytical representation of the EDGES absorption profile (Sect. 3.2), but polluted with inaccuracies independent of the signal and parametrised by a constant absolute error aerr (see Eq. (23)). The results are summarised in Fig. B.1 for the interpolation and derivative schemes described in Sect. 4.1. We assume aerr = 0.1 mK, a value that is about an order of magnitude lower than the absolute uncertainty quoted here, analogously to that of rerr adopted in Sect. 4.3, for a comparison with the results discussed in that section (see Fig. 4) and with the ideal fully analytical calculation.
As emerges from the figure, the effect of numerical uncertainties is relatively smaller (larger) at larger (smaller) absolute values of Δaℓ, 0 with respect to the case of inaccuracies proportional to the signal: remarkably, the two positive peaks at ℓ = 2 and the positive peak between 80 MHz and 90 MHz at ℓ = 3 are now less affected than in Fig. 4, while numerical uncertainties degrade the quality of the signal prediction at small absolute values of Δaℓ, 0.
 |
Fig. B.1. As in the right column of Fig. 4, but for rerr = 0, aerr = 0.1 mK and for ℓ ≤ 3. See legend. |
Appendix C: Uncertainty dependence: ESMB
 |
Fig. C.1. Comparison between the real space filter without and with prefiltering, the original case and the ideal, fully analytical case, starting from the analytical formulation of the ESMB for rerr = 2.5 × 10−3 and Smax = 0.1 Jy. See legend and text. |
We investigated how different values of the relative error impact the spectrum prediction. For comparison with previous cases, we considered the ESMB analytical model with Smax = 0.1 Jy. Figure C.1 shows the spherical harmonic expansion coefficients up to ℓ = 4 for rerr = 2.5 × 10−3, one order of magnitude greater than the reference error adopted in this work, applying or not applying the prefiltering and compare them with the fully analytical approach and the original treatment. As emerges from the figure, without applying any filter, the coefficients present non-negligible oscillations already at ℓ = 1; these increase at higher multipoles. These oscillations are significantly mitigated up to ℓ = 2 with the real space filter only, while the prefiltering plays an important role in damping the oscillations at ℓ ≥ 3.
As expected, by decreasing the value of the error to rerr = 2.5 × 10−5, the resulting coefficients are much more stable. For this reason, only the last two highest multipoles are shown in Fig. C.2. Here, the spectrum is very well reproduced also without the prefiltering step, albeit with increasing oscillations at low signal values. Compared with the reference case, we note a small increase in the predicted Δaℓ, 0 values, especially at ℓ = 6.
 |
Fig. C.2. As Fig. C.1 but without the original case, for rerr = 2.5 × 10−5 and for ℓ = 5 and 6. See legend. |
Appendix D: Uncertainty dependence: EDGES
Analogously to Appendix C, we study the impact of different relative uncertainties on the prediction of the spectra for the analytical EDGES profile. As before, we first consider rerr = 10−2, which is an order of magnitude greater than the reference value previously assumed. In Fig. D.1 we show the results – up to ℓ = 2 – with and without the prefiltering for the two best filters and compare them with the ideal and the original cases. As already evident from Sect. 5.1, the prefiltering attenuates the fluctuations, particularly for the real space filter for the dipole (ℓ = 1), and it becomes more relevant in the reconstruction of the expected spectral shape for the quadrupole (ℓ = 2) for both filters.
On the contrary, for a significantly smaller uncertainty, the dipole spectrum is very well reproduced without the prefiltering but applying the real space filter or the boosting amplification and deamplification, as evident from the comparison between the first and the third panel in the left column of Fig. D.2, where rerr = 10−4. The same conclusion holds for the quadrupole (compare second and fourth panels in the left column), where the two positive maxima better agree with the ideal case; although the relative minimum around 80 MHz exhibits some small oscillations. Instead, for the spectrum prediction at the highest multipoles (see the right column of the same figure), the mere use of one of the two above best filters does not substantially attenuate the instabilities, while this is possible when these filters are preceded by prefiltering, which therefore represents a fundamental step.
 |
Fig. D.1. Comparison between the two favourite filters including (two bottom panels) or not including (two top panels) the prefiltering, the original case, and the ideal, fully analytical case for the EDGES profile for rerr = 10−2. See legend. |
 |
Fig. D.2. As in Fig. D.1 but without the original case, for rerr = 10−4 at ℓ = 1 and 2 (left column) and at ℓ = 5 and 6 (right column). See legend. |
Appendix E: Contribution from higher-order derivatives
Let us return to the concept, anticipated at the end of Sect. 2.2, focussing on the dipole and on the basis of the results obtained in the present study. Considering Eq. (12) at the leading order, we have  . Inserted in Eq. (10) taken up to the third-order derivative, this implies
. Inserted in Eq. (10) taken up to the third-order derivative, this implies  , where
, where  includes only the first-order derivative contribution to a1, 0. The differences Δaℓ, 0 have different frequency dependences at different ℓ, and, in particular, they exhibit sign changes at frequencies that are different at each ℓ (Trombetti et al. 2021). Thus, in the frequency ranges around these sign inversions, neglecting the terms from higher-order derivatives clearly implies significant relative errors in the Δaℓ, 0 calculation even at ℓ = 1. For example, in the case of the 21cm line, the comparison between the values of Δa1, 0 and Δa3, 0 in the right panel of Fig. 4 shows that, at frequencies around ≃73.5 MHz, neglecting the contribution from
includes only the first-order derivative contribution to a1, 0. The differences Δaℓ, 0 have different frequency dependences at different ℓ, and, in particular, they exhibit sign changes at frequencies that are different at each ℓ (Trombetti et al. 2021). Thus, in the frequency ranges around these sign inversions, neglecting the terms from higher-order derivatives clearly implies significant relative errors in the Δaℓ, 0 calculation even at ℓ = 1. For example, in the case of the 21cm line, the comparison between the values of Δa1, 0 and Δa3, 0 in the right panel of Fig. 4 shows that, at frequencies around ≃73.5 MHz, neglecting the contribution from  implies relative errors on Δa1, 0 above the per cent level; that is, well above the level quoted on simple scaling rules. Figure E.1 shows the relative contribution to Δa1, 0 from derivatives of orders greater than one. Similar considerations hold for other types of background and this issue is clearly exacerbated when considering combinations of signals with different amplitudes and spectral behaviours, for which the frequency range where this effect occurs, is a priori unknown. On the contrary, including higher-order terms in the calculation strongly mitigates this issue.
implies relative errors on Δa1, 0 above the per cent level; that is, well above the level quoted on simple scaling rules. Figure E.1 shows the relative contribution to Δa1, 0 from derivatives of orders greater than one. Similar considerations hold for other types of background and this issue is clearly exacerbated when considering combinations of signals with different amplitudes and spectral behaviours, for which the frequency range where this effect occurs, is a priori unknown. On the contrary, including higher-order terms in the calculation strongly mitigates this issue.
 |
Fig. E.1. Percentage difference between Δa1, 0 computed for the analytical description of the EDGES absorption profile using Eq. (10) with all the terms and taking only the contribution from the first-order derivative, in the ideal case without errors. We note that the expected divergence at a frequency of around ≃73.5 MHz disappears only due to frequency sampling. Solid (dots) lines refer to positive (negative) values. See text. |
All Tables
Model name, its corresponding row number and the seven key parameters for the 21 cm signals from the 21cmGEM code.
All Figures
 |
Fig. 1. Comparison among the tabulated intensities of the considered ESMB model (C2Ex) for the different detection thresholds Smax discussed in the main text. See legend for an explanation of the symbols and lines. |
| In the text | |
 |
Fig. 2. Absolute value of the difference between the log–log polynomial interpolations and the original tabulations (bottom curves) for the maximum and minimum detection thresholds adopted in the calculation of the ESMB total intensity (top curves). See legend for an explanation of the symbols and lines. |
| In the text | |
 |
Fig. 3. Comparison between the considered redshifted 21 cm line models. See legend and text. |
| In the text | |
 |
Fig. 4. Comparison between the interpolation and the derivative schemes with the ideal fully analytical treatment applied to the analytical representations of the ESMB (left column) and the 21 cm EDGES profile (right column) considering |
| In the text | |
 |
Fig. 5. Comparison between the original signals represented by the polynomial interpolations in log–log of the ESMB without any error or adding relative errors and the corresponding filtered ones. We display the signal according to the original tabulation which is equally spaced in log ν, and multiply the antenna temperature by a certain power of the frequency to better visualise small-scale effects due to the added noise superimposed to the general trend. We consider a narrow frequency interval corresponding to nine grid points, as in those adopted in the differential scheme to numerically compute subsequent derivatives (Sect. 5). See legend and text. |
| In the text | |
 |
Fig. 6. As in Fig. 5, but for the original signal represented by the EDGES analytical profile. The signal is displayed according to the original tabulation which is equally spaced in 1 + z. See legend and text. |
| In the text | |
 |
Fig. 7. ΔR evaluated assuming the analytical representation of the ESMB with a detection threshold of Smax = 0.1 Jy, considering a relative error and including or not including the prefiltering. The curve corresponding to the ideal case is almost superimposed on the green curve, and therefore it is not reported for simplicity. Here (and in the following analogous figures), solid (dots) lines refer to positive (negative) values. See legend for an explanation of the symbols and lines. |
| In the text | |
 |
Fig. 8. ΔR evaluated assuming the analytical representation of the EDGES profile including or not a relative error and the prefiltering. See legend for an explanation of the symbols and lines. |
| In the text | |
 |
Fig. 9. As in Fig. 4, but including prefiltering with f = 0.1 and rerr as before. See legend for an explanation of the symbols and lines. |
| In the text | |
 |
Fig. 10. Comparison between the different filtering methods and the ideal fully analytical case, starting from the analytical formulation of the ESMB including the relative error and the prefiltering as before. See legend and text. |
| In the text | |
 |
Fig. 11. Comparison between the real space filter method applied to the ESMB tabulated intensity calculated adopting two different thresholds and the corresponding ideal, fully analytical cases. See legend and text. |
| In the text | |
 |
Fig. 12. As in Fig. 10, but for the 21 cm EDGES profile. See legend. |
| In the text | |
 |
Fig. 13. Results for the six considered 21 cm line tabulated models applying the prefiltering and the two best filtering methods: the real space filter and the boosting amplification and deamplification in the interpolation scheme. In order to better distinguish the six models, the y-scale differs from that of Fig. 12. See legend and text. |
| In the text | |
 |
Fig. A.1. As in the left column of Fig. 4, but for the ESMB described by the original tabulated function. See legend. |
| In the text | |
 |
Fig. B.1. As in the right column of Fig. 4, but for rerr = 0, aerr = 0.1 mK and for ℓ ≤ 3. See legend. |
| In the text | |
 |
Fig. C.1. Comparison between the real space filter without and with prefiltering, the original case and the ideal, fully analytical case, starting from the analytical formulation of the ESMB for rerr = 2.5 × 10−3 and Smax = 0.1 Jy. See legend and text. |
| In the text | |
 |
Fig. C.2. As Fig. C.1 but without the original case, for rerr = 2.5 × 10−5 and for ℓ = 5 and 6. See legend. |
| In the text | |
 |
Fig. D.1. Comparison between the two favourite filters including (two bottom panels) or not including (two top panels) the prefiltering, the original case, and the ideal, fully analytical case for the EDGES profile for rerr = 10−2. See legend. |
| In the text | |
 |
Fig. D.2. As in Fig. D.1 but without the original case, for rerr = 10−4 at ℓ = 1 and 2 (left column) and at ℓ = 5 and 6 (right column). See legend. |
| In the text | |
 |
Fig. E.1. Percentage difference between Δa1, 0 computed for the analytical description of the EDGES absorption profile using Eq. (10) with all the terms and taking only the contribution from the first-order derivative, in the ideal case without errors. We note that the expected divergence at a frequency of around ≃73.5 MHz disappears only due to frequency sampling. Solid (dots) lines refer to positive (negative) values. See text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.







![$$ \begin{aligned} a_{\ell ,0}&= A_\ell \sqrt{\frac{4\pi }{2\ell +1}} \Bigg [d_{\ell ,1} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=1) + T_{\rm th}^\mathrm{BB/dist} ({ w}=-1)}\right)\nonumber \\&\quad + d_{\ell ,2} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=\sqrt{2}/2) + T_{\rm th}^\mathrm{BB/dist} ({ w}=-\sqrt{2}/2)}\right) \nonumber \\&\quad + d_{\ell ,3} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=1/2) + T_{\rm th}^\mathrm{BB/dist} ({ w}=-1/2)}\right) \nonumber \\&\quad + d_{\ell ,4} T_{\rm th}^\mathrm{BB/dist} ({ w}=0) \Bigg ] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq9.gif)
![$$ \begin{aligned} a_{\ell ,0}&= A_\ell \sqrt{\frac{4\pi }{2\ell +1}} \Bigg [d_{\ell ,1} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=1) - T_{\rm th}^\mathrm{BB/dist} ({ w}=-1)}\right)\nonumber \\&\quad + d_{\ell ,2} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=\sqrt{2}/2) - T_{\rm th}^\mathrm{BB/dist} ({ w}=-\sqrt{2}/2)}\right)\nonumber \\&\quad + d_{\ell ,3} \left({T_{\rm th}^\mathrm{BB/dist} ({ w}=1/2) - T_{\rm th}^\mathrm{BB/dist} ({ w}=-1/2)}\right)\Bigg ] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq10.gif)
![$$ \begin{aligned} a_{\ell ,0} =&2\, A_\ell \sqrt{\frac{4\pi }{2\ell +1}} \Bigg [\Bigg (d_{\ell ,1} + d_{\ell ,2} + d_{\ell ,3}\Bigg )\, T_{\rm th}^{(0)} \nonumber \\& + \frac{1}{2!} \,\Bigg (d_{\ell ,1} + \frac{1}{2} d_{\ell ,2} + \frac{1}{4} d_{\ell ,3}\Bigg )\, T_{\rm th}^{\prime \prime } \nonumber \\& + \frac{1}{4!} \,\Bigg (d_{\ell ,1} + \frac{1}{4} d_{\ell ,2} + \frac{1}{16} d_{\ell ,3}\Bigg )\, T_{\rm th}^{(4)} \nonumber \\& + \frac{1}{6!} \,\Bigg (d_{\ell ,1} + \frac{1}{8} d_{\ell ,2} + \frac{1}{64} d_{\ell ,3}\Bigg )\, T_{\rm th}^{(6)} + \frac{1}{2}\,d_{\ell ,4}\, T_{\rm th}^{(0)} \Bigg ] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq20.gif)
![$$ \begin{aligned} a_{\ell ,0}&= 2\, A_\ell \sqrt{\frac{4\pi }{2\ell +1}} \Bigg [\Bigg (d_{\ell ,1} + \frac{\sqrt{2}}{2}d_{\ell ,2} + \frac{1}{2}d_{\ell ,3}\Bigg )\, T_{\rm th}^{\prime } \nonumber \\&\quad + \frac{1}{3!}\,\Bigg (d_{\ell ,1} + \frac{\sqrt{2}}{4}d_{\ell ,2} + \frac{1}{8}d_{\ell ,3}\Bigg )\, T_{\rm th}^{\prime \prime \prime } \nonumber \\&\quad + \frac{1}{5!}\,\Bigg (d_{\ell ,1} + \frac{\sqrt{2}}{8}d_{\ell ,2} + \frac{1}{32} d_{\ell ,3}\Bigg )\, T_{\rm th}^{(5)} \Bigg ] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq21.gif)
![$$ \begin{aligned}&a_{0,0} = \sqrt{4\pi } \; \left[T_{\rm th}^{(0)} + \frac{1}{6} T_{\rm th}^{\prime \prime } + \frac{1}{120} T_{\rm th}^{(4)} + \frac{1}{5040} T_{\rm th}^{(6)} \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq22.gif)
![$$ \begin{aligned}&a_{1,0} = \sqrt{\frac{4\pi }{3}} \; \left[T_{\rm th}^{\prime } + \frac{1}{10} T_{\rm th}^{\prime \prime \prime } + \frac{1}{280} T_{\rm th}^{(5)} \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq23.gif)
![$$ \begin{aligned}&a_{2,0} = \frac{1}{3}\sqrt{\frac{4\pi }{5}} \; \left[T_{\rm th}^{\prime \prime } + \frac{1}{14} T_{\rm th}^{(4)} + \frac{1}{504} T_{\rm th}^{(6)} \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq24.gif)
![$$ \begin{aligned}&a_{3,0} = \frac{1}{15}\sqrt{\frac{4\pi }{7}} \; \left[T_{\rm th}^{\prime \prime \prime } + \frac{1}{18} T_{\rm th}^{(5)} \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq25.gif)
![$$ \begin{aligned}&a_{4,0} = \frac{1}{105}\sqrt{\frac{4\pi }{9}} \; \left[T_{\rm th}^{(4)} + \frac{1}{22} T_{\rm th}^{(6)} \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq26.gif)



![$$ \begin{aligned} \frac{\mathrm{d}T_{\rm th}^2}{\mathrm{d}{ w}^2}&= \frac{d}{\mathrm{d}{ w}} \left({\frac{\mathrm{d}T_{\rm th}}{\mathrm{d}{ w}}}\right) = \frac{-\beta \nu }{(1 - \beta ^2)^{1/2}} \left[{\frac{d}{\mathrm{d}\nu^\prime } \left({\frac{\mathrm{d}T_{\rm th}}{\mathrm{d}\nu^\prime }}\right)}\right] \frac{\mathrm{d}\nu^\prime }{\mathrm{d}{ w}}\\&= \frac{\mathrm{d}T_{\rm th}^2}{\mathrm{d}\nu ^{\prime 2}} \left[{\frac{-\beta \nu }{(1 - \beta ^2)^{1/2}}}\right]^2\,\nonumber \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq31.gif)
![$$ \begin{aligned} \frac{\mathrm{d}T_{\rm th}^n}{\mathrm{d}{ w}^n} = \frac{\mathrm{d}T_{\rm th}^n}{\mathrm{d}\nu ^{\prime n}} \left[{\frac{-\beta \nu }{(1 - \beta ^2)^{1/2}}}\right]^n. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq32.gif)



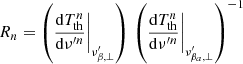



![$$ \begin{aligned} \mathrm{(i)}\;\; T_{\rm th}^\mathrm{BB/dist} (u_i) \rightarrow F(f_i)&= \mathrm{FFT} \left(T_{\rm th}^\mathrm{BB/dist} (u_i)\right)\nonumber \\ \mathrm{(ii)}\;\; F(f_i) \rightarrow F_{\rm s}(f_i)&= F(f_i) \left[\mathrm{e}^{-(f_i/\sigma _{\rm f})^2} + \mathrm{e}^{-((f_i-N_{\rm p})/\sigma _{\rm f})^2}\right]\\ \mathrm{(iii)}\;\; F_{\rm s}(f_i) \rightarrow T_{\rm th,s}^\mathrm{BB/dist} (u_i)&= \mathrm{Real} \left({\mathrm{FFT}^{-1} (F_{\rm s}(f_i))}\right), \nonumber \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq54.gif)
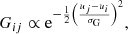
![$$ \begin{aligned} { w} = \mathrm{cos}\, \theta = \frac{1}{\beta } \left[{1 - (1-\beta ^2)^{1/2} \frac{\nu^\prime }{\nu }}\right]. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48335-23/aa48335-23-eq62.gif)



