EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 688 (August 2024) A&A, 688 (2024) A15 Full HTML
Open Access
Issue
A&A
Volume 688, August 2024
Article Number A15
Number of page(s) 24
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202450679
Published online 30 July 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Although extremely important for understanding the formation and evolution of planets, confirmed transiting exoplanets orbiting stars in stellar clusters and associations remain scarce. Only a few tens of planets have been found transiting stars younger than 100 Myr1 so far (e.g. David et al. 2016, 2019; Plavchan et al. 2020; Zakhozhay et al. 2022). Their detection is mainly hampered by the difficulties in observing transits in the light curves of stars located in dense stellar environments, such as star clusters, although in recent years several techniques have been developed that minimise the problems due to contamination of nearby stars and the number of false-positive detections (e.g. Nardiello et al. 2019, 2020, 2021; Battley et al. 2022). The stellar activity signals prevailing in the photometric and spectroscopic time series of young stars also make the detection and characterisation of exoplanets difficult, although huge progress has been made in the last few years in the development of techniques to disentangle and filter out stellar activity signals from those due to planetary companions.

The advantage of investigating stellar clusters and associations is that, by using theoretical or empirical models, it is possible to derive precise stellar parameters such as radius, mass, effective temperature, chemical content, and age of the cluster members. Consequently, this in principle allows us to measure the precise age, mass, and radius of the hosted exoplanets. At the same time, young stellar clusters offer the unique opportunity to investigate how the properties of the exoplanetary systems change with time immediately after their formation. Observing young systems at different ages is key to understanding the timing of the different physical processes occurring within the first ~100 Myr after planet formation, which heavily influence the physical properties and architectures that we observe in mature planetary systems. These processes include planet-disc interactions (e.g. Lin & Ida 2004), and planet-planet and planet-planetesimal interactions (e.g. Chatterjee et al. 2008; Nagasawa & Ida 2011). Other less catastrophic processes affecting young short-period planets include thermal contraction and atmospheric mass loss, which are driven either by core-powered mechanisms (e.g. Ginzburg et al. 2018; Gupta & Schlichting 2019) or photo-evaporation (e.g. Owen & Wu 2013; Lopez & Fortney 2013). In particular, photo-evaporation is most active within the first ~100 Myr, while core-powered mass loss acts over longer timescales.

The detection and characterisation of infant exoplanets will help constrain the timescales on which these mechanisms act, including planet migration and tidal orbital circularisation, where detailed knowledge of the environment where the systems formed is also of importance (e.g. stellar number density and radiation field). Obtaining accurate and precise radius and mass measurements – which in turn allow measurement of the planets’ bulk densities by combining photometric and radial velocity (RV) time series – is crucial to improve theoretical models of planetary formation and evolution at the earliest stages. In this regard, transiting young planetary systems, such as those detected by the NASA Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015), are particularly valuable, and they have been feeding most of the RV follow-up campaigns so far. However, young and, especially, infant stars show high levels of magnetic activity; this causes quasi-periodic RV variations of up to levels of hundreds of m s−1, which can severely dwarf planetary signals (see e.g. Damasso et al. 2020; Suárez Mascareño et al. 2021 as extreme examples). High levels of magnetic activity also hamper the detection and precise modelling of small-depth photometric transits. Significant progress has been made in optimising the whole analysis framework: testing different RV-extraction tools (e.g. methods based on the spectral cross-correlation function and template matching); using sophisticated methods to filter out stellar activity signals from RV time series (e.g. techniques based on Gaussian processes regression), jointly modeled with time series of spectroscopic activity diagnostics and photometric light curves; and improved methods for extracting and filtering light curves of young stars (e.g. Canocchi et al. 2023). Nonetheless, most young planets presently have upper limits on their mass, and masses have been measured for only a limited sample.

TOI-837 is an infant and very active solar-type star, a bona fide member of the young open cluster IC 2602, with an age of 35−5+11$35_{ - 5}^{ + 11}$ Myr and a metallicity of [Fe/H]=−0.069±0.042 (Bouma et al. 2020). A planet candidate, TOI-837.01 was discovered by TESS. The candidate was also identified in the independent analysis by Nardiello et al. (2020) and labelled PATHOS-30. The candidate, which has a orbital period of ~8.32 days and a Saturnlike size, was validated as a planet (then labelled as TOI-837 b) by Bouma et al. (2020), who determined a 3σ mass upper limit of 1.2 MJup.

To our knowledge, TOI-837 b is the youngest validated transiting planet known in an relatively young open cluster so far. It joined a small ensemble of transiting planets in young associations with well-known age, comprising AU Mic b and c in the β Pic moving group (see e.g. Plavchan et al. 2020; Martioli et al. 2021; Zicher et al. 2022); the multi-planet system V1298 Tau in the Taurus-Ext association (see e.g. David et al. 2019; Suárez Mascareño et al. 2021; Feinstein et al. 2022); HIP 67522 b (Rizzuto et al. 2020), HD114082b (Zakhozhay et al. 2022), K2-33 b (Mann et al. 2016; David et al. 2016), and TOI-1227 b (Mann et al. 2022) in the Sco-Cen group; and DS Tuc Ab in the Tuc-Hor association (Benatti et al. 2019; Newton et al. 2019). The measurement of mass through RV monitoring is of special interest, firstly for final confirmation of the planetary nature of the stellar companion, but especially for inference of its bulk density, internal and atmospheric structure, and for studying its formation and evolutionary history at early ages. The identification of the planet’s Doppler signature in the RVs would also allow the characterisation of the orbit of TOI-837 b, providing insights into the formation and migration pathway at such a young age within a crowded environment, which is potentially favourable to the production of dynamical perturbations.

In this paper, we present an updated analysis and characterisation of the system based on photometric data that include recent TESS sectors and archival HARPS high-resolution spectra (Sect. 2). Fundamental stellar parameters are presented in Sect. 3, while in Sect. 4 we discuss the analysis of the photometric and spectroscopic data, including the modeling of the dominant signals due to stellar magnetic activity. The implications of a significant detection of the RV Doppler signal and – consequently – of the mass measurement of TOI-837 b for the formation and atmospheric evolution history of the system are discussed in Sect. 5, where we also present interesting perspectives for a follow-up with James Webb Space Telescope (JWST) to characterise the atmospheric composition of the planet.

We point out that, while our analysis was in progress, a parallel study of TOI-837 was submitted and posted online as a pre-print (Barragán et al. 2024). We emphasise that our results were not influenced by those of Barragán et al. (2024). Our study should be considered as an independent and alternative work, although it is based on the same HARPS and TESS raw data.

2 Description of the datasets

2.1 Photometry

TOI-837 was observed by TESS in Sectors 10 and 11 (between 26 March and 21 May 2019), in Sectors 37 and 38 (between 2 April and 26 May 2021), and in Sectors 63 and 64 (between 10 March and 6 April 2023), spanning 749.3 days. We extracted the light curves from the short-cadence data using the PATHOS pipeline described in Nardiello et al. (2019, 2020, 2021). We corrected the light curves by adopting cotrending basis vectors for short-cadence data obtained and applied as described by Nardiello (2020). We did not make use of the PDCSAP (Smith et al. 2012; Stumpe et al. 2012, 2014) light curves because for this kind of highly variable star they are usually affected by systematic errors due to over-corrections in the official TESS pipeline (see Nardiello et al. 2022 for details). Figure 1 shows the TESS field of view centred on TOI-837, revealing the presence of several photometric contaminants falling within the TESS aperture that contains the target, identified from Gaia DR3 following the methodology outlined in Mantovan et al. (2022). The stars nearby to TOI-837 and blended with it are accounted for to calculate the dilution factor, which is defined as the total flux from contaminant stars that fall into the photometric aperture divided by the flux of the target star. The dilution factor is used to correct the depth of the transit signal and, consequently, to provide a corrected measurement of the planet radius. For the case of TOI-837, we derived a significant dilution factor of 0.178±0.005.

We detrended the light curve using the cosine estimator implemented in the wōtan package (Hippke et al. 2019) with a window length of 0.25 days, and masking the transits using the ephemeris reported by Bouma et al. (2020). Figure 2 shows the light curve together with the model adopted for the flattening of the time series, and the flattened light curve.

thumbnail Fig. 1

Gαiα DR3 stars identified in the TESS field of view of TOI-837, which is identified by the letter ‘t’. Several stellar contaminants fall within the TESS aperture. Δm denotes the magnitude difference in the Gaia G-band between each field star and TOI-837.

2.2 Spectroscopy

We downloaded 78 public HARPS spectra from the European Southern Observatory (ESO) archive, processed with the standard Data Reduction Software (DRS) v3.8 (template mask G2). The spectra were collected within program ID 110.241K.001/0110.C-4341(A) (Precise masses of very young transiting planets with HARPS; PI Yu). We discarded two spectra at epochs BJD 2459858.875731 and 2459880.857826, which, based on the information in the fits header, very likely correspond to a different source. For our analysis, we selected spectra with a signal-to-noise ratio (S /N) > 25, measured at the echelle order 50 (~5700 Å), resulting in 70 good epochs covering a time span of 101 days. The exposure times are 900 s and 1800 s. Data are provided in Table A.1. The star is a fast rotator (v sin i⋆ ~ 16 km s−1), and the archival RVs calculated by default from the DRS cross-correlation function (CCF) are not trustworthy because of the narrow half-window used to calculate the CCF. Therefore, we did not analyse the DRS RVs in this study, but instead extracted the RVs using the Python-based code SERVAL (spectrum radial velocity analyser, version dated on 26 January 2022; Zechmeister et al. 2018), which adopts a procedure based on template-matching to derive relative RVs2. The resulting RV time series is characterised by an RMS of 112 m s−1 and median internal error σRV = 10.2 m s−1.

3 Stellar characterisation

3.1 Fundamental stellar parameters

We derived the effective temperature (Teff), surface gravity (log g), and iron abundance ([Fe/H]) by applying the spectral synthesis method to the co-added spectrum of the target. In particular, we used the spectral analysis tool iSpec (Blanco-Cuaresma et al. 2014, Blanco-Cuaresma 2019) to measure these parameters. Specifically, we considered the sixth version of the GES atomic line list (Heiter et al. 2021), both the MOOG (Sneden 1973, version 2019) and SME (Valenti & Piskunov 1996, version 4.23) radiative transfer codes, and the MARCS (Gustafsson et al. 2008) and ATLAS9 (Castelli & Kurucz 2003) grids of model atmospheres, obtaining consistent results. Regions encompassing the wing segments of the Hα, Hβ, and Mg I triplet lines together with Fe I and Fe II lines in the 476–678 nm spectral region were considered to constrain parameters. We then employed the non-linear least-squares Levenberg-Marquardt fitting algorithm (Markwardt 2009) to iteratively minimise the χ2 value between the synthetic and observed spectra. Final mean values of the derived spectroscopic atmospheric parameters are listed in Table 1. As by-products, we also derived the projected rotational velocity (υ sini⋆) macrotur-bulence and microturbulence velocity (Vmacro, Vmicro). We also measured Teff considering the line-depth ratio (LDR) method and appropriate LDR–Teff calibrations developed at the same resolution as HARPS-N (see Biazzo et al. 2011), obtaining similar results within the uncertainties.

To determine the stellar physical parameters, namely mass, radius, and age, we simultaneously modelled the stellar spectral energy distribution (SED; see Table 1 for the magnitudes used, and Fig. 3) and the MIST stellar evolutionary tracks (Paxton et al. 2015) through a Bayesian differential evolution Markov chain Monte Carlo framework with the EXOFASTv2 tool (Eastman 2017; Eastman et al. 2019). We imposed Gaussian priors on the previously derived Teff and [Fe/H], the Gaia DR3 parallax, and the stellar age 𝒩(35, 15) Myr. We also employed the PARSEC (Bressan et al. 2012) stellar models instead of the MIST ones, and found almost equal stellar parameters and uncertainties. The derived stellar parameters are given in Table 1. All stellar parameters derived by our analysis are in agreement with those reported by Bouma et al. (2020) within less than 1σ.

Finally, we measured the equivalent width of the Li line at ~6707.8 Å together with the Li abundance corrected for non-local thermodynamic equilibrium (NLTE) effects (Lind et al. 2009). Their values, namely EWLi = 169 ± 6 mÅ and logA(Li)NLTE = 3.18 ± 0.04 dex, are compatible with the membership of TOI-837 to the IC 2602 young open cluster (see e.g. Sestito & Randich 2005; Jeffries et al. 2023).

Figure 4 shows the Gaia DR3 colour–magnitude diagram of IC 2602 members with a 35 Myr BASTI-IAC isochrone3 superimposed (Hidalgo et al. 2018; Pietrinferni et al. 2021). The star is located on the main sequence of the cluster and shares the same proper motion and parallax. The isochrone fitting suggests TOI-837 has a mass of about 1.12 M⊙, a solar radius, and a Teff ~ 6040 K, in agreement with the spectroscopic stellar parameters adopted in this work.

3.2 A stellar companion at wide separation

A star at about 2.3″ from TOI-837 (namely TIC 847769574) was previously mentioned by Bouma et al. (2020). These authors reported a similar parallax and proper motion to that given in Gaia DR2, but slightly discrepant values for the distance, inferring that this object is a member of the IC 2602 open cluster but is not physically bound to TOI-837. We reconsider the physical association of the two stars exploiting Gaia DR3 astrometry. Their parallaxes are now compatible at l.6σ- level. Therefore, the argument of different distances no longer applies. Proper motion differs by a significant amount in declination (2.0 mas yr−1), while it agrees within the error bars in terms of right ascension. This difference corresponds to a velocity difference of about 1.33 km s−1 at the distance of TOI-837. This is fully compatible with orbital motion in a bound pair with a separation of ~330 au. From the density of targets observed around TOI-837 with astrometric properties compatible with cluster membership in Gaia DR3, a low probability of the order of 0.1% is derived for catching another cluster object at a projected separation of as small as 2.3″. We conclude that the characteristics of the object found at close separation from TOI-837 are fully compatible with those of a gravitationally bound object, and that the presence of an unbound cluster member projected at such close separation is very unlikely. We estimate M = 0.33 M⊙ for the mass of the stellar companion using the stellar models by Baraffe et al. (2015). With a magnitude difference of 4.91 in Gaia G-band and a larger difference in V-band, the impact of the bound companion on the time variations of the RV data of TOI-837 discussed below is expected to be negligible.

thumbnail Fig. 2

Short-cadence lightcurves of TOI-837 observed by TESS in Sectors 10 and 11 (top panel), 37 and 38 (middle panel), and 63 and 64 (bottom panel). For each pair of sectors, we report the short-cadence light curve and the detrending model (in azure), and the corresponding flattened light curve. The transits of TOI-837 b are indicated with red triangles.
thumbnail Fig. 3

Spectral energy distribution of TOI-837 with the best-fit model over-plotted (solid line). Red and blue points correspond to the observed and predicted values, respectively.
Table 1

Stellar parameters of TOI-837 (CPD-63 1435).

4 Data analysis

4.1 Photometric stellar rotation period

We performed a Gaussian process (GP) regression analysis to model each pair of TESS sectors individually, with the goal being to measure the stellar rotation period Prot,⋆, and to characterise the evolutionary timescales of the periodic variations as seen in the light curve. We adopted the GP quasi-periodic (QP) kernel, whose covariance matrix is defined as (e.g. Haywood et al. 2014) kQP(t,t′)=h2⋅exp[ −(t−t′)22λ2−sin2(π(t−t′)/θ)2w2 ] +(σ2(t)+σjit2)⋅δt,t′,$\eqalign{ & {k_{{\rm{QP}}}}\left( {t,{t^\prime }} \right) = {h^2} \cdot \exp \left[ { - {{{{\left( {t - {t^\prime }} \right)}^2}} \over {2{\lambda ^2}}} - {{{{\sin }^2}\left( {\pi \left( {t - {t^\prime }} \right)/\theta } \right)} \over {2{w^2}}}} \right] \cr & & + \left( {{\sigma ^2}(t) + \sigma _{{\rm{jit}}}^2} \right) \cdot {\delta _{t,{t^\prime }}}, \cr} $(1)

where t and ť′are two different epochs of observations; σ(t) is the uncertainty of a data point at epoch t; δt,t′ is the Kronecker delta; and σjit is a constant jitter term added in quadrature to the formal uncertainties σ(t) to account for other sources of uncorrelated noise. The GP hyper-parameters are h, which denotes the scale amplitude of the correlated signal (uniform prior: 𝒰(0,5) days); θ, which corresponds to the stellar rotation period Prot,⋆ (uniform prior: 𝒰(0,l) days); w, which describes the harmonic complexity of the rotation period within a complete stellar rotation cycle (uniform prior: 𝒰(0,l) days); and λ, which represents the decay timescale of the correlations, and is related to the temporal evolution of the magnetically active regions (uniform prior: 𝒰(0,1000) days). We included a linear trend in the model for sectors 63 and 64. To perform the GP regression, we used the publicly available PYTHON module GEORGE v0.2.1 (Ambikasaran et al. 2015). We explored the full parameter space using the Monte Carlo (MC) nested sampler MultiNest v3.10 (e.g. Feroz et al. 2019) through the pyMultiNest wrapper (Buchner et al. 2014). The weighted mean for Prot,⋆ from the three measurements is 2.973±0.006 days. For the λ hyper-parameter, the weighted mean is 4.83±0.05 days, implying the presence of active regions that evolve quickly on a timescale of shorter than two rotation cycles.

thumbnail Fig. 4

Proper motions and colour-magnitude diagram of the members of the open cluster IC 2602. Top panel shows the proper motions of the cluster members (in black) after a selection based on the parallax and the proper motions themselves. Bottom panel shows the Gaia G-mag versus BP-RP colour–magnitude diagram of the same stars with a BASTI-IAC isochrone of 35 Myr superimposed. In both panels, green symbols represent the target of this study.

4.2 Frequency content of radial velocities and spectroscopic activity diagnostics

Figure 5 shows the RV time series and the corresponding generalised Lomb-Scargle (GLS; Zechmeister & Kürster 2009) periodogram. A very significant peak is found at the stellar rotation period Prot,⋆, showing that the observed RV scatter is mainly due to activity. Interestingly, the periodogram of the prewhitened data (i.e. after removing the best-fit sinusoid calculated by GLS) shows a peak very close to the orbital period of planet b.

We analysed the time series of spectroscopic activity diagnostics, which can be used to disentagle planetary signals identified in the RVs from those due to stellar activity (Table A.2). Using the code ACTIN2 (Gomes da Silva et al. 2018, 2021), we calculated the chromospheric activity index SMW derived from the CaII H&K line doublet and calibrated to the Mount Wilson scale following Gomes da Silva et al. (2021), and the activity diagnostic derived from the H-alpha line. Additionally, we calculated the activity diagnostics differential line width (DLW) and the chromatic index (CRX) using SERVAL (Zechmeister et al. 2018). DLW is equivalent to the full-width at half maximum of the spectral cross-correlation function, and the CRX, which is defined as the slope of the plot of RV versus the logarithm of the wavelengths of the individual echelle orders, allows us to investigate the extent to which the RVs are ‘chromatic’ due to the effects of activity. Time series and periodograms are shown in Fig. 6. The SMW-index shows a long-term modulation, for which it is not possible to determine a periodicity because of the limited time span of the data. After correcting the data by fitting a quadratic trend, the GLS periodogram of the residual time series shows a main peak at 3.1 days. After prewhitening the residuals (i.e. removing a sinusoid with a period of 3.1 days), the periodogram of the new residual time series has a main peak at 2.99 days. The time series of the H-alpha index does not show a long-term trend, but the periodogram shows similarities with that of the prewhitened SMW-index; it shows two peaks close to the photometric Prot,⋆, with the one with higher power at 3.1 days. The periodogram of the prewhitened data has a main peak at 2.95 days. Our conclusion from the analysis of the S MW and H-alpha indexes is that there are two distinct sinusoidal-like signals with periodicities very close to the photometric Prot,⋆, possibly indicative of differential rotation. The DLW time series shows a clear long-term modulation with a significant GLS periodicity of ∽81 days. The periodogram of the prewhitened time series shows a single peak related to Prot,⋆. The periodogram of the CRX index is dominated by a single peak related to Prot,⋆, while that of the prewhitened CRX data shows a peak at ∽70 days. Thus, the frequency analysis of both the DLW and CRX indexes reveals the presence of a modulation over a timescale much longer than the rotation period.

We employed the Python code pyrhk4 to convert the values of the SMW index to the standard logRHK′$\log R_{{\rm{HK}}}^\prime $ chromo-spheric emission ratio using the standard formula proposed by Noyes et al. (1984), and bolometric correction taken from Middelkoop (1982). We obtained logRHK′=−4.311±0.018$\log R_{{\rm{HK}}}^\prime = - 4.311 \pm 0.018$. This measurement was employed to also estimate the coronal X-ray luminosity of TOI-837, which we need in order to study the photo-evaporation history of the planet (Sect. 5.2).

thumbnail Fig. 5

Time series and periodogram of the HARPS RVs. Upper panel: RV time series of TOI-837 (SERVAL extraction). Middle panel: GLS periodogram of the original and prewhitened data. False-alarm probability levels for the periodogram of the original RV dataset are indicated by horizontal dashed lines. Lower panel: window function of the data.

4.3 Radial velocity and photometry joint analysis

We performed a RV and photometry joint analysis to derive orbital and physical parameters of TOI-837 b, and search for undetected companions. From the detrended light curve, we removed data points corresponding to the flares clearly visible in Fig. 2.

The MC MultiNest setup for the joint RV and photometric analysis included 500 live points, a sampling efficiency of 0.3, and a Bayesian evidence tolerance of 0.5. We used the code batman (Kreidberg 2015) to model the photometric transits. Concerning the light-curve modelling, we used the stellar density ρ* as a free parameter from which we derived the ab/R⋆ ratios at each step of the MC sampling (e.g. Sozzetti et al. 2007) using a Gaussian prior based on the mass and radius derived in Sect. 3. We adopted a quadratic law for the limb darkening, and fitted the coefficients u1 and u2 using the parametrisation and the uniform priors for the coefficients q1 and q2 given by Kipping (2010) (see Eqs. (15) and (16) therein). We also introduced a constant jitter σjit added in quadrature to the nominal photometric uncertainties.

Concerning the fit of the RVs, we considered a base model that includes a Keplerian to fit the Doppler signal of the transiting planet – either keeping the eccentricity eb as a free parameter, or fixing eb = 0 −, an offset γRV, and a secular acceleration γ˙$\dot \gamma $. The dominant signal due to the stellar activity, which is modulated over Prot,⋆, was modelled using a GP regression, adopting the quasi-periodic kernel of Eq. (1). For the base model, we found that assuming a circular orbit for TOI-837 b is statistically favoured over the eccentric case, and we adopt eb = 0 for the rest of our analysis. More complex RV models were tested to search for additional significant signals present in the dataset and possibly ascribable to planetary companions. Periods of the additional signals were sampled uniformly either in the range of 10 to 100 days or below 7 days. We find that the best-fit model for our RV data includes a sinusoid to fit a signal with a period of longer than the orbital period Pb of TOI-837 b, and a second GP quasi-periodic kernel, which is added to the first kernel to fit a third signal with a period of shorter than Pb. This model is statistically strongly favoured over the base model, with Δ ln 𝒵3signals–1planet = +6.0, where 𝒵 denotes the Bayesian evidence calculated by MultiNest. We adopt this as our reference model. Priors and results for both the base and adopted model are summarised in Table 2, where the parameters of the long-period sinusoid are labelled with the subscript ‘long-period’, while the hyperparameters of the second GP quasi-periodic signal are labelled with the subscript ‘2’. The posteriors are shown in the corner plot of Fig. A.1. We provide a description and interpretation of the results in the following. The most relevant plots are shown in Figs. 7 and 8 for the RVs and photometry, respectively.

Analysing the results for the RVs, the Doppler signal due to TOI-837 b is robustly detected (Kb=34.2−5.3+4.9 m s−1${K_{\rm{b}}} = 34.2_{ - 5.3}^{ + 4.9}{\rm{m}}{{\rm{s}}^{ - 1}}$, ~6.5σ significance level), and translates into a true mass of mb=116−18+17M⊕${m_{\rm{b}}} = 116_{ - 18}^{ + 17}{M_ \oplus }$ when taking into account the measured orbital inclination angle of ib=86.96±0.05 degrees from the transit photometry. The sum of two GP quasi-periodic kernels is able to effectively filter out a correlated signal linked to Prot,⋆. 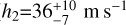This activity-related signal is composed of a dominant component (h1=181−58+68 m s−1${{h_1} = 181_{ - 58}^{ + 68}{\rm{m}}{{\rm{s}}^{ - 1}}}$) with a well-constrained period of θ1=3.000−0.004+0.003${\theta _1} = 3.000_{ - 0.004}^{ + 0.003}$ days and a secondary component (h2=36−7+10 m s−1${h_2} = 36_{ - 7}^{ + 10}{\rm{m}}{{\rm{s}}^{ - 1}}$) with a period of θ2=3.06−0.28+0.25 ${\theta _2} = 3.06_{ - 0.28}^{ + 0.25}{\rm{ }}$ days and a shorter evolutionary timescale (λ2=6−3+16 days ${\lambda _2} = 6_{ - 3}^{ + 16}{\rm{ days }}$), which is similar to the values measured for the λ hyperparameter from the TESS light curve (Sect. 4.1). We find evidence in the periodogram of the SMW and H-alpha activity indicators for a similar bimodal periodicity related to Prot,⋆ (Sect. 4.2), which supports the use of a sum of two quasi-periodic kernels. The second long-period sinusoid included in our best-fit model is significant (semi-amplitude Klong period =42.6−12.2+11.2 m s−1${K_{{\rm{long period }}}} = 42.6_{ - 12.2}^{ + 11.2}{\rm{m}}{{\rm{s}}^{ - 1}}$), with a periodicity of Plong period =74.8−9.1+13.4${P_{{\rm{long period }}}} = 74.8_{ - 9.1}^{ + 13.4}$ days. This signal is very unlikely to be due to a second companion in the system, and appears related to stellar activity; although the interpretation of the physical mechanism responsible for this activity is not straightforward. A high positive correlation exists between this long-period RV signal and the prewhitened CRX index (i.e. after removing the signal due to stellar rotation; Fig. A.2), with a correlation coefficient of ρPearson=+0.71. An RV Doppler shift induced by a planet is achromatic; that is, its properties are independent of the wavelength of the stellar spectral lines, while an anti-correlation with the CRX is observed for RV signals that are related to spot-dominated stellar activity (Zechmeister et al. 2018). The observed positive correlation for TOI-837 does not have an immediate astrophysi-cal explanation, but it prevents us from interpreting the RV signal as due to an additional companion in the system. We note that the values of the parameters of planet TOI-837b are in agreement within the error bars for the two models shown in Table 2. This means that the characterisation of planet b is not affected by a more complex modelling of the activity-related signals in the RV time series, although this complexity is required by the data.

The best-fit model for the light curve (Fig. 8) corresponds to a grazing transit (impact parameter b=0.91±0.02) and to a planetary radius of rb=9.71−0.60+0.93R⊕${r_{\rm{b}}} = 9.71_{ - 0.60}^{ + 0.93}{R_ \oplus }$. Our measured mass and radius imply a most-likely Saturn-like bulk density for TOI-837 b, of 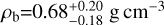ρb=0.68−0.18+0.20 g cm−3${\rho _{\rm{b}}} = 0.68_{ - 0.18}^{ + 0.20}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$(ρsat=0.687 g cm−3).

As a final note, we find that running TLS on the TESS light curve after masking the transits of planet TOI-837 b does not result in a significant detection of additional signals.

Table 2

Priors and best-fit values of the free and derived parameters related to the joint RV+light curve modelling.

thumbnail Fig. 6

Time series and periodogram of spectroscopic activity diagnostics calculated from HARPS spectra. Left pαnel: time series (black dots) of activity diagnostics extracted from HARPS spectra. Right panel: GLS periodograms of the time series, and prewhitened time series, shown in the left panel. The vertical green line identifies the stellar rotation period measured from the TESS light curve.
thumbnail Fig. 7

Best-fit models related to the RV dataset obtained from the joint RV+light curve analysis described in Sect. 4.3. First row: RV time series with the adopted best-fit model over-plotted (red curve; activity plus Doppler signal due to TOI-837 b). Second row: phase-folded Doppler RV signal of TOI-837 due to planet b (left panel), and the signal with a period of ∽ 74 days, which we interpret as due to stellar activity (right panel). Nominal error bars are indicated in black, while the error bars with an uncorrelated jitter term added in quadrature are indicated in green. Third row: stellar-activity-correlated signal in the RV time series (red dots) as fitted by a GP regression including the sum of two quasi-periodic kernels. The blue line represents the best-fit model, and the 1σ confidence interval is shown as a shaded grey area. The panel on the right is a zoomed-in view of the left panel, for better readability. To calculate all the theoretical curves shown here, we adopted the median values of the model parameters in Table 2.
thumbnail Fig. 8

Phase-folded transit light curve of TOI-837 b, and O–C residuals. The data point on the bottom right of the first panel shows the median error bar of the complete photometric time series.

5 Discussion

Figure 9 shows the mass-radius diagram for transiting planets younger than 200 Myr discovered so far, showing those with measured masses (black circles) and those for which only upper limits on mass are available (black triangles)5. Their number is still too scarce to allow demographics of infant and adolescent planets compared to mature planets (which are identified with grey dots in the plot), and therefore it is important to increase the number of detections in the future and to provide robust constraints on the planetary masses in an attempt to overcome the limits imposed by stellar activity. This is essential to confirm whether or not highly irradiated, very young exoplanets show larger radii with respect to the mature counterpart with a similar mass, as both theory (e.g. Linder et al. 2019; Owen 2020) and some observations currently suggest (e.g. Berger et al. 2020; Benatti et al. 2021; Mann et al. 2022). If so, in general, we should expect infant and adolescent planets to follow evolutionary tracks on the mass-radius diagram as they age. We investigate the evolution of TOI-837b on the mass–radius diagram in Sect. 5.2.

In the context of the known exoplanet population younger than 200 Myr, TOI-837 b joins a very small number of warm and hot giant-sized planets with a measured mass, which includes HD 114082 b (Zakhozhay et al. 2022) and Qatar-4b (Alsubai et al. 2017), with the exception of the 17 Myr old HIP 67522 b, for which only an upper limit on mass is available at present (Rizzuto et al. 2020). The detection of short-period transiting Saturn- and Jupiter-sized planets around very young stars should not be greatly hampered by stellar activity (although the accuracy and precision of the radius measurements can be affected), and therefore the impact of observational biases on the observed scarcity should be mild. If the investigation of a larger sample of young stars were to confirm that the low occurrence rate is real, this would greatly help to constrain the timescales of disc-migration mechanisms for massive planets.

In Fig. 9, we highlight the planet DS Tuc A b (Benatti et al. 2019, 2021) with a red triangle, because this system shares interesting similarities with TOI-837, which possibly justify a dedicated comparative study in the future. DS Tuc A is coeval with TOI-837, but has a later spectral type, being a 40±5 Myr old G6V main component of a binary system. It has a rotation period and activity level detected in the RVs, which are very close to those of TOI-837, and it hosts a planet with a similar semi-major axis (~0.08 au). The radius of DS Tuc Ab is about 0.5 RJup, but so far only a conservative upper limit on mass of 14.4 M⊕ has been derived from a RV time series measured from HARPS spectra (Benatti et al. 2019, 2021). DS Tuc Ab is therefore very likely an inflated super-Earth, at least one order of magnitude less massive than TOI-837b. It is possible that future RV follow-up studies will further constrain the mass, and allow characterisation of the internal structure and composition of DS Tuc A b. If the two planets share a similar formation history within protoplanetary discs with similar properties, the characterisation of DS Tuc A b might help to effectively reconstruct the formation history of TOI-837b. In the following, we present a preliminary investigation of the formation and evolutionary history of TOI-837b based on our measured planet’s parameters, population synthesis simulations, and models of mass-loss through photo-evaporation.

5.1 Formation history

We first estimated the timescale of tidal circularisation of the TOI-837 b orbit for a hypothetical eccentricity of eb = 0.15 from Eq. (1) in Matsumura et al. (2008) by assuming a modified tidal quality factor of Qp′=Q⋆′~106$Q_{\rm{p}}^\prime = Q_ \star ^\prime \~{10^6}$ (Bonomo et al. 2017) for both the host star and the planet as well as planet spin-orbit synchronisation. We find an orbit circularisation timescale close to the age of the Universe. Therefore, the circular orbit observed for TOI-837 b is very likely primordial, and indicates that the planet has undergone a smooth disc migration, with no excitation of its eccentricity.

Building on this indication, we explored the possible formation tracks of the planet in the framework of the pebble accretion scenario using our Monte Carlo implementation of the Planet Growth and Migration (GroMiT) code6. GroMiT uses the planetary core growth and migration treatments from Johansen et al. (2019), the pebble-isolation-mass scaling law from Bitsch et al. (2018), the gas accretion, gap-opening, and gap-driven migration treatments from Tanaka et al. (2020), and incorporates the condensation sequence treatment in protoplanetary discs from Turrini et al. (2023) to track the formation history of a planet from its original seed and formation region to its final mass and orbit based on the characteristics of its native circumstellar disc.

We consider a circumstellar disc with a total mass of 0.06 M⊙, characteristic radius of 50 au, gas surface density at the characteristic radius of 4.2 g cm−2, temperature profile defined as T = T0 • r−0.5, and a temperature T0 at 1au of 200 K (see Table 3 and Mantovan et al. 2024 for more details). In the population synthesis simulations with GroMίT, we considered both millimetre(mm)-sized and centimetre(cm)-sized pebbles, performing 105 Monte Carlo extractions for each pebble size. As shown in the left-hand panel of Fig. 10, the characteristics of the planet are reproduced with both selected pebble sizes. The major difference between the two populations is that in the case of mm-sized pebbles, the planetary seed must form within the first 2 Myr of the disc lifetime to successfully grow to the mass of TOI-837 b. In the case of the disc populated with cm-sized pebbles, on the other hand, the planetary seeds need to appear after 2.5 Myr of the disc lifetime to produce equivalent planets, otherwise the greater pebble size results in growth to larger masses. As discussed below, in our template disc, the planets that form in the innermost few astronomical units (au) from the star are characterised by small pebble isolation masses. This translates into long envelope contraction times that delay the onset of the runaway gas-accretion phase, limiting their final masses to a few earth masses. Planets that fulfil the conditions for entering the runaway gas growth phase can easily become more massive than TOI-837 b or migrate to the inner edge of the disc. As a consequence, the mass range between 3 and 100 M⊕ is sparsely populated near the orbital location of TOI-837 b.

The right-hand panel of Fig. 10 shows the resulting population of synthetic planets plotted in the semimajor orbit versus planetary mass parameter space, specifically zooming onto the planets with a final semimajor axis inwards of 4 au. The solutions we find within this uncertainty region all point to the original seed having originated from a position between 2 and 4 au from the parent star. As illustrated in Fig. 11, the core mass values of the compatible solutions are set by the pebble isolation mass to about 2 M⊕, with the onset of the runaway gas accretion occurring at a fraction of an au. Due to the range of possible formation distances of the planetary seed emerging from the population synthesis, both rock+metal cores and ice+rock mixtures are possible for the planetary core, although ice likely provides a limited fraction of the core mass in the latter case.

To gain further insight into the formation history of TOI-837 b, we coupled the population synthesis study with an investigation of the possible interior structures compatible with the planetary radius and mass emerging from the retrievals. To this end, we performed a Monte Carlo study based on the equations for the core and envelope radii from Lopez & Fort-ney (2014). We explored both solutions for both the solar opacity and enhanced opacity cases from Lopez & Fortney (2014), which are associated with faster and slower contraction timescales, respectively. We performed 106 MC runs, where we extracted the stellar age and the planetary mass from the posterior distributions emerging from the retrievals using normal distributions truncated to zero, and the core mass fraction from a uniform distribution between 0 and 1. We used the resulting values to compute the planetary radius using Eqs. (2) and (4) from Lopez & Fortney (2014), selecting only those combinations of values producing planetary radii, masses, and densities compatible within 3σ with the modal values from the retrievals.

The resulting distributions of compatible interior structures are shown in Fig. 12. As can be immediately seen, the slower contraction associated with envelopes with enhanced opacity strongly favours large cores with masses systematically greater than 30 M⊕ and generally well in excess of 50–60 M⊕ (see also Fig. 13). Solutions with smaller cores are sparse and are associated with planetary radii that are more than 2σ larger than the modal value (see Fig. 12). The faster contraction associated with envelopes of standard opacity allows instead for a second family of solutions with smaller core masses (Fig. 12). This second family of solutions spans cores of the order of that estimated for Saturn by gravity and ring seismology investigations (about 20 M⊕, Mankovich & Fuller 2021) to those with very small cores (sub-Earth mass). Overall, we find that about 31–32% of the solutions shown in Fig. 12 for the cases of standard opacity are synthetic planets with radius, mass, and density within 1σ of the retrieved best-fit values for TOI-837 b, and about one in six of these solutions (i.e. 5–6% of the total) have a core mass of below 25 M⊕.

Before moving further, it should be emphasised that these solutions are obtained for the standard and enhanced opacity cases from Lopez & Fortney (2014), which refer to envelopes with solar metallicity or 50× solar metallicity, respectively. Envelope compositions intermediate between these two end-member cases, like that of Saturn (Atreya et al. 2018), are not necessarily accurately fitted by these models. Further studies with more refined interior models are required before we can precisely assess the likelihood of Saturn-like or smaller cores. Notwithstanding this limitation, the relative frequency of solutions with Saturn-like or smaller cores in our Monte Carlo study does not allow us to discard this possibility a priori.

While our pebble-accretion simulations appear to point to core masses smaller than that estimated for Saturn (Mankovich & Fuller 2021), those core masses are actually lower limits set only by the pebble isolation mass profile of the disc. Two processes that are not included in the population synthesis study can increase the final core mass of the planet and allow for Saturn-like interior structures of TOI-837 b. First, the native pro-toplanetary disc of TOI-837 b could have been characterised by the presence of both pebbles and planetesimals at the time the giant planet formed. The accretion of planetesimals by TOI-837 b during its growth and migration would allow the core to grow beyond the pebble-isolation mass and would enrich the envelope in heavy elements (Shibata et al. 2020; Turrini et al. 2021).

Second, in a pebble-dominated disc, the volatile elements are expected to sublimate from the drifting pebbles and enrich the disc gas in the orbital regions inward of the snowlines (Booth & Ilee 2019). The accretion of such enriched gas would increase the budget of heavy elements of the giant planet and, if these heavy elements were to concentrate in the inner envelope, this accretion would mimic the effects of a larger, diluted core like those suggested by interior studies of Jupiter (Wahl et al. 2017; Stevenson 2020) and Saturn (Mankovich & Fuller 2021).

While they can produce similar effects on the interior structure of the giant planet, these two processes have different compositional implications that can be used to further probe the formation history and interior structure of TOI-837 b through the atmospheric characterisation of its refractory-to-volatile ratio. Specifically, planetesimal accretion is more effective in enriching the giant planet in refractory elements, while pebble accretion is more effective in enriching it in volatile elements (Türrini et al. 2021; Schneider & Bitsch 2021; Pacetti et al. 2022; Crossfield 2023). Consequently, if the giant planet formed in a pebble-dominated disc, its atmosphere should show significant enrichment in C, O, and N and limited or no enrichment in refractory elements. If the giant planets formed in a planetesimal-rich disc, due to its relatively high equilibrium temperature, its atmospheres should show greater enrichment in, for example, Na, K, and S than in C, O, and N.

thumbnail Fig. 9

Mass–radius diagram for a comparison between planets younger than 200 Myr and a mature population, and for assessing the prospects for a follow-up of TOI-837 b with JWST. Upper panel: mass-radius diagrams showing transiting planets with ages of less than 200 Myr (black symbols), taking the upper uncertainties on age into account for the definition of the age bin. Black dots indicate planets with a measured mass, while black triangles represent planets for which only an upper limit on mass is available. Grey dots represent a sample of older planets for which masses and radii have been measured with a precision of at least 30% and 10%, respectively. The current location of the planet TOI-837 b is indicated with a red dot, while the red asterisk and cross symbols denote the expected locations at an age of 1 Gyr for the cases of rock-ice core+low atmospheric opacity and rock-iron core+high atmospheric opacity, respectively (see Table 4 and Sect. 5.2 for details). A red triangle indicates the location of the planet DS Tuc Ab (1σ mass upper limit; Benatti et al. 2021). Saturn is identified by a blue dot. Diagonal dashed lines indicate the locations of planets with an equal density. Lower panel: mass–radius diagram of planets younger than 200 Myr, with dot size representing the TSM metrics for prospects of spectro-scopic follow-up with JWST. The mass of the planets is shown on a logarithmic scale. The giant planets (Rp > 8 R⊕ and Mp > 0.1 MJ) are represented within the light green area.
Table 3

Input parameters used to run the MC modified GroMiT code to produce simulated planets and investigate the formation history of TOI-837b.

thumbnail Fig. 10

Synthetic planetary populations resulting from the Monte Carlo runs of the GroMiT code, plotted in the final mass–final semimajor axis space. The cross indicates the median mass and semimajor axis of TOI-837 b, while the box shows the associated 3σ range of the planetary mass and semimajor axis. Left: results for both mm-sized (red) and cm-sized (blue) pebbles. Right: same as in the left panel, but including a colour scale to indicate the initial semimajor axes of the planetary seeds.
thumbnail Fig. 11

Illustrative examples of planetary growth tracks falling within the 3σ box for planet b. The growth tracks are projected in the semima-jor axis–planetary mass space. All successful tracks are associated with formation regions comprised between 1 and 4 a and have planetary cores of about 2 M⊕. The core mass is identified by the mass value where the growth tracks intercept the pebble-isolation mass curve (purple line).
thumbnail Fig. 12

Monte Carlo simulations of the interior structures that are compatible within 3σ with the observed planetary radius (dashed green vertical line; the shaded green area include radii within 1σ of the best-fit value) and planetary mass in the solution with 2 GP quasi-periodic kernels, when their uncertainties and the uncertainty on the stellar age are taken into account. Fitting the planetary radius in the case of enhanced opacity of the envelope requires large cores in excess of 30 M⊕, while the faster contraction of envelopes with solar opacity allows for smaller cores compatible with the mass range estimated for Saturn.
thumbnail Fig. 13

Solutions of core–envelope models for planet TOI-837 b with total mass fixed at the measured value, considering both rock-iron core and ice-rock core scenarios with standard and enhanced metallicity. The left panel shows the core mass versus the planetary radius, the middle panel the core radius, and the right panel the atmospheric mass fraction.

5.2 Atmospheric evolution through photo-evaporation

In order to study the atmospheric photo-evaporation over time, we followed a modelling approach initially proposed by Locci et al. (2019), which has been improved in several more recent works, and was most recently described in detail in Mantovan et al. (2024).

Briefly, we evaluated the mass-loss rate of the planetary atmosphere using the analytical approximation derived from the ATES hydrodynamic code (Caldiroli et al. 2021, 2022), coupled with the planetary core–envelope models by Fortney et al. (2007) and Lopez & Fortney (2014), the MESA Stellar Tracks (MIST; Choi et al. 2016), the X-ray luminosity time evolution by Penz et al. (2008), and the X-ray to extreme-ultraviolet (EUV) scaling by Sanz-Forcada et al. (2022).

To perform simulations of the past and future planetary evolution, we explored two core compositions, namely rock-iron (67%, 33%) and ice-rock (25%, 75%); the first is an Earth-like core, the second a Saturn-like core. For computing the planetary radius, we took into account two values of atmospheric metallicity, that is, standard and enhanced metallicity (see Lopez & Fortney 2014). Therefore, we simulated a total of four cases that we named rocki-std and rocki-hi for the standard and enhanced metallicity case, respectively, with an Earth-like core, and icer-std and icer-hi for the standard and enhanced metallicity case, respectively, with a Saturn-like core.

Figure 13 shows the values of the core mass, core radius, and atmospheric mass fraction at the present age as a function of the planetary radius for the various models. With the median values of mass and radius of TOI-837 b in Table 2, the system of equations that describe the planetary structure allows only one solution with a relatively large and massive core. Solutions with a smaller Saturn-like core can be found assuming a larger planetary radius within 1σ of the nominal value for an Earth-like composition, or slightly above 1σ for an ice-rock composition) and/or a smaller planetary mass (at least 3σ below our adopted value). Table 4 reports the values we assume in the following simulations for the mass and radius of the core, for each structure model. These values remain constant in time, while the envelope radius and atmospheric mass fraction may evolve in response to X-ray and UV irradiation.

We determined the XUV flux at the planet, starting with the X-ray luminosity at the present age. Since there is no direct measurement available, we estimated the X-ray luminosity from the Ca II H&K chromospheric index (Sect. 4.2) following Mamajek & Hillenbrand (2008), and we obtained log Lx in the range 3–4 × 1029 erg s−1. On the other hand, their relation with stellar age yields significantly larger values, near ~1 × 1030 erg s−1. We exclude such high values because of the lack of an X-ray detection of this source in the ROSAT All Sky Survey, and ultimately we adopted Lx = 5 × 1029 erg s−1 as derived from the Pizzolato et al. (2003) relation of X-ray luminosity to stellar rotation period.

Figure 14 shows the evolution over time of the atmospheric mass fraction, planetary radius, and mass-loss rate. The values for these parameters at various ages are reported in Table 4. At the present age, we estimate a mass-loss rate of ~5 × 1011 g s−1, which equates to ~2.5 × 10−3 M⊕ Myr−1.

We find that the planet is only slightly affected by hydro-dynamic escape during evolution due to its large mass, which remains mostly unchanged over time in every model we explored. The mass-loss rate, being proportional to the cube of the radius (see Caldiroli et al. 2021, 2022), is higher for models with larger radii, and is of the order of 1012 g s−1 at young ages (3–10 Myr), but these values do not yield significant changes in the atmospheric fraction. Consequently, the evolution of the radius is dominated by the natural gravitational contraction. According to these simulations, the planetary radius was 20–40% larger at an age of 3 Myr, and it will become 20–30% smaller at an age of 1 Gyr. The mass-radius diagram of Fig. 9 shows the expected positions at an age of 1 Gyr for our predicted minimum and maximum values of the radius. If future follow-up observations demonstrate that TOI-837 b has a structure compatible with a rock-iron core and a high opacity atmosphere (see Sect. 5.3), this means that, according to our simulations, the planet will move to a region poorly populated by mature planets, making TOI-837 b an even more interesting object to characterise.

Furthermore, we performed an additional simulation assuming a radius of 10.64 R⊕ (i.e. 1σ from the adopted value) in order to reproduce a Saturn-like core of about 20 M⊕ with a rock-iron composition. Despite the larger radius and consequently higher mass-loss rate compared to previous simulations, we also find in this case that the evolutionary history of the atmosphere is scarcely affected by photo-evaporation due to the high planet’s gravity.

Table 4

Results of the photo-evaporation modelling.

thumbnail Fig. 14

Temporal evolution of mass fraction, radius, and mass-loss rate of TOI-837 b. The left panel shows the evolution of atmospheric mass fraction, the middle panel the evolution of the radius, and the right panel the evolution of the mass-loss rate. Solid lines represent the future evolution, whereas dashed lines show the past evolution.

5.3 Atmospheric characterisation with JWST

Figure 9 (second panel) shows the population of planets younger than 200 Myr and their transmission spectroscopy metric (TSM; Kempton et al. 2018) values. TSM quantifies how much a transiting planet is amenable to atmospheric characterisation through transmission spectroscopy with the JWST. Among all giant planets (Rp > 8 R⊕, Mp > 0.1 MJ) orbiting stars younger than 200 Myr, TOI-837 b has the highest TSM value (∽120), which is greater than the threshold (TSM=90) identified by Kempton et al. (2018) for sub-Jovian planets. In principle, this makes TOI-837 b an ideal candidate for atmospheric characterisation by JWST.

To quantify the prospects for atmospheric characterisation of TOI-837 b with JWST, we employed the open-source PYRAT BAY modelling framework (Cubillos & Blecic 2021) to generate a variety of synthetic transmission and emission spectra. We fed the spectra into the PANDEIA exposure time calculator (Pontoppidan et al. 2016) to simulate transit and eclipse signals as observed by the JWST instruments and their S/N.

The PYRAT BAY package enables self-consistent atmospheric modelling (pressure, temperature, and composition) under an iterative radiative and thermochemical equilibrium calculation for a set of assumed physical conditions (Cubillos et al., in prep.). The equilibrium temperature of ∽1000 K makes TOI-837 b a particularly valuable target for atmospheric characterisation, because slight changes in the temperature or metallicity can lead to widely different compositions, each with clear and distinct observable outcomes. Therefore, to emphasise the extent to which the observable properties of TOI-837 b can change, we explored scenarios spanning the range of expected atmospheric metallicities and irradiation/dynamics conditions. The right panels of Fig. 15 show the temperature and composition profiles for two selected scenarios. The first scenario has a solar metallicity, zero Bond albedo, and an efficient day–night energy redistribution (i.e. a heat-redistribution factor of f = 1/4; see e.g. Spiegel & Burrows 2010). The second scenario has an atmospheric metallicity of 50× solar, zero Bond albedo, and poor day–night energy redistribution (f = 2/3). As expected, the model with higher energy redistribution (1× solar model) has a cooler temperature profile (a difference of a few hundred K). The main consequence of this lower temperature is the proportionally larger CH4 abundance for the 1 × solar model compared to the 50× solar model. On the other hand, the main consequence of a higher metallicity is the proportionally larger CO2 abundance. Both of these factors have a direct impact on the observable properties of the planet for either transit or eclipse observations.

For the JWST simulations, we initially considered all possible spectroscopic modes available: given the host star’s spectral type and magnitude, all instruments can observe the system without reaching saturation. We find the NIRISS/SOSS, NIRSpec/G395H, and MIRI/LRS settings to be the optimal configurations, as they provide the best S/N and the broadest spectral coverage. The left panels of Fig. 15 show the simulated transmission and emission observations for our two scenarios, considering a single transit and occultation and a single realisation per instrument, accounting for random noise added to the data. In transmission, all three instruments can provide valuable abundance constraints: in particular, H2O has a series of bands at the shorter wavelength end of the spectrum, being probed by NIRISS/SOSS; CO2 has its strongest absorption band at 4.4 µm, being probed by NIRSpec/G395H; and CH4 has multiple bands that are readily detectable by all three instruments. In emission, the lower planetary flux at the shorter wavelengths makes NIRISS/SOSS the most challenging observation; however, both NIRSpec/G395H and MIRI/LRS can provide clear detection of atmospheric species, such as CO2 and CH4.

Given the S/N of these simulations, JWST can not only detect the presence (or absence) of multiple molecular features on TOI-837 b, but it can also constrain the abundance of specific species (along with the atmospheric thermal structure) by measuring the amplitude of their absorption bands. Finding muted spectral features would instead indicate the presence of clouds and hazes. Lastly, these observations also have the potential to probe the presence of refractory elements, which would constrain the formation and evolution of the system. For example, NIRISS/SOSS transmission observations can probe the signature of K at 0.77 µm (not shown in Fig. 15). NIRSpec and MIRI can probe the signature of SO2 at 4.0 and 7.5 µm, respectively, which could become observable at sufficiently high abundances. In fact, in this way these observations could also become a probe for disequilibrium-chemistry processes, as processes like vertical transport and photochemistry are indeed pathways to enhancement of the abundance of certain species, including SO2 (Tsai et al. 2023).

thumbnail Fig. 15

JWST observation simulations of TOI-837 b. Left panels: transit (top) and eclipse (bottom) simulations of JWST spectra for two scenarios: a solar-metallicity atmosphere with efficient day–night energy redistribution (red) and a 50× solar-metallicity atmosphere with poor energy redistribution (blue). The markers with error bars show one realisation of an observation with the expected uncertainties (assuming a single observation per instrument). The coloured labels at the top denote the instrument and spectral range of the simulated observations. The solid curves denote the underlying ‘true’ astrophysical models. The main molecular bands discussed in the text are indicated. Top-right panel: radiative-thermochemical-equilibrium temperature profiles, which are the basis for the simulations and atmospheric modelling. Bottom-right panel: atmospheric abundances for the 1 × (solid curves) and 50× solar metallicity model (dashed curves) for selected species (see legend).

6 Summary and prospects

In this work, we analysed and characterised the infant planetary system TOI-837 detected by TESS in the open cluster IC 2602, measuring the fundamental properties of the host star and of the close-in planet TOI-837 b through the modelling of photometric (TESS) and spectroscopic (HARPS) datasets. We find that TOI-837 b has a mass, radius, and bulk density that are similar to those of Saturn (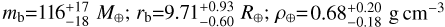mb=116−18+17M⊕;rb=9.71−0.60+0.93R⊕;ρ⊕=0.68−0.18+0.20 g cm−3${m_{\rm{b}}} = 116_{ - 18}^{ + 17}{M_ \oplus };{r_{\rm{b}}} = 9.71_{ - 0.60}^{ + 0.93}{R_ \oplus };{\rho _ \oplus } = 0.68_{ - 0.18}^{ + 0.20}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$). We did not find evidence for additional planetary companions in the system. Nonetheless, we identified a low-mass star that is likely gravitationally bound to TOI-837, and orbits at a separation of ~330 au. The discovery of an infant Saturn-mass planet (stellar age ~35 Myr) that closely orbits its parent star (ab ~ 0 .08 au) highlights fundamental questions regarding the formation and evolutionary histories of this planetary system. In the present study, we first investigated the possible formation scenarios and predicted internal structure of TOI-837 b that show compatibility with the measured mass and radius. We then reconstructed the evolution of the planet’s atmosphere driven by photo-evaporation. In the following, we summarise our findings:

  • Our formation and early migration models suggest two solutions for TOI-837 b, one with a relatively large and massive core, and the other with a smaller Saturn-like core, depending on the opacity of the protoplanetary gas and on the growth rate of the core;

  • For the cases of standard opacity, we obtain synthetic planets with radius, mass, and density within 1σ of the best-fit (median) values in ~30% of the possible interior structures, and 5–6% of the total synthetic planets have core masses of below 25 M⊕;

  • At its current age, because of the uncertainties on the planetary parameters and stellar age, the planet could have a structure with a massive core (40–80 M⊕, depending on the actual core composition and opacity of the envelope), and a thick and heavy atmosphere (6–7 R⊕, and 30–60% the total mass), with a relatively low mass-loss rate (2 . 5 × 10−3 M⊕ Myr−1). The possible solutions with a Saturn-like core and larger atmospheric mass fractions require a larger planetary radius (within 1σ of our nominal value in the case of a core with Earth-like composition), or a smaller mass;

  • In either of the possible cases, our simulations of the evolutionary history indicate that the planet was little affected by photo-evaporation, even at early ages (3–10 Myr), because of the relatively weak XUV irradiation and deep gravitational potential well. We conclude that the position of TOI-837 b on the mass-radius diagram is expected to change slightly throughout its lifetime; that is, unless follow-up observations reveal that the structure of the planet is compatible with a rocky-iron core and a high-opacity atmosphere, in which case, we predict that TOI-837 b would move to a region of the diagram poorly populated by mature planets.

Based on our results, interesting questions arise that make TOI-837 a primary target for follow-up observations. We advocate in particular for a more accurate and precise radius determination of TOI-837 b through high-precision and high-angular-resolution photometry, which would allow a choice between the possible internal structures predicted by our population synthesis model. The same scientific case strongly motivates a follow-up of TOI-837 with JWST. As we demonstrate, TOI-837b is a perfect target for transmission and emission spectroscopy with JWST, which will help to constrain the composition and molecular abundances of the atmospheric envelope and, consequently, the actual internal structure of the planet.

Being a short-period giant planet, TOI-837 b is a suitable target for measurement of its 3D obliquity with respect to the stellar rotation axis by detecting the Rossiter-McLaughlin (RM) effect (Rossiter 1924; McLaughlin 1924; Ohta et al. 2005). With an expected amplitude of the RM signature of >10 m s−1, the target is amenable to follow-up analyses with high-resolution spectro-graphs, such as ESPRESSO, which allowed for the detection of the RM effect in the case of DS Tuc A b (Benatti et al. 2021). So far, the RM effect has only been detected for a handful of stars with ages of <100 Myr, and each of the obliquity measurements is consistent with zero (e.g. Heitzmann et al. 2021; Albrecht et al. 2022). It is important to verify this trend by measuring the obliquity of TOI-837b, which could also be used to endorse or refute the scenario that the close-in planet underwent disc migration, as suggested by its orbital architecture. Alternatively, the gravitational pull exerted by the bound stellar companion to TOI-837 (discussed in Sect. 3.2) might have excited a high orbital obliquity of planet b.

Acknowledgements

We acknowledge the anonymous referee for insightful comments. DPo acknowledges the support from the Istituto Nazionale di Oceanografia e Geofisica Sperimentale (OGS) and CINECA through the program “HPC-TRES (High Performance Computing Training and Research for Earth Sciences)” award number 2022-05 as well as the support of the ASI-INAF agreement no. 2021-5-HH.1-2022. A.Ma. acknowledges partial support from the PRIN-INAF 2019 (project HOT-ATMOS), and the ASI-INAF agreement n 2021.5-HH.1-2022. P.Cu. is funded by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, program J4595-N. G.Ma. acknowledges support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. This work has been supported by the PRIN-INAF 2019 “Planetary systems at young ages (PLATEA)”.

Appendix A Data and additional plots

thumbnail Fig. A.1

Corner plot showing the posterior distributions of the free (hyper-)parameters for our adopted joint RV+light curve model discussed in Sect. 4.3 (two GP quasi-periodic signals plus two sinusoids). Instead of a single corner plot, two subplots (a) and (b) are shown for a better readability, preserving the visibility of correlations for a few parameters.
thumbnail Fig. A.2

Pre-whitened CRX activity index plotted versus the RVs of the long-period sinusoid included in our adopeted best-fit RV model. The correlation coefficient is ρPearson=+0.71, indicating that the RV signal is very likely due to stellar activity.
Table A.1

HARPS radial velocities.

Table A.2

Time series of the activity diagnostics considered in this work.

References

  1. Albrecht, S. H., Dawson, R. I., & Winn, J. N. 2022, PASP, 134, 082001 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alsubai, K., Mislis, D., Tsvetanov, Z. I., et al. 2017, AJ, 153, 200 [Google Scholar]
  3. Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Transactions on Pattern Analysis and Machine Intelligence, 38, 2 [Google Scholar]
  4. Atreya, S. K., Crida, A., Guillot, T., et al. 2018, in Saturn in the 21st Century, eds. K. H. Baines, F. M. Flasar, N. Krupp, & T. Stallard, 5 [CrossRef] [Google Scholar]
  5. Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barragán, O., Yu, H., Freckelton, A. V., et al. 2024, MNRAS, 531, 4275 [CrossRef] [Google Scholar]
  7. Battley, M. P., Armstrong, D. J., & Pollacco, D. 2022, MNRAS, 511, 4285 [NASA ADS] [CrossRef] [Google Scholar]
  8. Benatti, S., Nardiello, D., Malavolta, L., et al. 2019, A&A, 630, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Benatti, S., Damasso, M., Borsa, F., et al. 2021, A&A, 650, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Berger, T. A., Huber, D., Gaidos, E., van Saders, J. L., & Weiss, L. M. 2020, AJ, 160, 108 [NASA ADS] [CrossRef] [Google Scholar]
  11. Biazzo, K., Randich, S., & Palla, F. 2011, A&A, 525, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
  14. Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bonomo, A. S., Desidera, S., Benatti, S., et al. 2017, A&A, 602, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Booth, R. A., & Ilee, J. D. 2019, MNRAS, 487, 3998 [CrossRef] [Google Scholar]
  17. Bouma, L. G., Hartman, J. D., Brahm, R., et al. 2020, AJ, 160, 239 [Google Scholar]
  18. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  19. Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Caldiroli, A., Haardt, F., Gallo, E., et al. 2021, A&A, 655, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Caldiroli, A., Haardt, F., Gallo, E., et al. 2022, A&A, 663, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Canocchi, G., Malavolta, L., Pagano, I., et al. 2023, A&A, 672, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, 210, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, A20 [NASA ADS] [Google Scholar]
  24. Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
  25. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  26. Crossfield, I. J. M. 2023, ApJ, 952, L18 [NASA ADS] [CrossRef] [Google Scholar]
  27. Cubillos, P. E., & Blecic, J. 2021, MNRAS, 505, 2675 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
  29. Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR Online Data Catalog II/328 [Google Scholar]
  30. Damasso, M., Lanza, A. F., Benatti, S., et al. 2020, A&A, 642, A133 [EDP Sciences] [Google Scholar]
  31. David, T. J., Hillenbrand, L. A., Petigura, E. A., et al. 2016, Nature, 534, 658 [CrossRef] [Google Scholar]
  32. David, T. J., Petigura, E. A., Luger, R., et al. 2019, ApJ, 885, L12 [Google Scholar]
  33. Eastman, J. 2017, EXOFASTv2: Generalized publication-quality exoplanet modeling code, Astrophysics Source Code Library [record ascl:1710.003] [Google Scholar]
  34. Eastman, J. D., Rodriguez, J. E., Agol, E., et al. 2019, arXiv e-prints [arXiv: 1907.09480] [Google Scholar]
  35. Feinstein, A. D., David, T. J., Montet, B. T., et al. 2022, ApJ, 925, L2 [NASA ADS] [CrossRef] [Google Scholar]
  36. Feroz, F., Hobson, M. P., Cameron, E., & Pettitt, A. N. 2019, Open J. Astrophys., 2, 10 [Google Scholar]
  37. Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [Google Scholar]
  38. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
  42. Gomes da Silva, J., Figueira, P., Santos, N., & Faria, J. 2018, J. Open Source Softw., 3, 667 [Google Scholar]
  43. Gomes da Silva, J., Santos, N. C., Adibekyan, V., et al. 2021, A&A, 646, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gupta, A., & Schlichting, H. E. 2019, MNRAS, 487, 24 [Google Scholar]
  45. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
  47. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  48. Heitzmann, A., Zhou, G., Quinn, S. N., et al. 2021, ApJ, 922, L1 [NASA ADS] [CrossRef] [Google Scholar]
  49. Henden, A. A., Levine, S., Terrell, D., & Welch, D. L. 2015, AAS Meeting Abstracts, 225, 336.16 [Google Scholar]
  50. Hidalgo, S. L., Pietrinferni, A., Cassisi, S., et al. 2018, ApJ, 856, 125 [Google Scholar]
  51. Hippke, M., David, T. J., Mulders, G. D., & Heller, R. 2019, AJ, 158, 143 [Google Scholar]
  52. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
  53. Jeffries, R. D., Jackson, R. J., Wright, N. J., et al. 2023, MNRAS, 523, 802 [NASA ADS] [CrossRef] [Google Scholar]
  54. Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Kempton, E. M. R., Bean, J. L., Louie, D. R., et al. 2018, PASP, 130, 114401 [Google Scholar]
  56. Kipping, D. M. 2010, MNRAS, 408, 1758 [Google Scholar]
  57. Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
  58. Lin, D. N. C., & Ida, S. 2004, Star Formation in the Interstellar Medium: In Honor of David Hollenbach, eds. D. Johnstone, F. C. Adams, D. N. C. Lin, D. A. Neufeeld, & E. C. Ostriker, ASP Conf. Ser., 323, 339 [NASA ADS] [Google Scholar]
  59. Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Linder, E. F., Mordasini, C., Mollière, P., et al. 2019, A&A, 623, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Locci, D., Cecchi-Pestellini, C., & Micela, G. 2019, A&A, 624, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [Google Scholar]
  63. Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
  64. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [Google Scholar]
  65. Mankovich, C. R., & Fuller, J. 2021, Nat. Astron., 5, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  66. Mann, A. W., Newton, E. R., Rizzuto, A. C., et al. 2016, AJ, 152, 61 [Google Scholar]
  67. Mann, A. W., Wood, M. L., Schmidt, S. P., et al. 2022, AJ, 163, 156 [NASA ADS] [CrossRef] [Google Scholar]
  68. Mantovan, G., Montalto, M., Piotto, G., et al. 2022, MNRAS, 516, 4432 [NASA ADS] [CrossRef] [Google Scholar]
  69. Mantovan, G., Malavolta, L., Locci, D., et al. 2024, A&A, 684, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Markwardt, C. B. 2009, Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
  71. Martioli, E., Hébrard, G., Correia, A. C. M., Laskar, J., & Lecavelier des Etangs, A. 2021, A&A, 649, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Matsumura, S., Takeda, G., & Rasio, F. A. 2008, ApJ, 686, L29 [Google Scholar]
  73. McLaughlin, D. B. 1924, ApJ, 60, 22 [Google Scholar]
  74. Middelkoop, F. 1982, A&A, 113, 1 [NASA ADS] [Google Scholar]
  75. Nagasawa, M., & Ida, S. 2011, ApJ, 742, 72 [NASA ADS] [CrossRef] [Google Scholar]
  76. Nardiello, D. 2020, MNRAS, 498, 5972 [Google Scholar]
  77. Nardiello, D., Borsato, L., Piotto, G., et al. 2019, MNRAS, 490, 3806 [NASA ADS] [CrossRef] [Google Scholar]
  78. Nardiello, D., Piotto, G., Deleuil, M., et al. 2020, MNRAS, 495, 4924 [Google Scholar]
  79. Nardiello, D., Deleuil, M., Mantovan, G., et al. 2021, MNRAS, 505, 3767 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nardiello, D., Malavolta, L., Desidera, S., et al. 2022, A&A, 664, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Newton, E. R., Mann, A. W., Tofflemire, B. M., et al. 2019, ApJ, 880, L17 [Google Scholar]
  82. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  83. Ohta, Y., Taruya, A., & Suto, Y. 2005, ApJ, 622, 1118 [Google Scholar]
  84. Owen, J. E. 2020, MNRAS, 498, 5030 [Google Scholar]
  85. Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
  86. Pacetti, E., Turrini, D., Schisano, E., et al. 2022, ApJ, 937, 36 [NASA ADS] [CrossRef] [Google Scholar]
  87. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  88. Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
  90. Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Plavchan, P., Barclay, T., Gagné, J., et al. 2020, Nature, 582, 497 [Google Scholar]
  92. Pontoppidan, K. M., Pickering, T. E., Laidler, V. G., et al. 2016, SPIE Conf. Ser., 9910, 991016 [NASA ADS] [Google Scholar]
  93. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
  94. Rizzuto, A. C., Newton, E. R., Mann, A. W., et al. 2020, AJ, 160, 33 [Google Scholar]
  95. Rossiter, R. A. 1924, ApJ, 60, 15 [Google Scholar]
  96. Sanz-Forcada, J., López-Puertas, M., Nortmann, L., & Lampón, M. 2022, 21st Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, https://backoffice.inviteo.com/upload/compte153/Base/inscriptions_projets/fichier/108345-posterjsanzcs21.pdf [Google Scholar]
  97. Schneider, A. D., & Bitsch, B. 2021, A&A, 654, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Shibata, S., Helled, R., & Ikoma, M. 2020, A&A, 633, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
  101. Sneden, C. 1973, ApJ, 184, 839 [Google Scholar]
  102. Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [Google Scholar]
  103. Spiegel, D. S., & Burrows, A. 2010, ApJ, 722, 871 [NASA ADS] [CrossRef] [Google Scholar]
  104. Stevenson, D. J. 2020, Annu. Rev. Earth Planet. Sci., 48, 465 [CrossRef] [Google Scholar]
  105. Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
  106. Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
  107. Suárez Mascareño, A., Damasso, M., Lodieu, N., et al. 2021, Nat. Astron., 6, 232 [Google Scholar]
  108. Tanaka, H., Murase, K., & Tanigawa, T. 2020, ApJ, 891, 143 [NASA ADS] [CrossRef] [Google Scholar]
  109. Tsai, S.-M., Lee, E. K. H., Powell, D., et al. 2023, Nature, 617, 483 [CrossRef] [Google Scholar]
  110. Türrini, D., Schisano, E., Fonte, S., et al. 2021, ApJ, 909, 40 [NASA ADS] [CrossRef] [Google Scholar]
  111. Turrini, D., Marzari, F., Polychroni, D., et al. 2023, A&A, 679, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
  114. Zakhozhay, O. V., Launhardt, R., Trifonov, T., et al. 2022, A&A, 667, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
  116. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Zicher, N., Barragán, O., Klein, B., et al. 2022, MNRAS, 512, 3060 [NASA ADS] [CrossRef] [Google Scholar]
1

We refer to these as ‘infant’ planets throughout the paper.

2

The code is publicly available at https://github.com/mzechmeister/serval. We used the command line -safemode 2 -niter 4 -snmίn 25 -ofαc 0.30 -vrαnge 30 to process the HARPS spectra with SERVAL. We adopted a decreased oversampling factor for the spectra co-adding (i.e. ofac=0.3) as suggested by Zechmeister et al. (2018) to obtain a smoother template in case of noisy observations or fast rotators.

5

The four confirmed planets of the 20 Myr old system V1298 Tau are not shown in the mass-radius diagram. The high complexity encountered so far in modeling and characterising this system resulted in quite different published values for the planets’ masses, with no consensus reached yet.

All Tables

Table 1

Stellar parameters of TOI-837 (CPD-63 1435).

In the text
Table 2

Priors and best-fit values of the free and derived parameters related to the joint RV+light curve modelling.

In the text
Table 3

Input parameters used to run the MC modified GroMiT code to produce simulated planets and investigate the formation history of TOI-837b.

In the text
Table 4

Results of the photo-evaporation modelling.

In the text
Table A.1

HARPS radial velocities.

In the text
Table A.2

Time series of the activity diagnostics considered in this work.

In the text

All Figures

thumbnail Fig. 1

Gαiα DR3 stars identified in the TESS field of view of TOI-837, which is identified by the letter ‘t’. Several stellar contaminants fall within the TESS aperture. Δm denotes the magnitude difference in the Gaia G-band between each field star and TOI-837.
In the text
thumbnail Fig. 2

Short-cadence lightcurves of TOI-837 observed by TESS in Sectors 10 and 11 (top panel), 37 and 38 (middle panel), and 63 and 64 (bottom panel). For each pair of sectors, we report the short-cadence light curve and the detrending model (in azure), and the corresponding flattened light curve. The transits of TOI-837 b are indicated with red triangles.
In the text
thumbnail Fig. 3

Spectral energy distribution of TOI-837 with the best-fit model over-plotted (solid line). Red and blue points correspond to the observed and predicted values, respectively.
In the text
thumbnail Fig. 4

Proper motions and colour-magnitude diagram of the members of the open cluster IC 2602. Top panel shows the proper motions of the cluster members (in black) after a selection based on the parallax and the proper motions themselves. Bottom panel shows the Gaia G-mag versus BP-RP colour–magnitude diagram of the same stars with a BASTI-IAC isochrone of 35 Myr superimposed. In both panels, green symbols represent the target of this study.
In the text
thumbnail Fig. 5

Time series and periodogram of the HARPS RVs. Upper panel: RV time series of TOI-837 (SERVAL extraction). Middle panel: GLS periodogram of the original and prewhitened data. False-alarm probability levels for the periodogram of the original RV dataset are indicated by horizontal dashed lines. Lower panel: window function of the data.
In the text
thumbnail Fig. 6

Time series and periodogram of spectroscopic activity diagnostics calculated from HARPS spectra. Left pαnel: time series (black dots) of activity diagnostics extracted from HARPS spectra. Right panel: GLS periodograms of the time series, and prewhitened time series, shown in the left panel. The vertical green line identifies the stellar rotation period measured from the TESS light curve.
In the text
thumbnail Fig. 7

Best-fit models related to the RV dataset obtained from the joint RV+light curve analysis described in Sect. 4.3. First row: RV time series with the adopted best-fit model over-plotted (red curve; activity plus Doppler signal due to TOI-837 b). Second row: phase-folded Doppler RV signal of TOI-837 due to planet b (left panel), and the signal with a period of ∽ 74 days, which we interpret as due to stellar activity (right panel). Nominal error bars are indicated in black, while the error bars with an uncorrelated jitter term added in quadrature are indicated in green. Third row: stellar-activity-correlated signal in the RV time series (red dots) as fitted by a GP regression including the sum of two quasi-periodic kernels. The blue line represents the best-fit model, and the 1σ confidence interval is shown as a shaded grey area. The panel on the right is a zoomed-in view of the left panel, for better readability. To calculate all the theoretical curves shown here, we adopted the median values of the model parameters in Table 2.
In the text
thumbnail Fig. 8

Phase-folded transit light curve of TOI-837 b, and O–C residuals. The data point on the bottom right of the first panel shows the median error bar of the complete photometric time series.
In the text
thumbnail Fig. 9

Mass–radius diagram for a comparison between planets younger than 200 Myr and a mature population, and for assessing the prospects for a follow-up of TOI-837 b with JWST. Upper panel: mass-radius diagrams showing transiting planets with ages of less than 200 Myr (black symbols), taking the upper uncertainties on age into account for the definition of the age bin. Black dots indicate planets with a measured mass, while black triangles represent planets for which only an upper limit on mass is available. Grey dots represent a sample of older planets for which masses and radii have been measured with a precision of at least 30% and 10%, respectively. The current location of the planet TOI-837 b is indicated with a red dot, while the red asterisk and cross symbols denote the expected locations at an age of 1 Gyr for the cases of rock-ice core+low atmospheric opacity and rock-iron core+high atmospheric opacity, respectively (see Table 4 and Sect. 5.2 for details). A red triangle indicates the location of the planet DS Tuc Ab (1σ mass upper limit; Benatti et al. 2021). Saturn is identified by a blue dot. Diagonal dashed lines indicate the locations of planets with an equal density. Lower panel: mass–radius diagram of planets younger than 200 Myr, with dot size representing the TSM metrics for prospects of spectro-scopic follow-up with JWST. The mass of the planets is shown on a logarithmic scale. The giant planets (Rp > 8 R⊕ and Mp > 0.1 MJ) are represented within the light green area.
In the text
thumbnail Fig. 10

Synthetic planetary populations resulting from the Monte Carlo runs of the GroMiT code, plotted in the final mass–final semimajor axis space. The cross indicates the median mass and semimajor axis of TOI-837 b, while the box shows the associated 3σ range of the planetary mass and semimajor axis. Left: results for both mm-sized (red) and cm-sized (blue) pebbles. Right: same as in the left panel, but including a colour scale to indicate the initial semimajor axes of the planetary seeds.
In the text
thumbnail Fig. 11

Illustrative examples of planetary growth tracks falling within the 3σ box for planet b. The growth tracks are projected in the semima-jor axis–planetary mass space. All successful tracks are associated with formation regions comprised between 1 and 4 a and have planetary cores of about 2 M⊕. The core mass is identified by the mass value where the growth tracks intercept the pebble-isolation mass curve (purple line).
In the text
thumbnail Fig. 12

Monte Carlo simulations of the interior structures that are compatible within 3σ with the observed planetary radius (dashed green vertical line; the shaded green area include radii within 1σ of the best-fit value) and planetary mass in the solution with 2 GP quasi-periodic kernels, when their uncertainties and the uncertainty on the stellar age are taken into account. Fitting the planetary radius in the case of enhanced opacity of the envelope requires large cores in excess of 30 M⊕, while the faster contraction of envelopes with solar opacity allows for smaller cores compatible with the mass range estimated for Saturn.
In the text
thumbnail Fig. 13

Solutions of core–envelope models for planet TOI-837 b with total mass fixed at the measured value, considering both rock-iron core and ice-rock core scenarios with standard and enhanced metallicity. The left panel shows the core mass versus the planetary radius, the middle panel the core radius, and the right panel the atmospheric mass fraction.
In the text
thumbnail Fig. 14

Temporal evolution of mass fraction, radius, and mass-loss rate of TOI-837 b. The left panel shows the evolution of atmospheric mass fraction, the middle panel the evolution of the radius, and the right panel the evolution of the mass-loss rate. Solid lines represent the future evolution, whereas dashed lines show the past evolution.
In the text
thumbnail Fig. 15

JWST observation simulations of TOI-837 b. Left panels: transit (top) and eclipse (bottom) simulations of JWST spectra for two scenarios: a solar-metallicity atmosphere with efficient day–night energy redistribution (red) and a 50× solar-metallicity atmosphere with poor energy redistribution (blue). The markers with error bars show one realisation of an observation with the expected uncertainties (assuming a single observation per instrument). The coloured labels at the top denote the instrument and spectral range of the simulated observations. The solid curves denote the underlying ‘true’ astrophysical models. The main molecular bands discussed in the text are indicated. Top-right panel: radiative-thermochemical-equilibrium temperature profiles, which are the basis for the simulations and atmospheric modelling. Bottom-right panel: atmospheric abundances for the 1 × (solid curves) and 50× solar metallicity model (dashed curves) for selected species (see legend).
In the text
thumbnail Fig. A.1

Corner plot showing the posterior distributions of the free (hyper-)parameters for our adopted joint RV+light curve model discussed in Sect. 4.3 (two GP quasi-periodic signals plus two sinusoids). Instead of a single corner plot, two subplots (a) and (b) are shown for a better readability, preserving the visibility of correlations for a few parameters.
In the text
thumbnail Fig. A.2

Pre-whitened CRX activity index plotted versus the RVs of the long-period sinusoid included in our adopeted best-fit RV model. The correlation coefficient is ρPearson=+0.71, indicating that the RV signal is very likely due to stellar activity.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

OSZAR »