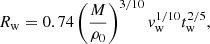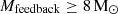| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202348840 | |
| Published online | 02 October 2024 | |
Massive star cluster formation
I. High star formation efficiency while resolving feedback of individual stars
1
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik, Heidelberg, Germany
2
Department of Astrophysics, American Museum of Natural History, New York, NY, USA
3
Department of Physics, Drexel University, Philadelphia, PA, USA
4
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, Heidelberg, Germany
5
Department of Physics and Astronomy, McMaster University, Hamilton, ON, Canada
6
Department of Physics and Astronomy, Rutgers University, Piscataway, NJ, USA
7
Department of Physics, University of Wisconsin–Madison, Madison, WI, USA
8
Sterrewacht Leiden, Leiden University, Leiden, The Netherlands
9
Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
10
School of Physics and Astronomy, Sun Yat-sen University, Daxue Road, Zhuhai 519082, China
Received:
5
December
2023
Accepted:
5
June
2024
The mode of star formation that results in the formation of globular clusters and young massive clusters is difficult to constrain through observations. We present models of massive star cluster formation using the TORCH framework, which uses the Astrophysical MUltipurpose Software Environment (AMUSE) to couple distinct multi-physics codes that handle star formation, stellar evolution and dynamics, radiative transfer, and magnetohydrodynamics. We upgraded TORCH by implementing the N-body code PETAR, thereby enabling TORCH to handle massive clusters forming from 106 M⊙ clouds with ≥105 individual stars. We present results from TORCH simulations of star clusters forming from 104, 105, and 106 M⊙ turbulent spherical gas clouds (named M4, M5, M6) of radius R = 11.7 pc. We find that star formation is highly efficient and becomes more so at a higher cloud mass and surface density. For M4, M5, and M6 with initial surface densities 2.325 × 101,2,3 M⊙ pc−2, after a free-fall time of tff = 6.7,2.1,0.67 Myr, we find that ∼30%, 40%, and 60% of the cloud mass has formed into stars, respectively. The end of simulation-integrated star formation efficiencies for M4, M5, and M6 are ϵ⋆ = M⋆/Mcloud = 36%, 65%, and 85%. Observations of nearby clusters similar in mass and size to M4 have instantaneous star formation efficiencies of ϵinst ≤ 30%, which is slightly lower than the integrated star formation efficiency of M4. The M5 and M6 models represent a different regime of cluster formation that is more appropriate for the conditions in starburst galaxies and gas-rich galaxies at high redshift, and that leads to a significantly higher efficiency of star formation. We argue that young massive clusters build up through short efficient bursts of star formation in regions that are sufficiently dense (Σ ≥ 102 M⊙ pc−2) and massive (Mcloud ≥ 105 M⊙). In such environments, stellar feedback from winds and radiation is not strong enough to counteract the gravity from gas and stars until a majority of the gas has formed into stars.
Key words: ISM: clouds / galaxies: star clusters: general / galaxies: star formation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Globular clusters (GCs), which are found in every massive galaxy, are some of the most ancient objects in the Universe. They serve as fossils that can reveal the elusive environment and physics of the early phases of galaxy assembly (Brodie & Strader 2006; Portegies Zwart et al. 2010; Renaud et al. 2017; Krumholz et al. 2019; Adamo et al. 2020). Yet because of their age, many aspects of cluster formation and evolution at high redshift are challenging to constrain through observation, and little is known about the efficiency and timescale at which gas is converted into stars to create such massive bound clusters.
Though the progenitors of GCs are too old to observe, there are younger star clusters that are as massive as GCs and currently forming in nearby galaxies. These young massive clusters (YMCs) have masses M ≥ 104 M⊙ and ages < 100 Myr (Portegies Zwart et al. 2010). The discovery of these objects has indicated that the mode of extreme star formation that forms massive star clusters still occurs today. Notably, even more of these clusters are being discovered with JWST, as many YMCs in starburst galaxies are too embedded to have been seen by Hubble (Whitmore et al. 2023). Although it has been suggested that YMCs are the present day analogs to young GCs, this is debated in the literature (see Renaud 2020).
Theory suggests that, despite the abundance of GCs, ≤1% of clusters survive to become GCs (Fall & Zhang 2001; Fall et al. 2005; Fall 2006). The conditions that lead to bound star clusters as massive as GCs remain a mystery, and observations of forming YMCs are sparse. Star formation must be fast and efficient enough to form bound stars that can survive the epoch of stellar feedback and the dispersal of the natal gas (Lada & Lada 2003). The plethora of GCs suggests these conditions were very common in the early Universe.
The process of star formation in a cluster begins with the global gravo-turbulent collapse of giant molecular clouds (GMCs; Larson 1981). As the collapse proceeds, fragmentation creates overdense clumps within the GMC that begin to form stars (Mac Low & Klessen 2004; McKee & Ostriker 2007; Klessen & Glover 2016). The feedback from these stars, in the form of stellar winds, jets, and radiation, begins to clear out dense gas in and around the forming sub-clusters, slowing down the local (sub-cluster scale) and global (cloud scale) star formation rate (SFR; e.g., Girichidis et al. 2020; Lewis et al. 2023). Eventually, massive stars explode as supernovae (SNe), further dispersing gas. However, it has been argued that the efficiency at which stellar feedback slows global star formation diminishes with higher gas surface density (Grudić et al. 2018). The sub-clusters eventually merge if they are mutually gravitationally bound, forming a final cluster cleared of all natal gas (Krause et al. 2020).
Many details of star cluster formation remain poorly understood due to the difficulty of modelling such a complex process. Stellar evolution and binary dynamics need to be resolved on timescales of years and distance scales of an AU, while the magnetohydrodynamics (MHD) of the collapsing gas covers regions several parsecs across, with crossing times of thousands to millions of years. Because of this, most computational star cluster formation models are limited and must make considerable approximations. Many simulations do not form individual stars: some apply stellar feedback as a combined source in the center of the cloud (Dale et al. 2005; Rahner et al. 2019), and others use sink particles representing sub-clusters (e.g., Bate et al. 1995; Federrath et al. 2010) or extract the properties and feedback of individual stars from the sink particles (e.g., Sormani et al. 2017; Howard et al. 2017; Kim et al. 2017; Grudić et al. 2018; Su et al. 2018). Other simulations do form single stars, but they do not resolve the stellar feedback of each individual star particle (Colín et al. 2013a; Li et al. 2019), instead including feedback from just the sink particles that created the stars. Simulations of dwarf galaxies can capture star cluster mass functions and formation times, but they do so without collisional dynamics of star particles and are therefore unable to accurately capture dynamical properties such as velocity dispersion and size (Lahén et al. 2019, 2024; Andersson et al. 2024).
Modelling individual stars is important, as this can change the efficiency and location of stellar feedback injection. Dynamical processes often eject high-mass stars (Fujii & Portegies Zwart 2011; Fujii et al. 2022a), and the location of massive stars directly affects how and when gas is dispersed. Gas dispersal stops star formation. Models of sub-cluster feedback may overestimate the strength of feedback, as they do not allow for spatial separation between the stars in the sub-cluster. This lack of separation also changes the morphology of the gas, affecting the number of low-density channels in the gas that can vent thermal energy from the sub-cluster. The degree to which the sub-cluster and star-by-star approaches differ must be constrained.
There are a few models that do evolve individual stars with both stellar feedback and higher order gravitational dynamics (Wall et al. 2020; Grudić et al. 2021; Fujii et al. 2021, 2022b,a; Cournoyer-Cloutier et al. 2021, 2023; Lewis et al. 2023; Wilhelm et al. 2023). While these models include most of the relevant physics, they lack the computational efficiency to simulate star clusters forming from clouds of masses > 105 M⊙, and instead the models focus on simulating star clusters forming from low-mass clouds ≤105 M⊙. This leaves a sizeable gap compared to the observed mass range of GMCs. While clusters with mass < 105 M⊙ are comparable to Local Group observations, YMC and GC formation is out of their reach. Furthermore, most star formation takes place in GMCs of mass ≥105 M⊙ (McKee & Williams 1997; Murray & Rahman 2009).
The goal of this work is to model the formation of massive clusters from their initial GMCs while following the formation of individual stars and their feedback. We aim to answer how and in what conditions YMCs can form while remaining bound throughout the onset of gas expulsion. We also seek to understand how efficient the process of star formation is in a cluster, what the timescale is over which star formation occurs, and whether the clusters formed from these massive clouds survive and remain bound or quickly disperse. We plan to compare our results to those that use a sub-cluster formation and feedback model.
To do this, we used the TORCH framework (Wall et al. 2019, 2020). TORCH employs the Astrophysical Multipurpose Software Environment (AMUSE) framework to couple separate physics codes that handle MHD, radiative transfer, stellar evolution, and N-body dynamics. TORCH uses the MHD code FLASH (Fryxell et al. 2000; Dubey et al. 2014), which accounts for the evolution of the gas and the formation of sink particles and stars. Stellar feedback in the form of winds and SNe is included, and the effect of ionizing and non-ionizing radiation is followed using a ray-tracing approach (Baczynski et al. 2015). The star formation model samples the Kroupa (2002) initial mass function (IMF) to form stars from sink mass reservoirs (Wall et al. 2019). SEBA (Portegies Zwart & Verbunt 1996) tracks stellar evolution from the zero-age main sequence, and, in the original version of TORCH, PH4 (McMillan et al. 2012) + MULTIPLES (Portegies Zwart & McMillan 2018) handled the stellar dynamics.
In that version (Wall et al. 2019, 2020), TORCH could not handle the hundreds of thousands of stars that form in massive GMCs > 105 M⊙. In this work, we solve this problem by making three updates: 1) We replace the combination of the N-body code PH4 and the higher-order interactions MULTIPLES with the code PETAR (Wang et al. 2020a); (2) we agglomerate stars with masses < 4 M⊙ into summed-mass dynamic star particles with masses of ≥ 4 M⊙; and 3) we mass load the stellar winds to reduce the peak temperatures beyond their termination shocks. These modifications enabled TORCH to then model clouds with an initial mass of up to 106 M⊙ that form hundreds of thousands of individual stars.
We present simulations of star clusters forming from turbulent spherical clouds with masses of 104, 105, and 106 M⊙. Each of these clouds is almost identical in terms of their initial properties, with only mass and density scaled between them. Our study investigates whether the formation of YMCs parallels that of low-mass clusters or if it varies significantly with initial cloud mass and density.
This paper is the first in a series exploring the results of these simulations. In this paper, we describe the TORCH code, the new features integrated into TORCH for handling massive GMCs, and the initial conditions of our three clouds in Sect. 2. We analyze the time evolution of global gas and stellar properties in Sect. 3. In Sect. 4, we discuss the results of our analysis, and in Sect. 5 we conclude with a summary of the most important results. We provide a data repository containing a sampling of the simulation data corresponding to the panels in Figure 1, the HTML file of the three-dimensional interactive plot shown in Figure 2, and the code used to generate the interactive plot.
 |
Fig. 1. Slice plots of the three simulations in the x–y plane over time. The plane of the slices for a given cloud is the center of stellar mass in the final snapshot. Stellar positions are shown by white dots. The free-fall times tff are given in Table 1. The number of stars shows the amount of star particles in the domain, not the number sampled from the IMF. Due to our agglomeration of low-mass star particles, the number of stars sampled from the IMF is ∼10× greater. |
 |
Fig. 2. Still of the interactive plot of the embedded M4, M5, and M6 clusters (left to right) at 1 tff. The interactive plot file is available for download from the repository. |
2. Methods
2.1. Standard TORCH
TORCH1 is built upon the AMUSE framework, which couples multiple autonomous astrophysical codes. We chose codes that allowed efficient calculation of the disparate physical processes at work in star cluster formation.
The TORCH framework incorporates the adaptive mesh refinement MHD code FLASH v4.6.2 (Fryxell et al. 2000; Dubey et al. 2014) with a number of enhancements to the base version of FLASH. The base FLASH handles the MHD and sink particle formation and evolution. The modifications to FLASH presented in Wall et al. (2019, 2020) include heating and cooling, ionization, radiation transfer (using ray-tracing; see Baczynski et al. 2015), and feedback injection from stars. Stellar feedback is implemented in FLASH in the form of ionizing extreme ultraviolet (EUV) and non-ionizing far ultraviolet (FUV) radiation in the form of radiative heating and radiation pressure, as well as mechanical feedback from stellar winds and SNe. FUV rays are terminated when their flux drops below Fray ≤ 16.9 G0e−3.5 Av, where Av is the visual extinction and G0 is the Habing flux. This cutoff is 10× the applied background FUV field of Fext = 1.69 G0e−3.5 Av (Draine 1978). This limits the number of low energy rays on the grid for computational efficiency. We used the HLLD Riemann solver (Miyoshi & Kusano 2005) in FLASH paired with third-order piecewise parabolic method reconstruction (Colella & Woodward 1984).
To avoid artificial fragmentation, the Jeans length,
must be resolved by at least four cells (Truelove et al. 1997). We used a refinement criterion of 12 cells per Jeans length along with a derefinement criterion of 24 cells per Jeans length. As density increases during collapse, the Jeans length decreases until this criterion is no longer met at the highest level of AMR refinement. Sink particles were used to collect the gas that exceeds this density. The Truelove criterion sets the sink radius to Rsink = 2.5Δxmin and gives the sink threshold density during the entire run as
where cs was evaluated using the initial temperature of the gas. (If the gas heats during the run, the dense gas will be better resolved, making this a worst-case limit for the required density resolution.)
On each time step, the mass of gas within a distance Rsink of a sink particle that satisfies the criteria outlined in Federrath et al. (2010) is added to that sink’s mass reservoir for creating stars. When a sink forms, it randomly samples the Kroupa IMF (Kroupa 2002) and stores a long list of potential star masses to form (see also Sormani et al. 2017). Each time step, the sink forms as many stars from this mass list as possible until its current mass reservoir is depleted. It again forms one or more stars the next time it has accreted enough mass for at least the next star on the list. This is the standard stellar mass sampling method used in TORCH (Wall et al. 2019). Star positions are randomly sampled from a uniform spherical distribution within the sink’s accretion radius. Star velocities are set by the sink velocity added to an additional isotropic velocity dispersion with a Gaussian distribution having a standard deviation of the local sound speed.
Star particles are initially formed as zero-age main sequence stars, neglecting pre-main sequence evolution. Subsequent stellar evolution is tracked with SEBA (Portegies Zwart & Verbunt 1996), which passes the evolutionary properties informing stellar feedback to FLASH. The N-body dynamics of the stars are calculated using PETAR (Wang et al. 2020a), which is discussed further in the next section. Stars dynamically interact with the gas in FLASH through the AMUSE hierarchical coupling (Portegies Zwart et al. 2009) based on the gravity-bridge algorithm of Fujii et al. (2007).
2.2. PETAR N-body
TORCH was first designed to use the N-body code PH4 (McMillan et al. 2012) to handle direct stellar dynamics, paired with MULTIPLES (Portegies Zwart & McMillan 2018) to track binary orbital evolution and higher order perturbations. For TORCH runs using an initial cloud of 104 M⊙ and producing only a few thousand stars, this works well. However, the computational cost becomes unfeasible when pushing to higher initial cloud masses that produce far more than 104 stars with over a few hundred binary systems. This is because MULTIPLES is a serial Python code, so with many interacting stars computation times become impractical. To speed up TORCH, we replaced PH4 and MULTIPLES with PETAR (Wang et al. 2020a).
PETAR is a state-of-the-art gravitational dynamics code optimized for solving the stellar dynamics of systems with millions of stars. It accomplishes this by dividing gravitational interactions into three regimes: distant interactions calculated with a Barnes & Hut (1986) tree and handled by the framework for developing parallel particle simulation codes (FDPS; Iwasawa et al. 2016, 2020), nearby interactions solved with a fourth-order Hermite direct N-body integrator (Makino & Aarseth 1992), and close interactions (binaries and higher order systems/perturbations) solved using the Slow Down Algorithmic Regularization (SDAR) technique (Wang et al. 2020b). For each particle, the force from neighboring particles is solved depending on what distance regime they are in, with a mass-dependent factor to increase the distance over which massive particles are considered close neighbors. The SDAR feature for handling higher-order dynamics is the novel component of PETAR, enabling it to handle large numbers of binaries and higher order systems in parallel.
In Figure 3, we plot the wall-clock time per evolution step for each of the N-body codes considered. For reproducibility, this test was done with the parameters  ,
,  for PETAR and the stellar interaction radius
for PETAR and the stellar interaction radius  for MULTIPLES. PETAR is significantly faster and consistently performs well as the number of stars increases. The variability in the performance of PH4 and MULTIPLES is due to MULTIPLES taking longer if there are many third-body perturbations in a given step. We note that this test was done with single stars only; the scaling for a run with primordial binaries will be different.
for MULTIPLES. PETAR is significantly faster and consistently performs well as the number of stars increases. The variability in the performance of PH4 and MULTIPLES is due to MULTIPLES taking longer if there are many third-body perturbations in a given step. We note that this test was done with single stars only; the scaling for a run with primordial binaries will be different.
 |
Fig. 3. Wall-clock time for an evolution step for PETAR and PH4+MULTIPLES given the number of stars. |
When running PETAR in TORCH, the time step of the long distance particle tree must be set (dtsoft), as well as the changeover radius between direct N-body and tree method for force calculations (rout). If the user sets these two parameters, all other parameters are set automatically. In TORCH, the MHD code sets the global time step for all worker codes based on the Courant condition. The tree time step was set as the nearest power of two in code units below the requested time step, as a power of two is required by PETAR (like most N-body codes). This sets dtsoft. For M5 and M6 we set the outer radius rout to 0.001 pc, the standard value used in PETAR simulations. We used a softening length of  and a binary search radius of
and a binary search radius of  . For M4 we used a larger
. For M4 we used a larger  to ensure accurate force calculations given the small number of stars and low stellar density. This corresponds to
to ensure accurate force calculations given the small number of stars and low stellar density. This corresponds to 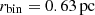 .
.
The code handling stellar mergers within PETAR is not active within the AMUSE framework, which results in star particles that approach within each others’ softening radius and should merge instead ending up with identical positions, leading to a halt in code execution. We have implemented code to check for particles in this state, and merge them. We intended to use SEBA to update the stellar mass of the surviving star, but later testing revealed that the surviving star’s mass remained unchanged. One star in the merger is removed meaning that stellar mass is unphysically lost. The effect of this error is negligible due to low merger rates: there are 0, 2, and 4 mergers in M4, M5, and M6, respectively. All of these mergers involve stars < 7 M⊙. M5 and M6 lose only 8.4 M⊙ and 22 M⊙ of stellar mass due to unphysical mergers over the course of the simulations.
2.3. Stellar modifications
We made three alterations to the star formation and evolution procedures that vary from standard TORCH to accommodate the several orders of magnitude increase in number of stars formed when increasing the initial cloud mass from 104 M⊙ to 106 M⊙.
-
m We agglomerated low-mass star particles below Magg = 4 M⊙ as they formed until their summed mass is ≥Magg. Then, a star particle is formed with a mass equal to the sum of the low-mass stars. This reduces the strain on the N-body calculations by reducing the number of dynamical star particles by 90%.
-
We mass-loaded stellar winds to raise the Courant time step by limiting the temperature of wind-blown bubbles to
 , which significantly sped up the simulations. This resulted in smaller, cooler, momentum-conserving bubbles instead of hot energy-conserving bubbles. The primary effect of wind feedback in cluster formation is to clear out extremely dense gas in order to allow ionizing radiation to form expanding H II regions. In this dense gas even hot stellar wind bubbles cool quickly, so there is little change in behavior in this regime.
, which significantly sped up the simulations. This resulted in smaller, cooler, momentum-conserving bubbles instead of hot energy-conserving bubbles. The primary effect of wind feedback in cluster formation is to clear out extremely dense gas in order to allow ionizing radiation to form expanding H II regions. In this dense gas even hot stellar wind bubbles cool quickly, so there is little change in behavior in this regime. -
We only injected feedback from stars above 20 M⊙ to reduce the cost of ray-tracing. Massive stars output most of the ionizing radiation and mechanical wind energy in clusters: by setting this limit we lost less than 20% of the total feedback energy. Stars below the feedback cutoff mass did not go SN within the time frame of our simulations (≤10 Myr).
We further explain and examine the effects of these modifications in Appendix B, including providing a quantitative analysis of the amount of total energy lost by excluding feedback for stars < 20 M⊙ in the M6 model.
2.4. Initial conditions
The initial properties of our three clouds are listed in Tables 1 and 2. We chose to keep the radius of all three clouds constant at Rcl = 11.7 pc. The radius was kept the same to have the same spatial distribution of star formation for each run. Constant radius allows the cell resolution and size of sink particles to be the same between the three simulations, and it facilitates directly comparing the morphology and dynamics of the forming clusters.
Model parameters.
Control parameters.
Consequently, the average initial densities of the clouds are 1.5, 15, and 150 M⊙ pc−3, or 10−22, 10−21, and 10−20 g cm−3. The column densities of these clouds are 2.325 × 101, 2, 3 M⊙ pc−2, respectively. Assuming a 9:1 number ratio of H:He, resulting in a mean molecular weight of μ = 1.3, this gives total particle number densities of n = 46, 460, and 4600 cm−3. Each cloud has a column density consistent with observations. Observations show a strong positive correlation between the mass and density of GMCs in PHANGS galaxies (Sun et al. 2022), suggesting mass and density should be varied together.
The initial clouds must be in pressure equilibrium with their surroundings to avoid unphysical shocks from pressure imbalances at their surfaces. The M4 and M5 clouds are in the pressure regime where there is a stable two-phase medium at solar metallicity and Milky Way background UV field (Field et al. 1969; Wolfire et al. 2003), meaning there is a set of temperatures for the cloud and background for a given cloud density where the cold dense cloud and the warm ambient medium are both in thermal equilibrium at equal pressure. The cloud temperatures for the M4 and M5 clouds are Tcl = 103 K and 28 K, respectively, and the corresponding background temperatures and number densities are Tamb = 9000 and 4000 K, and namb = 3 and 1 cm−3. The M6 cloud, however, is at a high enough pressure that a two-phase medium no longer exists. Only the cold phase can be in thermal equilibrium. This means that the low-density envelope of the M6 cloud is inherently not in thermal equilibrium. To minimize the pressure imbalance with the core, we therefore raised the background density to namb = 100 cm−3. Both the cloud and background medium for M6 are at a temperature of Tcl = Tamb = 50 K.
The initial conditions described in the rest of this section and summarized in Table 2 apply to all three clouds. The clouds have a Gaussian density profile (Bate et al. 1995; Goodwin et al. 2004) with the standard deviation set such that the ratio of the cloud’s central to edge density is 3:1. The simulation domain is a cube of half-width  with outflow boundary conditions. The outflow boundaries do allow gas flow onto the grid from ghost zones if the velocity at the edge of the grid is directed inward. The inflow of gas from the boundary is minimal: more gas exits the simulation than enters in all of our runs. Inflow was allowed, though, to prevent vacuums from forming at the boundaries. We used three refinement levels, yielding cell sizes that range from Δxmin = 0.3125 pc to Δxmax = 1.25 pc. Refinement and derefinement of the grid was determined by the Jeans criterion described in Sect. 2.1 and based on temperature and pressure gradients. The latter trigger refinement when the adapted Löhner (1987) estimator2 of temperature or pressure exceeds 0.98 and trigger derefinement when the estimators drop below 0.6. We are interested in global formation properties of clusters rather than the fragmentation of the cloud or the origin of the IMF, so we find the chosen resolution to be sufficient.
with outflow boundary conditions. The outflow boundaries do allow gas flow onto the grid from ghost zones if the velocity at the edge of the grid is directed inward. The inflow of gas from the boundary is minimal: more gas exits the simulation than enters in all of our runs. Inflow was allowed, though, to prevent vacuums from forming at the boundaries. We used three refinement levels, yielding cell sizes that range from Δxmin = 0.3125 pc to Δxmax = 1.25 pc. Refinement and derefinement of the grid was determined by the Jeans criterion described in Sect. 2.1 and based on temperature and pressure gradients. The latter trigger refinement when the adapted Löhner (1987) estimator2 of temperature or pressure exceeds 0.98 and trigger derefinement when the estimators drop below 0.6. We are interested in global formation properties of clusters rather than the fragmentation of the cloud or the origin of the IMF, so we find the chosen resolution to be sufficient.
We initially imposed a Kolmogorov (1941) turbulent velocity spectrum on all the gas in the domain. The peak Mach numbers for the turbulent spectrum are Ma = 30.3 for M6, Ma = 12.9 for M5, and Ma = 2.1 for M4. The same random seed was used to generate the turbulent velocity spectrum for all three clouds. This ensured the same turbulent collapse patterns, minimizing differences in the formation, location, and morphology of dense cores. From the edge of the cloud to the domain boundary, we linearly tapered the magnitude of the turbulent velocities from 100% to 25%. This tapering does not affect the low-density ambient background of the M4 and M5 cloud, but helps with stability in the M6 cloud by mixing the border of the cloud, where there is a small pressure jump.
The sink accretion radius and threshold density, derived in Sect. 2.1, are rsink = 2.5Δxmin = 0.78 pc and ρsink = 8.35 × 10−21 g cm−3. This gives an initial sink mass resolution of msink = 245 M⊙, meaning that when a sink initially forms it will accrete and form approximately msink worth of stellar mass, given the sink’s threshold density and accretion radius. The IMF sampling mass range is 0.08–100 M⊙. The lower end is the hydrogen-burning limit, while the upper end is the most massive star thought to form in a star cluster with stellar mass ≈104 M⊙ (Weidner et al. 2009). This is the expected stellar mass limit for a cluster similar to M4, so we chose this value as a fixed parameter for consistency between the three clusters.
The critical virial ratio for stability is αv = Ekin/|Epot| = 0.5, below which collapse occurs. Massive clouds tend to be sub-virial, with clouds of 106 M⊙ observed to have virial parameters of αv ≈ 0.05 − 0.35 (Kauffmann et al. 2013), though some surveys see super-virial massive clouds (see Fig. 2 of Chevance et al. 2023). We note that these values have been converted from the different virial parameter definition in Kauffmann et al. (2013). Therefore, we chose a fiducial virial parameter value of αv = 0.15 for our models to promote rapid onset of collapse.
Magnetic fields are prevalent in the interstellar medium (Crutcher et al. 2003) and affect the collapse of GMCs and subsequent star formation. Although they are not the dominant factor in determining how star formation proceeds within a cloud, their presence has been shown to alter the fragmentation of cores (Price & Bate 2008; Peters et al. 2011) and slow down the global evolution of the cloud (Heitsch et al. 2001). With a strong enough field, clouds can be supported against gravitational collapse (Heiles 1976), although generally observed magnetic fields are not strong enough to inhibit collapse (Klessen & Glover 2016). The critical value of the mass-to-flux ratio for a cloud to be supported by magnetic fields against gravitational collapse is given by (Mouschovias & Spitzer 1976; Mouschovias 1991)
where G is the gravitational constant and a correction factor ζ = 0.53 for a uniform sphere is used (Strittmatter 1966).
In our simulations, each cloud’s initial magnetic field  is uniform in z and decreases radially in the x–y plane, following the mid-plane density ρ(x, y, z = 0) as
is uniform in z and decreases radially in the x–y plane, following the mid-plane density ρ(x, y, z = 0) as
with 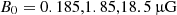 for the M4, M5, and M6 clouds, respectively. These values match observations for M5 and M6, while the field is a factor 10 weaker for M4 (Crutcher et al. 2010). The integrated magnetic flux Φ = 2πB0Rcl2/(3ln(3)), so all clouds have an initial mass-to-flux ratio Mcl/Φ = 4.5 × 104 g Gauss−1 cm−2 much larger than Equation (3). The initial magnetic fields are thus weak and do not inhibit collapse in any of our simulations.
for the M4, M5, and M6 clouds, respectively. These values match observations for M5 and M6, while the field is a factor 10 weaker for M4 (Crutcher et al. 2010). The integrated magnetic flux Φ = 2πB0Rcl2/(3ln(3)), so all clouds have an initial mass-to-flux ratio Mcl/Φ = 4.5 × 104 g Gauss−1 cm−2 much larger than Equation (3). The initial magnetic fields are thus weak and do not inhibit collapse in any of our simulations.
3. Results
3.1. Cluster formation overview
At the onset of the simulation, each cloud begins to gravitationally collapse. Turbulent velocities fragment the cloud and create overdense hubs and filaments. Because the same random seed was used in all three clouds to generate the initial turbulent velocity spectrum, the web of dense gas is the same for each cloud. This means that the spatial distribution of star formation is similar for all three clouds. This can be seen in the time evolution of the three clouds in Figure 1. The first stars all form in the largest over-density in the middle of the bottom of the cloud. Then, more stars form along the filaments of the dense cloud forming a V shape. The M5 and M6 clusters in particular look very similar in terms of sub-clustering and merging. The M4 cluster forms significantly fewer stars and therefore fewer sub-clusters.
By a free-fall time tff, the sub-clusters in M4 and M5 have mostly merged, forming a single central spherical cluster. The M6 model is still forming stars in various sub-clusters and has not assembled its main central cluster yet. By looking at the spatial distribution of sub-clusters and the density of the gas, one can see that stellar feedback becomes most efficient once the sub-clusters have merged into a single cluster. Whether feedback is only strong enough to disperse gas when clustered or this is coincidental with the timing of feedback needs further examination, but this is outside of the scope of this introductory paper. Low density bubbles begin to occupy a significant fraction of the cloud volume once the central star cluster has been assembled.
Once most of the stars have formed, the efficiency of stellar feedback for dispersing the natal gas varies greatly for the three cloud masses. The final row in Figure 1 shows the M4, M5, and M6 systems at 1.2tff. At this point, only the M4 and M5 clusters have blown large bubbles. The feedback from the M6 cluster has hardly slowed the collapse of the densest gas, and rapid star formation continues. The M4 cloud has dispersed nearly all of the remaining gas, and star formation has halted completely.
3.2. Visualizing cluster morphology
The complex 3D structure of star clusters is hard to visualize using 2D plots. Figure 2 shows a still of an interactive plot of the M4, M5, and M6 simulations after one free-fall time generated with Plotly (Plotly Technologies Inc 2015). After downloading the HTML file available in the online version of this paper, readers can zoom, pan, and rotate for a complete look at the morphology of each cluster. The color is an isosurface of the gas density in log scale, and the points are stars with sizes scaled to their stellar radius. This tool makes it clear just how non-spherical these clusters are. Comparing the still of the interactive plot to the slice plots in Figure 1, one can already extract much more information on the system’s morphology.
Zooming into the core of each cluster shows the immense stellar density of the M6 cluster, whereas in the M4 cluster one can easily distinguish individual stars. The gas is also far less dense in the M4 system compared to M5 and M6.
The shape of the M6 cluster is highly irregular. Stemming from the largest cluster, one can see a row of sub-clusters forming along a filament. Branching perpendicularly off this filamentary cluster are two more star forming filaments in a configuration resembling the letter “F”. The M5 cluster has a shape congruous to the shape of M6, but with fewer stars bridging the gaps between clusters in the main filament. The M5 cluster also has only one finger perpendicular to the main filament, which contains many fewer stars than the fingers of the M6 cluster. The M4 cluster is much less dense, with its few stars outlining the same core filament cluster seen in M5 and M6. However, in M4 sub-clusters can no longer be distinguished. The M4 sub-clusters already merged into a singular central cluster.
3.3. Star formation history
The global properties of the star clusters that form from the M4, M5, and M6 clouds over the period of star formation are shown in Figure 4 as a function of time in units of the global free-fall time of the cloud tff (see Table 1). For reference, this same figure is shown as a function of physical time in Appendix A. We analyze these properties and discuss how they compare across the three clouds to assess the effect of the initial cloud mass and density on the resultant cluster properties. Table 3 highlights the final properties of the clusters formed in the three models.
 |
Fig. 4. Global properties of the clusters and gas over time for models M4 (orange), M5 (maroon), and M6 (blue-violet) in units of free-fall time tff of the initial cloud (given in Table 1). From top left to bottom right: (a) SFR, where the transparent lines show the SFR at each star formation event, and the solid lines give the SFR smoothed using a Gaussian filter with σ = 0.005tff. (b) Instantaneous and integrated SFEs of the clouds, where ϵinst = M⋆/(Mgas + Msink + M⋆) and ϵint = M⋆/Mcloud = ϵ⋆. (c) Most massive star formed. (d) Number of formed stars. Dashed line: actual number of stars that would form from sampling the IMF given the amount of gas mass collected for star formation by sink particles. Solid line: number of stars followed in TORCH after the sampled stellar population below 4 M⊙ has been agglomerated. Dotted line: number of stars above 20 M⊙ on the grid that are generating feedback. The number of stars can drop due to SN, mass loss, or exiting the grid. (e) 3D stellar velocity dispersion. (f) Half-mass radius of the entire star cluster. (g) Total mass (dotted line), mass of stars (dashed line) and gas (solid line) on the grid. (h) Virial parameter of stars (dashed line) and gas (solid line), where αv = 0.5 is the equilibrium value. (i) Fraction of mass bound for stars (dashed line) and gas (solid line). |
Results.
Our results suggest that star formation in a GMC is a fast and efficient process regardless of initial cloud mass and density, with all three clouds converting at least 30% of their initial gas into stars within an initial free-fall time. Star formation becomes faster and more efficient as the mass and density of the GMC increases.
Stars begin forming in the M5 and M6 clouds at t = 0.3 tff, while in the M4 run it is delayed until t = 0.5 tff. Because of the turbulent field, regions of the clouds have locally shorter free-fall times leading to star formation earlier than the global free-fall time. The duration of star formation is the shortest for the M4 cloud, lasting tsf = 0.7 tff. The M5 cloud forms stars for a longer period in terms of its initial free-fall time, tsf = 1.3 tff. M6 is still forming stars 1.3 tff after the onset of SF.
The SFR (Fig. 4a) increases with cloud mass. The peak SFR for the M4, M5, and M6 clouds are SFRpeak = 0.4, 5.5, and 392 M⊙ yr−1 respectively. The average SFRs also increase with mass, with values of SFRave = 0.02, 0.06, and 1.5 M⊙ yr−1.
The integrated star formation efficiency (SFE; Fig. 4b) we discuss here is given by the ratio of stellar mass formed to the initial gas mass of the cloud ϵ⋆ = M⋆/Mcloud. The instantaneous SFE is the ratio of stars to the total mass on the grid at that point in time ϵinst = M⋆/(Mgas + Msink + M⋆).
For all three clouds, the instantaneous and integrated SFE closely follow each other at early times. In the M4 track, they diverge at t ∼ 1tff: ϵinst increases from 35 to 70%, while ϵ⋆ levels out due to gas expulsion. When all gas is fully expelled from the domain all three values will converge to ϵinst = 100%. The instantaneous SFE for M5 is beginning to increase toward 100% as the integrated SFE levels out. The ϵinst for M6, however, levels out ≈10% lower than ϵ⋆. This is due to the higher background density and some inflow from the boundary. Inflow is expected to occur for systems like M6, so this suggests observed SFEs of massive embedded clusters may be lower than the conversion ratio of gas to stars from the original cloud. For consistency, the best estimate for simulated SFE is the final integrated SFE value, and this is the value we use for all further comparisons to observations. We delve into the limitations of comparing observed and modelled SFEs in Sect. 4.1.
The M4 cloud is representative of typical GMCs at the solar circle, and its integrated SFE lies just over the top of this range at 36%. Typical SFE values of nearby clusters in the Milky Way lie between 0.1–0.3 (Lada & Lada 2003). In the higher mass clouds of M5 and M6, the SFE is much higher. The M5 cloud converted 65% of its gas into stars, and the M6 cloud converted 89% of gas into stars. This suggests that the SFE in high-mass, high-density environments can be much higher than seen in low-mass local clusters.
The free-fall time becomes so short in these high-mass clouds that the stellar feedback simply does not act quickly enough to stop star formation before most of the gas has formed into stars. Free-fall times of dense environments that are shorter than the development times for winds and SNe have indeed been shown to result in high SFE (Dekel et al. 2023). However, the more crucial factor may be that the total force budget of feedback from winds and radiation is not enough to surpass the gravity from gas and stars in dense, high-mass embedded clusters. This force-balance argument is supported by our results presented in Sect. 4.1 where the stellar feedback in a 1D model of M6 fails to expel gas from the embedded cluster’s potential well. Regardless of free-fall time, in high density clouds the total feedback energy won’t equal gravity until over half the cloud mass is converted to stars. However, if the free-fall time becomes so long ( ) that SNe become a dominant form of feedback during the primary epoch of star formation, the energy from frequent SNe may start to overpower gravity and affect the SFE. We have not explored this regime, as such a high free-fall time for a 106 M⊙ cloud is rare.
) that SNe become a dominant form of feedback during the primary epoch of star formation, the energy from frequent SNe may start to overpower gravity and affect the SFE. We have not explored this regime, as such a high free-fall time for a 106 M⊙ cloud is rare.
Figure 4c shows the mass of the most massive star that has formed from random draws from the IMF. By a free-fall time, each cloud has already formed the most massive star in its cluster. We find that the mass of the most massive star increases with cluster mass. For the M5 and M6 clouds, the most massive star is at the maximum sampling mass of 100 M⊙, while the M4 cloud’s most massive star is around 70 M⊙. This is a stochastic effect; as more stars are sampled from the IMF, you will eventually sample the most massive star in the distribution. This reproduces the effect suggested by Weidner et al. (2009) and Yan et al. (2023) that the cluster mass limits the most massive star mass. In each cloud, it is interesting to note that each instance of the formation of a very massive star, that is, above 40 M⊙, correlates with a slowing of star formation indicated by a reduction in the SFE slope.
The M6 cloud forms from IMF sampling ∼106 stars, M5 forms ∼105 stars, and M4 forms ∼104 stars, shown in Figure 4d. With agglomeration, the number of stars in the simulation are about 10% of these numbers, so the improved version of TORCH with PETAR can simulate clusters of > 105 individual stars.
3.4. Cluster evolution
The evolution of the global properties of the formed star clusters occurs quite similarly for all three clouds, but the magnitude of their values depends greatly on the cloud’s initial mass.
The stellar velocity dispersion (Fig. 4e) generally increases with initial cloud mass. The velocities of stars increase at a slow pace before leveling out after 1 tff. For the M4 cluster, the velocity dispersion levels out at just 1.0 km s−1. At late times, the velocities of the stars begin to slightly decrease in M4. This decrease correlates to the increasing half-mass radius of M4, indicating the star cluster is expanding and the stellar velocities are slowing. The M5 cluster reaches a velocity dispersion of 5 km s−1 and the M6 cluster has a velocity dispersion of 20 km s−1. The deeper potential wells of the higher mass clusters, going as the square root of the mass for these similar sized objects, drive the higher velocity dispersions, although the measured dispersion increases somewhat faster with mass than the potential well depth. In the case of M6, the potential well depth exceeds the sound speed of ionized gas, preventing gas from escaping even after ionization. For M6, the average sound speed in cells where the gas is fully ionized is cion= 16.4 km s−1.
The evolution of the half-mass radius R1/2 of all the stars in the cluster (Fig. 4f) seems to be split into a high and low-mass regime. The M5 and M6 clusters follow the same track closely. From 0.3 tff to 1.0 tff, R1/2 increases to a peak of ∼3.75 pc at ∼0.6 tff then goes down to ∼1 pc (M5) and ∼0.5 pc (M6) and begins to level out. The similarities in the evolution of the two clusters are most likely due to the fact that both clouds at early times form enough stars for distinct sub-clusters to form and merge. The sub-clusters have formed in the same places so both clusters peak at roughly the same R1/2. All of the stars in M5 and M6 remain bound, suggesting the clusters are relaxing into gravitational equilibrium. Longer runs following just the stars after gas dispersal will ultimately be needed to demonstrate this. M6 is a smaller and denser cluster than M5, likely due to the much deeper potential well of M6. Similar stellar densities are observed in the super-star clusters (SSCs) of starburst NGC 253 (Rico-Villas et al. 2020) with sizes of R < 1.7 pc and stellar masses of 104 − 6 M⊙.
The M4 cluster grows slightly differently. It increases to a peak of R1/2 = 2 pc at 1 tff, decreases to R1/2 = 1 pc, then linearly increases to 2.5 pc by 1.3 tff. The M4 cluster is expanding, but 85% of its stars remain bound, so complete dissolution has not yet occurred (Fig. 4i).
The onset and duration of gas dispersal from the star clusters depends strongly on the initial mass and density of the cloud. Figure 4g–i shows the time evolution of the mass, virial parameter, and bound mass fraction of the gas and stars. With these three plots we can track the degree of gas dispersal. From the mass plot we see that by the end of star formation, the M4 and M5 clusters have expelled a significant fraction of the initial cloud. Only 10% of the original gas mass remains in M4 and < 10% in M5. Both M4 and M5 are well on their way to full gas expulsion, as in both clusters < 10% of the gas still on the grid is bound. The gas in the M4 and M5 systems become super-virial by a free-fall time. The gas in M5 takes ∼10% longer to become unbound, but progresses identically to the M4 gas. The gas in M6 differs significantly as it remains sub-virial even beyond one free-fall time. The potential well created by the massive cluster is enough to keep the remaining gas infalling, suggesting star formation is not yet quenched in the M6 cluster.
The only star cluster that is starting to disperse is the M4 cluster (Fig. 4i). The other two star clusters remain fully bound. The stars in M5 and M6 remain sub-virial, while the stars in M4 just reach virial equilibrium by the final simulation time (Fig. 4h). The dispersal time of the gas and stars increases with initial cloud mass as there is more gravity for the stellar feedback to counteract. Although massive clusters have more stars injecting feedback, the increasing gravity overpowers the feedback. At high densities, where the potential well depth exceeds the sound speed of ionized gas, ionization feedback cannot disperse gas, while the short free-fall time assembles dense gas more quickly than feedback can work against gravity.
4. Discussion
4.1. Limitations of comparing observed and modelled star formation efficiencies
We compare the SFEs of our modelled clusters to observations by using the integrated quantity ϵ⋆, the stellar mass divided by the initial cloud mass. This is the total fraction of cloud mass that has been converted into stars. However, this value is impossible to calculate for observed clusters, as the only information available is how much gas and stars are present within a certain area. Thus, observations of star clusters only quote the instantaneous value ϵinst. There is a 3–4 order of magnitude spread in the observed SFE and SFR of Galactic GMCs (Lee et al. 2016).
A proper comparison between simulated and observed SFEs requires accounting for the amount of ongoing star formation, and determining whether the embedding gas is collapsing or dispersing. Comparisons done without accounting for the evolutionary stage of the cluster are misleading. The apparent SFE ranges from 0–100% over the lifetime of every star cluster that reaches a gas-free state, which may explain the spread in observed SFE. This issue is starting to be explored. Geen et al. (2017) suggest techniques for converting observed to integrated SFEs, although conclude that this is non-trivial and find errors up to a factor of 10. They find overall higher observed SFEs than integrated SFEs when they applied observational techniques to their simulations. On the other hand, Grudić et al. (2019) find lower observed than integrated SFEs in their models due to the inaccuracies of techniques for estimating stellar mass. One example of this comes from using only the young stellar population as a tracer for stellar mass, which underestimates the total stellar mass. They also discuss variability in observed SFEs due to the changing SFE over the course of a GMC lifetime, from first star formation to gas dispersal.
Further studies must be dedicated to outlining a systematic way to convert between observed SFEs and the final integrated SFEs we define in our models. Until then, direct comparisons should be interpreted with caution.
4.2. Observations
Galactic surveys of embedded clusters in the Milky Way typically find the SFE to be ≲30% (Lada & Lada 2003), with some studies finding lower values of ≲8% (Evans et al. 2009; Peters et al. 2011). The M4 cloud, which is a good representative of galactic GMCs3, agrees well with this SFE albeit at the high end of observed values. This could be due to the low virial parameter used, which is appropriate for M6 but lower than the average observed value of αv = 1 seen in clouds similar to M4. The missing radiative feedback from stars < 20 M⊙ could also be a factor causing the high SFE of M4 given the low-density of the cloud. Feedback contributions from low-mass stars could be a key factor in quenching star formation in Milky Way-like clouds.
The higher mass clouds similar to M5 and M6, however, have SFEs well above 30%. While there are no Milky-Way analogs to the M6 cloud, there are a few for M5. There is the W43 GMC with 1.32 × 105 M⊙ of gas within R ∼ 10 pc (Lin et al. 2016), similar to the M5 cloud with R = 11.7 pc. The W49 star forming region has a central YMC with stellar mass ≳ 5 × 104 M⊙ and gas mass ∼ 2 × 105 M⊙ and ∼ 1.1 × 106 M⊙ within 6 and 60 pc respectively (Galván-Madrid et al. 2013). This gives a current SFE of 20% in the inner region. W49 has ongoing star formation, and its embedded gas cloud is twice as massive and 15 times as dense as our M5 model. Based on our results for M5 and the fact that SFE increases with density, we predict W49 will exceed the SFE found for M5 of ϵ⋆ = 65%.
Though conditions required to form the M6 cloud are not observed in the Milky Way, they are present in other galaxies. Starburst galaxies have been observed to host SSCs with SFEs of ϵinst ≈ 50 − 80%. These SSCs cover a size and mass range comparable to our models (see Table 4).
Properties of observed super star clusters.
Additionally, the disks of gas-rich high redshift galaxies can be violently unstable and are thought to form clouds similar to M6 (see Tacconi et al. 2020). We can now directly observe the high redshift environment of forming GCs with JWST. (Li et al. 2024) predicts JWST will find feedback-free starbursts (Dekel et al. 2023), which are massive galaxies at z ≳ 10 with high SFEs due to dense gas with free-fall times ≤ 10 Myr forming stars effectively free of stellar feedback. Recent JWST observations uncovered “younger” populations of GCs in galaxies at redshift z = 0.38 (Harris & Reina-Campos 2023), and others are expected to observe GCs up to z = 1 without lensing (Reina-Campos & Harris 2024).
With lensing, clumps that are likely proto-GCs can be observed at redshift z > 1 (Adamo et al. 2023; Claeyssens et al. 2023). One such proto-GC candidate was found through lensing at z ∼ 6 with ≲ 106 M⊙ and a core radius of Rc < 13 pc (Vanzella et al. 2019). Another more massive bound YMC 3 Myr old was found at z = 2.37 with ∼ 107 M⊙, and R ∼ 8 pc (Vanzella et al. 2022a). A strongly lensed galaxy at z = 4 contains three bound YMCs each younger than < 30 Myr with masses between (0.7–4.0) × 106 M⊙ and radius estimates of 3–20 pc (Vanzella et al. 2022b). The Sunrise arc is a strongly lensed z ≈ 6 galaxy found to contain six YMCs with masses ∼ 106−7 M⊙, radii of ∼1–20 pc, and ages 1–30 Myr (Vanzella et al. 2023). Most of these recently discovered YMCs or proto-GCs are analogous in size and mass to the M6 cluster or larger. Dense regions of prolific star formation that form these objects seem pervasive in the early Universe, and more will surely be discovered as more JWST data arrives. Due to their similar properties, we argue that these clusters formed in the same manner as M6.
Another situation that can form GMCs similar to M6 is major galaxy mergers with small mass ratios. Tidal interactions of major galaxies are linked to bursts in star formation (Larson & Tinsley 1978; Lonsdale et al. 1984; Barton et al. 2000; Ellison et al. 2008; Renaud et al. 2019). Since most massive galaxies are believed to undergo at least one merger in their lifetime, this is not a rare occurrence. Galaxy mergers have been suggested as the progenitors of YMCs and younger GCs (Ashman & Zepf 1992; van den Bergh 2001). We note that this only applies to major galaxy interactions: minor galaxy interactions with large mass ratios produce little to no enhancement of the overall SFR (Cox et al. 2008; Tress et al. 2020).
In the interacting Antennae galaxies, the Firecracker cloud, which resembles M6, was observed by Whitmore et al. (2014). Finn et al. (2019) constrains its mass and characteristic radius to (1–9) × 106 M⊙ and 22 pc. The Firecracker cloud is in the very early stages of star formation, as it is estimated to have only formed M⋆ ≲ 104 M⊙. This is less than 10% of the expected stellar mass of the final star cluster (Johnson et al. 2015). These observations show that progenitor clouds similar to M6 can form before any significant amount of star formation occurs.
A survey of the molecular clouds in the Antennae galaxies done by Wei et al. (2012) revealed two populations of MCs, with a distinct break in the differential mass function at  . Clouds above this mass were found in the regions of intense star formation, while the lower mass clouds were in more dormant regions. The large velocities seen in the high SF regions suggest compression by shocks, supporting the idea that galaxy mergers lead to high-mass GMCs that become sites of extreme star formation.
. Clouds above this mass were found in the regions of intense star formation, while the lower mass clouds were in more dormant regions. The large velocities seen in the high SF regions suggest compression by shocks, supporting the idea that galaxy mergers lead to high-mass GMCs that become sites of extreme star formation.
Finn et al. (2019) measured the velocity dispersion in the Firecracker cloud and found it to be neither in virial equilibrium nor free-fall. They conclude that there must be a high pressure background to contain the gas at such high densities in equilibrium.
We compare this velocity dispersion to those in our clouds over time to test whether we reach such high velocities through the addition of stellar feedback to free-fall collapse alone or whether a high pressure background is indeed needed. The results of this comparison are shown in Figure 5. We plot the size-line width coefficient σv2/R against surface density Σ = M/πR2 for each of our clouds to compare with the observations from Finn et al. (2019). The observations are shown by the white diamonds in Figure 5 corresponding to 4 aperture sizes they used for R: 6.4, 15, 26, and 37 pc. We use four smaller aperture sizes: 5, 10, 15, and 20 pc, as our cloud is half the radius of the Firecracker. We plot four times for each of our simulations corresponding to t = 0.0, 0.5, 1.0, 1.25 tff, with a line connecting the points showing the set of apertures. The apertures for each set increase from right to left with decreasing surface density. The colors of the points indicate the amount of stellar mass formed, colored white when no SF has occurred yet. The sizes indicate the initial gas mass of the cloud, with the smallest being the M4 simulations and the largest being M6. The two labelled lines on the plot indicate the analytical conditions for free-fall and virial equilibrium (see the discussion of Fig. 2 in Ballesteros-Paredes et al. 2011). We include these lines for easier comparison to the observations presented by (Finn et al. 2019) rather than for inferring the state of the system. Unintuitively, velocity dispersions in a state of free-fall exceed those of virial equilibrium.
 |
Fig. 5. Size-line width coefficient versus surface density for the Firecracker cloud (Finn et al. 2019) and the M4, M5, and M6 clouds. The four red diamonds are observations, done using apertures (1–4) with radii R = 6.4, 15, 26, and 37 pc. The other points are our simulations, with connected points corresponding to apertures (1–4) of radii R = 5, 10, 15 and 20 pc. The colors indicate how much stellar mass has been produced (with empty points indicating no star formation). The lines correspond to virial equilibrium and free-fall as labeled (see Fig. 2 of Ballesteros-Paredes et al. 2011). |
Though the Firecracker cloud is as massive as M6, its surface density is lower: more comparable to M5. This is why we see an overlap between M5 and the Firecracker cloud when M5 has formed 4 × 104 M⊙ of stars, which is on the order of the stellar mass estimated to have already formed in the Firecracker cloud of ≤ 104 M⊙. This aligns with the idea that surface density is more influential than mass in the formation of star clusters. This also supports the possibility that the Firecracker gas velocities could be caused by the contribution of stellar feedback to the velocity dispersion in addition to free-fall collapse. The fast dynamical evolution of our models suggests that these are not equilibrium objects, making it unnecessary to invoke a high-pressure background to keep the cloud from expanding. This suggests objects like the Firecracker cloud can form from collapse with observed velocity dispersions without invoking a high pressure background medium.
4.3. Other simulations
For massive star clusters to form, they must survive the epoch of gas dispersal and remain bound. An analytical model predicts a positive correlation of SFE to SFR and initial cloud mass (Zamora-Avilés & Vázquez-Semadeni 2014). At high enough surface densities, stellar feedback cannot compete with star formation. Numerical studies done by Geyer & Burkert (2001) found that if the stars are initially in virial equilibrium with the remaining gas, only clusters with SFE ≥ 50% remain bound against the outflow of the gas. Li et al. (2018) finds in their cosmological galaxy formation models that though galactic properties are unaffected by varying ϵ⋆, the properties of star clusters are affected. In particular, they found that the initial bound fraction of stars increases with ϵ⋆ and cloud mass. Farias et al. (2023) ran cluster formation models from 2 × 104 M⊙ clouds and finds that SFE and gas expulsion time correlate with global bound fraction, with all SFEs ≤ 20% and all bound fractions ≤40%. Although it is still possible to form bound clusters with low SFE, these studies imply massive bound star clusters were most likely formed with high SFEs.
Menon et al. (2023) also finds high SFEs of ∼80% for 106 M⊙ clouds with feedback in the form of radiation pressure solved using a variable Eddington tensor approach as opposed to our ray-tracing method. In this density regime, radiation pressure is the dominant feedback mechanism4. They conclude that radiation pressure simply cannot regulate star formation for clouds with surface densities Σ ≳ 103 M⊙ pc−2.
Our results are more constraining: We included more feedback physics, and we still achieved SFEs of ϵ⋆ > 80%. Our M6 cloud is above this surface density with Σ = 2.3 × 103 M⊙ pc−2. They also tested a larger 106 M⊙ cloud with roughly the same surface density as our M5 cloud, and find an SFE of ϵ⋆ ≈ 60% comparable to the SFE of our M5 cluster of ϵ⋆ = 65%.
Other simulations of massive star cluster formation with initial cloud mass of 106 M⊙ find high SFEs of ∼65% (Grudić et al. 2018) and 38% (Kim et al. 2018) for surface densities of 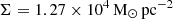 and
and  , respectively. Kim et al. (2018) finds an even higher SFE of 51% for a 105 M⊙ cloud but with a surface density of
, respectively. Kim et al. (2018) finds an even higher SFE of 51% for a 105 M⊙ cloud but with a surface density of  . Cluster models in Kimm et al. (2022) reached ϵ⋆ = 50–72% from an initial cloud of 1.4 × 106 M⊙ and
. Cluster models in Kimm et al. (2022) reached ϵ⋆ = 50–72% from an initial cloud of 1.4 × 106 M⊙ and  despite SN and radiation feedback. Another cluster, modeled with radiation feedback by Fukushima & Yajima (2021), reached ϵ⋆ = 78% from a 106 M⊙ cloud with
despite SN and radiation feedback. Another cluster, modeled with radiation feedback by Fukushima & Yajima (2021), reached ϵ⋆ = 78% from a 106 M⊙ cloud with  . This study also finds that bound cluster formation only occurs with ϵ⋆ ≥ 30%. Recent models of
. This study also finds that bound cluster formation only occurs with ϵ⋆ ≥ 30%. Recent models of  clouds with R = 10 pc, αv = 0.1, and Z = 0.2 Z⊙ reached ϵ⋆ = 50% (Fujii et al. 2024). The SFE in all of these studies increases strongly with surface density and slightly with initial cloud mass. Our results combined with those from previous models provide evidence that the formation of bound YMCs requires not only a high cloud mass but also, and more importantly, a high surface density.
clouds with R = 10 pc, αv = 0.1, and Z = 0.2 Z⊙ reached ϵ⋆ = 50% (Fujii et al. 2024). The SFE in all of these studies increases strongly with surface density and slightly with initial cloud mass. Our results combined with those from previous models provide evidence that the formation of bound YMCs requires not only a high cloud mass but also, and more importantly, a high surface density.
Simulations of star clusters forming from clouds similar to our M5 cloud resulted in lower SFEs of 10–30%. The main difference between these models and ours is the use of sink particles to represent sub-clusters with combined feedback compared to our tracking of feedback from individual massive stars. A cloud modelled by He et al. (2019) with an initial mass of 105 M⊙, peak number density  , metallicity
, metallicity 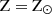 , a higher virial parameter αv = 0.4, and stellar feedback only through UV radiation reached a SFE of 13.7% by 6 tff. The cloud in Ali (2021) is the same mass and metallicity as M5, almost the same radius,
, a higher virial parameter αv = 0.4, and stellar feedback only through UV radiation reached a SFE of 13.7% by 6 tff. The cloud in Ali (2021) is the same mass and metallicity as M5, almost the same radius,  , but is initially super-virial, with αv = 1. By 0.75 tff, the SFE reached only 10% while M5 reached ϵ⋆ = 20% by this time. This difference may come from the different initial virial parameters, which prolongs the formation of the cluster in Ali (2021). Another possible cause is different feedback models. Injecting stellar feedback from entire sub-clusters rather than individual stars could artificially strengthen the effect of feedback resulting in a lower SFE.
, but is initially super-virial, with αv = 1. By 0.75 tff, the SFE reached only 10% while M5 reached ϵ⋆ = 20% by this time. This difference may come from the different initial virial parameters, which prolongs the formation of the cluster in Ali (2021). Another possible cause is different feedback models. Injecting stellar feedback from entire sub-clusters rather than individual stars could artificially strengthen the effect of feedback resulting in a lower SFE.
Fujii et al. (2021) presents star-by-star cluster models with feedback in the form of radiation, radiation pressure and stellar outflows. For an initial cloud of  ,
,  , and αv = 0.25 they find ϵ⋆ = 40%. The same cloud with a larger virial parameter of αv = 1.0 only reached ϵ⋆ = 40%. Their sub-virial model agrees with our findings for M5. The super-virial model with a lower SFE further indicates that the high SFEs we find are possibly due to the low initial virial parameter, particularly for lower density clouds.
, and αv = 0.25 they find ϵ⋆ = 40%. The same cloud with a larger virial parameter of αv = 1.0 only reached ϵ⋆ = 40%. Their sub-virial model agrees with our findings for M5. The super-virial model with a lower SFE further indicates that the high SFEs we find are possibly due to the low initial virial parameter, particularly for lower density clouds.
A colliding flow model of star formation in GMC environments described in Colín et al. (2013a) with individual star formation and ionizing radiation found SFEs of ϵ⋆ = 10–30% depending on the degree of concentration by the flows. The two cylindrical streams were very large, with r = 64 pc and  and rarefied, with
and rarefied, with  , with the total mass in the two streams equalling 9 × 105 M⊙. The different initial conditions hinder a direct comparison to our SFE values, but reaching high SFEs from low density flows aligns with our results for M4.
, with the total mass in the two streams equalling 9 × 105 M⊙. The different initial conditions hinder a direct comparison to our SFE values, but reaching high SFEs from low density flows aligns with our results for M4.
Simulations have broadly found star formation to be suppressed with each additional form of stellar feedback included in the model (see Dale 2015). The exclusion of protostellar jets in our feedback model may artificially raise the SFR, as they contribute to the dispersal of gas around even low-mass stars at small scales (Chevance et al. 2023). Due to the quantity of low-mass stars and the collimated shape of the outflow, jets are drivers of turbulence at large scales in GMCs (e.g., Nakamura & Li 2007; Federrath 2015; Appel et al. 2022). These models do show that jets are an important factor in slowing the growth rate of the integrated SFE, though the final SFE is not known due to the duration of the simulations (Federrath 2015). Guszejnov et al. (2021) performed simulations of star-by-star cluster formation from 2 × 104 M⊙ clouds with stellar feedback, including protostellar jets as well as radiation, winds, and SNe. Simulations were repeated that isolated each form of feedback. They found jets to be important in regulating the growth of low-mass stars and constraining the IMF. Radiation and jets were the primary form of feedback that slowed star formation and dispersed the cloud. However, again the simulations were not run until the end of star formation, so the degree to which each effect changes the final SFE remains uncertain.
Despite their ubiquity, jets cannot prevent gas in high-density GMCs from forming stars eventually nor contain the power needed to disperse GMCs (see Chevance et al. 2023). The effect that jets would have on more massive clouds remains unclear. Although they may indeed slow star formation to observed values, as proposed by Chevance et al. (2023), analytic work by Matzner (2002) suggests that more massive clouds would be resistant to dispersal by jets, consistent with simulations by Guszejnov et al. (2022).
In order to verify the physical plausibility of the high SFE in M6 despite the large number of formed stars, we have directly compared our 3D results to a followup calculation using the one-dimensional (1D) code Winds And Radiation Pressure: Feedback Induced Expansion, colLapse and Dissolution (WARPFIELD; Rahner et al. 2019). This code models the effect of stellar feedback from young clusters on their natal gas cloud in spherical symmetry. WARPFIELD is designed to solve for the self-consistent motion of a 1D spherical gas shell evolving under the influence of feedback mechanisms including stellar winds, SNe, and radiation pressure, with consideration of gravity. We ran WARPFIELD using the same initial conditions as chosen for the M6 run (i.e., mass, density, temperature), with the addition that we varied the SFE from ϵ⋆ = 0.1–0.9 in bins of 0.1, as shown in Figure 6. This varies the strength of the stellar feedback to test whether the M6 cloud would still be stable given amount of stars formed.
 |
Fig. 6. WARPFIELD evolution of shell radius versus time with different initial SFEs with the same parameters described in M6. In all cases, stellar feedback is inefficient in dispersing the surrounding dense cloud, and the shell eventually undergoes re-collapse. |
For all SFE values, the shocked gas eventually re-collapses. At this high density, the included feedback is not strong enough to completely disperse the cloud. The SFE of our M6 cluster most closely resembles the WARPFIELD runs with ϵ⋆ = 80% & 90% in Figure 6. The WARPFIELD model reaches a maximum radius of  at
at  , and collapses back to
, and collapses back to  by
by  . In the 1D model, all feedback occurs at a single point, so it is more effective than in our star-by-star 3D model, as in multiple dimensions channels that vent thermal energy can exist. Nevertheless, the gas still re-collapses, promoting further star formation. The expanding gas is not accelerated fast enough to escape the deep potential well of the massive cloud and the cluster that forms from it. This result supports the idea that the high SFE is due to the total feedback strength being weaker than gravity at these densities.
. In the 1D model, all feedback occurs at a single point, so it is more effective than in our star-by-star 3D model, as in multiple dimensions channels that vent thermal energy can exist. Nevertheless, the gas still re-collapses, promoting further star formation. The expanding gas is not accelerated fast enough to escape the deep potential well of the massive cloud and the cluster that forms from it. This result supports the idea that the high SFE is due to the total feedback strength being weaker than gravity at these densities.
However, our results do suggest that more dispersed star formation leading to increased energy dissipation by radiative cooling may not even allow that much expansion. To resolve SFE well, feedback must be modelled for individual stars instead of for entire clusters. Approximating feedback as a sum for an entire cluster underestimates the SFE.
5. Conclusions
We performed numerical simulations of star cluster formation from gas clouds that run until star formation ceases or slows significantly due to stellar feedback dispersing any remaining gas. We tested initial cloud masses of 104, 105, and 106 M⊙ with radius R = 11.7 pc, holding all other characteristics of the initial cloud and simulation parameters the same. We analyzed the star formation histories and followed the evolution of the gas and forming star clusters. From this study, we conclude the following:
-
Giant molecular clouds with surface density
 and mass
and mass  can form fully bound star clusters with stellar mass
can form fully bound star clusters with stellar mass  with a high SFE ϵ⋆ ≥ 65% over a short time tsf ≈ 1tff, as seen by M5 and M6. The lower mass and density M4 cloud forms a cluster with a lower bound mass fraction of 60%.
with a high SFE ϵ⋆ ≥ 65% over a short time tsf ≈ 1tff, as seen by M5 and M6. The lower mass and density M4 cloud forms a cluster with a lower bound mass fraction of 60%. -
The Firecracker cloud in the Antennae galaxies, with a mass of 1–9
 and a radius of
and a radius of 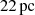 (Finn et al. 2019), is a close analog to our M6 cloud, though with a surface density more closely matching our M5 cloud. From our results we can estimate that the Firecracker cloud will convert 65–85% of its mass into stars within a free-fall time and that it will form a YMC.
(Finn et al. 2019), is a close analog to our M6 cloud, though with a surface density more closely matching our M5 cloud. From our results we can estimate that the Firecracker cloud will convert 65–85% of its mass into stars within a free-fall time and that it will form a YMC. -
It has been suggested that the Firecracker cloud must be surrounded by a high pressure medium to contain it because of its high surface density and size-line width coefficient σv2/R (Johnson et al. 2015; Finn et al. 2019). However, the M5 cluster reaches the same values by the time it forms
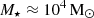 worth of stars, the same amount of stellar mass estimated to have formed in the Firecracker cloud. This suggests another possibility: Rather than being an equilibrium object confined in a high pressure environment, the Firecracker cloud is actually dynamically collapsing and forming stars, and the high velocity dispersion of the gas is from the combination of free-fall collapse and stellar feedback.
worth of stars, the same amount of stellar mass estimated to have formed in the Firecracker cloud. This suggests another possibility: Rather than being an equilibrium object confined in a high pressure environment, the Firecracker cloud is actually dynamically collapsing and forming stars, and the high velocity dispersion of the gas is from the combination of free-fall collapse and stellar feedback. -
Star formation from GMCs is capable of achieving up to 85% efficiency at high densities. Our M6 cloud is the most efficient of our models, converting ϵ⋆ = 85% of its gas into stars. Even with hundreds of massive stars producing feedback, the short timescale of gravitational collapse for dense massive clouds renders the stellar feedback inefficient at slowing early star formation. However, even at much lower densities and masses, the M5 and M4 clouds achieved high SFEs of ϵ⋆ = 65% and 36%, respectively. In dense, massive clouds, the total dispersing force of stellar feedback from winds and radiation cannot counteract the gravity from stars and gas until over half the cloud mass is converted into stars.
-
The M4 cloud has a typical mass and size of Milky-Way GMCs. The SFE of M4 matches the maximum observed SFE values. This high SFE could be because of the low initial virial parameter of the cloud, or it could be due to the missing FUV radiation from stars
 . Alternatively, the exclusion of the protostellar jet feedback mechanism may be important for clouds similar to M4 clouds, as suggested, for example, by Chevance et al. (2023). Further studies must be done to constrain the effect of varying the virial parameter and including protostellar jets on integrated SFE.
. Alternatively, the exclusion of the protostellar jet feedback mechanism may be important for clouds similar to M4 clouds, as suggested, for example, by Chevance et al. (2023). Further studies must be done to constrain the effect of varying the virial parameter and including protostellar jets on integrated SFE. -
Star formation is fast in our models of clouds with low αv. Regardless of the initial mass or density, the majority of star formation occurs within the first global free-fall time of the collapsing GMC. Collapse occurs and stars are produced so rapidly that stellar feedback is only prevalent and strong enough to clear dense gas from the cluster’s deep potential well after most of the cloud has formed into stars. The speed of star formation may depend strongly on the initial virial parameter and the inclusion of jets.
-
A 1D stellar feedback model WARPFIELD was run using the same mass and density as the M6 simulation. In it, the gas re-collapses even for SFEs up to 90%. Even centralized feedback cannot expel the gas from the potential well of the massive cluster that forms. The WARPFIELD results indicate that the expanding gas shell for ϵ⋆ = 85% collapses back to R = 0 by 11 Myr.
-
Including feedback for individual stars rather than adding the total energy for the cluster at a single point is important for correctly constraining star formation histories. Modelling individual stellar feedback spreads the feedback energy enough to greatly reduce its effectiveness at clearing the natal gas because of the resulting enhanced radiative cooling. Models that add stellar feedback for the entire star cluster at a single point appear to overestimate the effect of the feedback on the gas and the star formation timescale and to underestimate the final SFE.
In conclusion, bound massive star clusters such as YMCs and GCs readily form from high-mass, dense GMCs. The GMCs can become this dense and massive naturally, even in the present day, as shown by the Firecracker cloud in the Antennae galaxies. In the early Universe, where galaxies were much more gravitationally unstable, these conditions would be much more common. The subsequent star formation from these dense high-mass clouds is highly efficient, converting ≥40% of the gas mass into stars within the first free-fall time of the initial cloud. The short timescales of star formation and/or the deep gravitational potential wells of dense, massive clouds render stellar feedback unable to significantly slow star formation, leading to integrated efficiencies as high as 85% for more massive clouds. After their formation, the clusters born in these environments remain bound after 90% of the gas is expelled.
Until recently, directly observing proto-GCs has been elusive. Now with JWST, observers have discovered five bound stellar clumps just  after the Big Bang at
after the Big Bang at  (Adamo et al. 2024). These clusters in the strongly lensed galaxy SPT0615-JD1 (alias the Cosmic Gems arc) have intrinsic masses of
(Adamo et al. 2024). These clusters in the strongly lensed galaxy SPT0615-JD1 (alias the Cosmic Gems arc) have intrinsic masses of 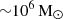 , half-light radii of
, half-light radii of 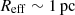 , and ages between 9 and 35 Myr. Roughly ∼60% of the total F150W flux of the galaxy comes from these five clusters, indicating that the predominant mode of star formation in these systems occurs in massive clusters. The resemblance between M6 and these objects is notable, indicating that the mode of star formation described in this study is a probable path for the formation of YMCs and proto-GCs in the present and early Universe, respectively.
, and ages between 9 and 35 Myr. Roughly ∼60% of the total F150W flux of the galaxy comes from these five clusters, indicating that the predominant mode of star formation in these systems occurs in massive clusters. The resemblance between M6 and these objects is notable, indicating that the mode of star formation described in this study is a probable path for the formation of YMCs and proto-GCs in the present and early Universe, respectively.
Data availability
Simulation data and the interactive plot file is available for download at https://doi.org/10.5531/sd.astro.8.
TORCH version used for this work: https://bitbucket.org/torch-sf/torch/commits/tag/massive-cluster-1.0
See Rice et al. (2016) for a catalog of Milky-Way molecular cloud properties.
See extended data Figure 5 of Howard et al. (2018) and Figure 12 of Krumholz et al. (2019).
Acknowledgments
B.P. would like to thank Gastón Escobar and Michela Mapelli for the helpful discussions that led to solving a persistent bug allowing continuation of the simulations. B.P. thanks Shyam Menon for many fruitful discussions of YMC formation, particularly regarding the battle between stellar feedback and gravity. We thank the referee for their useful comments and insights. B.P. was partly supported by a fellowship from the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg (IMPRS-HD). M.-M.M.L., B.P., E.P.A., and A.T. were partly supported by NSF grants AST18-15461 and AST23-07950. C.C.-C. is supported by a Canada Graduate Scholarship - Doctoral (CGS D) from the Natural Sciences and Engineering Research Council of Canada (NSERC). This work used Stampede 2 at TACC through allocation PHY220160 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants 21-38259, 21-38286, 21-38307, 21-37603, and 21-38296. The code development that facilitated this study was done on Snellius through the Dutch National Supercomputing Center SURF grants 15220 and 2023/ENW/01498863. S.A. acknowledges the support of NSF grant AST-2009679. M.W. acknowledges the support of NOVA project 10.2.5.12. R.S.K. and S.C.O.G. acknowledge financial support from the European Research Council via the ERC Synergy Grant “ECOGAL” (project ID 855130), from the Heidelberg Cluster of Excellence (EXC 2181 – 390900948) “STRUCTURES”, funded by the German Excellence Strategy, and from the German Ministry for Economic Affairs and Climate Action in project “MAINN” (funding ID 50OO2206). The team in Heidelberg also thanks The Länd and the German Science Foundation (DFG) for computing resources provided in bwHPC supported by grant INST 35/1134-1 FUGG and for data storage at SDS@hd supported by grant INST 35/1314-1 FUGG. L.W. thanks the National Natural Science Foundation of China for support through grants 21BAA00619, 12073090 and 12233013, and the one-hundred-talent project of Sun Yat-sen University, the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (22hytd09). The authors acknowledge Interstellar Institute’s program “II6” and the Paris-Saclay University’s Institut Pascal for hosting discussions that nourished the development of the ideas behind this work.
References
- Adamo, A., Zeidler, P., Kruijssen, J. M. D., et al. 2020, Space Sci. Rev., 216, 69 [Google Scholar]
- Adamo, A., Usher, C., Pfeffer, J., & Claeyssens, A. 2023, MNRAS, 525, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Bradley, L. D., Vanzella, E., et al. 2024, Nature, 632, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Ali, A. A. 2021, MNRAS, 501, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, E. P., Mac Low, M.-M., Agertz, O., Renaud, F., & Li, H. 2024, A&A, 681, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appel, S. M., Burkhart, B., Semenov, V. A., Federrath, C., & Rosen, A. L. 2022, ApJ, 927, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Arthur, S. J. 2007, Astrophys. Space Sci. Proc., 1, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Arthur, S. J., Dyson, J. E., & Hartquist, T. W. 1993, MNRAS, 261, 425 [CrossRef] [Google Scholar]
- Arthur, S. J., Henney, W. J., & Dyson, J. E. 1996, A&A, 313, 897 [NASA ADS] [Google Scholar]
- Ashman, K. M., & Zepf, S. E. 1992, ApJ, 384, 50 [Google Scholar]
- Baczynski, C., Glover, S. C. O., & Klessen, R. S. 2015, MNRAS, 454, 380 [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Hartmann, L. W., Vázquez-Semadeni, E., Heitsch, F., & Zamora-Avilés, M. A. 2011, MNRAS, 411, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Barton, E. J., Geller, M. J., & Kenyon, S. J. 2000, ApJ, 530, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [Google Scholar]
- Bochkarev, N. G. 1988, Nature, 332, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [Google Scholar]
- Chevance, M., Krumholz, M. R., McLeod, A. F., et al. 2023, ASP Conf. Ser., 534, 1 [NASA ADS] [Google Scholar]
- Chu, Y.-H., Guerrero, M. A., Gruendl, R. A., García-Segura, G., & Wendker, H. J. 2003, ApJ, 599, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Claeyssens, A., Adamo, A., Richard, J., et al. 2023, MNRAS, 520, 2180 [NASA ADS] [CrossRef] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Colín, P., Vázquez-Semadeni, E., & Gómez, G. C. 2013a, MNRAS, 435, 1701 [CrossRef] [Google Scholar]
- Cournoyer-Cloutier, C., Tran, A., Lewis, S., et al. 2021, MNRAS, 501, 4464 [NASA ADS] [CrossRef] [Google Scholar]
- Cournoyer-Cloutier, C., Sills, A., Harris, W. E., et al. 2023, MNRAS, 521, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, T. J., Jonsson, P., Somerville, R. S., Primack, J. R., & Dekel, A. 2008, MNRAS, 384, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R., Heiles, C., & Troland, T. 2003, Lect. Notes Phys., 614, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E. 2015, New Astron. Rev., 68, 1 [CrossRef] [Google Scholar]
- Dale, J. E., Bonnell, I. A., Clarke, C. J., & Bate, M. R. 2005, MNRAS, 358, 291 [CrossRef] [Google Scholar]
- Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Li, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [Google Scholar]
- Dubey, A., Antypas, K., Calder, A. C., et al. 2014, Int. J. High Perf. Comput. Appl., 28, 225 [CrossRef] [Google Scholar]
- Dyson, J. E., & Hartquist, T. W. 1992, Astrophys. Lett. Commun., 28, 301 [NASA ADS] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, AJ, 135, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Emig, K. L., Bolatto, A. D., Leroy, A. K., et al. 2020, ApJ, 903, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J. I., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M. 2006, ApJ, 652, 1129 [CrossRef] [Google Scholar]
- Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., Chandar, R., & Whitmore, B. C. 2005, ApJ, 631, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Farias, J. P., Offner, S. S. R., Grudić, M. Y., et al. 2023, MNRAS, 527, 6732 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C. 2015, MNRAS, 450, 4035 [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P. C., & Klessen, R. S. 2010, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Finn, M. K., Johnson, K. E., Brogan, C. L., et al. 2019, ApJ, 874, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJs, 131, 273 [CrossRef] [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2011, Science, 334, 1380 [Google Scholar]
- Fujii, M., Iwasawa, M., Funato, Y., & Makino, J. 2007, PASJ, 59, 1095 [NASA ADS] [Google Scholar]
- Fujii, M. S., Saitoh, T. R., Hirai, Y., & Wang, L. 2021, PASJ, 73, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Hattori, K., Wang, L., et al. 2022a, MNRAS, 514, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Wang, L., Hirai, Y., et al. 2022b, MNRAS, 514, 2513 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Wang, L., Tanikawa, A., Hirai, Y., & Saitoh, T. R. 2024, Science, 384, 1488 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, H., & Yajima, H. 2021, MNRAS, 506, 5512 [NASA ADS] [CrossRef] [Google Scholar]
- Galván-Madrid, R., Liu, H. B., Zhang, Z. Y., et al. 2013, ApJ, 779, 121 [CrossRef] [Google Scholar]
- Geen, S., Soler, J. D., & Hennebelle, P. 2017, MNRAS, 471, 4844 [NASA ADS] [CrossRef] [Google Scholar]
- Geyer, M. P., & Burkert, A. 2001, MNRAS, 323, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Offner, S. S. R., Kritsuk, A. G., et al. 2020, Space Sci. Rev., 216, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., Whitworth, A. P., & Ward-Thompson, D. 2004, A&A, 414, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grudić, M. Y., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2018, MNRAS, 475, 3511 [CrossRef] [Google Scholar]
- Grudić, M. Y., Hopkins, P. F., Lee, E. J., et al. 2019, MNRAS, 488, 1501 [CrossRef] [Google Scholar]
- Grudić, M. Y., Guszejnov, D., Hopkins, P. F., Offner, S. S. R., & Faucher-Giguère, C.-A. 2021, MNRAS, 506, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Grudić, M. Y., Hopkins, P. F., Offner, S. S. R., & Faucher-Giguère, C.-A. 2021, MNRAS, 502, 3646 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Grudić, M. Y., Offner, S. S. R., et al. 2022, MNRAS, 515, 4929 [Google Scholar]
- Harris, W. E., & Reina-Campos, M. 2023, MNRAS, 526, 2696 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., & Dyson, J. E. 1996, Ap&SS, 245, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., Dyson, J. E., Pettini, M., & Smith, L. J. 1986, MNRAS, 221, 715 [NASA ADS] [CrossRef] [Google Scholar]
- He, C.-C., Ricotti, M., & Geen, S. 2019, MNRAS, 489, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1976, ARA&A, 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Mac Low, M.-M., & Klessen, R. S. 2001, ApJ, 547, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, C. S., Pudritz, R. E., & Harris, W. E. 2017, MNRAS, 470, 3346 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, C. S., Pudritz, R. E., & Harris, W. E. 2018, Nat. Astron., 2, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, M., Tanikawa, A., Hosono, N., et al. 2016, PASJ, 68, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, M., Namekata, D., Nitadori, K., et al. 2020, PASJ, 72, 13 [CrossRef] [Google Scholar]
- Johnson, K. E., Leroy, A. K., Indebetouw, R., et al. 2015, ApJ, 806, 35 [Google Scholar]
- Kauffmann, J., Pillai, T., & Goldsmith, P. F. 2013, ApJ, 779, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Kim, W.-T., Ostriker, E. C., & Skinner, M. A. 2017, ApJ, 851, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2018, ApJ, 859, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kimm, T., Bieri, R., Geen, S., et al. 2022, ApJS, 259, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, Saas-Fee Adv. Course, 43, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Krause, M. G. H., Offner, S. S. R., Charbonnel, C., et al. 2020, Space Sci. Rev., 216, 64 [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., & Puls, J. 2000, ARA&A, 38, 613 [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [Google Scholar]
- Lahén, N., Naab, T., Johansson, P. H., et al. 2019, ApJ, 879, L18 [CrossRef] [Google Scholar]
- Lahén, N., Naab, T., & Szécsi, D. 2024, MNRAS, 530, 645 [CrossRef] [Google Scholar]
- Lancaster, L., Ostriker, E. C., Kim, J.-G., & Kim, C.-G. 2021, ApJ, 914, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [Google Scholar]
- Larson, R. B., & Tinsley, B. M. 1978, ApJ, 219, 46 [Google Scholar]
- Lee, E. J., Miville-Deschênes, M.-A., & Murray, N. W. 2016, ApJ, 833, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A. D., Ostriker, E. C., et al. 2018, ApJ, 869, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, S. C., McMillan, S. L. W., Low, M.-M. M., et al. 2023, ApJ, 944, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Gnedin, O. Y., & Gnedin, N. Y. 2018, ApJ, 861, 107 [Google Scholar]
- Li, H., Vogelsberger, M., Marinacci, F., & Gnedin, O. Y. 2019, MNRAS, 487, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Dekel, A., Sarkar, K. C., et al. 2024, A&A, accepted [Google Scholar]
- Lin, Y., Liu, H. B., Li, D., et al. 2016, ApJ, 828, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Löhner, R. 1987, Comput. Methods Appl. Mech. Eng., 61, 323 [CrossRef] [Google Scholar]
- Lonsdale, C. J., Persson, S. E., & Matthews, K. 1984, ApJ, 287, 95 [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [Google Scholar]
- Makino, J., & Aarseth, S. J. 1992, PASJ, 44, 141 [NASA ADS] [Google Scholar]
- Matzner, C. D. 2002, ApJ, 566, 302 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [Google Scholar]
- McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [CrossRef] [Google Scholar]
- McMillan, S., Portegies Zwart, S., van Elteren, A., & Whitehead, A. 2012, ASP Conf. Ser., 453, 129 [NASA ADS] [Google Scholar]
- Menon, S. H., Federrath, C., & Krumholz, M. R. 2023, MNRAS, 521, 5160 [NASA ADS] [CrossRef] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C. 1991, Cosmic Magnetism and the Basic Physics of the Early Stages of Star Formation (Dordrecht: Springer, Netherlands), 61 [Google Scholar]
- Mouschovias, T. C., & Spitzer, L., Jr 1976, ApJ, 210, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Rahman, M. 2009, ApJ, 709, 424 [Google Scholar]
- Nakamura, F., & Li, Z.-Y. 2007, ApJ, 662, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., & Mac Low, M.-M. 2011, ApJ, 729, 72 [Google Scholar]
- Pittard, J. M., Hartquist, T. W., & Dyson, J. E. 2001, A&A, 373, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plotly Technologies Inc 2015, Collaborative Data Cience (Montreal, QC: Plotly Technologies Inc.) [Google Scholar]
- Portegies Zwart, S., & McMillan, S. 2018, Astrophysical Recipes (IOP Publishing), 2514 [Google Scholar]
- Portegies Zwart, S. F., & Verbunt, F. 1996, A&A, 309, 179 [NASA ADS] [Google Scholar]
- Portegies Zwart, S., McMillan, S., Harfst, S., et al. 2009, Nat. Astron., 14, 369 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2008, MNRAS, 385, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2019, MNRAS, 483, 2547 [NASA ADS] [CrossRef] [Google Scholar]
- Reina-Campos, M., & Harris, W. E. 2024, MNRAS, 531, 4099 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F. 2020, in Star Clusters: From the Milky Way to the Early Universe, eds. A. Bragaglia, M. Davies, A. Sills, & E. Vesperini, 351, 40 [NASA ADS] [Google Scholar]
- Renaud, F., Agertz, O., & Gieles, M. 2017, MNRAS, 465, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Agertz, O., et al. 2019, A&A, 625, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, T. S., Goodman, A. A., Bergin, E. A., Beaumont, C., & Dame, T. M. 2016, ApJ, 822, 52 [Google Scholar]
- Rico-Villas, F., Martín-Pintado, J., González-Alfonso, E., Martín, S., & Rivilla, V. M. 2020, MNRAS, 491, 4573 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C. M., Bryan, G. L., Hummels, C., & Ostriker, J. P. 2015, ApJ, 809, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Pettini, M., Dyson, J. E., & Hartquist, T. W. 1984, MNRAS, 211, 679 [NASA ADS] [Google Scholar]
- Sormani, M. C., Treß, R. G., Klessen, R. S., & Glover, S. C. O. 2017, MNRAS, 466, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Strittmatter, P. A. 1966, MNRAS, 132, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K.-Y., Hopkins, P. F., Hayward, C. C., et al. 2018, MNRAS, 480, 1666 [NASA ADS] [Google Scholar]
- Sun, J., Leroy, A. K., Rosolowsky, E., et al. 2022, AJ, 164, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Tress, R. G., Smith, R. J., Sormani, M. C., et al. 2020, MNRAS, 492, 2973 [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1997, ApJ, 489, L179 [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., Benford, D. J., et al. 2015, Nature, 519, 331 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 2001, ApJ, 559, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Calura, F., Meneghetti, M., et al. 2019, MNRAS, 483, 3618 [Google Scholar]
- Vanzella, E., Castellano, M., Bergamini, P., et al. 2022a, A&A, 659, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzella, E., Castellano, M., Bergamini, P., et al. 2022b, ApJ, 940, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Claeyssens, A., Welch, B., et al. 2023, ApJ, 945, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [Google Scholar]
- Wall, J. E., McMillan, S. L. W., Mac Low, M.-M., Klessen, R. S., & Portegies Zwart, S. 2019, ApJ, 887, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Wall, J. E., Mac Low, M.-M., McMillan, S. L. W., et al. 2020, ApJ, 904, 192 [Google Scholar]
- Wang, L., Iwasawa, M., Nitadori, K., & Makino, J. 2020a, MNRAS, 497, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Nitadori, K., & Makino, J. 2020b, MNRAS, 493, 3398 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
- Wei, L. H., Keto, E., & Ho, L. C. 2012, ApJ, 750, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Bonnell, I. A. D. 2009, MNRAS, 401, 275 [Google Scholar]
- Whitmore, B. C., Brogan, C., Chandar, R., et al. 2014, ApJ, 795, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C., Chandar, R., Rodríguez, M. J., et al. 2023, ApJ, 944, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, M. J. C., Portegies Zwart, S., Cournoyer-Cloutier, C., et al. 2023, MNRAS, 520, 5331 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [Google Scholar]
- Wrigge, M. 1999, A&A, 343, 599 [NASA ADS] [Google Scholar]
- Wrigge, M., Wendker, H. J., & Wisotzki, L. 1994, A&A, 286, 219 [NASA ADS] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2023, A&A, 670, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zamora-Avilés, M., & Vázquez-Semadeni, E. 2014, ApJ, 793, 84 [Google Scholar]
Appendix A: Stellar properties: Physical times
Figure A.1 reproduces Figure 4 using physical time rather than free-fall times to show global stellar properties over time. This demonstrates how much the duration of star formation shortens while its intensity increases as the cloud mass increases.
 |
Fig. A.1. Global properties of the clusters and gas over time for models M4 (orange), M5 (maroon), and M6 (blue-violet) for comparison to Figure 4, where units of free-fall time (see Table 1) are used. From top left to bottom right: (a) SFR, where the transparent lines show the SFR at each star formation event, and the solid lines give the SFR smoothed using a Gaussian filter with σ = 0.005tff. (b) Instantaneous and integrated SFEs of the clouds, where ϵinst = M⋆/(Mgas + Msink + M⋆) and ϵint = M⋆/Mcloud = ϵ⋆. (c) Most massive star formed. (d) Number of formed stars. Dashed line: actual number of stars that would form from sampling the IMF given the amount of gas mass collected for star formation by sink particles. Solid line: number of stars followed in TORCH after the sampled stellar population below 4 M⊙ has been agglomerated. Dotted line: number of stars above 20 M⊙ on the grid that are generating feedback. The number of stars can drop due to SNe, mass loss, or exiting the grid. (e) 3D stellar velocity dispersion. (f) Half-mass radius of the entire star cluster. (g) Total mass (dotted line), mass of stars (dashed line) and gas (solid line) on the grid. (h) Virial parameter of stars (dashed line) and gas (solid line), where αv = 0.5 is the equilibrium value. (i) Fraction of mass bound for stars (dashed line) and gas (solid line). |
Appendix B: Stellar modifications
B.1. Low-mass star agglomeration
Upwards of 106 stars can be expected to form from a 106 M⊙ cloud with a peak number density of  . Even with the best modern N-body codes, evolving this many single stars and higher order stellar systems in such a dense stellar environment with a gravity bridge from each star to the gas in a separate code is immensely computationally taxing. To reduce the strain on the N-body portion of the calculations, we chose to agglomerate all stars under a given mass into gravitational super-star particles of equivalent mass to their sum. We refer to this mass cutoff as the agglomerate mass.
. Even with the best modern N-body codes, evolving this many single stars and higher order stellar systems in such a dense stellar environment with a gravity bridge from each star to the gas in a separate code is immensely computationally taxing. To reduce the strain on the N-body portion of the calculations, we chose to agglomerate all stars under a given mass into gravitational super-star particles of equivalent mass to their sum. We refer to this mass cutoff as the agglomerate mass.
When a sink progresses through the list of stellar masses it will form, stars with masses under Magg are put aside until the sum of their masses is above Magg. Then a star particle is formed with the summed mass. Figure B.1 shows the reduction in number of stars formed in a cloud for a given agglomerate mass. For our choice of 4 M⊙, we only had 10% of the stars undergoing gravitational interactions compared to the case with no agglomeration. This reduced our N-body execution time by a factor of somewhere between the 10log10 expected for the tree and 103 expected for the direct N portion of the PETAR algorithm. We note that the feedback from these low-mass stars is shown in Appendix B.2 to be negligible compared to that of the higher-mass stars, and in any case the current TORCH version does not model feedback from stars  as we neglect jets, while the ionizing radiation from such low-mass stars is negligible. In this study, we further limited feedback to only come from stars
as we neglect jets, while the ionizing radiation from such low-mass stars is negligible. In this study, we further limited feedback to only come from stars  as we discuss in the next subsection. The primary missing contribution from low-mass stars physically is their mutual gravitational interactions, which could potentially lead to the ejection of some fraction of them. However, the dynamics driven by those low-mass stars is also expected to be negligible in comparison to the effect of gas and more massive stars in the cluster. TORCH simulations with no mass agglomeration were done by Cournoyer-Cloutier et al. (2023), and in analyzing the morphology of clusters they find that the gravitational effects of the gas dominate over any stellar dynamics effect for the overall evolution of the cluster while it remains embedded.
as we discuss in the next subsection. The primary missing contribution from low-mass stars physically is their mutual gravitational interactions, which could potentially lead to the ejection of some fraction of them. However, the dynamics driven by those low-mass stars is also expected to be negligible in comparison to the effect of gas and more massive stars in the cluster. TORCH simulations with no mass agglomeration were done by Cournoyer-Cloutier et al. (2023), and in analyzing the morphology of clusters they find that the gravitational effects of the gas dominate over any stellar dynamics effect for the overall evolution of the cluster while it remains embedded.
B.2. Feedback mass limit
We limited all forms of stellar feedback—winds, radiation, and SNe—to stars above 20M⊙ instead of the value of 8M⊙ (lower bound for SN explosions) usually adopted in TORCH. This is necessary to significantly reduce the number of rays on the grid, which greatly decreases the calculation time and memory overhead for the ray-tracing algorithm. We quantify the effects of excluding radiation and winds from stars with masses below 20M⊙ by comparing the power output in the form of winds and radiation from all stars above 8M⊙ and above 20M⊙. We only allowed stars above 20 M⊙ to explode as SNe. Our simulations ran for  , which is roughly the main-sequence lifetime of a 20 M⊙ star. Stars under 20 M⊙ do not explode as SNe in the timeframe of our simulations, so excluding their SNe feedback makes no practical difference for this comparison.
, which is roughly the main-sequence lifetime of a 20 M⊙ star. Stars under 20 M⊙ do not explode as SNe in the timeframe of our simulations, so excluding their SNe feedback makes no practical difference for this comparison.
The power as a function of mass in the form of EUV radiation, non-ionizing FUV radiation, and stellar wind is shown in Figure B.2. We calculate these powers by taking stars from 8 to 100M⊙ in 1M⊙ increments, evolving them in SEBA for 1 Myr, and summing the energy output of each feedback channel. From this figure we can see that the power output of stellar winds and UV radiation is several orders of magnitude higher for stars above 20M⊙ than for stars closer to 8M⊙. Although stars in the 8–20 M⊙ mass range still output a considerable amount of FUV radiation, stars above 20 M⊙ account for over 80% of the total radiation power.
Although the feedback power is much stronger for stars above 20M⊙, stars with masses 8–20M⊙ greatly outnumber them. To find the ratio of feedback power for stars below and above 20 M⊙, we convolve the number of stars of each mass with the power output for each stellar mass (Fig. B.3). In the top left histogram, we show the ratio of stars with mass 8–20 M⊙ to stars with mass 20–100 M⊙ in all three simulations, sampled at their respective initial free-fall times. All three runs have more stars in the lower-mass bin. In the top right plot, we show the ratio of total stellar feedback power PFB (excluding SNe) for the stars in the two mass bins considered. We can see that although the lower-mass stars outnumber the higher-mass stars, the higher-mass stars still account for > 80% of the total stellar feedback energy. This shows that only including feedback from stars above 20 M⊙ still retains almost all of the feedback energy produced after the formation of all three star clusters.
The bottom panel in Figure B.3 shows the feedback power per mass bin for each separate feedback process. For the EUV radiation and wind feedback, the low-mass stars contribute practically nothing to the feedback energy in comparison to the high-mass stars. The FUV feedback of low-mass stars is not negligible, but is still well below 20% of the total FUV feedback energy from all stars.
B.3. Mass-loading stellar winds
In TORCH, the stellar wind feedback implementation is inspired by Simpson et al. (2015), using a method of momentum injection, the details of which can be found in Wall et al. (2020). The energy of the cells within the wind injection radius of the star is increased based on the mechanical luminosity of the wind Lw = (1/2)̇Mvw2, where ̇M is the stellar mass loss rate (Vink et al. 2000) and vw is the terminal wind velocity (Kudritzki & Puls 2000). The wind injection radius is set by comparing the cell width Δx to the wind termination shock radius (Weaver et al. 1977)
where ρ0 is the background density and tw is the age of the wind-blowing star at the given time step. If Rw < Δx the injection radius is set to Δx, otherwise it is set to a maximum value of  , at which we have found that spherical winds are well resolved. Momentum and energy are conserved when injecting stellar winds.
, at which we have found that spherical winds are well resolved. Momentum and energy are conserved when injecting stellar winds.
Within a stellar wind bubble, in dense clumpy regions of star formation such as the ones in our simulations, material will be swept up into the flow of the hot bubble by mass loading processes such as photoevaporation and hydrodynamic ablation (Dyson & Hartquist 1992; Hartquist & Dyson 1996; Pittard et al. 2001; Lancaster et al. 2021). With enough mass loading, the density increase will result in much more efficient cooling and create momentum-driven rather than energy-driven bubbles. The amount of mass-loading in the case of hydrodynamic ablation depends on the prevalence of dense clumps within the wind region as well as the Mach number M of the flow around the clump. With a supersonic flow, the mass-loading rate saturates. With a subsonic flow, the mass-loading rate is proportional to M4/3 (Smith et al. 1984; Hartquist et al. 1986). Accounting for mass loading in stellar wind models has been shown to successfully reproduce the kinematic properties of the observed stellar wind bubble of the Wolf-Rayet star RCW 58 (Arthur et al. 1993, 1996; Arthur 2007).
Simply injecting winds at vw does not account for these mass-loading processes and results in unphysically hot bubbles. Therefore, we chose a lower temperature target for our bubbles and lowered the wind velocity vw such that the final temperature of the wind bubble is the correct one. We conserved momentum and energy when injecting stellar winds, so while lowering the wind velocity, we also infused correspondingly more mass into the bubble than the stellar mass loss calculated. This mass is not taken off the grid elsewhere, meaning mass was not entirely conserved. At 1.25 tff, the total amount of mass that has been injected due to mass-loading as a fraction of initial cloud mass is 0.04, 0.02, and 0.01 for M4, M5, and M6.
Observed circumstellar bubbles cooled by suspected mass loading have been seen with temperatures as low as  in the S308 bubble (Chu et al. 2003). The spectra of the NGC 6888 bubble indicates a dominant component almost as cool, with
in the S308 bubble (Chu et al. 2003). The spectra of the NGC 6888 bubble indicates a dominant component almost as cool, with  (Bochkarev 1988; Wrigge et al. 1994; Wrigge 1999).
(Bochkarev 1988; Wrigge et al. 1994; Wrigge 1999).
In the simulations presented here, we heavily mass loaded the stellar winds to achieve a lower than observed bubble temperature of Tb = 3 × 105 K. This temperature is at the peak of the cooling curve, so the shocked wind rapidly cools, resulting in smaller, cooler, momentum-driven bubbles instead of hot bubbles filled with 106 K gas. We chose to do so because the high sound speeds in hot wind bubbles lower the Courant time step significantly, making the computation impractical. Since we do not follow X-rays through ray-tracing, having cooler bubbles is adequate. Bubbles at this temperature also do not affect the ionization of the surrounding gas. The primary action of wind feedback during cluster formation is to clear out dense regions of gas so that radiatively ionized H II regions can expand. The only hot gas (≥106 K) on the grid comes from SNe. Capping the temperature of gas on the grid at 3 × 105 K until SNe occur significantly speeds up the simulations.
 |
Fig. B.1. Fraction of the number of stars formed with agglomeration of stars below the mass on the x-axis over the total number of stars sampled by the IMF. We used |
 |
Fig. B.2. Power of stellar feedback in the form of winds and FUV and EUV radiation for different stellar masses. Left of the vertical line shows the amount of feedback power lost per star by excluding feedback from stars below 20 M⊙. |
 |
Fig. B.3. Power output of stellar feedback modes for each stellar mass regime. (Top left): Histogram showing the fractional stellar population of the three runs at one free-fall time, split into the mass regimes of 8–20 and 20–100 M⊙. (Top right): Fraction of feedback power in each mass regime. (Bottom): Histograms showing the fraction of feedback power for FUV, EUV, and winds in each mass regime. Although there are more lower-mass stars, the feedback produced by them is less than 20% of the total feedback energy for all stars. |
B.4. Effect on star formation efficiency
Limiting the temperature of stellar winds and only modelling feedback for stars above 20 M⊙ could potentially lead to un-physical runaway star formation. To test this, we re-ran the M6 model at early times to see if these two approximations are the cause for the extremely high SFE of 85%. For the first new M6 run we raised the wind temperature from  to
to  . For the second test, we both raised the wind temperature and modelled feedback for all stars above 8 M⊙. The SFE over time for the fiducial M6 run with our standard approximations and the new M6 models are shown in Figure B.4.
. For the second test, we both raised the wind temperature and modelled feedback for all stars above 8 M⊙. The SFE over time for the fiducial M6 run with our standard approximations and the new M6 models are shown in Figure B.4.
The two runs without the approximations that reduce the strength of the stellar feedback have similar SFEs as the M6 model with the aforementioned approximations. This validates our approximations and supports our argument that the high SFE in model M6 is not an artifact of under-estimating the strength of stellar feedback.
 |
Fig. B.4. Star formation efficiency over time for the fiducial M6 cloud with Tw = 300,000 K and |
All Tables
All Figures
 |
Fig. 1. Slice plots of the three simulations in the x–y plane over time. The plane of the slices for a given cloud is the center of stellar mass in the final snapshot. Stellar positions are shown by white dots. The free-fall times tff are given in Table 1. The number of stars shows the amount of star particles in the domain, not the number sampled from the IMF. Due to our agglomeration of low-mass star particles, the number of stars sampled from the IMF is ∼10× greater. |
| In the text | |
 |
Fig. 2. Still of the interactive plot of the embedded M4, M5, and M6 clusters (left to right) at 1 tff. The interactive plot file is available for download from the repository. |
| In the text | |
 |
Fig. 3. Wall-clock time for an evolution step for PETAR and PH4+MULTIPLES given the number of stars. |
| In the text | |
 |
Fig. 4. Global properties of the clusters and gas over time for models M4 (orange), M5 (maroon), and M6 (blue-violet) in units of free-fall time tff of the initial cloud (given in Table 1). From top left to bottom right: (a) SFR, where the transparent lines show the SFR at each star formation event, and the solid lines give the SFR smoothed using a Gaussian filter with σ = 0.005tff. (b) Instantaneous and integrated SFEs of the clouds, where ϵinst = M⋆/(Mgas + Msink + M⋆) and ϵint = M⋆/Mcloud = ϵ⋆. (c) Most massive star formed. (d) Number of formed stars. Dashed line: actual number of stars that would form from sampling the IMF given the amount of gas mass collected for star formation by sink particles. Solid line: number of stars followed in TORCH after the sampled stellar population below 4 M⊙ has been agglomerated. Dotted line: number of stars above 20 M⊙ on the grid that are generating feedback. The number of stars can drop due to SN, mass loss, or exiting the grid. (e) 3D stellar velocity dispersion. (f) Half-mass radius of the entire star cluster. (g) Total mass (dotted line), mass of stars (dashed line) and gas (solid line) on the grid. (h) Virial parameter of stars (dashed line) and gas (solid line), where αv = 0.5 is the equilibrium value. (i) Fraction of mass bound for stars (dashed line) and gas (solid line). |
| In the text | |
 |
Fig. 5. Size-line width coefficient versus surface density for the Firecracker cloud (Finn et al. 2019) and the M4, M5, and M6 clouds. The four red diamonds are observations, done using apertures (1–4) with radii R = 6.4, 15, 26, and 37 pc. The other points are our simulations, with connected points corresponding to apertures (1–4) of radii R = 5, 10, 15 and 20 pc. The colors indicate how much stellar mass has been produced (with empty points indicating no star formation). The lines correspond to virial equilibrium and free-fall as labeled (see Fig. 2 of Ballesteros-Paredes et al. 2011). |
| In the text | |
 |
Fig. 6. WARPFIELD evolution of shell radius versus time with different initial SFEs with the same parameters described in M6. In all cases, stellar feedback is inefficient in dispersing the surrounding dense cloud, and the shell eventually undergoes re-collapse. |
| In the text | |
 |
Fig. A.1. Global properties of the clusters and gas over time for models M4 (orange), M5 (maroon), and M6 (blue-violet) for comparison to Figure 4, where units of free-fall time (see Table 1) are used. From top left to bottom right: (a) SFR, where the transparent lines show the SFR at each star formation event, and the solid lines give the SFR smoothed using a Gaussian filter with σ = 0.005tff. (b) Instantaneous and integrated SFEs of the clouds, where ϵinst = M⋆/(Mgas + Msink + M⋆) and ϵint = M⋆/Mcloud = ϵ⋆. (c) Most massive star formed. (d) Number of formed stars. Dashed line: actual number of stars that would form from sampling the IMF given the amount of gas mass collected for star formation by sink particles. Solid line: number of stars followed in TORCH after the sampled stellar population below 4 M⊙ has been agglomerated. Dotted line: number of stars above 20 M⊙ on the grid that are generating feedback. The number of stars can drop due to SNe, mass loss, or exiting the grid. (e) 3D stellar velocity dispersion. (f) Half-mass radius of the entire star cluster. (g) Total mass (dotted line), mass of stars (dashed line) and gas (solid line) on the grid. (h) Virial parameter of stars (dashed line) and gas (solid line), where αv = 0.5 is the equilibrium value. (i) Fraction of mass bound for stars (dashed line) and gas (solid line). |
| In the text | |
 |
Fig. B.1. Fraction of the number of stars formed with agglomeration of stars below the mass on the x-axis over the total number of stars sampled by the IMF. We used |
| In the text | |
 |
Fig. B.2. Power of stellar feedback in the form of winds and FUV and EUV radiation for different stellar masses. Left of the vertical line shows the amount of feedback power lost per star by excluding feedback from stars below 20 M⊙. |
| In the text | |
 |
Fig. B.3. Power output of stellar feedback modes for each stellar mass regime. (Top left): Histogram showing the fractional stellar population of the three runs at one free-fall time, split into the mass regimes of 8–20 and 20–100 M⊙. (Top right): Fraction of feedback power in each mass regime. (Bottom): Histograms showing the fraction of feedback power for FUV, EUV, and winds in each mass regime. Although there are more lower-mass stars, the feedback produced by them is less than 20% of the total feedback energy for all stars. |
| In the text | |
 |
Fig. B.4. Star formation efficiency over time for the fiducial M6 cloud with Tw = 300,000 K and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





![$$ \begin{aligned} \Bigg [\frac{M}{\Phi }\Bigg ]_c=\frac{\zeta }{3\pi }\sqrt{\frac{5}{G}} = 490\ \frac{\mathrm{g}}{\mathrm{Gauss\,cm}^2}\;, \end{aligned} $$](/articles/aa/full_html/2024/10/aa48840-23/aa48840-23-eq13.gif)
![$$ \begin{aligned} B_z(x,{ y}) = B_0 \exp \left[ - (x^2+{ y}^2) \ln (3) / R_\mathrm{cl} ^2 \right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa48840-23/aa48840-23-eq15.gif)