EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A89 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A89
Number of page(s) 17
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202449579
Published online 01 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Dust stands out as one of the most intriguing baryonic components in galaxies. While it constitutes only ∼0.001 − 0.01% of the baryonic matter by mass, its emission contributes to about half of the electromagnetic content of our Universe that comes from galaxy formation and evolution processes (Dole et al. 2006). Dust is essential to the chemistry and physics of the interstellar medium (ISM), and, as has traditionally been recognised, its attenuation effects are significant in the ultraviolet (UV) and optical wavelengths (Cardelli et al. 1989; Gordon et al. 1997; Weingartner & Draine 2001; Calzetti et al. 2000; Salim & Narayanan 2020, among many more).

Among different components of interstellar dust, polycyclic aromatic hydrocarbons (PAHs) stand out, as not only are they abundant throughout the Universe, they influence the chemistry and thermal budget of the ISM by controlling the ionisation balance, dominating the heating process in neutral gas through photoelectric heating (Bakes & Tielens 1994; Wolfire et al. 1995; Helou et al. 2001), and acting as catalysts for the formation of H2 molecules (Thrower et al. 2012; Boschman et al. 2015; Barrera et al. 2023). The PAHs undergo transient heating by absorbing single UV photons and emit light in the mid-infrared (mid-IR) range from ∼3 − 20 μm, with the strongest emission at 7.7 μm. Their broad emission features are widely observed in the spectra of star-forming galaxies, contributing to up to 20% of the total IR emission (Lagache et al. 2004; Smith et al. 2007; Tielens 2008; Li 2020).

Polycyclic aromatic hydrocarbons have been studied extensively in the local Universe. Their mass or luminosity fraction relative to that of the total dust is observed to decrease below a certain gas-phase metallicity of 12 + log(O/H) ∼ 8.1 − 8.3, depending on different calibrations (Engelbracht et al. 2005; Madden et al. 2006; Draine et al. 2007; Marble et al. 2010; Rémy-Ruyer et al. 2015; Aniano et al. 2020). The underlying physical cause of this behaviour is generally attributed to either a lack of production or preferential destruction at low metallicities. The reduced PAH abundance at low metallicities may be due to a lower abundance of carbon in the gas phase preventing PAH formation in the ISM (Draine et al. 2007) or a deficiency of stars that produce PAHs (such as AGB stars; Galliano et al. 2008). It may also be due to a rapid destruction of PAHs by the more intense and harder UV radiation in the low-metallicity ISM systems in which dust shielding is reduced (Madden et al. 2006; Hunt et al. 2010; Xie & Ho 2019) or by thermal sputtering in shock-heated gas with a lower cooling rate because of low metallicity (Li 2020). The increased abundance of PAHs at higher metallicities is also attributed to an accelerated production path through shattering, which becomes more efficient above a certain metallicity (Seok et al. 2014).

Owing to its prevalence and being accessible by various IR telescopes, the ∼7 − 8 μm mid-IR emission is calibrated as a practical and useful indicator of obscured luminosity and the star formation rate (SFR) in the metal-rich star-forming galaxies regime (Peeters et al. 2004; Calzetti et al. 2007; Kennicutt et al. 2009; Rujopakarn et al. 2013; Shipley et al. 2016). This calibration is often combined with unobscured tracers, such as UV and optical emission lines, to provide a total SFR estimation (Kennicutt & Evans 2012). At z ∼ 1 − 3, known as cosmic noon, the 7.7 μm PAH emission was captured by Spitzer/MIPS 24 μm (Rieke et al. 2004), making it a widely used tracer of obscured luminosity and SFR to advance our knowledge about SFR evolution and the star-forming main sequence (Reddy et al. 2008; Elbaz et al. 2011; Rujopakarn et al. 2013; Whitaker et al. 2012; Shivaei et al. 2015, 2017), obscured fraction (Reddy et al. 2010; Whitaker et al. 2017), and IR luminosity function (Pérez-González et al. 2005; Le Floc’h et al. 2005; Magnelli et al. 2011), as well as to study PAH characteristics themselves (Shivaei et al. 2017). However, MIPS confusion noise (Dole et al. 2004) inevitably constrained these studies to more IR-bright, dusty, and massive galaxies at cosmic noon. While some studies employ sophisticated stacking techniques to extend the dynamic range to lower-mass galaxies, this approach by definition sacrifices information about the properties of individual galaxies.

The perspective on mid-IR dust emission in galaxies beyond the local Universe has undergone a significant shift with the advent of the Mid-Infrared Instrument (MIRI; Rieke et al. 2015; Wright et al. 2023) on the James Webb Space Telescope (JWST; Gardner et al. 2023). This instrument offers an order-of-magnitude improvement in spatial resolution without the confusion noise limitation at comparable wavelengths to MIPS. Moreover, its continuous wavelength coverage from 5 to 25 μm with nine intermediate-width photometric bands provides a leap forward in characterising sources compared to its predecessors. This allows for novel studies of dust, both in the local Universe (Álvarez-Márquez et al. 2023; Sandstrom et al. 2023; Chastenet et al. 2023; Armus et al. 2023) and beyond (Kirkpatrick et al. 2023; Lyu et al. 2024; Lin et al. 2024; Pérez-González et al. 2024). Importantly, the high angular resolution enables not only the detection of dust emission from individual typical galaxies at z > 0.5, but also, in many cases, the measurement of the spatial extent and morphology of the dust within the galaxies (Shen et al. 2023; Magnelli et al. 2023) – providing new opportunities to explore the dust content of galaxies all the way to cosmic noon.

Here, we present the first paper of the Systematic Mid-infrared Instrument Legacy Extragalactic Survey (SMILES; GTO 1207) on the PAH and dust emission of star-forming galaxies at z = 0.7 − 2.0. SMILES is the widest MIRI survey in Cycles 1 and 2 of JWST observations and covers the full MIRI photometric range from 5.6 to 25.5 μm. The comprehensive multi-wavelength coverage facilitates a robust investigation of PAHs and dust emission in one of the richest extragalactic deep fields, the Great Observatories Origins Deep Survey South (GOODS-S; Dickinson et al. 2003). The structure of the paper is as follows. In Section 2, we detail the dataset used and the methodologies employed to estimate various physical properties of galaxies, including the spectral energy distribution (SED) fitting. Section 3 presents the results on the evolution of PAH mass and luminosity fraction from z ∼ 0 to 2. In Section 4, we investigate the obscured UV luminosity fraction of galaxies as a function of mass and SFR surface density. The findings are summarised in Section 5. Throughout this paper, we assume a ΛCDM flat cosmology with H0 = 70 km s−1 Mpc−1 and ΩΛ = 0.7, and a Chabrier (2003) initial mass function (IMF).

2. Methods and observations

2.1. SMILES survey (MIRI data)

This paper is based on the MIRI imaging survey of Systematic Mid-infrared Instrument Legacy Extragalactic Survey (SMILES; Rieke et al. 2024; Alberts et al. 2024). SMILES is a MIRI US-GTO programme (PID 1207, PI: George Rieke) that surveys 34 arcmin2 (using 15 MIRI pointings in a 3 × 5 mosaic) centred on the Hubble Ultra Deep Field (HUDF; Beckwith et al. 2006). The survey is centred at 03h32m34.80s −27d48m32.60s and includes the eight broad bands of the MIRI Imager from 5.6 to 25.5 μm. A standard MIRI 4-point dither pattern was adopted to improve the point spread function (PSF) sampling and mitigate detector artifacts and cosmic-ray events. We used a FASTR1 readout pattern. Each pointing had a total science exposure time of 2.17 hours, divided over eight bands. The exposure times per band were designed to optimise the detection of typical active galactic nucleus (AGN) and star-forming galaxies down to an SFR of ∼10 M⊙ yr−1. The observations were carried out in December 2022 and January 2023, which achieved a 5σ point source sensitivity of 0.11 μJy (AB mag = 26.3), 0.20 μJy (25.6), 0.48 (24.7), 0.67 (24.3), 0.79 (24.2), 2.42 (22.9), 3.47 (22.6), and 16.91 (20.8) in F560W (754 s exposure time), F770W (866 s), F1000W (644 s), F1280W (755 s), F1500W (1121 s), F1800W (755 s), F2100W (2186 s), and F2550W (832 s)1. The achieved sensitivities are an order of magnitude deeper than the confusion limit of Spitzer/MIPS 24 μm (56 μJy; Dole et al. 2004) at similar wavelengths. The optimal combination of depth, spatial resolution, coverage area, and multi-wavelength capabilities makes SMILES well suited to investigating mid-IR dust emissions in galaxies during the cosmic noon epoch. In Figure 1, we show the advancement of this dataset compared to the existing IR data to study cosmic noon galaxies.

thumbnail Fig. 1.

Power of SMILES in studying the mid-IR dust properties of galaxies at cosmic noon. Left: The top-left image shows a group of galaxies at z ∼ 0.7 − 2.3 (matching the redshift range in this paper) in F444W/F200W/F090W NIRCam colours (JADES). The pre-JWST mid-IR view of these galaxies is shown in the top row from Spitzer IRAC and MIPS (GOODS survey; Dickinson & FIDEL Team 2007; Ashby et al. 2015). The bottom two rows show the mid-IR images with JWST MIRI at 5.6, 7.7, 10, 12.8, 15, 18, 21, and 25.5 μm (SMILES). The PSF sizes are shown with white circles in the corners (diameter of the circle is the FWHM). The unprecedented improvement of MIRI in spatial resolution (0.19 to 0.86″ from 5.6 to 25.5 μm) compared to that of IRAC (1.72 and 1.88″ at 5.8 and 8 μm) and MIPS 24 μm (6″) makes it possible to observe the mid-IR emission of individual typical galaxies at these redshifts. Right: The IR dust SEDs of typical galaxies at z = 1.8 with IR luminosities of 1010.5 − 1011.5 L⊙ (Rieke et al. 2009; corresponding to obscured SFRs of ∼5 − 50 M⊙/yr assuming the Kennicutt & Evans 2012 calibration) in grey shaded region, along with 3σ sensitivity limits of the GOODS-S Herschel/PACS (green; Magnelli et al. 2013), Spitzer/MIPS 24 μm confusion limit (red; 56 μJy, Dole et al. 2004), Spitzer IRAC Channels 3 and 4 (blue; Guo et al. 2013), and the MIRI sensitivities of SMILES in ∼10 − 30 min exposures (orange; Section 2.1). MIRI filter transmission curves are shown with orange shaded regions. The high sensitivity and multi-band capability of MIRI enables measurements and characterisations of IR emission of typical galaxies at cosmic noon.

Data reduction. Data reduction of MIRI images was performed using the nominal JWST Pipeline released by the Space Telescope Science Institute (JWST Calibration Pipeline v1.10.0; Bushouse et al. 2023), using JWST Calibration Reference System (CRDS) jwst 1084.pmap, with two custom modifications on the background subtraction and astrometry, and a post-processing flux calibration correction on F560W and F770W (see below). After the astrometric and background corrections, the final MIRI mosaic was made through the Pipeline stage 3 with a pixel scale of 0.06″.

Background correction. MIRI photometry relies on background-limited sensitivity across all bands, but particularly at longer wavelengths at which the thermal emission from the telescope is significant (Glasse et al. 2015; Rigby et al. 2023). The background imprints a large spatial gradient on the image (Dicken et al. 2024). In addition, in some cases there are tree-ring-shaped features and striping along the detector columns and rows (Morrison et al. 2023) that can also be corrected for during the background subtraction step. Therefore, proper correction is crucial to reach maximum sensitivity. We adopted a custom background subtraction methodology that is explained in detail in Pérez-González et al. (2024) and Alberts et al. (2024). In brief, this routine was performed on the products of the CALWEBB IMAGE2 (cal files) step of the pipeline. It combines the cal images taken in the same band from different pointings to create a ‘super-background’, departing from the routine in the JWST pipeline, which utilises only the four dithers for each pointing. Through an iterative process, for each cal file, we masked out sources, large gradients, and striping using median filtering. This way, the super-background was constructed for each uncleaned cal file. Finally, a median subtraction was applied to remove any remaining background variation, usually caused by cosmic ray showers.

Astrometry correction. This step was done on the background-subtracted cal files, the output from the previous paragraph. The tweakreg step in the Pipeline (in stage 3) was designed to calculate the astrometry correction of the image. However, in the earlier versions it was designed for automated processing without a user input reference catalogue. As the MIRI images do not cover an area of the sky large enough to contain a sufficient number of Gaia point sources, it is necessary to supply an external reference catalogue made from the Hubble Space Telescope (HST), or NIRCam images in the field were necessary. We adopted the tweakwcs package with a custom routine outside of the Pipeline. We used the NIRCam F444W mosaic (JADES survey; registered to Gaia DR3) to correct the F560W image by creating matched catalogues of high signal-to-noise (S/N) F444W and F560W sources. We used the registered F560W to correct F770W, and so on, up to F1500W. The F1500W was used to correct F1800W, F2100W, and F2550W images as the number of high S/N sources in each band was insufficient for independent corrections. The achieved astrometric accuracy is 0.01 − 0.02″ (1σ) in all filters except for F2550W, which has a low number of high S/N sources and an astrometric accuracy of ∼0.04″.

Flux calibration correction. After data reduction and photometry (see below), we realised the F560W and F770W flux measurements are systematically overestimated. This became apparent when the predicted F560W fluxes from full SED fitting to HST, NIRCam, and MIRI data (excluding F560W) of sources with spectroscopic redshifts were consistently lower than the observed F560W photometry. Moreover, we compared the photometry with Spitzer IRAC and found a similar systematic overestimation in MIRI photometry. Based on simulations of the PSF, we concluded that this is likely due to an underestimation of the cruciform spikes of the MIRI PSF (Gáspár et al. 2021) in the flux calibration step of the Pipeline (this is now updated in the Pipeline; see below). Therefore, we calculated correction factors by comparing the observed F560W and F770W fluxes with the predicted fluxes from best-fit SEDs of 25 isolated stars using ASTRODEEP photometry up to IRAC2 (Lyu et al. 2024). The correction factors of 1.26 and 1.04 were applied to the F560W and F770W Kron fluxes, respectively (see below for photometry). The absolute flux calibration was updated in the JWST Calibration Reference Data System (CRDS) after the current reductions on December 14, 2023, to better account for the cruciform effect and the time dependence of MIRI sensitivity (Gordon et al., in prep.). The correction factors relevant to SMILES are 1.27 and 1.18 in F560W and F770W, respectively. While the F560W correction is in agreement with our calculations, the official new calibrations for F770W are higher than ours. However, since the presented work is not highly dependent on the F770W flux (rest-frame of ∼2.5 − 4.5 μm), our results will be unchanged with either correction factor.

Photometry. MIRI source detection and photometric extraction were performed using a modified version of the JADES photometric pipeline (jades-pipeline, for the pipeline see Rieke et al. 2023; Robertson et al. 2024; for MIRI photometry see also Lyu et al. 2024). We briefly summarise the main points here: a detection and S/N map were constructed by stacking the F560W and F770W mosaics, which were then used to define an initial blended segmentation map down to a low threshold in source S/N. This segmentation map was then processed to optimally deblend sources and remove spurious noise spikes. The final segmentation map and detection image were then used to define source centroids and photometry was measured in all filters at these centroids. In this work, we adopted 2.5× scaled Kron photometry. As was noted above, correction factors were applied to the flux calibration at F560W and F770W. Aperture corrections were determined as the fraction of flux outside a given Kron aperture based on empirical PSFs for F560W and F770W (using comissioning data PID 1028, Dicken et al. 2024; A. Gáspar, priv. comm.) and model PSFs generated from WebbPSF (Perrin et al. 2014) for the other bands. Photometric uncertainties were derived by placing apertures at random positions on a masked mosaic, which accounts for correlated pixel noise. A more detailed description of the construction of the SMILES photometric catalogue is presented in Alberts et al. (2024).

2.1.1. JADES, JEMS, and HST data

We used deep NIRCam imaging data in multiple filters spanning 1−5 μm from the JWST Advanced Deep Extragalactic Survey (JADES) in GOODS-S (PID 1180, PI: D. Eisenstein) and the medium bands of the JWST Extragalactic Medium-band Survey (JEMS, PID 1963, Williams et al. 2023). We refer to the JADES survey data release papers for further details on the observations and data reduction (Rieke et al. 2023; Eisenstein et al. 2023). In brief, JADES GOODS-S covers a total of 67 square-arcminutes. The survey has two tiers: (i) Deep with 27 square-arcminutes in NIRCam F090W, F115W, F150W, F200W, F277W, F335M, F356W, F410M, and F444W bands, and (ii) Medium with 40 square-arcminutes with the same filters, but without F335M. We also included NIRCam medium bands F210M, F430M, F460M, and F480M from the JEMS survey, where available.

We used Kron photometry from the custom-developed jades-pipeline (discussed in Section 2.1; Robertson et al. 2024; Rieke et al. 2023). Furthermore, we used the spectroscopic redshifts from JADES NIRSpec (Bunker et al. 2024), where available (Section 2.3.3). To cover the shorter wavelengths, we also included existing HST/ACS F435W, F606W, F775W, F814W, and F850LP data from the Hubble Legacy Fields (HLF) v2.0 (Illingworth et al. 2013), applying the same photometry jades-pipeline as for the NIRCam data.

2.1.2. FRESCO data and redshifts

The field of SMILES is fully covered by the FRESCO-GOODS-S F444W grism survey (PID 1895, Oesch et al. 2023), which results in the detection of Paα at z ∼ 1.0 − 1.7 and Paβ at z ∼ 2.0 − 2.9.

The details of the grism data reduction and extractions are in Oesch et al. (2023). We extracted the grism spectra for 1296 MIRI-selected galaxies (3σ detected in F560W or F770W) at z = 0.5 − 3.5 based on existing spectroscopic redshifts from the literature and photometric redshifts based on HST/ACS+JADES/NIRCam. The extractions follow the standard continuum+contamination removal procedure explained in Oesch et al. (2023) and Kashino et al. (2023). The spectra were fit within Δ(z) =  ± 0.02(1 + zspec) for the objects with existing spec-z; otherwise, within the lower and upper 68% quantiles of their photo-z. The redshift probability distributions were then calculated mainly based on the detections of Paα at z = 1.07 − 1.66, Paβ at z = 2.03 − 2.88, and/or HeIλ1083, [SIII], [SII], and higher-order Paschen lines. We visually inspected all (N = 1296 objects) of the 1D extractions, the line fits, and accordingly evaluated the quality of the redshift estimations. The final sample statistics are: 30% (N = 386) have robust fits and redshifts, out of which 56% had prior spectroscopic redshifts; 50% (N = 653) of the fits are unreliable (e.g. no line, incomplete spectral coverage, contamination from other sources, etc.); and 20% (N = 257) are flagged as undetermined quality (noisy spectra, a weak line, or multiple lines that give different solutions). In total, 57% of galaxies in the MIRI-selected sample (N = 743 galaxies) have either a FRESCO redshift or another spectroscopic redshift (3DHST and other literature).

2.2. Final sample

We started from the MIRI-selected sample (3σ detected in F560W or F770W) and used the following criteria to define our final sample:

  1. z = 0.7 − 2.0 to ensure adequate PAH coverage by MIRI data.

  2. 3σ detection in at least one MIRI band longwards of 15 μm.

  3. The removal of quiescent galaxies based on their rest-frame U − V and V − J colours (following Equation (3) in Schreiber et al. 2015). For a cleaner selection, we also removed galaxies with specific SFR (sSFR, SFR/M* from SED modelling, see Section 2.3) < 10−10 yr−1.

  4. The removal of objects with unusual or incorrect photometry from visual inspections of the SED fits.

This selection results in 443 galaxies (‘full’ sample). The stellar mass and SFR distribution is shown in Figure 2. Specifically for the PAH analysis in this work, we further limited the sample to those with ‘robust’ PAH mass fraction (qPAH, see Section 2.3.1). This category is defined as galaxies with either > 3σqPAH values or qPAH error of less than 0.5%. The second condition allows the inclusion of near-zero PAH fractions that are still relatively robust. The rest of the sample is denoted as ‘low confidence’ qPAH throughout the paper. The robust qPAH sample has 216 objects. Figure 3 shows the distributions of redshift, F444W (tracing emission from old stellar populations), and F1500W (tracing PAH and dust emission) of the robust and full samples. The robust qPAH sample is skewed towards brighter galaxies (and relatively more massive and dusty), by definition. Even though this sub-sample is biased, the separation is necessary to have a sample with reliable PAH fraction estimates. However, we show the results and trends for the low-confidence sample as well as the robust sample in the paper. The properties of the robust qPAH sample are provided in an online repository2 and a sample table is shown in Table 1.

thumbnail Fig. 2.

Left panel: SFR versus stellar mass of the sample. The sample is divided into those with robust and low-confidence PAH mass fractions (same as in Figure 3). The shaded region indicates star-forming main sequence at the redshift range of our galaxies, z = 0.7 − 2.0, derived from the PROSPECTOR-inferred SFR and mass of Leja et al. (2022), same as the SFR and stellar masses inferred in this work. Three SED examples of the symbols with red edges are shown on the right. Right panel: Examples of the SEDs of three galaxies that are above, on, and below the main sequence, shown with the red edges in the left plot. The MIRI filter transmission curves are also shown. The wealth of data from HST, NIRCam, and MIRI provides robust SED fits for this sample at z = 0.7 to 2.0. More examples of the SED fits are provided in the online repository: https://zenodo.org/records/12671075.

thumbnail Fig. 3.

Distributions of redshift (left), F444W flux density (middle), and F1500W flux density (right) for the full sample (N = 443) and the sub-sample with robust PAH mass fractions (N = 216) defined as those with qPAH error < 0.5% or qPAH parameter constrained by > 3σ from the SED fitting (Section 2.2). The sample is purely star-forming with AGN and quiescent galaxies removed (Section 2.2).

Table 1.

Properties of the robust qPAH sample (Section 2.2). Table contains: source ID from SMILES internal v0.3 catalog, redshift, PAH fraction and error, stellar mass and error in M⊙, metallicity (12 + log(O/H)) and error calculated from the fundamental metallicity relation (FMR; as plotted in Figures 8 and 9) and from the mass metallicity relation (MZR; as plotted in Figure 7).

2.3. Spectral energy distribution fitting

We adopted the PROSPECTOR SED fitting code (Johnson et al. 2021) to fit the UV to mid-IR photometry. PROSPECTOR is a highly flexible SED fitting code that is based on Bayesian forward modelling and Monte Carlo sampling of the parameter space using FSPS stellar populations (Conroy 2013). We have adopted the ‘current’ or ‘surviving’ stellar mass throughout this paper, which takes into account losses throughout the evolution of stars in the galaxy via AGB winds, supernovae, etc. This is different from the mass of stars that are formed in the lifetime of the galaxy. In our sample, the ratio of the surviving to the formed stellar mass is on average 0.69 with a scatter of 0.04 (for a Chabrier IMF). Below, we first discuss the assumptions on modelling the dust emission (Section 2.3.1), then discuss the validity of the derived PAH fractions (Section 2.3.2). Finally, in Section 2.3.3, we discuss the remaining assumptions in the SED fitting. We note that the main results of this paper (i.e. PAH and dust emission) are mainly constrained by the assumed dust models (Draine & Li 2007), and therefore using a different SED fitting code is not expected to significantly change the results.

2.3.1. Dust emission assumptions

The dust emission models in PROSPECTOR are based on the models of Draine & Li (2007). These models assume a mixture of amorphous silicate grains and carbonaceous grains with a distribution of grain sizes chosen to reproduce the wavelength dependence of the Milky Way (MW) extinction curve, while the silicate and carbonaceous content was constrained by the ISM gas phase depletion observations. The radiation field heating the dust is assumed to have a fixed shape (spectrum) of the local interstellar radiation field (Mathis et al. 1983), scaled by a dimensionless factor, U. Three parameters of these models are free in the PROSPECTOR framework: qPAH, the fraction of the grain mass contributed by PAHs containing fewer than 103 carbon atoms, Umin, the intensity of the diffuse ISM radiation field heating the dust, and γ, the fraction of dust mass exposed to the power-law distribution of starlight radiation intensities between Umin and Umax ((1 − γ) is the fraction of dust mass exposed to Umin).

In the absence of far-IR constraints, the IR parameters are constrained based on the energy balance assumption between the UV-near-IR dust attenuated luminosity and the re-emitted IR luminosity. Leja et al. (2017) experimented with the output with and without far-IR data on a large sample of local galaxies. They concluded that in the absence of far-IR constraints, it is critical to have tight priors on the shape of the far-IR emission to avoid unrealistically large uncertainties and potential systematic biases in SFR, LIR, and dust attenuation. Following their recommendation, we adopted a flat prior of 0.1 < Umin < 15 and 0.0 < γ < 0.15. For the qPAH parameter we adopted a flat prior of 0.4 < qPAH < 4.6, as this is the range of qPAH that the Draine & Li (2007) models are specifically constrained for. We derived qPAH for a sub-sample of the galaxies with ALMA 1.1 and 3 mm observations and find no systematic offset between the derived values including and excluding the ALMA data, as is explained in Section 2.3.2.

We note that the fraction of dust mass in PAHs used in this work, denoted as qPAH, should be distinguished from the fraction of total IR luminosity in PAH bands. The two quantities are related to each other but not with a constant value, as the light-to-mass ratio of dust is not a fixed value in the Draine & Li (2007) models (it is a function of radiation field intensity for the dust that produces the IR continuum and for PAHs, it depends on the stochastic heating). In Figure 4, we compare the two quantities for our sample. The PAH mass fraction is compared to the PAH luminosity fraction defined as either a ratio of PAH 7.7 μm feature (F7.7, left panel) or a total PAH luminosity (right panel) to total IR luminosity (integrated luminosity from 3 to 1100 μm). F7.7 is calculated as the integrated PAH flux ( ∫ ( F λ − F λ continuum ) d λ $ \int(F_{\lambda}-F^{\mathrm{continuum}}_{\lambda})\,\mathrm{d}\lambda $) between 6.9 and 9.7 μm and is corrected for the continuum emission by assuming zero feature strength on either side of the feature at 6.9 and 9.7 μm, following the recipe of Draine et al. (2021). The total PAH luminosity is the sum of the luminosity of the 3.3, 6.2, 7.7, 11.2, and 17 μm features, measured in the same way as the 7.7 μm luminosity within the windows defined by Draine et al. (2021). As is shown in the figure, the PAH mass fraction can be converted to the total PAH luminosity fraction by a factor of 0.68 (the median value of qPAH to total PAH luminosity fraction); however, there is a large scatter around this median value. The qPAH to PAH 7.7 μm luminosity fraction is tighter, but the relation with qPAH is not linear. We fitted the relationship with a polynomial function:

thumbnail Fig. 4.

Ratio of the PAH-to-dust mass fraction to the PAH-to-total IR luminosity fraction versus the PAH mass fraction in our sample. Both quantities are derived from the Draine & Li (2007) models (Section 2.3). Robust qPAH sample shows galaxies with qPAH with > 3σ significance or less than 0.5% error (Section 2.2). Left: PAH luminosity fraction is defined as the ratio of the PAH 7.7 μm feature luminosity to total IR luminosity. Horizontal line is the unity line. The robust sample is fit with a polynomial function shown with a dashed curve (Equation (1)). Right: PAH luminosity is the sum of the 3.3, 6.2, 7.7, 11.2, and 17 μm PAH features luminosities (Section 2.3.1). Horizontal line shows the median of the robust sample (0.68). We note that qPAH is not in percentage units, unlike the other figures in this paper.

q PAH F 7.7 / F TIR = − 0.024 × q PAH 2 + 0.158 × q PAH + 0.805 , $$ \begin{aligned} \frac{{q_{\rm PAH}}}{F_{7.7}/F_{\rm TIR}} = -0.024 \times {q_{\rm PAH}}^2 + 0.158\times {q_{\rm PAH}} + 0.805, \end{aligned} $$(1)

where F7.7/FTIR is the PAH 7.7 μm to total IR luminosity fraction, and qPAH is the fraction of PAH to dust mass. The qPAH values presented in this work can be converted to the PAH 7.7 μm luminosity fraction using this equation, if needed.

2.3.2. Robustness of qPAH inferred from photometry

The majority of our sample does not have IR detections beyond MIRI. Therefore, the PAH mass fractions were inferred solely based on UV to mid-IR (MIRI) data. As a validity check for the derived qPAH parameters, we performed two tests, as follows.

We compare the qPAH values for a sample of 18 galaxies at z = 0.7 − 0.9 that have significant (> 3σ) detections at 15 and 25.5 μm. As is shown in the right panel of Figure 5, z = 0.9 is the highest redshift that our longest-wavelength band (F2550W) traces the part of the SED that is dominated by the continuum dust emission, and not that of PAHs. At z = 0.7 − 0.9, the F1500W filter traces the 7 − 8 μm PAH complex. Therefore, the ratio of F1500W to F2550W fluxes traces the PAH to warm dust emission, which, in theory, is expected to scale with the PAH-to-dust mass fraction (i.e. qPAH). As is shown in the left panel of Figure 5, the derived qPAH values from the SED fits are highly correlated with the F1500W to F2550W flux ratio, with a Pearson correlation coefficient of 0.71 (p-value ≪ 1).

thumbnail Fig. 5.

Left panel: PAH-to-dust mass fraction (qPAH) versus 15 μm (F1500W) to 25.5 μm (F2550W) flux ratios for a sample of z = 0.7 − 0.9 galaxies with significant (> 3σ) detections in F1500W and F2550W. qPAH is derived from PROSPECTOR (the Draine & Li 2007 models), while the flux ratio is an empirical tracer of PAH to warm dust emission, as is shown in the right panel. The significant linear correlation of the two quantities (Pearson correlation coefficient of 0.71 with p-value = 0.001) indicates the validity of the estimated qPAH values. Right panel: Two mid-IR spectra with a high PAH fraction (solid) and low PAH fraction (dashed), overlaid with the wavelength coverage of the F1500W and F2550W filters at z = 0.7 − 0.9. In this redshift range, F1500W and F2550W filters trace the PAH dominated and non-PAH-dominated dust emission in star-forming galaxies, respectively. Therefore, their ratio is expected to correlate with PAH fraction.

As qPAH depends on both the PAH mass and the mass of the other dust grains, the parameter may be uncertain in the absence of far-IR data. There are 38 SMILES galaxies with ALMA 1.1 mm (band 6) detection from one of the deepest ALMA extragalactic surveys, ASPECS (Walter et al. 2016). Five of these also have 3 mm detections (band 3). We compare the derived qPAH of this sample including and excluding ALMA data in Figure 6. There is no systematic difference in qPAH within the uncertainties. Given the luminosity range of these galaxies, this is in agreement with previous studies that showed PAHs as good tracers of IR luminosity in relatively bright (and non-ULIRG) galaxies (Reddy et al. 2012; Shipley et al. 2016). Therefore, we conclude that our derived qPAH values are robust even without far-IR data under our fitting assumptions.

thumbnail Fig. 6.

PAH to total dust mass fraction for the 38 galaxies with ALMA 1.1 mm detection (from the ASPECS survey; Walter et al. 2016). Five of them also have 3 mm detections. The axes show the derived qPAH including and excluding the ALMA data points. Median of the qPAH values without ALMA to those with ALMA data is 0.95, completely within the qPAH uncertainty, indicating the qPAH values inferred based on UV-to-MIRI data alone are robust.

2.3.3. Other spectral energy distribution assumptions

We assumed a delayed-τ star formation history with a flat age prior between 1 Myr to the age of the Universe at the redshift of the galaxy. Stellar metallicity is free with a flat prior between log(Z/Z⊙) =  − 2.5 − 0.19. For dust attenuation, we adopted a flexible attenuation curve that has its UV slope as a free parameter as parameterised in Kriek & Conroy (2013), with a flat prior between −0.6 to 0.3 for the multiplicative coefficient of the slope of the Calzetti et al. (2000) curve. We included AGN emission, even though the AGN fraction of our sample is very low, by the definition of the sample (median of 0.05% AGN-to-bolometric stellar luminosity fraction). We assumed a nebular emission model with flat priors in logarithmic space of gas-phase metallicity at −2.0 to 0.5 (relative to solar metallicity) and ionisation parameter at −4 to −1. We included IGM absorption (Madau 1995) with the optical depth scaling factor as a free parameter with a Gaussian prior centred at 1.0 and σ = 0.3.

Redshift was fixed if the spectroscopic redshift was available from various non-JWST spectroscopic campaigns (compilations of Kodra et al. 2023; Bacon et al. 2023) or JWST JADES NIRSpec (Bunker et al. 2024) and FRESCO NIRCam grism (Oesch et al. 2023) surveys. In the absence of spec-z, the redshift parameter was left free with a a clipped-normal prior distribution centred at the photometric redshift and limits of the photo-z uncertainty. The photo-z was taken from the JADES photometric redshift catalogue (Hainline et al. 2023), with typical uncertainties of Δ(z)/z = 0.04 − 0.1 (median of 0.06).

2.4. MIRI sizes

Dust sizes and surface areas were estimated from MIRI data as a proxy for where the bulk of stars are forming in galaxies. These measurements were later used to calculate SFR surface densities. We calculated dust sizes from MIRI F1500W images with 0.5″ resolution, tracing rest-frame 5 − 9 μm. The choice of the F1500W filter to measure dust sizes was made as this filter provides a good compromise between wavelength and spatial resolution.

We used WebbPSF (Perrin et al. 2014) to model the F1500W PSF. In order to estimate sizes, we used GALFIT (Peng et al. 2002, 2010) to fit the spatial profile of each source. Each one was modelled twice: once with a point-source model and once with a single-Sersic model. For a complete morphological analysis, more complicated models are required but for our current purposes these simple models provide reasonable sizes for the majority of the sample. Galaxies that fit better (smaller reduced χ2) with a Sérsic model than the point-source model are considered spatially resolved. Sources that are best fit with the point source model or with a Sérsic profile but whose half-light radius is smaller than the 50% encircled energy radius for the appropriate filter are considered unresolved. For the unresolved sources, we used the 50% encircled energy size of the PSF as an upper limit on their effective radius. We visually inspected all fits and removed the bad fits (e.g. if the source had signs of merger or nearby bright companions). This results in 105 F1500W good fits for extended objects in our sample.

3. Evolution of the polycyclic aromatic hydrocarbon fraction

Figure 2 shows the full and the robust (qPAH determined at > 3σ) samples in the SFR–M* (star-forming main-sequence) diagram. The colours indicate the inferred qPAH for the robust sample, which ranges from ∼0.5 − 4.5%. The galaxies are representative of ‘main sequence’ galaxies at these redshifts (Leja et al. 2022) and span a wide range in sSFR. Examples of the SED fits for three objects that are above, on, and below the main-sequence are shown in the right panels. In the following sections, we investigate the relationship between PAH fractions and galaxy parameters, and its evolution from z ∼ 2 to z ∼ 0.

3.1. Polycyclic aromatic hydrocarbon fraction versus stellar mass

In Figure 7, we show the relationship between stellar mass and qPAH (left panel) and the 7.7 μm PAH luminosity fraction relative to total IR luminosity emission (F7.7/FTIR; right panel). F7.7 is the integrated PAH flux (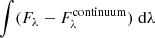 ∫ ( F λ − F λ continuum ) d λ $ \int(F_{\lambda}-F^{\mathrm{continuum}}_{\lambda})\;\mathrm{d}\lambda $) between 6.9 and 9.7 μm and is corrected for the continuum emission, following the recipe of Draine et al. (2021), and the total IR (TIR) power is the integrated emission (∫Fλ dλ) from 3 to 1100 μm of the best-fit SED model.

thumbnail Fig. 7.

PAH mass fraction (left) and luminosity fraction (right) as a function of stellar mass. Moving median (black curve) is shown for the robust qPAH sample (see Section 2.2 for the definition of samples), and all galaxies are colour-coded by sSFR. In the left panel, horizontal lines show the median PAH mass fractions of z ∼ 0 galaxies with 12 + log(O/H) < 8.1 and > 8.1 from Draine et al. (2007). On the top x-axes, we also show the estimated metallicities from the O3N2-based mass-metallicity relation (MZR) of Topping et al. (2021) at z ∼ 1.5, and assuming the Pettini & Pagel (2004) calibration. The z ∼ 0.7 − 2 sample has a very similar qPAH-metallicity behaviour to that inferred at z ∼ 0. Properties of the robust sample are in Table 1.

The PAH ‘strength’, defined as either the PAH mass or emission fraction, is positively correlated with stellar mass with a correlation coefficient of ρPearson = 0.5 for the robust qPAH sample and 0.6 for the full sample (with p-values of ≪1). We also estimate the gas-phase metallicity (12 + log(O/H)) based on stellar masses and the z ∼ 1.5 O3N2-based mass-metallicity relation (MZR) of Topping et al. (2021) and the Pettini & Pagel (2004) calibration, shown on the top axis of Figure 7. The median trend of qPAH with the MZR-estimated metallicities closely resembles the local galaxies trend from Draine et al. (2007) (the horizontal lines in Figure 7, left). The two qPAH median values of the local galaxies were reported at metallicities below and above 12 + log(O/H) = 8.1. The rapid change in qPAH happens at ∼0.1 − 0.2 dex higher oxygen abundances in our z ∼ 1.3 sample compared to that at z ∼ 0. However, given the uncertainties in metallicity calibrations (see also the next section), we conclude that the behaviour of the z ∼ 1.3 sample is consistent with that at z ∼ 0.

There is a large scatter in qPAH at intermediate masses, such that in the mass range of log(M*/M⊙)∼9.5 − 10.5, there are galaxies with qPAH of < 0.5% to > 4%. The majority of these galaxies seem to have young ages and high specific SFRs (sSFR). To better understand the physical process driving the scatter, we also calculate partial correlation coefficients between qPAH, M*, and a third galaxy parameter, including sSFR, SFR, age, optical depth, obscured SFR fraction, and SFR surface density. However, we do not find a significant secondary dependence on any of these parameters in the qPAH − M* correlation of the robust sample. If we limit the sample to only qPAH values with > 3σ significance, the specific SFR (sSFR) and age reduce the qPAH − M* correlation coefficient of 0.4 to a partial coefficient of 0.25, indicating a potential secondary influence on the qPAH − M* correlation, such that at a given stellar mass, galaxies with higher sSFRs and younger ages have lower PAH strengths.

3.2. Polycyclic aromatic hydrocarbon fraction versus metallicity from z ∼ 0 to 2

The relation between the PAH fraction and metallicity has been extensively studied in the local Universe (Marble et al. 2010; Engelbracht et al. 2005; Madden et al. 2006; Smith et al. 2007; Galliano et al. 2008; Draine et al. 2007; Rémy-Ruyer et al. 2015; Aniano et al. 2020; Li 2020; Chastenet et al. 2023) and also at cosmic noon (Shivaei et al. 2017, using Spitzer data). To investigate this relation with the deeper MIRI data at z > 0, we estimate metallicities from the fundamental metallicity relation (FMR) between stellar mass, SFR, and metallicity. The FMR is shown to be established and invariant up to z ∼ 3 (Cresci et al. 2019; Sanders et al. 2021). Sanders et al. (2021) estimated the scatter in 12 + log(O/H) from FMR to be 0.06 dex at z ∼ 2.3, and 0.04 dex at z ∼ 0. This is typically smaller (or at most comparable) to the systematic uncertainty in strong-line metallicity calibrations (e.g. ∼0.2 dex average systematic uncertainty between the Pettini & Pagel 2004 and the Pilyugin & Thuan 2005 calibrations in Aniano et al. 2020, see their Figure 1). We adopt the FMR presented in Sanders et al. (2021) to estimate metallicities from our mass and SFR values. The adopted FMR is in agreement with those derived from direct-method metallicities (Andrews & Martini 2013) and also with the best-fit for local galaxies in Curti et al. (2020). We adopt a Monte Carlo simulation by randomly perturbing stellar mass and SFR within their uncertainties for 500 times, and derive the metallicities according to the FMR relation. The final metallicity and uncertainty of each object is the median and standard deviation of the 500 realisations. The average measurement uncertainty of the inferred 12 + log(O/H) is 0.04 dex, comparable to the FMR scatter in 12 + log(O/H).

We limit the z ∼ 0 comparison samples to two studies that adopted, similar to this study, the Draine & Li (2007) models to derive qPAH and have homogeneous metallicity calculations: Aniano et al. (2020) (hereafter, A20) and Rémy-Ruyer et al. (2015) (hereafter, R15). A20 used two strong-line metallicity calibrations for the KINGFISH sample: (1) the ‘PT’ or Pilyugin & Thuan (2005) method, adopted from Moustakas et al. (2010), and (2) the ‘PP04’ or Pettini & Pagel (2004) based on [NII]/Hα. They showed that the two metallicities can differ by as much as 0.4 dex (on average ∼0.2 dex), reflecting the large uncertainty in the calibrations. R15 incorporated the Dwarf Galaxy Survey (DGS; Madden et al. 2013) into the KINGFISH which extended the sample to lower metallicities. They adopted the PT metallicity calibration.

Figure 8 shows the qPAH trend with metallicity. There is a positive correlation (Pearson ρ = 0.55 with p-value ≪ 1) with a large scatter at high metallicities. The trend is very similar to the z ∼ 0 trend from A20 (assuming their preferred PP04 metallicity3). A20 approximated the qPAH-metallicity behaviour by both a linear function and a step function. The median values below and above their threshold metallicity, 12 + log(O/H) ∼ 8.25, and the slopes of the linear fits (3.6 ± 0.7 and 4.0 ± 0.5 at z ∼ 0 and 1.3, respectively) for the two samples suggest a non-evolving PAH fraction-metallicity relation from z ∼ 0 − 2.

thumbnail Fig. 8.

PAH mass fraction versus metallicity. Metallicity was derived from the FMR of Sanders et al. (2021). The robust and low-confidence qPAH samples (Section 2.2) are shown with larger and smaller circles, respectively. We provide the values of the robust sample in Table 1. The z ∼ 0 data from Aniano et al. (2020) are shown in red. Following the analysis of Aniano et al. (2020), we fit both samples with a linear function, shown with solid lines (slopes of 3.63 ± 0.71 and 4.04 ± 0.51 and intercepts of −28.60 ± 6.14 and −31.94 ± 4.38 for the z ∼ 0 and 1.3 sample, respectively). The medians of the two samples below and above 12 + log(O/H) = 8.25 (dotted lines) are also shown. The two samples follow very similar trends. The average scatter in 12 + log(O/H) from FMR (0.05 dex, see text) and the strong-line metallicity calibration uncertainty for the z ∼ 0 sample (0.2 dex; Aniano et al. 2020) are shown in the bottom right. The error bars on the z ∼ 1.3 data are the metallicity measurement uncertainties from the SFR and mass uncertainties. The linear fits (solid lines) have slopes of 3.6 and 3.4 for the z ∼ 0 and 1.3 samples, respectively.

In Figure 9 (top panel), we compare our results with the z ∼ 0 data over a wider range of metallicities by combining both the A20 and R15 data (using the PT metallicity). The qPAH values of R15 extend to larger values compared to A20 and ours, because they set a higher upper limit for the qPAH prior in their fittings. We also include A20 data for the PP04 metallicity, for completeness. To interpret and compare the datasets, we adopt a moving (running) median to smooth the data without assuming a parametric functional form a priori. All three trends show a constant low (≲1%) qPAH at low metallicities (12 + log(O/H) ≲ 8.1 − 8.2 or ∼0.3 Z⊙ assuming 12 + log(O/H) = 8.69 for Solar metallicity; Asplund et al. 2009), then a linear increase in qPAH with metallicity that ends with a plateau (qPAH ∼ 3.4%) at 12 + log(O/H) ≳ 8.4 (≳0.5 Z⊙). We show the fits to the moving medians in the lower panel of Figure 9. The constant qPAH at high metallicities confirms the successful usage of PAH strengths as IR luminosity and obscured SFR indicators for moderately massive and metal-rich galaxies based on local calibrations (e.g. Calzetti et al. 2007; Shipley et al. 2016). Our findings are also in general agreement with Marble et al. (2010) based on the z ∼ 0 SINGS data, who found a linear relation between PAH luminosity fraction and metallicity. These observations show that, at least up to z ∼ 2, metallicity is a good indicator of the ISM properties that affect the balance between the formation and destruction of PAHs in star-forming galaxies, and the responsible processes maintain a constant PAH abundances of ∼3.4% above a metallicity of ∼0.5 Z⊙.

thumbnail Fig. 9.

PAH mass fraction as a function of metallicity at z ∼ 1.3 (this work) and z ∼ 0 (Aniano et al. 2020; Rémy-Ruyer et al. 2015). Here, we only include the robust qPAH sample at z ∼ 0.7 − 2.0. Top: The z ∼ 1.3 data presented in this work is shown with orange circles. The orange line shows the moving median. Metallicity of the z ∼ 1.3 sample is estimated using the FMR relation of Sanders et al. (2021). The z ∼ 0 data is shown for the PP04 metallicity calibrations of Aniano et al. (2020) (purple diamonds, and purple line for the moving median) and the PT metallicity calibrations of Aniano et al. (2020) and Rémy-Ruyer et al. (2015) (green squares, and the green line for the moving median). The Rémy-Ruyer et al. (2015) data extend the z ∼ 0 sample to much lower metallicities. The two metallicity calibrations are systematically different (on average ∼0.2 dex but can be up to 0.4 dex); therefore, we show both for completeness. Bottom: Three-step fits (constant+linear+constant) to the moving median trends in the top panel. The shaded regions show the error in the mean in each consecutive bin of the moving median. Despite the uncertainties in metallicities, the overall qPAH-metallicity behaviour of the z ∼ 0 and z ∼ 1.3 samples are similar within the scatter.

Below ∼0.5 Z⊙, we see that there is a linear decrease in the PAH fraction, which has a similar slope between the z ∼ 0 and 1.3 samples. This universal PAH fraction-metallicity relation can potentially be calibrated to estimate the metallicities of metal-poor galaxies at high redshifts using IR imaging surveys alone. The source of the decreasing PAH fraction with decreasing metallicity can be explained by the destruction of PAHs at low metallicities, either through radiative destruction in less shielded low-metallicity environments (Madden et al. 2006; Hunt et al. 2010; Narayanan et al. 2023), or supernova shocks (Seok et al. 2014). Some studies also explain it by insufficient production of PAHs due to a delayed injection into the ISM by AGB stars (Galliano et al. 2008) or more efficient production at high metallicities through shattering of large grains (Seok et al. 2014). Future cosmological simulations with on-the-fly dust evolution simulations can shed light on the complex interplay of the formation and destruction processes of these grains in the ISM.

3.3. Polycyclic aromatic hydrocarbon fraction and other galaxy parameters

In Figure 10 we show qPAH as a function of other galaxy parameters: age, SFR, stellar mass, obscured luminosity fraction (fobscured), and SFR surface density (ΣSFR). Obscured luminosity fraction is calculated as the ratio of the dust-obscured UV (1550 Å) luminosity to the intrinsic UV luminosity (see Section 4). Sizes are calculated in the F1500W filter, tracing rest-frame 5 to 9 μm dust emission, for galaxies with spatially resolved profiles (see Section 2.4). In the literature, ΣSFR is often calculated based on the area derived from a shorter-wavelength size measurement that is not a good proxy for where the bulk of the stars are forming. Here, surface area is based on dust sizes (from F1500W) that closely reflects the star-forming region, and hence, the resulting SFR surface densities are more reliable.

thumbnail Fig. 10.

PAH mass fraction as a function of galaxy parameters. From top-left to bottom-right: age of the galaxy, SFR, stellar mass, obscured luminosity fraction, SFR surface density (using F1500W sizes). The robust sample is shown with a teal colour and the low-confidence sample with smaller grey symbols (see Section 2.2 for sample definitions). The moving medians of the full (robust+low-confidence) and robust samples are shown as grey and black curves, respectively. In the bottom row, the unresolved sources in F1500W images are shown with triangles as lower limits on SFR surface density. Among the parameters show, qPAH has the strongest correlations with mass, age, and obscured luminosity fraction.

We show the moving medians for the robust (black curve) and the full sample (grey curve), which includes the robust sample, in Figure 10. In the robust sample, qPAH correlates with age, stellar mass, and obscured fraction. The qPAH-mass correlation is the strongest among these, and is likely a byproduct of the mass-metallicity relation (as was discussed in previous sections). The correlation with age can be expected as a stellar evolutionary effect if the AGB stars are the primary production channel of PAHs (Galliano et al. 2008; Li 2020) and, in fact, it is also seen at z ∼ 2 from MIPS data (Shivaei et al. 2017). However, this correlation disappears when the full sample is considered. The correlation with obscured fraction is interesting as it may suggest PAH destruction due to reduced shielding by dust grains in systems with low obscured fractions. We also note the lack of a significant correlation with SFR surface densities for the spatially resolved galaxies, which may suggest that the fraction of PAH-to-total dust mass is insensitive to the star formation intensity. Even including lower limits on SFR surface density for the unresolved sources (triangles in Figure 10) does not suggest a correlation with SFR surface density. Further analysis of this trend using size measurements from other filters that have higher resolution but still trace the dust emission will be done in a future work.

4. Dust-obscured luminosity fraction

The largest uncertainty in measuring SFR is the fraction of dust-obscured star formation. The most reliable and direct method of accounting for the dust-obscured fraction is observing the dust thermal emission in IR. With Spitzer and Herschel, both sensitivity and confusion noise limitations have impeded our ability to calculate the obscured SFR in typical and low-mass galaxies at z ∼ 1 and above without relying on stacking many galaxies. MIRI directly traces mid-IR PAH emission up to z ∼ 3 (z ∼ 2 with the more sensitive shorter-wavelength bands). Even though converting mid-IR emission to total IR luminosity is model-dependent, its uncertainty is typically lower than that affecting the UV slope methods for moderately and highly obscured galaxies (e.g. Shivaei et al. 2020a). In this section, we estimate the obscured luminosity fraction from our UV-to-mid-IR SED fits and study its variation as a function of stellar mass and SFR surface density.

In the previous section, we showed that the PAH fraction reaches a constant average value at metallicities above ∼0.5 Z⊙, and hence using PAH luminosity to estimate total IR luminosity and obscured SFR is robust in this regime. However, as the PAH fraction changes at lower metallicities, instead of a simple PAH-to-IR luminosity conversion, we adopt the full UV-to-mid-IR energy-balanced SED fits to derive the obscured fraction as the ratio of obscured to intrinsic (total) UV luminosity at 1550 Å: f obsc = L UV obscured / L UV intrinsic = 1 − ( L UV unattenuated / L UV intrinsic ) $ f_{\mathrm{obsc}} = L^{\mathrm{obscured}}_{\mathrm{UV}}/L^{\mathrm{intrinsic}}_{\mathrm{UV}} = 1 - (L^{\mathrm{unattenuated}}_{\mathrm{UV}}/L^{\mathrm{intrinsic}}_{\mathrm{UV}}) $, where the unattenuated UV luminosity is directly constrained by the observed photometry at rest-frame UV and the intrinsic UV luminosity is estimated from the dust-free (intrinsic) best-fit SED model. Our choice of using the UV luminosity to estimate the obscured fraction is because of its multiple implications for high-redshift studies that often only have UV data, but we note that the fractions are in very close agreement with total IR to unattenuated UV luminosity (as was expected). Converting the luminosity fractions to SFR fractions require additional conversions of the luminosities to SFRs, which we decide to avoid in the current paper to mitigate uncertainties.

4.1. Relationship between obscured fraction and mass

As most of the metals in the ISM are depleted onto dust grains that attenuate starlight, it is expected that obscured luminosity fraction (ratio of attenuated to intrinsic luminosity) correlates with metallicity, and hence stellar mass (e.g. Reddy et al. 2010; Whitaker et al. 2017), which is also manifested in the relationship between dust attenuation and mass (e.g. Garn et al. 2010; Shivaei et al. 2020b; Bogdanoska & Burgarella 2020).

In Figure 11, the obscured fraction is shown as a function of stellar mass. We investigate the average shape and scatter of the relationship at M* > 4 × 108 M⊙, where the sample is complete. The mass completeness is estimated based on the detection limits of 5.6 μm and 15 μm data and assuming a mass-to-light ratio of 0.6 at 2.2 μm (McGaugh & Schombert 2014)4. To study the average trend, we fit the data in three ways: a moving median function5, the functional form of fobsc − M* suggested by Whitaker et al. (2017),

thumbnail Fig. 11.

Obscured luminosity fraction as a function of stellar mass for the full sample (left) and separated by redshift (right). Obscured fraction is defined as the obscured UV to total (intrinsic) UV luminosity at 1550 Å, inferred from the best-fit UV-to-IR SEDs. We show the moving median (dashed thick lines), moving weighted-average (dotted line) and best-fit curve (solid lines) to the samples at M* > 4 × 108 M⊙, where the data is mass-complete. In the left panel, we also show the Whitaker et al. (2017) fit to z = 0.5 − 2.5 with an orange curve. The Whitaker et al. (2017) study was based on Spitzer/MIPS data with a wider area but biased to more obscured systems. Our weighted-average trend is also dominated by the heavily obscured systems, and therefore similar to the (Whitaker et al. 2017) curve. However, the median trend that is more representative of the full population captured by the deeper MIRI data (relative to the MIPS data) is systematically lower. Furthermore, as is shown in the right panel, there is no redshift evolution in this relation in our sample.

f obscured = 1 1 + a e b log ( M ∗ / M ⊙ ) , $$ \begin{aligned} f_{\rm obscured} = \frac{1}{1+a\;e^{b\log (M_*/M_{\odot })}}, \end{aligned} $$(2)

where fobscured is the obscured fraction, and a and b are the fit parameters, and the following function that best matches the moving median trend:

f obsc = ( f max − f min ) 2 × ( erf ( log ( M ∗ / M ⊙ ) − μ 2 σ ) + 1 ) + f min , $$ \begin{aligned} f_{\rm obsc} = \dfrac{(f_{\rm max}-f_{\rm min})}{2} \times \left(\mathrm{erf}\left(\dfrac{\log (M_*/M_{\odot })-\mu }{\sqrt{2}\;\sigma }\right)+1\right) + f_{\rm min}, \end{aligned} $$(3)

where erf is the error function, and fmax, fmin, μ, and σ are the fitting parameters. Using an orthogonal distance regression (ODR) fitting procedure (python scipy.odr), considering the uncertainties on both the obscured fraction and mass, the fit using Equation (2) matches the Whitaker et al. (2017) curve closely. However, our fit is highly biased by the few highly obscured galaxies with very small uncertainties. The moving (running) weighted-average curve, where the weight is the inverse square of uncertainty in fobsc, also shows how this small population of highly obscured galaxies bias the fit (dotted curve in Figure 11). The running median (dashed curve) and the Equation (3) fit (black line) better represent the behaviour of fobsc as a function of mass. The best fit parameters are listed in Table 2.

Table 2.

Best-fit parameters of fobscured − M* for the full sample in Equation (3).

We do not see any significant redshift evolution in this relation, as is shown in the right panel of Figure 11, in agreement with the findings of Whitaker et al. (2017) that at a fixed mass the obscured fraction is constant from z ∼ 0.5 to 2.5. Based on our best-fit curve (Eq. 3) that matches the moving median, on average, the UV luminosity is dominantly obscured (fobsc > 50%) above the stellar mass of ∼5 × 109 M⊙. Interestingly, owing to the large scatter in fobsc at any mass, there are galaxies with dominantly obscured emission even down to M* ∼ 5 × 108 M⊙. We investigate the scatter in fobsc at fixed mass in the next section. Above the stellar mass of 2 × 1010 M⊙, more than 80% of the emission is obscured. However, the SMILES survey is likely not representative of the population of heavily obscured (and rare) galaxies owing to its relatively small area.

Whitaker et al. (2017) studied the Spitzer/MIPS samples and found that the fobscured − M* relation does not change from z = 0 to 2.5. They fit the UV-near-IR photometry with Bruzual & Charlot (2003) models and used the Dale & Helou (2002) template to convert 24 μm flux densities to total IR luminosities. Then assuming the Kennicutt (1998) and Bell et al. (2005) calibrations, they converted UV and IR luminosities to SFRs to estimate f obsc = SFR IR SFR IR + SFR UV $ f_{\mathrm{obsc}} = \frac{\mathrm{SFR_{IR}}}{\mathrm{SFR_{IR}+SFR_{UV}}} $. While the two relationships are in relatively good agreement within the scatter of the relation in Figure 11, there are a few differences between the Whitaker et al. (2017) study and this work that contribute to some disagreement between the two relationships. Whitaker et al. (2017) used a single log-averaged IR template from Dale & Helou (2002) (i.e. a fixed IR SED shape) to convert PAH luminosity to total IR luminosity for their sample at z ∼ 0.5 − 2.5. While at high metallicities and masses, galaxies may have a more uniform IR SED shape, and hence, the assumption of a single IR SED would be valid, that is not always the case at low metallicities. As we showed in the previous section, below ∼0.5Z⊙ the PAH fraction decreases uniformly from z ∼ 0 − 2. Therefore, using the high-metallicity end calibrations would overestimate the IR luminosities at lower metallicities (and masses; see also e.g. Shivaei et al. 2017, 2022). Therefore, the single IR SED assumption in Whitaker et al. (2017) might have overestimated their IR luminosity values at lower masses. Additionally, the different area and sensitivity of SMILES compared to the MIPS/Spitzer surveys can play a role in the observed discrepancy between this study and the Whitaker et al. (2017) study. SMILES is more sensitive to less obscured galaxies at a fixed mass relative to the MIPS samples. In fact, the fit to our data using the Whitaker et al. (2017) formalism and an ODR fitting procedure (i.e. taking into account the uncertainties on fobsc) closely follows the Whitaker et al. (2017) curve. This is because a few highly obscured galaxies with very low fobsc uncertainties dominate the fit – a similar bias that a MIPS-based sample would have. Furthermore, SMILES has a smaller area compared to the Spitzer/MIPS surveys, and hence, is likely missing a (rarer) population of massive and highly attenuated galaxies.

4.2. Scatter in fobsc–M* and relationship with ΣSFR

As was mentioned in the previous section, there is a large scatter in fobsc at a given mass, such that there are galaxies with significant obscured UV emission down to stellar masses of ∼5 × 108 M⊙. The scatter in the obscured fraction at a given mass increases from 0.1 dex at M* ∼ 1011 M⊙ to ∼0.5 dex at M* ∼ 109 M⊙. We calculate secondary correlations in the fobsc − M* relation with sSFR, age, and SFR surface density using partial correlation coefficients. The surface density is measured using dust sizes from F1500W data (Section 2.4). In those calculations the sample is limited to galaxies with spatially resolved discs in F1500W. The spatially resolved sample is limited to galaxies with M* > 109.5 M⊙, and inevitably biased against the extremely compact star-forming galaxies. The stellar mass distribution of the spatially resolved sample above M* > 109.5 M⊙ is very similar to that of the parent sample with 50% of the spatially resolved sample at M* < 1010.2 M⊙. Among the sSFR, age, and SFR surface density parameters, we find a relatively strong correlation between the obscured fraction and SFR surface density at a fixed stellar mass, but no significant correlations with age and SFR at constant mass.

Figure 12 shows the obscured fraction versus SFR surface density (ΣSFR, left) and F1500W effective radii (middle). ΣSFR is calculated using dust surface area (at rest-frame 8 − 9 μm) that closely traces the active star-forming region. We divide the sample in three stellar mass bins to investigate the trend at a fixed mass. The average values are shown with large symbols in the figure.

thumbnail Fig. 12.

Obscured luminosity fraction as a function of ΣSFR (using F1500W sizes) and F1500W effective radius (middle) for the F1500W spatially resolved sample (the filter FWHM is 0.5 arcsec). At a given mass, fobsc increases with ΣSFR and decreases with rest-frame mid-IR (dust) radii. Right panel shows SFR versus F1500W size for the same sample. The near constant SFR with Re, F1500W in each mass bin indicates that the relationship between fobsc and size is independent of SFR. Individual measurements are shown with small symbols and colour-coded in three stellar mass bins with the same number of galaxies, shown in the legend. In each mass bin, average values in bins of the parameter on the x axis are shown with larger symbols with the corresponding shape and colour of the mass bin. Pearson correlation coefficients (ρ) are shown in the corners of the plots with corresponding colours of each mass bin. Linear fits to the average values of fobsc versus log(ΣSFR) are shown in the left panel. The fit parameters are in Table 3.

There is a clear correlation between fobsc and ΣSFR at all masses with Pearson correlation coefficient of ∼0.5 (p-value ≪ 1). We fit the average trends in each mass bin with a linear function. As was expected, the overall normalisation increases with increasing mass; that is, as was shown in the previous figures, fobsc increases with increasing mass. However, not only does fobsc clearly increase with ΣSFR (and decreases with size) at a given mass, but the rate at which fobsc increases with ΣSFR (i.e. the slope) appears to be similar across the mass range of the sample. The fit parameters are presented in Table 3. We discuss the possible explanation of this behaviour in the next Section. While the overall trend with size (effective radius) is consistent, the slope of the fobsc-size relation varies among the three mass bins and the evolutionary behaviour is not as clear as with ΣSFR. We also note that the width of the fobsc distribution decreases as the mass increases, as is shown with the error bars on the average values in Figure 12. The standard deviation of fobsc in the highest ΣSFR bin from low to high mass is 0.20, 0.15, 0.07, respectively.

Table 3.

Fit parameters of the linear fits in Figure 12.

The right panel of Figure 12 confirms that the fobsc increasing trend with ΣSFR is not a byproduct of increasing SFR. While there is a general correlation between SFR and size for the full sample, the average SFR does not vary with size in the fixed mass ranges. Therefore, the underlying cause of fobsc dependence on ΣSFR at a given mass is the compactness of the star-forming region, and not only an increase in the rate of star formation.

4.3. Morphological evolution and obscured fraction

Using submm or mm data for samples with generally much higher stellar masses and SFRs than presented here, studies have shown that star formation occurs in more compact regions compared to the stellar mass sizes (e.g. Murphy et al. 2017; Jiménez-Andrade et al. 2021; Hodge et al. 2016; Elbaz et al. 2018; Fujimoto et al. 2017; Rujopakarn et al. 2019; Hamed et al. 2023a). Additionally, it has been argued that starburst galaxies on the main-sequence with particularly short depletion timescales exhibit higher SFR surface densities with more compact mm dust emission (Elbaz et al. 2018; Gómez-Guijarro et al. 2022) and radio emission (Jiménez-Andrade et al. 2019), and hotter dust (Gómez-Guijarro et al. 2022) compared to other main-sequence galaxies at the same mass and redshift. In the regime of lower SFR surface density (log(ΣSFR/M⊙yr−1 kpc−2)∼ − 1 to 1) and mass (log(M*/M⊙)∼9.5 to 11), we observe the same relation for purely star-forming galaxies (no AGN contamination) that PAH dust sizes are more compact with higher SFR surface densities at a fixed mass (right panel of Figure 12).

We also see that the obscured emission is more dominant in compact galaxies with higher ΣSFR. This observed trend is illustrated by a simple cartoon in Figure 13. For an extended star-forming galaxy the dust-star geometry is more complex: some population of stars are only affected by the diffuse ISM dust, while others can be trapped in their birthcloud dust and highly attenuated. If the star-forming region is compressed into a small area, the galaxy will have a more homogeneous dust distribution with higher covering fraction that attenuates most of the light emitted from the stars. Hence, the obscured fraction of the emitted light is higher in galaxies with compact star-forming regions. This explanation works for closed-box systems. However, strong outflows and feedback may clear pathways through the ISM of the compact star-forming regions and expose the starlight without attenuation. This may explain the larger variation in fobsc in the low mass bins at any ΣSFR: low-mass galaxies have highly stochastic star formation histories (Hopkins et al. 2014), and massive stars produced in the vigorous starbursts can destroy their birth clouds via feedback (e.g. winds, supernovae; Naidu et al. 2022) to make sightlines clear of dust. This will generate a diversity of fobsc from galaxy to galaxy at low masses, while in massive galaxies dust stays in the compact core with high covering fraction. In our data, the scatter (standard deviation) of fobsc in the lowest mass bin is 15 − 20% at a fixed ΣSFR and decreases to 8 − 12% in the highest mass bin.

thumbnail Fig. 13.

Cartoon illustrating a physical explanation of the correlation between fobsc and star-forming compactness. Stars are shown in blue. Diffuse ISM dust is shown with light red and the ‘birth cloud’ dust with higher column density is shown with a darker red colour. Schematically, less and more dust-obscured light (i.e. obscured by the low and high column density dust, respectively) are shown with blue and red arrows, respectively, reaching to the observer on the right. Extended galaxies have a range of dust-star geometries, while compact galaxies contain most of their stellar population in the core with high dust covering fraction, resulting in most of the emitted starlight being obscured by dust.

The relationship of obscured fraction with compactness of star-forming region can also explain the spread in the locus of galaxies in the IRX-β diagram. The IRX-β relation is an empirical calibration of UV stellar continuum slope (β) based on the ratio of IR to unobscured UV luminosity (IRX; Meurer et al. 1999). The location of galaxies in this diagram depends on the slope of the attenuation curve in the UV and the intrinsic UV slope (e.g. Reddy et al. 2018; Shivaei et al. 2020a; Salim & Narayanan 2020; Hamed et al. 2023b). Figure 14 shows the distribution of our sample in the IRX-mass and IRX-β diagrams. Galaxies with higher ΣSFR at a given mass or β have higher IRX, and preferentially shallower attenuation curves similar to that of the Calzetti et al. (2000) curve (middle panel; similar trends are also seen at z ∼ 0, Johnson et al. 2007). The preference for shallower curves is potentially due to both a higher average optical depth and a lower fraction of unobscured evolved stars. Radiative transfer models have shown that a high dust optical depth flattens the dust attenuation curve (Chevallard et al. 2013) and the right panel of Figure 14 shows that ΣSFR in our sample is correlated with the dust optical depth (Pearson ρ = 0.65 with p-value ≪ 1). Additionally, as is shown in the schematic Figure 13, galaxies with more concentrated star-forming regions (higher ΣSFR) have lower fraction of evolved stars unobscured by dust, as these stars would not have sufficient time to migrate away from their dusty birth clouds. This dust-star geometrical effect also tends to flatten the dust attenuation curve of galaxies in which the evolved stars dominate the optical luminosity (Narayanan et al. 2018). The inclination (axis ratio) of galaxies can also play a role in the observed trends, which will be investigated in future studies.

thumbnail Fig. 14.

IRX (ratio of IR to UV 1550 Å luminosity) as a function of stellar mass (left panel) and UV stellar continuum slope (middle panel). Galaxies with spatially resolved morphology in F1500W are colour-coded by their ΣSFR. A linear fit to log(IRX)−log(M*/M⊙) is shown in the left panel (slope of 0.96 ± 0.06 and intercept of −8.47 ± 0.61). In the middle panel, we show three IRX-β relations in the literature adopted from Reddy et al. (2018) assuming a constant star formation history and an age of 100 Myr for stellar populations: the original Meurer et al. (1999) relation, the starburst curve of Calzetti et al. (2000) and the SMC curve of Gordon et al. (2003) assuming 0.14 Solar metallicity. A higher metallicity system will result in a redder intrinsic UV slope (β0), shifting the curves to the right of the diagram (e.g. the Calzetti curve for a 1.4 Z⊙ population and β0 = −2.4 resembles the Meurer et al. 1999 curve). Galaxies with higher ΣSFR at a given mass or β have higher IRX and a shallower attenuation curve. Right panel: V-band dust optical depth versus ΣSFR, colour-coded with the attenuation curve slope defined as the deviation from the Calzetti et al. (2000) (the formalism of Kriek & Conroy 2013), where zero is the Calzetti curve slope. The two parameters are highly correlated with ρ = 0.65 (p-value ≪ 1). The shallower attenuation curve of galaxies with high IRX at a given mass or β can be explained by the radiative transfer effects that are a result of their high ΣSFR: higher optical depths and lower fractions of unobscured evolved stars.

5. Conclusions

In this study, we have used SMILES, the largest 5−25 μm MIRI survey in the first two observing cycles of JWST, to study the dust-obscured and PAH grain properties of 443 galaxies at z = 0.7 − 2.0 (median redshift of z ∼ 1.3), in which 216 of them have well-constrained qPAH values, dubbed the ‘robust qPAH’ sample. The exceptional sensitivity, angular resolution, and mid-IR wavelength coverage offered by SMILES enables unambiguous detection of dust emission from star-forming regions in galaxies, reaching mass and SFR an order of magnitude lower than was achievable with JWST’s predecessor, Spitzer. Augmented by the deep NIRCam (JADES) and HST (CANDELS) data in GOODS-S, we performed SED fitting on the extremely well-covered photometry spanning from rest-frame UV to mid-IR. We have studied the PAH to dust mass fractions (qPAH) and dust-obscured fraction of UV luminosity (fobsc) in relation to galaxy parameters such as stellar mass, metallicity, and SFR surface density. The sample contains main-sequence galaxies spanning a range from ∼108.4 − 1011.3 M⊙. Our key findings are summarised below.

  • We find a strong correlation between the mass fraction of dust in PAHs (i.e. PAH mass fraction or qPAH) and stellar mass. A similar correlation is seen between the PAH luminosity fraction relative to the total IR luminosity and mass. This correlation positions the qPAH value of the majority of galaxies at z ∼ 1.3 between the median values of low- and high-metallicity galaxies at z ∼ 0 (Draine et al. 2007).

  • Using the FMR, we estimated the gas metallicity of the sample and compared the qPAH-metallicity relation at z ∼ 1.3 with that at z ∼ 0. Despite the uncertainties in the z ∼ 0 metallicities due to strong line calibrations (∼0.2 dex, Aniano et al. 2020 compared to the ∼0.05 dex metallicity scatter from the FMR), we observe a strong agreement in the qPAH-metallicity trends from z ∼ 0 to 2. In this relationship, qPAH remains relatively constant at ∼3.4% above ∼0.5 Z⊙, confirming the reliability of PAH luminosity as a robust calibrator for estimating the total IR luminosity (and similarly, the PAH mass to dust mass) in metal-rich galaxies. Below 0.5 Z⊙, the PAH fraction declines sharply, reaching a very low value of < 1% at metallicities below 0.3 Z⊙. This redshift-invariant nature of the qPAH-metallicity relation below ∼0.5 Z⊙ could potentially serve as a basis for calibrating the PAH luminosity fraction as a metallicity indicator in this range. This would be an efficient way of estimating metallicities from relatively cost-effective imaging surveys, with MIRI applicable up to z ∼ 2 and potential future far-IR probes such as SPICE (Urry et al. 2023; Bonato et al., in prep.) or PRIMA (Moullet et al. 2023) extending capabilities to z ∼ 7.

  • We observe a strong correlation between the fraction of obscured UV emission (the ratio of obscured to total UV luminosity) and stellar mass that does not change with redshift. Galaxies with stellar masses above 109.6 M⊙ have, on average, more than half of their light obscured by dust. In the stellar mass range of ∼108.5 to 1011 M⊙, the obscured fraction increases from ∼15% to more than 90%.

  • We determined dust sizes using F1500W images, which capture the ∼5 − 8.8 μm dust and PAH emission within the redshift range of z = 0.7 − 2. The spatial resolution of MIRI allows us to obtain sizes of galaxies at stellar masses ∼109 − 11 M⊙ (the median mass within the spatially resolved sample is 1010 M⊙). Our findings indicate that, at a given mass, galaxies with compact dust regions (indicative of active star formation) exhibit higher SFR surface densities (ΣSFR). This suggests shorter depletion timescales in compact galaxies. Additionally, at the same mass, galaxies with higher ΣSFR also exhibit higher obscured luminosity fractions. However, among lower-mass galaxies there is a broader range of fobsc at a fixed ΣSFR.

  • We explain the observed correlation between fobsc and ΣSFR at a constant mass by attributing it to the increase in the dust covering fraction as the star-forming region becomes more compact. Simultaneously, the observed increase in the scatter of fobsc at low masses compared to that in more massive bins can be attributed to the more bursty nature of star formation in lower-mass galaxies. Feedback mechanisms may contribute to the wider range of dust covering fractions at low masses for a given ΣSFR.

  • Similarly, we find that for a given mass or UV continuum slope (β), galaxies with higher attenuation quantified by the IRX (IR to unobscured UV luminosity) parameter tend to possess higher ΣSFR, positioning them within the region of the IRX-β diagram that aligns with shallower attenuation curves. Such shallow attenuation curves may arise from both elevated average dust optical depths and a compact dust-star geometry (with reduced fraction of unobscured evolved stars) at high SFR surface densities.

We are just at the beginning of an exciting journey with MIRI to unveil the properties of dust beyond the local Universe, in an unexplored SFR-mass regime. In the future, larger samples could help to solidify the trends presented here. Additionally, more sophisticated spatial analysis of the mid-IR data, as unbiased probes of intense star formation, will be invaluable in shedding light on the morphological evolution of galaxies.

Data availability

Full table is published in an online repository: https://zenodo.org/records/12671075

1

Our derived sensitivities are ∼2 − 3× deeper than the sensitivities predicted by ETC (version 3.0) for our observation setup.

2

Online repository for supplementary data: https://zenodo.org/records/12671075

3

A20 and Hunt et al. (2016), who used the same metallicities in their analysis, preferred the PP04 calibration as it shows tighter scaling relations with other calibrations and with qPAH.

4

The exact completeness varies with redshift from 0.7 to 2.

5

The moving weighted-average fit shows an identical trend to the moving median curve.

Acknowledgments

IS thanks the members of the JWST/MIRI instrument team for their exceptional efforts and for providing an outstanding experience during the commissioning period of JWST, which fostered numerous fruitful discussions and significantly enhanced the quality of data reduction in this study. IS also thanks Karin Sandstrom and Joel Leja for their insightful discussions during the scientific development of this work. Additionally, IS acknowledges the contribution of Andras Gáspar to the construction of the F560W PSF utilised in this research. This work was supported in part by NASA grant NNX13AD82G. Part of this research has been funded by Atraccíon de Talento Grant No. 2022-T1/TIC-20472 of the Comunidad de Madrid, Spain. AJB and AC acknowledges funding from the ‘FirstGalaxies’ Advanced Grant from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant agreement No. 789056). The work of CCW is supported by NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. PGP-G acknowledges support from grant PID2022-139567NB-I00 funded by Spanish Ministerio de Ciencia e Innovación CIN/AEI/10.13039/501100011033, FEDER Una manera de hacer Europa. SA acknowledges support from the JWST Mid-Infrared Instrument (MIRI) Science Team Lead, grant 80NSSC18K0555, from NASA Goddard Space Flight Center to the University of Arizona. This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program PID 1207, 1080, 1081, 1895, 1220, 1286, 1287, 1963. Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESAC/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).

References

  1. Alberts, S., Lyu, J., Shivaei, I., et al. 2024, ApJ, submitted [arXiv:2405.15972] [Google Scholar]
  2. Álvarez-Márquez, J., Labiano, A., Guillard, P., et al. 2023, A&A, 672, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aniano, G., Draine, B. T., Hunt, L. K., et al. 2020, ApJ, 889, 150 [NASA ADS] [CrossRef] [Google Scholar]
  5. Armus, L., Lai, T., U, V., et al. 2023, ApJ, 942, L37 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ashby, M. L. N., Willner, S. P., Fazio, G. G., et al. 2015, ApJS, 218, 33 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bacon, R., Brinchmann, J., Conseil, S., et al. 2023, A&A, 670, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barrera, N. F., Fuentealba, P., Muñoz, F., Gómez, T., & Cárdenas, C. 2023, MNRAS, 524, 3741 [NASA ADS] [CrossRef] [Google Scholar]
  11. Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [Google Scholar]
  12. Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [Google Scholar]
  13. Bogdanoska, J., & Burgarella, D. 2020, MNRAS, 496, 5341 [NASA ADS] [CrossRef] [Google Scholar]
  14. Boschman, L., Cazaux, S., Spaans, M., Hoekstra, R., & Schlathölter, T. 2015, A&A, 579, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bunker, A. J., Cameron, A. J., Curtis-Lake, E., et al. 2024, A&A, in press https://doi.org/10.1051/0004-6361/202347094 [Google Scholar]
  17. Bushouse, H., Eisenhamer, J., Dencheva, N., et al. 2023, https://doi.org/10.5281/zenodo.7795697 [Google Scholar]
  18. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  19. Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [Google Scholar]
  20. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  21. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  22. Chastenet, J., Sutter, J., Sandstrom, K., et al. 2023, ApJ, 944, L11 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chevallard, J., Charlot, S., Wandelt, B., & Wild, V. 2013, MNRAS, 432, 2061 [CrossRef] [Google Scholar]
  24. Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cresci, G., Mannucci, F., & Curti, M. 2019, A&A, 627, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Curti, M., Mannucci, F., Cresci, G., & Maiolino, R. 2020, MNRAS, 491, 944 [Google Scholar]
  27. Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [Google Scholar]
  28. Dicken, D., García Marín, M., Shivaei, I., et al. 2024, A&A, 698, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Dickinson, M., & FIDEL Team 2007, BAAS, 39, 822 [NASA ADS] [Google Scholar]
  30. Dickinson, M., Giavalisco, M., & GOODS Team 2003, in The Mass of Galaxies at Low and High Redshift, eds. R. Bender, & A. Renzini, 324 [Google Scholar]
  31. Dole, H., Rieke, G. H., Lagache, G., et al. 2004, ApJS, 154, 93 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dole, H., Lagache, G., Puget, J. L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
  34. Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
  35. Draine, B. T., Li, A., Hensley, B. S., et al. 2021, ApJ, 917, 3 [CrossRef] [Google Scholar]
  36. Eisenstein, D. J., Johnson, B. D., Robertson, B., et al. 2023, ApJS, submitted [arXiv:2310.12340] [Google Scholar]
  37. Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Elbaz, D., Leiton, R., Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Engelbracht, C. W., Gordon, K. D., Rieke, G. H., et al. 2005, ApJ, 628, L29 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [Google Scholar]
  41. Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gardner, J. P., Mather, J. C., Abbott, R., et al. 2023, PASP, 135, 068001 [NASA ADS] [CrossRef] [Google Scholar]
  43. Garn, T., Sobral, D., Best, P. N., et al. 2010, MNRAS, 402, 2017 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gáspár, A., Rieke, G. H., Guillard, P., et al. 2021, PASP, 133, 014504 [CrossRef] [Google Scholar]
  45. Glasse, A., Rieke, G. H., Bauwens, E., et al. 2015, PASP, 127, 686 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022, A&A, 659, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gordon, K. D., Calzetti, D., & Witt, A. N. 1997, ApJ, 487, 625 [CrossRef] [Google Scholar]
  48. Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]
  49. Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hainline, K. N., Johnson, B. D., Robertson, B., et al. 2023, ArXiv e-prints [arXiv:2306.02468] [Google Scholar]
  51. Hamed, M., Małek, K., Buat, V., et al. 2023a, A&A, 674, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hamed, M., Pistis, F., Figueira, M., et al. 2023b, A&A, 679, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Helou, G., Malhotra, S., Hollenbach, D. J., Dale, D. A., & Contursi, A. 2001, ApJ, 548, L73 [NASA ADS] [CrossRef] [Google Scholar]
  54. Hodge, J. A., Swinbank, A. M., Simpson, J. M., et al. 2016, ApJ, 833, 103 [Google Scholar]
  55. Hopkins, P. F., Keres, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
  56. Hunt, L. K., Thuan, T. X., Izotov, Y. I., & Sauvage, M. 2010, ApJ, 712, 164 [NASA ADS] [CrossRef] [Google Scholar]
  57. Hunt, L., Dayal, P., Magrini, L., & Ferrara, A. 2016, MNRAS, 463, 2002 [NASA ADS] [CrossRef] [Google Scholar]
  58. Illingworth, G. D., Magee, D., Oesch, P. A., et al. 2013, APJS, 209, 6 [NASA ADS] [CrossRef] [Google Scholar]
  59. Jiménez-Andrade, E. F., Magnelli, B., Karim, A., et al. 2019, A&A, 625, A114 [EDP Sciences] [Google Scholar]
  60. Jiménez-Andrade, E. F., Murphy, E. J., Heywood, I., et al. 2021, ApJ, 910, 106 [CrossRef] [Google Scholar]
  61. Johnson, B. D., Schiminovich, D., Seibert, M., et al. 2007, ApJS, 173, 392 [NASA ADS] [CrossRef] [Google Scholar]
  62. Johnson, B. D., Leja, J., Conroy, C., & Speagle, J. S. 2021, ApJS, 254, 22 [NASA ADS] [CrossRef] [Google Scholar]
  63. Kashino, D., Lilly, S. J., Matthee, J., et al. 2023, ApJ, 950, 66 [CrossRef] [Google Scholar]
  64. Kennicutt, R. C. 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
  66. Kennicutt, R. C., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kirkpatrick, A., Yang, G., Le Bail, A., et al. 2023, ApJ, 959, L7 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kodra, D., Andrews, B. H., Newman, J. A., et al. 2023, ApJ, 942, 36 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kriek, M., & Conroy, C. 2013, ApJ, 775, L16 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lagache, G., Dole, H., Puget, J. L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
  71. Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [Google Scholar]
  72. Leja, J., Johnson, B. D., Conroy, C., van Dokkum, P. G., & Byler, N. 2017, ApJ, 837, 170 [NASA ADS] [CrossRef] [Google Scholar]
  73. Leja, J., Speagle, J. S., Ting, Y.-S., et al. 2022, ApJ, 936, 165 [NASA ADS] [CrossRef] [Google Scholar]
  74. Li, A. 2020, Nat. Astron., 4, 339 [CrossRef] [Google Scholar]
  75. Lin, Y.-W., Wu, C. K. W., Ling, C.-T., et al. 2024, MNRAS, 527, 11882 [Google Scholar]
  76. Lyu, J., Alberts, S., Rieke, G. H., et al. 2024, ApJ, 966, 229 [NASA ADS] [CrossRef] [Google Scholar]
  77. Madau, P. 1995, ApJ, 441, 18 [NASA ADS] [CrossRef] [Google Scholar]
  78. Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
  80. Magnelli, B., Elbaz, D., Chary, R. R., et al. 2011, A&A, 528, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Magnelli, B., Popesso, P., Berta, S., et al. 2013, A&A, 553, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Magnelli, B., Gómez-Guijarro, C., Elbaz, D., et al. 2023, A&A, 678, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Marble, A. R., Engelbracht, C. W., van Zee, L., et al. 2010, ApJ, 715, 506 [NASA ADS] [CrossRef] [Google Scholar]
  84. Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
  85. McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [Google Scholar]
  86. Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]
  87. Morrison, J. E., Dicken, D., Argyriou, I., et al. 2023, PASP, 135, 075004 [NASA ADS] [CrossRef] [Google Scholar]
  88. Moullet, A., Kataria, T., Lis, D., et al. 2023, ArXiv e-prints [arXiv:2310.20572] [Google Scholar]
  89. Moustakas, J., Kennicutt, R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
  90. Murphy, E. J., Momjian, E., Condon, J. J., et al. 2017, ApJ, 839, 35 [Google Scholar]
  91. Naidu, R. P., Matthee, J., Oesch, P. A., et al. 2022, MNRAS, 510, 4582 [CrossRef] [Google Scholar]
  92. Narayanan, D., Conroy, C., Davé, R., Johnson, B. D., & Popping, G. 2018, ApJ, 869, 70 [Google Scholar]
  93. Narayanan, D., Smith, J. D. T., Hensley, B. S., et al. 2023, ApJ, 951, 100 [NASA ADS] [CrossRef] [Google Scholar]
  94. Oesch, P. A., Brammer, G., Naidu, R. P., et al. 2023, MNRAS, 525, 2864 [NASA ADS] [CrossRef] [Google Scholar]
  95. Peeters, E., Spoon, H. W. W., & Tielens, A. G. G. M. 2004, ApJ, 613, 986 [NASA ADS] [CrossRef] [Google Scholar]
  96. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
  97. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [Google Scholar]
  98. Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [Google Scholar]
  99. Pérez-González, P. G., Barro, G., Rieke, G. H., et al. 2024, ApJ, 968, 4 [CrossRef] [Google Scholar]
  100. Perrin, M. D., Soummer, R., Choquet, É., et al. 2014, SPIE Conf. Ser., 9143, 914309 [NASA ADS] [Google Scholar]
  101. Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
  102. Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [CrossRef] [Google Scholar]
  103. Reddy, N. A., Steidel, C. C., Pettini, M., et al. 2008, ApJS, 175, 48 [CrossRef] [Google Scholar]
  104. Reddy, N. A., Erb, D. K., Pettini, M., Steidel, C. C., & Shapley, A. E. 2010, ApJ, 712, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  105. Reddy, N., Dickinson, M., Elbaz, D., et al. 2012, ApJ, 744, 154 [NASA ADS] [CrossRef] [Google Scholar]
  106. Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]
  107. Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2015, A&A, 582, A121 [Google Scholar]
  108. Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [Google Scholar]
  109. Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
  110. Rieke, G. H., Wright, G. S., Böker, T., et al. 2015, PASP, 127, 584 [NASA ADS] [CrossRef] [Google Scholar]
  111. Rieke, M. J., Robertson, B., Tacchella, S., et al. 2023, ApJS, 269, 16 [NASA ADS] [CrossRef] [Google Scholar]
  112. Rieke, G., Alberts, S., Shivaei, I., et al. 2024, ApJ, submitted [arXiv:2406.03518] [Google Scholar]
  113. Rigby, J. R., Lightsey, P. A., García Marín, M., et al. 2023, PASP, 135, 048002 [NASA ADS] [CrossRef] [Google Scholar]
  114. Robertson, B., Johnson, B. D., Tacchella, S., et al. 2024, ApJ, 970, 31 [NASA ADS] [CrossRef] [Google Scholar]
  115. Rujopakarn, W., Rieke, G. H., Weiner, B. J., et al. 2013, ApJ, 767, 73 [NASA ADS] [CrossRef] [Google Scholar]
  116. Rujopakarn, W., Daddi, E., Rieke, G. H., et al. 2019, ApJ, 882, 107 [NASA ADS] [CrossRef] [Google Scholar]
  117. Salim, S., & Narayanan, D. 2020, ARA&A, 58, 529 [NASA ADS] [CrossRef] [Google Scholar]
  118. Sanders, R. L., Shapley, A. E., Jones, T., et al. 2021, ApJ, 914, 19 [CrossRef] [Google Scholar]
  119. Sandstrom, K. M., Koch, E. W., Leroy, A. K., et al. 2023, ApJ, 944, L8 [NASA ADS] [CrossRef] [Google Scholar]
  120. Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Seok, J. Y., Hirashita, H., & Asano, R. S. 2014, MNRAS, 439, 2186 [NASA ADS] [CrossRef] [Google Scholar]
  122. Shen, L., Papovich, C., Yang, G., et al. 2023, ApJ, 950, 7 [NASA ADS] [CrossRef] [Google Scholar]
  123. Shipley, H. V., Papovich, C., Rieke, G. H., Brown, M. J. I., & Moustakas, J. 2016, ApJ, 818, 60 [NASA ADS] [CrossRef] [Google Scholar]
  124. Shivaei, I., Reddy, N. A., Steidel, C. C., & Shapley, A. E. 2015, ApJ, 804, 149 [NASA ADS] [CrossRef] [Google Scholar]
  125. Shivaei, I., Reddy, N. A., Shapley, A. E., et al. 2017, ApJ, 837, 157 [NASA ADS] [CrossRef] [Google Scholar]
  126. Shivaei, I., Darvish, B., Sattari, Z., et al. 2020a, ApJ, 903, L28 [NASA ADS] [CrossRef] [Google Scholar]
  127. Shivaei, I., Reddy, N., Rieke, G., et al. 2020b, ApJ, 899, 117 [NASA ADS] [CrossRef] [Google Scholar]
  128. Shivaei, I., Popping, G., Rieke, G., et al. 2022, ApJ, 928, 68 [NASA ADS] [CrossRef] [Google Scholar]
  129. Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007, ApJ, 656, 770 [Google Scholar]
  130. Thrower, J. D., Jørgensen, B., Friis, E. E., et al. 2012, ApJ, 752, 3 [NASA ADS] [CrossRef] [Google Scholar]
  131. Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [Google Scholar]
  132. Topping, M. W., Shapley, A. E., Sanders, R. L., et al. 2021, MNRAS, 506, 1237 [CrossRef] [Google Scholar]
  133. Urry, C. M., Bonato, M., Leisawitz, D., et al. 2023, AAS/High Energy Astrophysics Division, 55, 103.78 [Google Scholar]
  134. Walter, F., Decarli, R., Aravena, M., et al. 2016, ApJ, 833, 67 [Google Scholar]
  135. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
  136. Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [Google Scholar]
  137. Whitaker, K. E., Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]
  138. Williams, C. C., Tacchella, S., Maseda, M. V., et al. 2023, ApJS, 268, 64 [NASA ADS] [CrossRef] [Google Scholar]
  139. Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
  140. Wright, G. S., Rieke, G. H., Glasse, A., et al. 2023, PASP, 135, 048003 [NASA ADS] [CrossRef] [Google Scholar]
  141. Xie, Y., & Ho, L. C. 2019, ApJ, 884, 136 [CrossRef] [Google Scholar]

All Tables

Table 1.

Properties of the robust qPAH sample (Section 2.2). Table contains: source ID from SMILES internal v0.3 catalog, redshift, PAH fraction and error, stellar mass and error in M⊙, metallicity (12 + log(O/H)) and error calculated from the fundamental metallicity relation (FMR; as plotted in Figures 8 and 9) and from the mass metallicity relation (MZR; as plotted in Figure 7).

In the text
Table 2.

Best-fit parameters of fobscured − M* for the full sample in Equation (3).

In the text
Table 3.

Fit parameters of the linear fits in Figure 12.

In the text

All Figures

thumbnail Fig. 1.

Power of SMILES in studying the mid-IR dust properties of galaxies at cosmic noon. Left: The top-left image shows a group of galaxies at z ∼ 0.7 − 2.3 (matching the redshift range in this paper) in F444W/F200W/F090W NIRCam colours (JADES). The pre-JWST mid-IR view of these galaxies is shown in the top row from Spitzer IRAC and MIPS (GOODS survey; Dickinson & FIDEL Team 2007; Ashby et al. 2015). The bottom two rows show the mid-IR images with JWST MIRI at 5.6, 7.7, 10, 12.8, 15, 18, 21, and 25.5 μm (SMILES). The PSF sizes are shown with white circles in the corners (diameter of the circle is the FWHM). The unprecedented improvement of MIRI in spatial resolution (0.19 to 0.86″ from 5.6 to 25.5 μm) compared to that of IRAC (1.72 and 1.88″ at 5.8 and 8 μm) and MIPS 24 μm (6″) makes it possible to observe the mid-IR emission of individual typical galaxies at these redshifts. Right: The IR dust SEDs of typical galaxies at z = 1.8 with IR luminosities of 1010.5 − 1011.5 L⊙ (Rieke et al. 2009; corresponding to obscured SFRs of ∼5 − 50 M⊙/yr assuming the Kennicutt & Evans 2012 calibration) in grey shaded region, along with 3σ sensitivity limits of the GOODS-S Herschel/PACS (green; Magnelli et al. 2013), Spitzer/MIPS 24 μm confusion limit (red; 56 μJy, Dole et al. 2004), Spitzer IRAC Channels 3 and 4 (blue; Guo et al. 2013), and the MIRI sensitivities of SMILES in ∼10 − 30 min exposures (orange; Section 2.1). MIRI filter transmission curves are shown with orange shaded regions. The high sensitivity and multi-band capability of MIRI enables measurements and characterisations of IR emission of typical galaxies at cosmic noon.
In the text
thumbnail Fig. 2.

Left panel: SFR versus stellar mass of the sample. The sample is divided into those with robust and low-confidence PAH mass fractions (same as in Figure 3). The shaded region indicates star-forming main sequence at the redshift range of our galaxies, z = 0.7 − 2.0, derived from the PROSPECTOR-inferred SFR and mass of Leja et al. (2022), same as the SFR and stellar masses inferred in this work. Three SED examples of the symbols with red edges are shown on the right. Right panel: Examples of the SEDs of three galaxies that are above, on, and below the main sequence, shown with the red edges in the left plot. The MIRI filter transmission curves are also shown. The wealth of data from HST, NIRCam, and MIRI provides robust SED fits for this sample at z = 0.7 to 2.0. More examples of the SED fits are provided in the online repository: https://zenodo.org/records/12671075.
In the text
thumbnail Fig. 3.

Distributions of redshift (left), F444W flux density (middle), and F1500W flux density (right) for the full sample (N = 443) and the sub-sample with robust PAH mass fractions (N = 216) defined as those with qPAH error < 0.5% or qPAH parameter constrained by > 3σ from the SED fitting (Section 2.2). The sample is purely star-forming with AGN and quiescent galaxies removed (Section 2.2).
In the text
thumbnail Fig. 4.

Ratio of the PAH-to-dust mass fraction to the PAH-to-total IR luminosity fraction versus the PAH mass fraction in our sample. Both quantities are derived from the Draine & Li (2007) models (Section 2.3). Robust qPAH sample shows galaxies with qPAH with > 3σ significance or less than 0.5% error (Section 2.2). Left: PAH luminosity fraction is defined as the ratio of the PAH 7.7 μm feature luminosity to total IR luminosity. Horizontal line is the unity line. The robust sample is fit with a polynomial function shown with a dashed curve (Equation (1)). Right: PAH luminosity is the sum of the 3.3, 6.2, 7.7, 11.2, and 17 μm PAH features luminosities (Section 2.3.1). Horizontal line shows the median of the robust sample (0.68). We note that qPAH is not in percentage units, unlike the other figures in this paper.
In the text
thumbnail Fig. 5.

Left panel: PAH-to-dust mass fraction (qPAH) versus 15 μm (F1500W) to 25.5 μm (F2550W) flux ratios for a sample of z = 0.7 − 0.9 galaxies with significant (> 3σ) detections in F1500W and F2550W. qPAH is derived from PROSPECTOR (the Draine & Li 2007 models), while the flux ratio is an empirical tracer of PAH to warm dust emission, as is shown in the right panel. The significant linear correlation of the two quantities (Pearson correlation coefficient of 0.71 with p-value = 0.001) indicates the validity of the estimated qPAH values. Right panel: Two mid-IR spectra with a high PAH fraction (solid) and low PAH fraction (dashed), overlaid with the wavelength coverage of the F1500W and F2550W filters at z = 0.7 − 0.9. In this redshift range, F1500W and F2550W filters trace the PAH dominated and non-PAH-dominated dust emission in star-forming galaxies, respectively. Therefore, their ratio is expected to correlate with PAH fraction.
In the text
thumbnail Fig. 6.

PAH to total dust mass fraction for the 38 galaxies with ALMA 1.1 mm detection (from the ASPECS survey; Walter et al. 2016). Five of them also have 3 mm detections. The axes show the derived qPAH including and excluding the ALMA data points. Median of the qPAH values without ALMA to those with ALMA data is 0.95, completely within the qPAH uncertainty, indicating the qPAH values inferred based on UV-to-MIRI data alone are robust.
In the text
thumbnail Fig. 7.

PAH mass fraction (left) and luminosity fraction (right) as a function of stellar mass. Moving median (black curve) is shown for the robust qPAH sample (see Section 2.2 for the definition of samples), and all galaxies are colour-coded by sSFR. In the left panel, horizontal lines show the median PAH mass fractions of z ∼ 0 galaxies with 12 + log(O/H) < 8.1 and > 8.1 from Draine et al. (2007). On the top x-axes, we also show the estimated metallicities from the O3N2-based mass-metallicity relation (MZR) of Topping et al. (2021) at z ∼ 1.5, and assuming the Pettini & Pagel (2004) calibration. The z ∼ 0.7 − 2 sample has a very similar qPAH-metallicity behaviour to that inferred at z ∼ 0. Properties of the robust sample are in Table 1.
In the text
thumbnail Fig. 8.

PAH mass fraction versus metallicity. Metallicity was derived from the FMR of Sanders et al. (2021). The robust and low-confidence qPAH samples (Section 2.2) are shown with larger and smaller circles, respectively. We provide the values of the robust sample in Table 1. The z ∼ 0 data from Aniano et al. (2020) are shown in red. Following the analysis of Aniano et al. (2020), we fit both samples with a linear function, shown with solid lines (slopes of 3.63 ± 0.71 and 4.04 ± 0.51 and intercepts of −28.60 ± 6.14 and −31.94 ± 4.38 for the z ∼ 0 and 1.3 sample, respectively). The medians of the two samples below and above 12 + log(O/H) = 8.25 (dotted lines) are also shown. The two samples follow very similar trends. The average scatter in 12 + log(O/H) from FMR (0.05 dex, see text) and the strong-line metallicity calibration uncertainty for the z ∼ 0 sample (0.2 dex; Aniano et al. 2020) are shown in the bottom right. The error bars on the z ∼ 1.3 data are the metallicity measurement uncertainties from the SFR and mass uncertainties. The linear fits (solid lines) have slopes of 3.6 and 3.4 for the z ∼ 0 and 1.3 samples, respectively.
In the text
thumbnail Fig. 9.

PAH mass fraction as a function of metallicity at z ∼ 1.3 (this work) and z ∼ 0 (Aniano et al. 2020; Rémy-Ruyer et al. 2015). Here, we only include the robust qPAH sample at z ∼ 0.7 − 2.0. Top: The z ∼ 1.3 data presented in this work is shown with orange circles. The orange line shows the moving median. Metallicity of the z ∼ 1.3 sample is estimated using the FMR relation of Sanders et al. (2021). The z ∼ 0 data is shown for the PP04 metallicity calibrations of Aniano et al. (2020) (purple diamonds, and purple line for the moving median) and the PT metallicity calibrations of Aniano et al. (2020) and Rémy-Ruyer et al. (2015) (green squares, and the green line for the moving median). The Rémy-Ruyer et al. (2015) data extend the z ∼ 0 sample to much lower metallicities. The two metallicity calibrations are systematically different (on average ∼0.2 dex but can be up to 0.4 dex); therefore, we show both for completeness. Bottom: Three-step fits (constant+linear+constant) to the moving median trends in the top panel. The shaded regions show the error in the mean in each consecutive bin of the moving median. Despite the uncertainties in metallicities, the overall qPAH-metallicity behaviour of the z ∼ 0 and z ∼ 1.3 samples are similar within the scatter.
In the text
thumbnail Fig. 10.

PAH mass fraction as a function of galaxy parameters. From top-left to bottom-right: age of the galaxy, SFR, stellar mass, obscured luminosity fraction, SFR surface density (using F1500W sizes). The robust sample is shown with a teal colour and the low-confidence sample with smaller grey symbols (see Section 2.2 for sample definitions). The moving medians of the full (robust+low-confidence) and robust samples are shown as grey and black curves, respectively. In the bottom row, the unresolved sources in F1500W images are shown with triangles as lower limits on SFR surface density. Among the parameters show, qPAH has the strongest correlations with mass, age, and obscured luminosity fraction.
In the text
thumbnail Fig. 11.

Obscured luminosity fraction as a function of stellar mass for the full sample (left) and separated by redshift (right). Obscured fraction is defined as the obscured UV to total (intrinsic) UV luminosity at 1550 Å, inferred from the best-fit UV-to-IR SEDs. We show the moving median (dashed thick lines), moving weighted-average (dotted line) and best-fit curve (solid lines) to the samples at M* > 4 × 108 M⊙, where the data is mass-complete. In the left panel, we also show the Whitaker et al. (2017) fit to z = 0.5 − 2.5 with an orange curve. The Whitaker et al. (2017) study was based on Spitzer/MIPS data with a wider area but biased to more obscured systems. Our weighted-average trend is also dominated by the heavily obscured systems, and therefore similar to the (Whitaker et al. 2017) curve. However, the median trend that is more representative of the full population captured by the deeper MIRI data (relative to the MIPS data) is systematically lower. Furthermore, as is shown in the right panel, there is no redshift evolution in this relation in our sample.
In the text
thumbnail Fig. 12.

Obscured luminosity fraction as a function of ΣSFR (using F1500W sizes) and F1500W effective radius (middle) for the F1500W spatially resolved sample (the filter FWHM is 0.5 arcsec). At a given mass, fobsc increases with ΣSFR and decreases with rest-frame mid-IR (dust) radii. Right panel shows SFR versus F1500W size for the same sample. The near constant SFR with Re, F1500W in each mass bin indicates that the relationship between fobsc and size is independent of SFR. Individual measurements are shown with small symbols and colour-coded in three stellar mass bins with the same number of galaxies, shown in the legend. In each mass bin, average values in bins of the parameter on the x axis are shown with larger symbols with the corresponding shape and colour of the mass bin. Pearson correlation coefficients (ρ) are shown in the corners of the plots with corresponding colours of each mass bin. Linear fits to the average values of fobsc versus log(ΣSFR) are shown in the left panel. The fit parameters are in Table 3.
In the text
thumbnail Fig. 13.

Cartoon illustrating a physical explanation of the correlation between fobsc and star-forming compactness. Stars are shown in blue. Diffuse ISM dust is shown with light red and the ‘birth cloud’ dust with higher column density is shown with a darker red colour. Schematically, less and more dust-obscured light (i.e. obscured by the low and high column density dust, respectively) are shown with blue and red arrows, respectively, reaching to the observer on the right. Extended galaxies have a range of dust-star geometries, while compact galaxies contain most of their stellar population in the core with high dust covering fraction, resulting in most of the emitted starlight being obscured by dust.
In the text
thumbnail Fig. 14.

IRX (ratio of IR to UV 1550 Å luminosity) as a function of stellar mass (left panel) and UV stellar continuum slope (middle panel). Galaxies with spatially resolved morphology in F1500W are colour-coded by their ΣSFR. A linear fit to log(IRX)−log(M*/M⊙) is shown in the left panel (slope of 0.96 ± 0.06 and intercept of −8.47 ± 0.61). In the middle panel, we show three IRX-β relations in the literature adopted from Reddy et al. (2018) assuming a constant star formation history and an age of 100 Myr for stellar populations: the original Meurer et al. (1999) relation, the starburst curve of Calzetti et al. (2000) and the SMC curve of Gordon et al. (2003) assuming 0.14 Solar metallicity. A higher metallicity system will result in a redder intrinsic UV slope (β0), shifting the curves to the right of the diagram (e.g. the Calzetti curve for a 1.4 Z⊙ population and β0 = −2.4 resembles the Meurer et al. 1999 curve). Galaxies with higher ΣSFR at a given mass or β have higher IRX and a shallower attenuation curve. Right panel: V-band dust optical depth versus ΣSFR, colour-coded with the attenuation curve slope defined as the deviation from the Calzetti et al. (2000) (the formalism of Kriek & Conroy 2013), where zero is the Calzetti curve slope. The two parameters are highly correlated with ρ = 0.65 (p-value ≪ 1). The shallower attenuation curve of galaxies with high IRX at a given mass or β can be explained by the radiative transfer effects that are a result of their high ΣSFR: higher optical depths and lower fractions of unobscured evolved stars.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

OSZAR »