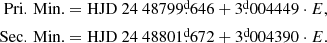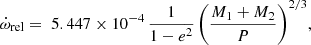| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A231 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450303 | |
| Published online | 10 October 2024 | |
Apsidal motion and TESS light curves of three southern close eccentric eclipsing binaries: GM Nor, V397 Pup, and PT Vel⋆
1
Astronomical Institute, Faculty of Mathematics and Physics, Charles University Prague, V Holešovičkách 2, CZ-180 00 Praha 8, Czech Republic
2
Institute of Theoretical Physics and Astrophysics, Masaryk University, Kotlářská 2, CZ-611 37 Brno, Czech Republic
3
FZU – Institute of Physics of the Czech Academy of Sciences, Na Slovance 1999/2, CZ-182 21 Praha 8, Czech Republic
4
Czech Astronomical Society, Variable Star and Exoplanet Section, Vídeňská 1056, CZ-142 00 Praha 4, Czech Republic
5
Observatory and planetarium Hradec Králové, Zámeček 456, CZ-500 08 Hradec Králové, Czech Republic
6
Private Observatory, CZ-683 41 Pavlovice 65, Czech Republic
7
Private Observatory, Plumstead, Cape Town, South Africa
Received:
9
April
2024
Accepted:
7
August
2024
The study of apsidal motion in eccentric eclipsing binaries provides an important observational test of theoretical models of stellar structure and evolution. New ground-based and space-based photometric data have been obtained and archival spectroscopic measurements were used in this study of three detached early-type and southern-hemisphere eccentric eclipsing binaries GM Nor (P = 1d.88, e = 0.05), V397 Pup (3d.00, 0.30), and PT Vel (1d.80, 0.12). Their TESS observations in several sectors have also been included and the corresponding light curves were solved using the PHOEBE code. As a result, new accurate photoelectric times of minimum light have been obtained. The newly completed O − C diagrams were analyzed using all reliable timings found in the literature and calculated using the TESS light curves. New or improved values for the elements of apsidal motion were obtained. Using ESO archive spectroscopy, for V397 Pup, the precise absolute parameters were newly derived: M1 = 3.076(35) M⊙, M2 = 2.306(35) M⊙, and R1 = 2.711(55) R⊙, R2 = 1.680(55) R⊙. For PT Vel the absolute dimensions were improved: M1 = 2.204(25) M⊙, M2 = 1.638(25) M⊙, and R1 = 2.108(30) R⊙, R2 = 1.605(30) R⊙. For GM Nor, the less accurate absolute parameters based on the light curve analysis were evaluated: M1 = 1.94(15) M⊙, M2 = 1.84(14) M⊙, and R1 = 2.27(20) R⊙, R2 = 2.25(20) R⊙. We found more precise and relatively short periods of apsidal motion of about 80, 335, and 160 years, along with the corresponding internal structure constants, log k2, –2.524, –2.361, and –2.563, for GM Nor, V397 Pup, and PT Vel, respectively. Relativistic effects are small but not negligible, making up to 10% of the total apsidal motion rate in all systems. No marks of the presence of the third body were revealed in the light curves, on the O − C diagrams, or in the reduced spectra of the eccentric systems studied here.
Key words: binaries: eclipsing / stars: early-type / stars: fundamental parameters / stars: individual: GM Nor / stars: individual: V397 Pup / stars: individual: PT Vel
Based on observations secured at the South Africa Astronomical Observatory, Sutherland, South Africa, Mt. John University Observatory, University of Canterbury, Lake Tekapo, New Zealand, SPACE Atacama Lodge, San Pedro de Atacama, Chile, and FRAM, Pierre Auger Observatory, Argentina.
Corresponding author; [email protected]
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Eccentric eclipsing binaries (EEBs) provide an ideal opportunity for studying the stellar structure of the stars as well as testing general relativity effects outside of the Solar System. The Newtonian contribution to the observed apsidal motion in such systems is highly dependent on stellar radii (r−5). Therefore, only systems with accurate determinations of their absolute dimensions and precise apsidal motion periods can be used to test current stellar structure models (Claret & Giménez 2010; Claret & Torres 2019). A precise determination of the apsidal motion rate requires long-term monitoring of mid-eclipse times, usually spanning several decades, and many advanced amateur observers can help with this difficult task. Moreover, detached double-lined eclipsing binaries (DLEBs) simultaneously serve an important source of fundamental information on stellar masses and radii (Andersen 1991). Torres et al. (2010) revised the absolute dimensions of 94 DLEBs and only 18 of them are found to have eccentric orbits and show apsidal motion suitable for the apsidal motion test of the stellar structure.
An analysis of apsidal motion in eclipsing binaries using TESS data was presented by Baroch et al. (2021, 2022). These authors determined the apsidal motion rate for nine EEBs, measured the general relativistic apsidal motion rate, and carried out a test of general relativity. They found a perfect agreement with theoretical predictions and established stringent constraints on the parameters of the post-Newtonian formalism. Recently, Claret et al. (2021) studied the internal structure constant in 34 EEBs and nearly doubled the sample of suitable systems collected by Torres et al. (2010). Their comparison of the apsidal motion rate with predictions based on new theoretical models shows a very good agreement. Clearly, it is necessary to expand the current collection of EEBs with precise absolute parameters to provide better statistics on these results.
Here, we analyze the available observational data and apsidal motion rates for three detached eclipsing systems. All these systems are relatively neglected bright southern-hemisphere objects of a similar spectral type that are known to have eccentric orbits and to exhibit relatively rapid apsidal motion. Their orbital periods are between 2 and 3 days. With the exception of PT Vel, no radial velocities have been published for any of these binary systems. V397 Pup and PT Vel were also included in the new Catalog of TESS eclipsing binary stars collected by Prša et al. (2022). Their basic properties are summarized in Table 1. The previous O − C diagrams for these systems can also be found in the O − C gateway1.
Basic properties of selected eclipsing binaries.
This study of apsidal motion in EEBs is a continuation of our work presented in earlier papers over several years (Wolf et al. 2008, 2019, 2022). The current paper is organized as follows. Section 2 deals with new observations and data reductions. The apsidal motion analysis is given in Sect. 3, while the light curves and the radial velocity curves are analyzed in Sect. 4. The internal structure constants are derived in Sect. 5 and a brief summary of the results presented is given in Sect. 6.
The detached eclipsing binary GM Nor (also CD −54° 6427, CPD −54° 6718, FL 1816, TIC 81569380; Vmax = 10m.6, Sp. A3V) is a relatively poorly studied binary with a known and relatively fast apsidal motion. It was discovered to be a variable star by Kruytbosch (1932) and later Plaut (1946) derived the first light elements; Savedoff (1951) included GM Nor in the list of eclipsing binaries with the displayed secondary eclipse. Soderhjelm (1975) obtained precise UBV photometry using the 50-cm telescope at La Silla, Chile, and found an apsidal motion with a period of about 90 ± 15 years. The following light ephemeris were presented in the last-mentioned paper:
Subsequently, GM Nor was included in several catalogs of eccentric orbit eclipsing binaries (Malkov et al. 2006; Bulut & Demircan 2007; Avvakumova et al. 2013; Kim et al. 2018). For GM Nor, the angular diameter of the system ρ = 0.047 mas was also measured by the Gaia satellite and this value is included in the Mid-infrared stellar Diameters and Fluxes compilation Catalogue (Cruzalèbes et al. 2019, MDFC ver. 10).
To our knowledge, no radial velocity data have been published for this interesting and relatively bright system and almost 50 years have elapsed since the last published photometric study from Soderhjelm (1975). Surprisingly, no study that is directly focused on GM Nor has been found in the literature. Furthermore, there is no spectrum of GM Nor in the ESO Archive obtained in the past.
The detached eclipsing binary V397 Pup (also HD 63786, HIP 38167, CD −34° 3970, CPD −34° 1717, TIC 150284425; Vmax = 5m.93, Sp. B9V) is a relatively newly discovered bright early-type binary with a significant eccentricity of e ≃ 0.3 and a short orbital period of about 3.0 days. It is a known visual binary system that was first suspected to be a variable star (BV 438) by Strohmeier et al. (1964). V397 Pup was discovered to be an EEB by Otero (2005) using the HIPPARCOS and ASAS-3 photometry database. Otero also reported a relatively fast apsidal motion and derived the following light ephemeris:
With a period in days that is almost precisely an integer number, V397 Pup is a rather difficult object to study from only one observatory. Recently, V397 Pup was included in a new catalog of pulsating stars detected in EA-type eclipsing binaries based on TESS data (Shi et al. 2022). To our knowledge, precise radial-velocity observations of this system have not been published so far. We used 28 spectrograms of V397 Pup found in the ESO Archive and obtained in different projects during 2009 – 2021, see Table B1. The TESS light curve is also solved in the TESS eclipsing binary catalog2, where an effective temperature, Teff = 10 666 K, was given.
The first photometric observations of V397 Pup were made by the HIPPARCOS mission and 138 points were collected, covering an interval of 3.2 years. Unfortunately, only a few data points covering the eclipse phases are available. This is particularly true for the secondary eclipse phase.
The detached eclipsing binary PT Velorum (also HD 79154, CD−42° 5038, HIP 45079, BV 469, TIC 74528791, NSV 04409; Vmax = 7m.03; Sp. A0V) was a relatively little known early-type binary with a moderate eccentric orbit (e = 0.13) and a short orbital period of about 1.8 days. It was discovered to be a variable by Strohmeier et al. (1964) on photographic plates taken in Johannesburg. Its eclipsing nature was revealed by HIPPARCOS (Perryman 1997) and Otero (2003) later found that the system exhibits an apsidal motion. Using high-resolution echelle spectra, Bakış et al. (2008) derived the absolute dimensions of the components and presented the following linear light elements:
These authors confirmed a significant orbital eccentricity of e = 0.127 ± 0.006 and a short period of apsidal motion of U = 182.2 ± 8.4 year. We also refer to the series of cited works published on this binary described in that paper. Using the TESS data, Claret et al. (2021) recalculated the apsidal motion and the internal stellar structure of the system. The TESS light curve is also solved in the TESS eclipsing binary catalog, where the effective temperature Teff = 10 239 K is given. Recently, PT Vel was included in the BANANA project (Marcussen & Albrecht 2022), the study of spin-orbit alignment in close binaries.
2. Observations
2.1. Ground-based photometry
Our new photoelectric observations were obtained at several different southern observatories in the past, in chronological order:
-
Mt. John University Observatory (MJUO), University of Canterbury, Lake Tekapo, New Zealand: 0.61-m Cassegrain reflector (f/16) equipped with a single-channel photon-counting photometer (utilizing an EMI 9202B photomultiplier) and Johnson UBV filters or a SBIG ST-9 CCD camera with BVR filters; covers over two weeks in January 2007.
-
South African Astronomical Observatory (hereafer SAAO), Sutherland, South Africa: the 0.50-m Cassegrain reflector (f/18) equipped with a modular photometer utilizing a Hamamatsu EA1516 photomultiplier and Johnson UBV filters or an objective Helios 2/58 with an ATIK 16 IC CCD camera; during two weeks in November 2008 and April 2010. The objective Helios 2/58 with a camera G2-402 (BVR filters) was used in March 2018.
-
SPACE Atacama Lodge, San Pedro de Atacama (SPA), Chile: 0.20-m reflector (f/4) with a SBIG ST-8 CCD camera and VR filters; during two weeks in April 2010.
-
Fotometric Robotic Atmospheric Monitor (Ebr et al. 2014, FRAM), Pierre Auger Observatory, Argentina: 0.30-m reflector with a G2-1600 CCD camera and BVRI filters; during two epochs in October 2013 and June 2014.
-
Private observatory of S.N. de Villiers in Plumstead, Cape Town, South Africa: Celestron 280/1764 telescope, a SBIG ST-8XME CCD camera, and BVRI filters during 13 nights in the 2019–2020 season.
The main aim of these photometric measurements was to obtain the whole light curve or at least to secure several well-covered primary and secondary eclipses for all variables. Due to the limited observation time, complete light curves were obtained only for GM Nor. Each observation of an eclipsing binary was accompanied by the observation of a local comparison and check stars (see Table 2). We note that in the neighborhood of PT Vel there is also a bright δ-Sct variable star MP Vel (V = 7.8 mag) which is not suitable as a comparison.
Selected local comparison and check stars at different observatories.
Photoelectric measurements at MJUO and SAAO were usually performed using Johnson’s UBV photometric filters with a 10-second integration time. All observations were carefully reduced to the Cousins E region standard system (Menzies et al. 1989) and corrected for differential extinction using the reduction program HEC 22 rel. 16 (Harmanec & Horn 1998). The standard errors of the UBV measurements at SAAO were approximately 0.009, 0.007 and 0.006 mag in the U, B and V filters, respectively. The software package C-MUNIPACK3 for aperture photometry, based on the DAOPHOT procedure, was used to process the set of CCD frames. Examples of our photometric observations of GM Nor obtained at SPA and Cape Town observatories are given in Fig. 1.
 |
Fig. 1. Examples of our observations. Upper panel: observed differential V light curve of GM Nor obtained at SPA observatory (blue dots) in April 2010. Lower panel: observed VRI light curves of GM Nor obtained at Cape Town in 2020. The PHOEBE solutions are plotted as black curves. |
2.2. TESS photometry
Moreover, the Transiting Exoplanet Survey Satellite (TESS) mission to study exoplanets through photometric transits (Ricker et al. 2015), with its nearly full sky coverage, also provides precise photometry of a large sample of eclipsing binary systems with a time baseline of 27 days to several years. Thus, precise monitoring of light curves is possible from space and their exceptional quality is perfect for studying light curves and eclipse timings (Baroch et al. 2021). The three systems studied in this work have been observed by TESS in several sectors (see Table 3). For GM Nor and PT Vel, we collected simple aperture photometry (SAP) of available cadence produced by the Science Process Operation Centre (SPOC) (Jenkins et al. 2016) available at Mikulski Archive for Space Telescope (MAST)4. In the case of V397 Pup, the original FFI data from the TESS archive were downloaded and reduced using the Lightkurve code5 in the standard procedure.
TESS visibility and sectors used for light curve analyses and for mid-eclipse time determination.
The new times of primary and secondary minima and their errors were determined using a least-squares fit of the light curve during eclipses. Three or fourth-order polynomial fittings were applied to the bottom sections of the light curves. The mean values of the individual filter bands are given and the presented errors represent the fitting mean error for each light curve. For the TESS data, the mid-eclipse times were determined by SILICUPS6 code.
Because the TESS data are provided in the Barycentric Julian Date Dynamical Time (BJDTDB), all our previous times were first transformed to this time scale using the often used Time Utilities of Ohio State University7 (Eastman et al. 2010).
2.3. Hipparcos, ASAS-3, and OMC photometry
Using the HIPPARCOS photometry (Perryman 1997), taken from the Epoch Photometry Annex, All Sky Automated Survey-3 (ASAS-3) database8 (Pojmanski 2002), and photometric data from the OMC INTEGRAL Optical Monitoring Camera Archive (Mas-Hesse et al. 2004)9 we were able to derive several additional times of minimum light with a lower precision. They were used in our next analysis with lower weight.
To derive some of the eclipse times from various photometric surveys, we used the following approach. Due to having only sparse photometry (i.e., typically a few data points per night only), we used our method named AFP (described in our paper Zasche et al. (2014)). It uses the phased light curve over a longer time interval and the template of the light curve provided through light curve modeling in PHOEBE. The time interval used was typically one year, but this can be arbitrarily changed with respect to the number of data points in each interval. We are typically able to derive several times of eclipses, primary and secondary, using this method from one particular photometric survey dataset.
All new minima times are included in Tables A1–A5. In these tables, the epochs are calculated from the light ephemeris given in the text. The other columns are self-evident.
2.4. Spectroscopy
The only system in this study with previously published spectroscopy and a radial velocity curve is PT Vel (Bakış et al. 2008). A total of 28 radial velocities obtained using the HERCULES spectrograph at Mount John University Observatory, Lake Tekapo, New Zealand, in May 2006, are available.
The ESO HARPS – High Accuracy Radial velocity Planet Searcher10 (Mayor et al. 2003) and FEROS – Fiber-fed Extended Range Optical Spectrograph11 have been used in several projects for spectroscopy of our objects in the past12. We retrieved the publicly available HARPS spectroscopic data sets from the ESO Science data archive13. For V397 Pup we found 28 original spectra in the Archive, for PT Vel there were additional 16 spectra at our disposal. All spectra were reduced in the standard way using IRAF14 routines. The spectra were bias-corrected and flat-fielded. From the archival spectra, the absorption lines of prominent Balmer lines of Hα, Hβ, or Hγ were detected. Unfortunately, the broad hydrogen lines exceeded the aperture size, so the more suitable Mg4481 and Fe5018 lines were used to measure the radial velocities (see Fig. 2 and Tables B1 and B2). The Gaussian fit with the IRAF program was used to determine individual radial velocities. To our knowledge, for a relatively bright target GM Nor, no spectroscopic material or radial velocities have been reported in the literature or found in any electronic database.
 |
Fig. 2. Sample of 20 HARPS spectra of V397 Pup with prominent He4471 and Mg4481 absorption lines. |
3. Apsidal motion analysis
Precise determination of the apsidal motion requires long-term monitoring of eclipse times, usually spanning several decades. As usual, the apsidal motion in EEBs can be studied using an O − C diagram (ETV curve) analysis. As in our previous studies, the iterative method described by Giménez & Garcia-Pelayo (1983) or Giménez & Bastero (1995) was used routinely. We collected all reliable times of minimum light available in the literature and current databases. The input files of the mid-eclipse times were supplemented with our own measurements and numerous data from TESS. We computed all TESS mid-eclipse times from the whole available light curves. All modern photoelectric and CCD times, as well as TESS minima were used with a weight of 10 in our calculation. Previous, less accurate measurements with unknown uncertainty (photographic or visual estimations) were assigned weights of 3, 1, or 0.
Apsidal motion parameters were calculated iteratively. For the orbital inclination, we adopted the results from our own photometric solution (see Section 4 and Table 4). For the eccentricity, we adopted the value from the apsidal motion analysis. In general, the apsidal motion solution was found to be insensitive to relatively large changes in inclination but strongly depends on the orbital eccentricity.
Parameters of the fit to the TESS light curve for GM Nor, V397 Pup and PT Vel.
In case of GM Nor, all photoelectric times of minimum light given in Plaut (1946) and Soderhjelm (1975, his Table 7) were incorporated into our calculation. Our new VR CCD photometry obtained at the SPA (1590 measurements in both filters) and Cape Town observatories (see Fig. 1) was used for the determination of new mid-eclipse times. Several times with less precision were derived using ASAS and OMC photometry. A large number of very precise and consecutive times were obtained using the TESS data in three sectors. A total of 165 times of minimum light were used in our analysis, with 82 secondary eclipses among them. All are listed in Tables A1 and A2.
The calculated parameters of the apsidal motion and their internal errors of the least-squares fit (in brackets) are given in Table 5. In this table, Ps denotes the sidereal period, Pa the anomalistic period, e represents the eccentricity, and  is the rate of advance of the periastron (in degrees per cycle or in degrees per year). The zero epoch is given by T0, and the corresponding position of the periastron is represented by ω0. The orbital eccentricity was taken as a free parameter in our calculations and was used for the light-curve solution (see Section 4). The resulting values of e have lower intrinsic errors compared to those determined independently from the light curve analysis. This procedure usually gives us a better result for this important element. The O − C diagram is shown in Fig. 3.
is the rate of advance of the periastron (in degrees per cycle or in degrees per year). The zero epoch is given by T0, and the corresponding position of the periastron is represented by ω0. The orbital eccentricity was taken as a free parameter in our calculations and was used for the light-curve solution (see Section 4). The resulting values of e have lower intrinsic errors compared to those determined independently from the light curve analysis. This procedure usually gives us a better result for this important element. The O − C diagram is shown in Fig. 3.
Apsidal motion elements of GM Nor, V397 Pup, and PT Vel.
 |
Fig. 3. Historical O − C diagram of GM Nor together with our best-fit apsidal motion model. The blue solid curve and green circles correspond to the primary, the orange curve and yellow triangles to the secondary minima. Larger symbols denote the photoelectric or CCD measurements which were given higher weights in the calculations. The O − C2 residuals are plotted in the bottom panel. |
For V397 Pup, all times of minimum light given in (Otero 2005, his Table 2), our new timings derived from the HIPPARCOS database, the results of our new measurements at SAAO observatory, as well as numerous TESS eclipse times were included in our analysis. The epochs in Table A3 were calculated according to the basic minimum given in the HIPPARCOS catalog. A total of 78 times of minimum light were used in our analysis, with 35 secondary eclipses among them. The calculated parameters of the apsidal motion and their internal errors of least squares fit are given in Table 5. The current O − C diagram is shown in Fig. 4.
 |
Fig. 4. O−C diagram for V397 Pup. See legend to Fig. 3. Although primary minima fit the curve well, the secondary have a larger scatter. Minima derived from TESS sectors are bulks of points close to epoch 3400, 3600 and 3800. |
In case of PT Vel, all mid-eclipse times given in (Otero 2003, his Table 2) were incorporated into our analysis. Seven new and precise times were derived using our SAAO and MJUO observations. Additional timings derived from the HIP photometry (135 points spanning an interval of about three years), ASAS and INTEGRAL OMC camera were included. The usefulness of the HIPPARCOS data is partially limited by the lack of observations during the secondary minimum. The fully covered and rather scattered V light curve is available in the ASAS-3 Photometric Catalogue. The most numerous contribution of minima comes from five TESS sectors. The newly determined times of minimum light are listed in Tables A4 and A5, where all epochs were computed according to the ephemeris given in Bakış et al. (2008). In our analysis, a total of 154 times of minimum light were used. The residuals of O − C values for all minimum times with respect to the linear part of the apsidal motion equation are shown in Fig. 5. The computed elements of apsidal motion and their internal errors of least squares fit are given in Table 5. The nonlinear predictions, corresponding to the fitted parameters, are plotted as blue and orange curves for primary and secondary eclipses, respectively.
 |
Fig. 5. Current O − C diagram for PT Vel. See legend to Fig. 3. Numerous minima derived from TESS sectors are groups of points close to epoch 5700, 6100, and 6500. |
4. Light curve and radial velocities analysis
Due to the relatively lower quality data obtained at the MJUO, SAAO, SPA, FRAM, and Cape Town observatories compared to the TESS data, only the TESS light curves were selected to fit the light curves of three systems. The completely covered light curves were routinely analyzed using the PHOEBE computer code, version 31c, developed by Prša & Zwitter (2005), see also Prša (2018), which is a user-friendly implementation of the well-known Wilson-Devinney code (Wilson & Devinney 1971). To reduce the long computation time for eccentric binaries, the TESS light curves were phased-binned to 300 points each. The other photometric data available to us were used mostly for mid-eclipse time determination and solution of apsidal motion.
The light elements and the apsidal motion parameters (eccentricity, position of the periastron, and apsidal motion rate) have been adopted from the apsidal motion analysis (see Sect. 3 and Table 5) because the minima times cover a longer time span and these quantities are derived with higher precision. The other light curve parameters have been fitted: the luminosities, temperature of the secondary, inclination, and Kopal’s modified potentials. The temperature of the primary component was adopted as a mean value of several sources or fixed in agreement with previous investigators (see Table 6).
Temperatures of selected binaries found in different sources.
The fitting of the F1, F2 synchronicity parameters in PHOEBE was unstable. During the procedure, their resulting values oscillated between 0.8 and 2.0. Thus, we assumed the synchronous rotation for both components (F1 = F2 = 1). Moreover, in the case of elliptical orbits, the rotation tends to synchronize because of tidal interactions between the two components. The limb-darkening coefficients were interpolated from van Hamme’s tables (van Hamme 1993), using the linear cosine law. The fine and coarse grid rasters for both components were set at 30. Numerous PHOEBE runs were evaluated in detached mode using a different configuration of initial parameters. The results and the value of the cost function were recorded. The final solution was accepted when subsequent iterations did not result in a decrease of the PHOEBE cost function.
The results of the photometric analysis are given in Table 4. In this table, T1, T2 denote the temperatures of the primary and secondary components, r1, r2 the relative radii, and i the orbital inclination. The corresponding light curves are plotted in Figs. 6, 7 and 8, respectively. The TESS phased-binned light curve of V397 Pup shows asymmetric maxima (Fig. 7). These out-of-eclipse variations are caused by the effect of light reflection from one component to the other and are well resolved using the PHOEBE code.
 |
Fig. 6. TESS light curve of GM Nor obtained in Sector 12 (May/June 2019, orange circles) and its PHOEBE solution (black curve). The residuals from the solution are plotted in the bottom panel. |
 |
Fig. 7. Solution of light and radial velocity curves for V397 Pup. Upper panel: TESS light curve (orange circles, binning 300) and its PHOEBE solution (black curve). Lower panel: radial velocity curve of V397 Pup and its PHOEBE solution (primary component in orange, secondary in blue). The residuals of the solution are plotted in the bottom panels. |
 |
Fig. 8. Solution of light and radial velocity curves for PT Vel. Upper panel: TESS light curve (orange circles, binning 300) and its PHOEBE solution (black curve). Lower panel: Radial velocity curve of PT Vel obtained by Bakış et al. (2008) and new data, and its PHOEBE solution. Primary component in blue, secondary component in orange. The residuals of the solution are plotted in the bottom panels. |
The results of the radial velocity analysis and absolute dimensions are listed in Table 7. For GM Nor, the dimensions were estimated using the PHOEBE solution and the spectral type and were interpolated in the table of Pecaut & Mamajek (2013)15.
Astrophysical parameters and internal structure constants.
5. Internal structure constant
Observations of binary systems allow us to determine the internal structure constant (ISC), k2, which is a measure of the density variation within the star and is an important parameter of stellar evolution models. It is best studied in binary systems with eccentric orbits that show apsidal motion. The mean value of observed  is given by
is given by
where c21 and c22 are functions of the orbital eccentricity, fractional radii, masses of the components, and the ratio between rotational velocity of the stars and Keplerian velocity (Kopal 1978). The rotation of the stars was assumed to be synchronized with the maximum angular orbital velocity achieved at periastron. The astrophysical parameters of all systems are collected in Table 7.
The observed apsidal motion rate has two independent components: the Newtonian (classical) term, due to the non-spherical shape of both stars, and the relativistic term due to general relativity effects. Taking into account the value of the eccentricity and the masses of the components, a relativistic term,  , must first be subtracted. The original equation by Levi-Civita (1937) could be rewritten to be a more suitable function of known observable parameters, in degrees per cycle (Giménez 1985):
, must first be subtracted. The original equation by Levi-Civita (1937) could be rewritten to be a more suitable function of known observable parameters, in degrees per cycle (Giménez 1985):
where Mi denotes the individual masses of the components in solar units and P is the orbital period in days. The value of the classical contribution to the observed apsidal motion rate,  is then the following:
is then the following:
The values of  and the resulting mean internal structure constants
and the resulting mean internal structure constants  are given in Table 7. Their errors were determined using the relation derived in Wolf & Zejda (2005).
are given in Table 7. Their errors were determined using the relation derived in Wolf & Zejda (2005).
For PT Vel we used for comparison the theoretical values of the ISC, k2, theo from updated models according to the masses adopted and the chemical composition of Claret et al. (2021). These models assume convective core overshooting following the semi-empirical dependence on mass given by Claret & Torres (2018). For GM Nor and V397 Pup, we roughly estimated the theoretical value of k2, theo from the tables of Claret (2023, Tables 14–17) interpolating the given mass, expected age of the components (see Table 7 and conclusions below), and a mean chemical composition Z = 0.0134. The comparison of the theoretical and observed internal structure constant with previously studied binaries (Claret et al. 2021, their Table 3) is shown in Fig. 9.
 |
Fig. 9. Comparison of theoretical and observed internal structure constants of GM Nor, V397 Pup and PT Vel (red dots) with other systems collected in Claret et al. (2021, their Table 3). |
6. Conclusions
This study provides accurate information on the apsidal motion rates, absolute parameters, and observed ISC values for the three southern detached binary systems GM Nor, V397 Pup, and PT Vel. All derived or confirmed periods of apsidal motion are relatively short. The obtained values of the mean ISC  are compared to their theoretical values k2, theo according to the current theoretical models along the main sequence computed by Claret (2023). With the exception of PT Vel, the agreement is very good (see Fig. 9).
are compared to their theoretical values k2, theo according to the current theoretical models along the main sequence computed by Claret (2023). With the exception of PT Vel, the agreement is very good (see Fig. 9).
Our results for apsidal motion and light-curve analyses of GM Nor are similar to the previous parameters derived in Soderhjelm (1975). GM Nor also presents the shortest period of apsidal motion in our small sample (∼80 years). Most likely, the system consists of two similar stars of A3 ± 1 spectral type. It was also confirmed that V397 Pup is an EEB illustrated by a significant apsidal motion with a relatively short period of about 330 years. The precise masses of both components M1 = 3.08 M⊙ and M2 = 2.31 M⊙ were newly derived. For PT Vel, we found a slightly shorter apsidal motion period of U = 161 ± 13 years than that given in Bakış et al. (2008). Due to the limited coverage of the apsidal motion period in V397 Pup and PT Vel, additional observations over longer time periods are necessary to further constrain the results presented in this work. In this respect, our results should be considered as preliminary, since the characterization of these systems would still benefit from further photometric and spectroscopic observations.
The new and improved absolute dimensions of the components of V397 Pup and PT Vel are given in Table 7, with relative errors up to 3%. These values are sufficiently precise for comparison with current theoretical models. Their positions in the HR diagram that contains the evolutionary models for different masses according to Claret (2019) is plotted in Fig. 10. In the bottom part of this figure, the position of the components is compared with the set of isochrones calculated for the ages from 2 × 108 to 109 years, according to the CMD 3.7 web interface and the PARSEC 2.0 models (Bressan et al. 2012) available on the web pages of Osservatorio Astronomico di Padova16 Both systems, V397 Pup and PT Vel, are now part of an increasing group of eclipsing binaries with precise absolute dimensions that are suitable for subsequent tests. In these systems, no indications of the presence of a third component were observed. In the case of GM Nor, we do not yet know the precise absolute parameters. It would also be desirable to obtain new high-dispersion and high-S/N spectroscopic observations for GM Nor and to apply modern disentangling methods to obtain the radial velocity curve and derive accurate masses for this system.
 |
Fig. 10. HR diagram for components of studied binaries. Upper panel: models of stellar evolution according to Claret (2019) for masses of 1.8, 2.0, 2.5, and 3.0 M⊙ are plotted. Bottom panel: isochrones calculated for ages from 2 × 108 to 109 yr according to CMD 3.7 and PARSEC 2.0 models are given. |
Data availability
Tables A1–A5, and B1, and B2 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/A231
Motl, 2018, https://c-munipack.sourceforge.net/, ver. 2.1.24.
SImple LIght CUrve Processing System,
https://www.gxccd.com/cat?id = 187lang = 405
A Modern Mean Dwarf Stellar Color and Effective Temperature Sequence https://www.pas.rochester.edu/~emamajek/EEM_dwarf_UBVIJHK_colors_Teff.txt
Acknowledgments
Useful suggestions and recommendations from an anonymous referee helped improve the clarity of the article and are greatly appreciated. This investigation was supported by allocation of SAAO, MJUO and SPA observation time. Research of MW, PZ, JK and JM was partially supported by the project COOPERATIO – PHYSICS of the Charles University in Prague. This publication was produced within the framework of institutional support for the development of the research organization of Masaryk University. We wish to thank Alan C. Gilmore, Mt. John University Observatory, Dr. Alain Maury, SPACE Atacama Lodge, and the staff at SAAO for their warm hospitality and help with the equipment. The authors thank J. Juryšek and K. Hoňková, Variable Star and Exoplanet Section, for their important contribution to photometric observations with the FRAM telescope. This paper includes data collected by the TESS mission. The funding for the TESS mission is provided by the NASA Science Mission Directorate. Data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). We thank the Pierre Auger Collaboration for the use of its facilities. The operation of the FRAM robotic telescope was supported by the EU grant GLORIA (No. 283783 in FP7-Capacities program). This work is supported by MEYS (Czech Republic) under the projects MEYS LM2023032, CZ.02.1.01/0.0/0.0/16_013/0001402, CZ.02.1.01/0.0/0.0/18_046/0016010 and CZ.02.1.01/0.0/0.0/ 17_049/0008422 and CZ.02.01.01/00/22_008/0004632. This work is supported by grants GACR 24-13049S and CAS LQ100102401. This publication makes use of VOSA, developed under the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/ through the grant PID2020-112949GB-I00. VOSA has been partially updated using funding from the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement No. 776403 (EXOPLANETS-A). The following Internet-based resources were used in the research for this paper: the SIMBAD database operated at CDS, Strasbourg, France, the NASA’s Astrophysics Data System Bibliographic Services, the OMC Archive at LAEFF, preprocessed by ISDC. This investigation is part of an ongoing collaboration between professional astronomers and the Czech Astronomical Society, Variable Star and Exoplanet Section.
References
- Andersen, J. 1991, A&ARv, 3, 91 [Google Scholar]
- Avvakumova, E. A., Malkov, O. Y., & Kniazev, A. Y. 2013, Astron. Nachr., 334, 860 [Google Scholar]
- Bakış, V., Bakış, H., Demircan, O., & Eker, Z. 2008, MNRAS, 384, 1657 [Google Scholar]
- Baroch, D., Giménez, A., Ribas, I., et al. 2021, A&A, 649, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baroch, D., Giménez, A., Morales, J. C., et al. 2022, A&A, 665, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bulut, İ., & Demircan, O. 2007, MNRAS, 378, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2019, A&A, 628, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2023, A&A, 674, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Giménez, A. 2010, A&A, 519, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2018, ApJ, 859, 100 [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Claret, A., Giménez, A., Baroch, D., et al. 2021, A&A, 654, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruzalèbes, P., Petrov, R. G., Robbe-Dubois, S., et al. 2019, MNRAS, 490, 3158 [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [Google Scholar]
- Ebr, J., Janeček, P., Prouza, M., et al. 2014, Rev. Mex. Astron. Astrofis. Conf. Ser., 45, 114 [NASA ADS] [Google Scholar]
- Gaia Collaboration 2022, VizieR Online Data Catalog: I/355 [Google Scholar]
- Giménez, A. 1985, ApJ, 297, 405 [Google Scholar]
- Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [Google Scholar]
- Giménez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Harmanec, P., & Horn, J. 1998, J. Astron. Data, 4, 5 [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
- Kim, C. H., Kreiner, J. M., Zakrzewski, B., et al. 2018, ApJS, 235, 41 [Google Scholar]
- Kopal, Z. 1978, Dynamics of Close Binary Systems (Dordrecht: Reidel) [Google Scholar]
- Kruytbosch, W. E. 1932, Bull. Astron. Inst. Neth., 6, 233 [NASA ADS] [Google Scholar]
- Levi-Civita, T. 1937, Am. Jour. Math, 59, 225 [CrossRef] [Google Scholar]
- Malkov, O. Y., Oblak, E., Snegireva, E. A., & Torra, J. 2006, A&A, 446, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcussen, M. L., & Albrecht, S. H. 2022, ApJ, 933, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Mas-Hesse, J. M., Giménez, A., Domingo, A., et al. 2004, ESA Spec. Publ., 729 [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Menzies, J. W., Cousins, A. W. J., Banfield, R. M., & Laing, J. D. 1989, South African Astron. Obs. Circ., 13, 1 [Google Scholar]
- Otero, S. A. 2003, Inf. Bull. Variab. Stars, 5482, 1 [Google Scholar]
- Otero, S. A. 2005, Inf. Bull. Variab. Stars, 5631, 1 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Perryman, M. A. C., & ESA 1997, ESA Spec. Publ., 1200 [Google Scholar]
- Plaut, L. 1946, Bull. Astron. Inst. Neth., 10, 153 [NASA ADS] [Google Scholar]
- Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [Google Scholar]
- Prša, A. 2018, Modeling and Analysis of Eclipsing Binary Stars; The Theory and Design Principles of PHOEBE (Bristol: IOP Publishing) [Google Scholar]
- Prša, A., Kochoska, A., Conroy, K. E., et al. 2022, ApJS, 258, 16 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Savedoff, M. P. 1951, AJ, 56, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X.-D., Qian, S.-B., & Li, L.-J. 2022, ApJS, 259, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Soderhjelm, S. 1975, A&AS, 22, 263 [NASA ADS] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Strohmeier, W., Knigge, R., & Ott, H. 1964, Inf. Bull. Variab. Stars, 66, 1 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [Google Scholar]
- Wolf, M., & Zejda, M. 2005, A&A, 437, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, M., Zejda, M., & de Villiers, S. N. 2008, MNRAS, 388, 1836 [Google Scholar]
- Wolf, M., Zasche, P., Kučáková, H., et al. 2019, Acta Astron., 69, 63 [Google Scholar]
- Wolf, M., Zejda, M., Mašek, M., et al. 2022, New Astron., 92, 101708 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., Wolf, M., Vraštil, J., et al. 2014, A&A, 572, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
TESS visibility and sectors used for light curve analyses and for mid-eclipse time determination.
All Figures
 |
Fig. 1. Examples of our observations. Upper panel: observed differential V light curve of GM Nor obtained at SPA observatory (blue dots) in April 2010. Lower panel: observed VRI light curves of GM Nor obtained at Cape Town in 2020. The PHOEBE solutions are plotted as black curves. |
| In the text | |
 |
Fig. 2. Sample of 20 HARPS spectra of V397 Pup with prominent He4471 and Mg4481 absorption lines. |
| In the text | |
 |
Fig. 3. Historical O − C diagram of GM Nor together with our best-fit apsidal motion model. The blue solid curve and green circles correspond to the primary, the orange curve and yellow triangles to the secondary minima. Larger symbols denote the photoelectric or CCD measurements which were given higher weights in the calculations. The O − C2 residuals are plotted in the bottom panel. |
| In the text | |
 |
Fig. 4. O−C diagram for V397 Pup. See legend to Fig. 3. Although primary minima fit the curve well, the secondary have a larger scatter. Minima derived from TESS sectors are bulks of points close to epoch 3400, 3600 and 3800. |
| In the text | |
 |
Fig. 5. Current O − C diagram for PT Vel. See legend to Fig. 3. Numerous minima derived from TESS sectors are groups of points close to epoch 5700, 6100, and 6500. |
| In the text | |
 |
Fig. 6. TESS light curve of GM Nor obtained in Sector 12 (May/June 2019, orange circles) and its PHOEBE solution (black curve). The residuals from the solution are plotted in the bottom panel. |
| In the text | |
 |
Fig. 7. Solution of light and radial velocity curves for V397 Pup. Upper panel: TESS light curve (orange circles, binning 300) and its PHOEBE solution (black curve). Lower panel: radial velocity curve of V397 Pup and its PHOEBE solution (primary component in orange, secondary in blue). The residuals of the solution are plotted in the bottom panels. |
| In the text | |
 |
Fig. 8. Solution of light and radial velocity curves for PT Vel. Upper panel: TESS light curve (orange circles, binning 300) and its PHOEBE solution (black curve). Lower panel: Radial velocity curve of PT Vel obtained by Bakış et al. (2008) and new data, and its PHOEBE solution. Primary component in blue, secondary component in orange. The residuals of the solution are plotted in the bottom panels. |
| In the text | |
 |
Fig. 9. Comparison of theoretical and observed internal structure constants of GM Nor, V397 Pup and PT Vel (red dots) with other systems collected in Claret et al. (2021, their Table 3). |
| In the text | |
 |
Fig. 10. HR diagram for components of studied binaries. Upper panel: models of stellar evolution according to Claret (2019) for masses of 1.8, 2.0, 2.5, and 3.0 M⊙ are plotted. Bottom panel: isochrones calculated for ages from 2 × 108 to 109 yr according to CMD 3.7 and PARSEC 2.0 models are given. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.