© The Authors 2024

1. Introduction

The formation of supermassive black holes (SMBHs), especially those weighing ∼10⁹ M_⊙ at very high redshift, such as z ≳ 7 (e.g., recent observations by Bañados et al. 2018; Yang et al. 2020; Wang et al. 2021), has long been an intriguing astrophysical problem (e.g., recent reviews by Inayoshi et al. 2020; Volonteri et al. 2021). Observations have shown that these SMBHs grow from lighter “seed” BHs (Yu & Tremaine 2002). The seeds, typically in the mass range of intermediate-mass black holes (IMBHs; ∼100 − 10⁶ M_⊙), are proposed to form in multiple astrophysical scenarios, such as the direct collapse of pristine gas (e.g., Bromm & Loeb 2003; Latif et al. 2022), Population III star remnants (e.g., Madau & Rees 2001; Ryu et al. 2016), stellar-mass BHs that undergo hyper-Eddington accretion (e.g., Lupi et al. 2016, 2024; Pezzulli et al. 2016; Regan et al. 2019; Shi et al. 2023), and runaway stellar mergers in dense star clusters (e.g., Portegies Zwart et al. 2004; Kremer et al. 2020; Shi et al. 2021). If we use a reference radiative efficiency of 0.1, the e-folding timescale at the Eddington accretion rate is ∼45 Myr; on the other hand, due to the limited time allowed for SMBH formation (especially for z ≳ 7 quasars, which formed only ≲10⁹ yr after the Big Bang), a sustained phase of fast accretion is inevitable, possibly at super- or hyper-Eddington ($\gtrsim 500{\dot{M}}_{\mathrm{Edd}}$) accretion rates (Inayoshi et al. 2020)¹.

A number of theoretical works on small-scale BH accretion physics have shown that super-Eddington accretion is achievable and sustainable in principle within the BH accretion disk (Begelman 1979; Quataert & Gruzinov 2000; Blandford & Begelman 2004; Inayoshi et al. 2016). This is also supported by simulations with radiation hydrodynamics (RHD; Ohsuga et al. 2005), radiation megnetohydrodynamics (RMHD; Jiang et al. 2014, 2019), and general relativistic megnetohydrodynamics (GRMHD; Sądowski et al. 2015). However, these simulations typically embed the BH inside a gas reservoir with a sufficiently high mass-supply rate from large radii ($\gtrsim {10}^3{\dot{M}}_{\mathrm{Edd}}$). This level of gas feeding is not necessarily possible in more realistic star-forming astrophysical environments (which are much “larger-scale” compared to BH disks), because the gas medium may fragment due to self gravity and result in star formation, and feedback from newly formed stars – including radiative pressure, photoionization/heating, and winds – will develop turbulence or bulk motion in the medium (e.g., see star formation simulations Grudić et al. 2018, 2021a). Strong stellar feedback near an accreting BH may deplete the available fuel and challenge the feasibility of super-Eddington accretion (Dubois et al. 2015; Habouzit et al. 2017; Bower et al. 2017). Light seeds, like IMBHs or stellar-mass BHs, are especially prone to the accretion challenges inherent to these environments, because regimes influenced or even dominated by their gravity (i.e., the Bondi-Hoyle radius, Hoyle & Lyttleton 1939; Bondi 1952) are small compared with galactic scales.

To reconcile the problem, “larger-scale” (kpc or pc scale) simulations are not only required to model star formation and feedback in sufficient detail, but must also resolve the gas dynamics – below the gravitational capture scale (Bondi-Hoyle radius) – of at least some rapid-accreting BHs. In Shi et al. (2023, Paper I hereafter), we made some first steps toward addressing this problem using simulations of star formation and feedback in giant molecular clouds (GMCs) similar to that in Grudić et al. (2018), and studying BH seed growth in the absence of BH feedback. Although the stellar feedback makes the GMC uneven and turbulent, it also generates dense clumps and shocks (Klessen 2000), which may have low internal velocity dispersion (Mac Low & Klessen 2004; McKee & Ostriker 2007); these factors mean that the simulation is able to resolve the gravitational capture of gas for some “lucky” BHs encountering dense gas clumps with small relative velocity, because the Bondi-Hoyle radii are large under these circumstances. Similar to the star formation efficiency explored in the literature (Grudić et al. 2018, 2021a; Kim et al. 2018; He et al. 2019; Fukushima et al. 2020; Kim et al. 2021; Chevance et al. 2023), BH accretion is also regulated by the surface density (Σ₀ ≡ M_cl/πR_cl²) of the cloud: higher Σ₀ means higher self-gravity (∼GM_cl/R_cl² ∼ πGΣ₀), which keeps the cloud bound rather than disrupted by stellar feedback. Paper I found that for clouds with high surface density (Σ₀ ≈ 10⁴ M_⊙ pc⁻²), the gas supply reaching the accretion disk of the BH could be sufficient to support hyper-Eddington accretion with $f_{\mathrm{Edd}}\equiv {\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}\sim 1000$ for at least a small but non-negligible number of seeds.

More realistically, BH feedback mechanisms, such as electromagnetic radiation (Fabian 2012; Hopkins et al. 2016), winds and jets (Silk & Rees 1998; Murray et al. 2005; Di Matteo et al. 2005; Ostriker et al. 2010; Sądowski et al. 2016; Torrey et al. 2020; Hu et al. 2022; Massonneau et al. 2023), and cosmic rays (CRs; Sijacki et al. 2008; Guo & Mathews 2012; Zweibel 2017; Su et al. 2021; Ishibashi & Fabian 2023) will deposit energy and mechanical momentum back to the gas reservoir. The energy and momentum heat and deplete the gas fuel, or even prevent its infall to the BH (Dubois et al. 2013), potentially challenging the hyper-Eddington accretion scenario. Still, close to the BH (≲1000 r_Sch), at sufficiently high accretion rates and opacities, photons are effectively trapped with the inflow, which means the radiated energy (Watarai et al. 2000; Madau et al. 2014, and other references above) will only grow sublinearly with the accretion rate (measured as ${\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}$). This is also true for the mass outflow powered by radiation (Hu et al. 2022). As a result, the feedback strength at high accretion rates is suppressed and hyper-Eddington accretion could remain possible.

Though BH feedback is not included in the simulations of Paper I, an estimate was made in terms of radiative feedback based on the density criteria for hyper-Eddington accretion predicted by Inayoshi et al. (2016): n_∞ ≳ 10⁵(M_BH/10⁴ M_⊙)⁻¹(T_∞/10⁴ K)^3/2 cm⁻³, where n_∞ and T_∞ are the density and temperature of gas “near” the BH (at sub-pc scales). For BHs in simulations that grow rapidly, especially those inside GMCs with Σ₀ ≈ 10⁴ M_⊙ pc⁻², the ambient gas density is above this critical value, which suggests hyper-Eddington accretion may be achievable even if there is radiative feedback. Still, there is a necessity to include BH radiative feedback in simulations like that of Paper I for completeness, because BH feedback may still affect GMC behaviors at larger scales. The influence of other forms of BH feedback, such as mechanical feedback and cosmic rays, on accretion is also to be determined.

In this article, we extend the discussion of Paper I and explore the impact of multiple BH feedback mechanisms, including radiation, mechanical outflow, and CRs. In particular, we are interested in how the BH feedback mechanisms determine the maximum mass a BH can reach from accretion, and how they scale in different GMCs. To reach this goal, we ran a suite of numerical simulations by adopting the basic setups and physics involved in Paper I where the authors showed hyper-Eddington accretion was possible without BH feedback, but with a new subgrid BH accretion and feedback model, as well as related physics.

The article is organized as follows. In Sect. 2, we introduce the background and implementations of BH accretion and feedback, as well as the simulation initial conditions. In Sect. 3, we present our fiducial feedback model results and explore the effects of different accretion and feedback physics. In Sect. 4, we discuss the results and important caveats of our simulations. Finally, we conclude in Sect. 5.

2. Background and method

This study follows the basic framework of Paper I: each simulation is initialized with a number of seed BHs inside a precollapse pre-star-formation parsec-scale GMC, and then evolves self-consistently with MHD+gravity and additional physics, including star formation and its feedback, BH accretion and its feedback, and so on.

2.1. Overview

Our simulation follows the same numerical framework for star formation and feedback as that in previous star-formation simulations (Grudić et al. 2018, 2021b) and the previous study of this series (Paper I). As a short summary, we use the meshless, Lagrangian, Godunov MHD code GIZMO (Hopkins 2015, 2016; Hopkins & Raives 2016) in its Meshless Finite Mass (MFM) mode, including the physics of self-gravity, radiative cooling, star formation, and feedback. In particular, star formation and feedback are based on the FIRE-3 implementation of the Feedback In Realistic Environments² (FIRE) framework (Hopkins et al. 2018a, 2023). Each “star” particle in the simulation represents an IMF-averaged ensemble of stars, which evolves and deposits mass outflow, metals, and radiation back to the ISM as its feedback (Hopkins et al. 2018b). This treatment has been shown to reasonably reproduce many of the properties of star formation in GMCs, such as the star formation efficiency, star cluster dynamics, and cluster mass distribution (Grudić et al. 2018, 2021b).

The simulation also follows the same scheme for BH accretion from gravitational capture as that in Paper I, which is based on that stated in Grudić et al. (2021a): gas cells are captured by a BH if (i) they are within a preset “sink radius” near the BH, (ii) they are gravitationally bound to the BH, and (iii) their individual Keplerian orbit is within the sink radius (Bate et al. 1995). Moreover, we choose the softening radius of BHs to be the same as their sink radius and set the value to make sure that the Bondi-Hoyle accretion radius is resolved (i.e., greater than the sink radius) for fast-accreting BHs, which is extensively discussed in Paper I.

For this study, we extend the BH accretion scheme with a sub-grid model of BH accretion to account for BH feedback. To help explain this, we present a schematic view of the simulation in Fig. 1. Accretion onto a BH can be decomposed into two successive phases: (i) the gravitational capture of gas from the surrounding ISM (as a reservoir), or from approximately parsec to subparsec scales, as studied in Paper I and resolved in our simulations here; (ii) the mass transfer from the BH accretion disk (as a secondary reservoir) to the event horizon, or from subparsec to approximately km (or r_Sch) scales, which we do not resolve in our simulations. Along with the accretion, gravitational energy is transformed into other forms of energy, like radiation, winds/jets, and cosmic rays.

At the second phase (smaller scales), not all of the mass and energy flows reach the BH: (i) some fraction of the accretion flow will be powered by kinetic and/or radiative pressure and form jets and/or winds; (ii) some fraction of the energy “leaks” from the disk and is deposited into the GMC in the form of radiation and CRs. As a result, intuitively BH feedback mechanisms typically serve as negative factors that suppress the BH accretion in two ways: (i) reducing the final mass transfer rate onto the BH due to energy and mass loss; and (ii) preventing additional gas in GMC from accreting.

Moreover, there is thus a huge mismatch among the scales and physics involved, and the second process is beyond the resolution limit (∼0.1 pc) of our MHD simulation. We therefore treat this with a subgrid model: the BH sink particle accretes gas from the parent simulation on resolved scales, stores the mass inside a gas reservoir (or disk), and then transfers the mass to the BH at a rate ${\dot{M}}_{\mathrm{dep}}$, which is also used to calculate mass and energy flow rates for different feedback mechanisms.

Details of the subgrid model are expanded below, following the schematic “order” of mass flow from the disk to the BH shown in Fig. 1. However, we note that the “order” is only for defining quantities like the mass loading factor and energy efficiency, not in the chronological sense. 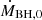Moreover, as the feedback energy efficiency (defined as the ratio between the outflow energy and ${\dot{M}}_{\mathrm{BH}}{c}^2$) is typically very small (at most 0.1) in the simulation, we treat ${\dot{M}}_{\mathrm{BH},0}$ and Ṁ_BH interchangeably in the simulation and this article, without impacting our results, at least in the order-of-magnitude sense. For example, although the radiation power is defined as L_bol ≡ ϵ_rM_BH, 0c² in Fig. 1, the relation L_bol ≐ ϵ_rM_BHc² still holds as a very good approximation.

Fig. 1. Mass and energy flow of BH accretion and feedback. This study extends the framework of star formation in Grudić et al. (2018) and BH accretion without feedback in Paper I. To implement BH feedback, we use a model of mass transfer from the disk to the BH. With only a fraction of the accretion flow going to the BH, other portions are deposited back to the GMC in the form of radiation, jets and winds, and cosmic rays. We note that since the feedback energy efficiencies are typically small (≲0.1), ${\dot{M}}_{\mathrm{BH}}\doteq {\dot{M}}_{\mathrm{BH},0}$.

2.2. Subgrid models for BH accretion and feedback

2.2.1. Disk-mass depletion

As shown in the flowchart of Fig. 1, gas is captured by sink particles via resolved gravitational accretion. It is then added to a “reservoir” of mass M_d – which we refer to as the disk – surrounding the BH of mass M_BH. We require a subgrid model for the accretion rate ${\dot{M}}_{\mathrm{d}}$ from the disk to the BH, because this determines the feedback properties, and so we define ${\dot{M}}_{\mathrm{d}}=M_{\mathrm{d}}/t_{\mathrm{dep}}$ in terms of the depletion time t_dep.

The classical way to describe the BH accretion disk is with the thin-disk model (Shakura & Sunyaev 1973), where the accretion rate follows

$$\begin{array}{c}\hfill \dot{M}\sim 2\pi \alpha {\mathrm{\Sigma }}_{\mathrm{d}}{c}_{\mathrm{s}}^2/{\mathrm{\Omega }}_{\mathrm{K}}.\end{array}$$(1)

Here, Σ_d, c_s, and Ω_K are respectively the surface density, sound speed, and Keplerian frequency at a certain radius of the disk; α is a dimensionless constant that characterizes the effective viscosity. Motivated heuristically by Eq. (1), we set

$$\begin{array}{c}\hfill t_{\mathrm{dep}}=t_{\mathrm{dyn},\mathrm{sink}}/(2\pi \alpha ).\end{array}$$(2)

We note that we redefined α by absorbing the factor of (Ω_Kr_sink/c_s)² and other constants. Here t_dyn, sink ≡ [r_sink³/G(M_BH + M_d)]^1/2 is the dynamical timescale of a test particle at the sink radius, which is the fastest possible mass-depletion time. By varying α, we may bracket different conditions, including slow and fast mass-depletion rates.

We caution that for realistic BH accretion, the mass-inflow rate can be dependent on the radius, because there is mass outflow in the form of winds (Blandford & Begelman 1999; Hu et al. 2022). Although in Eq. (1) we assume a scale-independent mass-inflow rate, the effect of BH wind feedback is indeed considered (see following subsection), where we assume only a fraction of the mass can reach the BH, while the remaining mass is deposited back to the GMC in the form of wind and jet.

In the simulation, we also add two constraints to the BH mass transfer. We first set a maximum mass of the accretion disk to represent effects such as fragmentation, which limits accretion if mass “stalls” in the disk; this mass is quantified by the upper limit of M_d/M_BH. Once M_d reaches this limit, no gas cells will be absorbed by the BH in the next time step. Secondly, there is also an upper limit on the Eddington ratio, which is defined as $f_{\mathrm{Edd}}\equiv {\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}$. We vary the upper limit M_d/M_BH. Due to our particular interest in hyper-Eddington accretion, which is predicted to be extreme (Inayoshi et al. 2020), we fix the upper limit of f_Edd to 1000, but obtain qualitatively similar results so long as this limit is ≫1, as we discuss below.

2.2.2. Mechanical feedback

In this simulation, we treat the mass and energy flow as shown in Fig. 1. For a given ${\dot{M}}_{\mathrm{dep}}$, we assume some fraction of this will be ejected in the form of winds, outflows, and/or jets, which we combine here as “mechanical” outflow and simply refer to as “winds” throughout. We define the jet mass loading factor as ${\eta }_{\mathrm{w}}\equiv {\dot{M}}_{\mathrm{w}}/{\dot{M}}_{\mathrm{BH},0}$, where ${\dot{M}}_{\mathrm{w}}$ is the jet-mass-outflow rate, and so ${\dot{M}}_{\mathrm{w}}={\dot{M}}_{\mathrm{dep}}·{\eta }_{\mathrm{w}}/(1+{\eta }_{\mathrm{w}})$. The kinetic luminosity of the winds can be parameterized with a coefficient ϵ_w, such that $L_{\mathrm{w}}={ϵ}_{\mathrm{w}}{\dot{M}}_{\mathrm{BH},0}{c}^2$, or with effective outflow velocity v_w, where L_w = M_wv_w²/2.

For fiducial simulations, we set η_w = 1 and a characteristic ϵ_w such that the mechanical feedback energy is capable of disrupting the whole cloud, that is, the accumulated jet energy fills the potential well of the GMC: ${\displaystyle \int {ϵ}_{\mathrm{w}}{\dot{M}}_{\mathrm{BH},0}}{c}^2\mathrm{d}t\sim G{M}_{\mathrm{cl}}^2/R_{\mathrm{cl}}$. Treating ϵ_w as a constant, we integrate over the BH accretion history and find the LHS turns into ϵ_wΔM_BH, 0c², where ΔM_BH, 0 is the total mass of gas reaching the inner disk near the event horizon. We choose a characteristic value of ΔM_BH, c = 10⁴ M_⊙. The characteristic ϵ_w is then ϵ_w, c = M_cl/ΔM_BH, c(v_cl/c)². Here, v_cl² = GM_cl/R_cl is the characteristic circular velocity of the cloud. Following the energy argument we assume above, if ϵ_w ≪ ϵ_w, c then the mechanical feedback is insignificant; while if ϵ_w ≫ ϵ_w, c, the strong mass outflow may disrupt the GMC quickly. This also implies a critical jet velocity at the critical jet luminosity of $v_{\mathrm{w},\mathrm{c}}=v_{\mathrm{cl}}\sqrt{M_{\mathrm{cl}}/\mathrm{\Delta }{M}_{\mathrm{BH},\mathrm{c}}}$.

Motivated by simulations of hyper-Eddington accretion (Sądowski et al. 2016), we assume fiducial η_w = 1 but vary v_w widely. Moreover, some small-scale simulations fit subgrid models, which vary η_w as a function of the accretion rate. In this work, we implemented a version presented in Hu et al. (2022), which roughly sets η_w = f_Edd − 1 (where $f_{\mathrm{Edd}}\equiv {\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}$) while keeping a nearly constant kinetic energy output of $E_{\mathrm{kin}}\approx 4\times {10}^{-4}{\dot{M}}_{\mathrm{Edd}}{c}^2$ at the super-Eddington regime of f_Edd ≳ 3.

Numerically, the winds and jets in the simulation are implemented as high-resolution gas cells that are ejected in a bipolar fashion from the BH (Torrey et al. 2020). In the rest frame of the BH, these gas cells are ejected along the spin of the BH, which is further determined by the accumulated angular momentum of the gas. A similar implementation was also used and described in Su et al. (2021) and Grudić et al. (2021a).

2.2.3. Radiative feedback

Given some remaining accretion rate ${\dot{M}}_{\mathrm{BH},0}$ (after the loss of winds from ${\dot{M}}_{\mathrm{dep}}$), we can calculate the bolometric accretion disk luminosity L_bol in terms of some radiative efficiency: $L_{\mathrm{bol}}={ϵ}_{\mathrm{r}}{\dot{M}}_{\mathrm{Edd}}{c}^2$. Given L_bol, we explicitly model the outgoing BH spectrum – based on the template in Shen et al. (2020) – and its effects in our multiband (X-ray, extreme-ultraviolet, far-ultraviolet, near-ultraviolet, optical-infrared, and far-infrared) radiation treatment (similar to that used in Hopkins et al. 2020), including its effects on photo-ionization and photo-heating, Compton heating, and radiation pressure on gas and dust, as described in Hopkins et al. (2023).

Analytical studies and numerical simulations have shown that due to the photon-trapping effect on small scales near BHs, the bolometric luminosity grows slowly with increasing accretion rate (rescaled to $f_{\mathrm{Edd}}\equiv {\dot{M}}_{\mathrm{BH},0}/{\dot{M}}_{\mathrm{Edd}}$), typically in logarithmic form. For this reason, super-Eddington accretion is not limited by the radiative energy loss (Madau et al. 2014).

In our simulation, we therefore compare various constant-ϵ_r choices with two models for variable ϵ_r (as shown in Fig. 2). The first one by Watarai et al. (2000) is analytically derived from the thin disk model, which features a linear form at low accretion rate (with contact ϵ_r = 0.1) and a logarithm form at high accretion rate. Another form is fitted by Madau et al. (2014) from original simulations of relativistic slim disks in Sądowski (2009); this form features dependence on the BH spin parameter a. We set a = 0 for this form in our simulation because Madau et al. (2014) found that the super-Eddington accretion e-folding time is nearly independent of a.

Fig. 2. Subgrid models for radiative feedback (top panel) and mechanical feedback (bottom two panels). Top: Energy- and momentum-ejection rates as a function of accretion rates, including “log-form” models inferred from the slim disk (solid), and simple ones with constant ${ϵ}_{\mathrm{r}}\equiv L/({\dot{M}}_{\mathrm{BH}}{c}^2)$ (dashed). Bottom: Momentum-ejection rates for mechanical feedback with constant ${ϵ}_{\mathrm{w}}\equiv {\dot{E}}_{\mathrm{kin}}/({\dot{M}}_{\mathrm{BH}}{c}^2)$ (dashed), and the model in Hu et al. (2022) – though the released kinetic energy is almost constant ($E_{\mathrm{kin}}\approx 4\times {10}^{-4}{\dot{M}}_{\mathrm{Edd}}{c}^2$), the momentum-injection rate grows linearly ($\dot{p}\approx 0.03f_{\mathrm{Edd}}{\dot{M}}_{\mathrm{Edd}}c$) because of the variable mass-loading factor.

2.2.4. Cosmic rays

Previous simulations have highlighted the possible importance of CRs (ultrarelativistic particles) accelerated around BHs or jets (Sijacki et al. 2008; Guo & Mathews 2012; Su et al. 2021). In addition, CRs also lose energy due to Coulomb interactions, ionization, and catastrophic losses, which also heat the ambient gas (e.g., Guo & Oh 2008).

In this study, we simulate CRs based on implementations described in Hopkins et al. (2022) – representing them as a “single bin” (relativistic ∼1 − 10 GeV protons) –, which obey a two-moment streaming+diffusion+acceleration equation, with Alfvenic streaming and a fiducial scattering rate set to ν ∼ 10⁹ s⁻¹ calibrated to Solar System and Milky Way CR observations (from Voyager, Fermi, and AMS-02; see, Hopkins et al. 2022). All relevant cosmic-ray loss or cooling, and gas coupling, scattering, ionization, and heating details are included as described in this latter publication.

In our simulations, the CR feedback from BHs is coupled with the mechanical feedback (i.e., the CR energy is deposited to the newly spawned jet cells). We vary the strength of the BH CR feedback through its energy-loading coefficient ϵ_CR, which is defined by the injection rate $L_{\mathrm{CR}}={ϵ}_{\mathrm{CR}}{\dot{M}}_{\mathrm{BH},0}{c}^2$. Additionally, for each simulation with the BH CR feedback, we set a constant CR energy-ejection rate of 10% for SNe in order to account for the CR feedback from stars. This particular effect is not considered in other sets of simulations without CRs.

2.3. Initial simulation conditions

We use the same initial conditions (ICs) for GMCs as in Paper I, but only choose GMCs with the highest initial surface density (Σ₀ = 13 000 M_⊙/pc²), with different radii (5 or 50 pc) and therefore different masses (10⁶ or 10⁸ M_⊙). These are chosen as the clouds in Paper I, where BHs accrete significantly without BH feedback, while other cases would be unlikely to see significant mass growth with the feedback physics. The clouds are initially of solar metallicity (Z_⊙) in the fiducial case. The ICs are listed in Table 1. The time limit for each simulation is 2.5 t_ff, where t_ff = [R_cl³/(8GM_cl)]^1/2 is the initial free-fall time of the cloud. For each mass group, there are low (initially with 64³ equal-mass gas cells) and high (128³) resolution runs. Force softening is set as described in Paper I.

Each simulation is initialized with a number of BH seeds with random mass, position, and velocity, which are sampled following the same method as in Paper I: BHs are randomly distributed following a uniform spatial distribution within the volume; the initial velocity magnitude is confined to be below the local circular velocity (for discussions on these choices, see, Shi et al. 2023). In particular, the BH mass follows a log-uniform distribution within 10 (100)–1000 M_⊙ (10⁴ M_⊙) for the 10⁶ M_⊙ (10⁸ M_⊙) cloud, which covers the range of stellar-mass BHs and IMBHs.

The independent parameters we vary to quantify the impact of BH feedback are listed in Table 2. For each parameter, we set a fiducial value as the “baseline” and vary each parameter in turn.

3. Results

3.1. Fiducial results: Radiative-inefficient models

Compared with Paper I, we include a “log-form” radiative-inefficient model (Madau et al. 2014) to account for the radiative feedback from slim disks and a constant wind energy efficiency. This naturally causes a suppression in the mass-accretion rate of seed BHs (as described in Sect. 3.2). Here we focus on the two simulations of 10⁶ M_⊙ and 10⁸ M_⊙ cloud complexes with “high resolution” (initially with 128³ gas cells; see Table 1).

As a first impression, Fig. 3 compares the gas morphology of simulations with and without BH feedback at different scales. From left to right, we zoom onto a selected BH experiencing significant mass accretion. The particular BH that accreted the most mass throughout the simulation time range, and the snapshot shown, are also chosen when that BH is in its fastest-accreting phase. Each panel shows the line-of-sight averaged density, which is defined as ∫ρ(s)ds/∫ds. At the smallest scales (panels in the right column), we evaluate v_gas − v_BH and show the velocity field within a thin layer of one-eighth of the field of view (centered at the BH) on top of the density field.

Fig. 3. Visualization of simulations with and without BH feedback physics, each from a snapshot when a BH is undergoing rapid growth. Left two zoom-in plots: Gas morphology for the 106 M⊙ GMCs without (top) or with (bottom) BH feedback. From left to right, we zoom into a BH undergoing hyper-Eddington accretion. As the smallest scale, each panel shows the velocity field near the BH, with the circular velocity ($\sqrt{G{M}_{\mathrm{cl}}/R_{\mathrm{cl}}}$) presented as a gauge. Right two zoom-in plots: Same as the left plots, but for the 108 M⊙ GMC.

As also suggested in Paper I, the fast-growing BH seed is often near a dense gas clump (ρ ≳ 10⁵ M_⊙/pc³, typically more than 100 times denser than the mean density), and has a small relative velocity of |v_gas − v_BH|< |v_BH|, which ensures efficient gravitational capture of gas. Despite feedback from BHs, these features are also observed in corresponding simulations of both 10⁶ M_⊙ and 10⁸ M_⊙ complexes, which also fit the expectations of the Bondi-Hoyle accretion.

In the absence of BH feedback, the gas in the simulations is relatively dense. Additionally, near the accreting BH without feedback (see the first and third rows of Fig. 3), there are features like disks and spiral arms at approximately parsec scales at late times, which means that there is coherent gas inflow due to the potential well of the GMC. At this time, there is also star formation in the 10⁶ M_⊙ GMC near the BH, creating a cavity in the gas distribution (see the first row of Fig. 3), though not observed in the 10⁸ M_⊙ GMC through the simulation time. In contrast, when BH feedback is turned on, additional bubbles, outflows, sheets, and clumps appear and the inflow is relatively incoherent.

Figure 4 shows the BH mass-growth history in both fiducial simulations, by selecting five seed BHs with the highest final-to-initial mass ratios. For each BH, both the BH-only mass and the sink-particle (BH+disk) mass are shown. As in Paper I, single BHs grow rapidly when they encounter dense clumps, while the accretion rate is low most of the time.

Fig. 4. Mass evolution and accretion rate for BH particles in different GMCs. In the first and third panels (from top to bottom), we select five BHs with significant mass growth from high-resolution simulations of the two complexes and plot the evolution of the mass bound to the BH (BH+disk, solid) and the BH-only mass (dashed). In the second and fourth panels, we show the accretion rate for the same BHs, each rescaled to its Eddington accretion rate ($f_{\mathrm{Edd}}={\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}$).

We see little difference in BH-only mass and sink-particle mass at the early stage of the evolution when the BH accretion rate is low. If the BH feedback is significantly strong, the overall mass accretion is suppressed, and the BH accretion is determined by the material that is already bound to its gravity. Due to the timescale for mass transfer from the disk to the BH, there is a “phase lag” between M_BH and M_sink, but the effect is not significant in our fiducial model.

For single BHs, the BH mass-accretion rates Ṁ_BH (the actual accretion rate arriving at the BH) are also shown in Fig. 4. We scale the rate in units of the Eddington rate for each BH. Here we show the same five BHs as those selected in Fig. 4. These samples typically reach hyper-Eddington accretion abruptly at some time in their evolution and maintain the status for a short period of time (∼0.1 t_ff), during which time Ṁ_BH is capped by the upper limit set in the code. Once the fast-accretion phase is terminated, the mass transfer from the disk to the BH declines with the characteristic scale of t_dep as defined in Sect. 2.

Thus, from Fig. 4, there is evidence that hyper-Eddington accretion is achievable for BHs in the dense complexes we simulated, even with BH feedback. However, the BH feedback can have a negative impact on accretion, which we quantify in Sect. 3.2.

Fig. 5. Cumulative distribution function of the accreted mass, Eddington ratio, and bolometric luminosity for BH populations in simulations with the fiducial BH feedback setups. In the right two panels, we show the distribution of the “peak” value throughout the evolution. Both the high- (solid) and low-resolution (dashed) simulations are displayed and show qualitatively similar trends. The artificial flat “plateau” at the left of some lines reflects the mass-resolution limit of that simulation.

Fig. 6. Dependence of BH accretion on initial conditions of BHs. From our high-resolution fiducial simulations, we mark BHs with resolved accretion in a phase space of the accreted mass (ΔMBH) versus the initial mass ($M_{\mathrm{BH}}^{\mathrm{ini}}$), distance to the cloud’s center ($r_{\mathrm{BH}}^{\mathrm{ini}}$), velocity ($v_{\mathrm{BH}}^{\mathrm{ini}}$), and specific angular momentum ($j_{\mathrm{BH}}^{\mathrm{ini}}$). We find only a weak dependence on these initial conditions. We may also clearly see the mass-resolution limit from the lower “cutoff” in ΔMBH for the 108 M⊙ complex.

Figure 5 shows the cumulative distribution function (CDF) of ΔM_BH (relative mass growth at the end of the simulation of each BH) measured from simulations. As expected in Paper I, only a modest fraction (≲10%) of BH seeds have appreciable mass accretion at the resolution used here. Comparing the two GMCs, we find that BHs in the 10⁸ M_⊙ GMC have much more significant mass growth, which is again expected from Paper I. Moreover, we compared the low- and high-resolution simulations with the same BH feedback recipes in the same figure, and find a qualitatively similar distribution.

Throughout the simulation, we find these BHs with resolved accretion activity typically reach super-Eddington accretion at some stage of the evolution, and a small fraction (∼1%) of the total number of BHs can even reach the preset cap (f_Edd ≥ 1000). We also check the bolometric luminosity, defined as $L_{\mathrm{bol}}={ϵ}_{\mathrm{r}}(f_{\mathrm{Edd}}){\dot{M}}_{\mathrm{BH}}{c}^2$. For the 10⁶ M_⊙ complex, BHs can emit radiation at ∼10⁴² erg/s at some stage of their evolution, while the value can be ∼10⁴² − 10⁴³ erg/s for BHs in the 10⁸ M_⊙ complex.

For BHs in these two complexes, the CDFs of ΔM_BH and L_bol are very similar despite different mass resolutions and number of sampling points (i.e., the number of seed BHs in each simulation). We find that the distribution function of ΔM_BH can be well fitted with a log-normal distribution: f(ΔM_BH)∝exp[−log(ΔM_BH/μ)²/(2s²)]. For both fiducial runs of the 10⁶ M_⊙ and 10⁸ M_⊙ complexes, the best-fit parameters are approximately μ = 10^−2.5 M_⊙, s = 2.25. Explicitly, the CDF of ΔM_BH [M_⊙] is

$$\begin{array}{c}\hfill P(\mathrm{\Delta }{M}_{\mathrm{BH}}>x)=\frac{1}{2}[1-\mathrm{erf}\left(\frac{logx+2.5}{2.25\sqrt{2}}\right)]·\end{array}$$(3)

In Paper I, we demonstrate that there is a weak dependence of the results on the initial properties of BH seeds, such as their initial mass, position, and velocity magnitude, as long as they are gravitationally bound to the cloud. Similarly, we explore this same dependence for our new simulations by checking ΔM_BH for each BH at the end of the simulation. In each panel of Fig. 6, we list the initial mass, distance to the GMC center, velocity magnitude, and specific angular momentum of the BH. Again, for both the 10⁶ M_⊙ and 10⁸ M_⊙ cloud, there is no (or little) correlation with ΔM_sink. The result means that BH accretion in a turbulent environment is stochastic and much information from the initial condition is smeared in the process. This is why we simulated N_BH ≫ 1 seeds in each cloud – there is only a ∼1 − 10% probability of a seed being “lucky” and encountering a dense clump for accretion.

From the same figure, we see that BH accretion has no strong dependence on the initial position or velocity. However, the last panel shows stronger evidence that BHs with significant mass growth tend to have low initial specific angular momentum ($\lesssim 0.2\sqrt{G{M}_{\mathrm{cl}}{R}_{\mathrm{cl}}}$). This is expected from the evolution of the cloud, because the gravitational collapse brings dense gas inward, and only BH seeds with low specific angular momentum can reach the inner part of the complex.

3.2. Parameter survey: Effects of different physics

To check the effects of different physics, we performed a parameter survey, varying parameters in our subgrid model as listed in Table 2. Taking into consideration the computational cost, we performed these simulations at low resolution (see Table 1).

Fig. 7. Parameter survey of the accretion model, using an effective α-parameter to quantify the accretion rate. Here we vary α and the upper limit on disk mass. In the fiducial case (dashed), α = 0.1 and Md/MBH ≤ 10.

Fig. 8. Parameter survey of the energy efficiency in different feedback mechanisms based on experiments with the 106 M⊙ complex. From left to right, the three columns show the CDF of accreted mass by BHs, as well as the highest possible fEdd and Lbol throughout the evolution. Each row represents a set of simulations with varying models of a specific feedback mechanism (labeled in each left panel), with the fiducial model marked in black dashed lines.

3.2.1. Subgrid accretion model

In Fig. 7 we show the effect of free parameters on the disk-mass depletion: the upper limit of M_d/M_BH and the effective α parameter for viscosity. In this plot, we show the CDF of the change in BH+disk and the BH-only mass, as well as the CDF of the Eddington ratio for BHs throughout their evolution. Comparing the fiducial case, enforcing a smaller upper limit of M_d/M_BH ≤ 1 leads to a lower amount of accreted mass by a factor of ∼10, and fewer BHs can reach hyper-Eddington accretion. This is a natural consequence of the smaller disk mass, which means that less mass can reach the BH+disk system. Because the mass comes in rapidly, it must either be able to accrete extremely rapidly through the disk (α > 1) or be able to avoid fragmentation and star formation (M_d/M_BH > 1) in order to reach the “full” potential growth. However, we stress that we still clearly see hyper-Eddington accretion for M_d/M_BH ≤ 1.

We then tested higher (1) or lower (0.01) values of the α parameter, in contrast with the fiducial one (0.1). As shown in Eq. (1), smaller α means slower mass transfer from the disk to the BH, and this is true in our tests: by fixing M_d/M_BH ≤ 10, there is a larger deviation between the BH+disk curve and the BH-only curve in the mass CDF once α is smaller, and the Eddington ratio is typically lower for smaller α. The trend is also true for tests with fixed M_d/M_BH ≤ 1.

The parameter α also affects the mass accretion onto the BH+disk system in the simulation. If α is low, the feedback is also weaker due to less mass reaching the BH; if α is high, mass depletion from the disk is efficient and the disk mass can be supplemented quickly in a very gas-rich environment. Both effects are positive factors for accumulating more mass in the BH+disk system. This argument is also reflected in Fig. 7 when comparing tests with different α, where α = 1 and α = 0.01 tests sometimes have more mass accretion than the fiducial α = 0.1 case. Still, we show below that none of these effects in the subgrid accretion model are as dominate as the largest variations in the strength of feedback.

Fig. 9. Parameter survey of the energy efficiency in different feedback mechanisms based on experiments with the 108 M⊙ cloud complex. Conventions are the same as those in Fig. 8.

3.2.2. Radiative feedback and metallicity

We study the effect of radiative feedback by varying its energy efficiency ϵ_r, including two “log-form” accretion-rate-dependent models from Watarai et al. (2000) and Madau et al. (2014), as well as fixed ϵ_r at 10⁻⁹ − 0.1. Similar to the layout of Fig. 5, the top panels of Figs. 8 and 9 show the CDF of accreted mass, the Eddington ratio, and the bolometric luminosity of the BH population.

Comparing fixed-value energy efficiencies, there is a clear trend in that, once ϵ_r ≳ 10⁻³ (10⁻¹) for the 10⁶ M_⊙ (10⁸ M_⊙) GMC, the accretion onto BHs is suppressed. The same behavior appears in the Eddington ratio. Despite relatively strong feedback, 1% of BHs reach the preset cap in the Eddington ratio in many simulations, while the fraction of these BHs drops when the feedback is strong. Finally, the luminosity of BHs typically increases with radiative efficiency, as expected.

As also shown in Fig. 2, the radiative efficiency at high accretion rates (f_Edd = 1000) can be as low as 3 × 10⁻² for Madau et al. (2014) and 10⁻² for Watarai et al. (2000). Comparing simulations with fixed-value efficiencies, we find that these radiatively inefficient models behave very similarly to those with fixed ϵ_r = 10⁻³ and ϵ_r = 10⁻². The feedback strength is thus mainly dominated by the hyper-Eddington regime for these models. As a result, the Madau et al. (2014) model is less feedback-dominated.

We further studied the impact of the GMC’s initial metallicity. In the no-BH-feedback case studied in Paper I, experiments with different initial metallicity found no (or little) correlation between BH accretion and initial metallicity. However, higher metallicity means tighter coupling between the radiation and wind because of more dust grains in the ISM, which may imply stronger radiative pressure (e.g., Larson & Starrfield 1971); this is one of the radiative feedback mechanisms (alongside heating and photoionization) implemented in the simulation. In this study, we vary the initial metallicity for two kinds of radiative models: the fiducial Madau et al. (2014) model and the fixed-value ϵ_r = 0.01 model (which is in the strong feedback limit). In Fig. 10, we plot the maximum accretion in the BH population as a function of the initial metallicity. For most possible combinations of the initial GMC masses and feedback models, there is still no strong dependence on the metallicity. One exception is the 10⁶ M_⊙ GMC with fixed ϵ_r = 0.01, where we see a clear trend in that BH accretion drops as the metallicity increases.

Fig. 10. Impact of the initial metallicity on BH accretion, which is made from a series of simulations in which we vary the initial metallicity (10−6 Z⊙ − Z⊙) and BH radiative-feedback models (fiducial or ϵr = 0.01).

This can be explained with the aid of Figs. 8 and 9. For the 10⁸ M_⊙ GMC, both radiative-feedback models above are in the weak-feedback limit even at the solar metallicity (because the CDF of BH mass accretion is close to that with ϵ_r = 10⁻⁶). However, for the 10⁶ M_⊙ GMC, the ϵ_r = 0.01 model is beginning to move into a “strong” feedback limit as its CDF of mass accretion significantly deviates from the fiducial case. As a result, the GMC metallicity becomes important for that particular case, but in most cases (where ϵ_r ≪ 0.01) the metallicity effects are weak.

3.2.3. Mechanical feedback (jets and winds)

Mechanical feedback is also presented in the second rows of Figs. 8 and 9. For models with fixed mass loading factoring η_w = 1, we again see the trend that the accretion onto black holes is suppressed once the energy efficiency is sufficiently high; this happens at ϵ_w ≳ 10⁻⁵ for both complexes. These “transition points” happen at lower energy than in the radiative feedback simulations. In terms of f_Edd, we find the BHs cannot reach the maximum value once ϵ_w ≈ 1. All these simulations assume the radiative feedback efficiency following Madau et al. (2014); we find the bolometric luminosity decreases when the mechanical feedback is stronger, as expected.

The model from Hu et al. (2022) has variable η_w and ϵ_w. Although its energy efficiency is 10⁻³ − 10⁻² depending on the accretion rate, the accretion rate is highly suppressed: the maximum accretion ($\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$) is even lower than the strong-feedback case with ϵ_w = 0.1. Despite the fact that the energy efficiency is relatively low, the model has a strong momentum outflow that scales as $\dot{P}\ge 0.01f_{\mathrm{Edd}}{\dot{M}}_{\mathrm{Edd}}c$ (see Fig. 2), resulting in very strong BH feedback. Moreover, the fraction of mass flow reaching the BH is low (1/f_Edd in the hyper-Eddington phase), making it relatively difficult for the BH to grow. Instead, a much more significant fraction of the material is ejected as mechanical outflow.

Another important quantity in the mechanical feedback model is the jet-loading factor η_w, which determines the fraction of mass flow that goes into the BH (f_acc = 1/(1 + η_w)). We present the result of this experiment in Fig. 11, where we vary η_w, testing values of 1, 10, and 100, corresponding to f_acc of 0.5, 0.1, and 0.01, while for each variation we keep ϵ_w fixed at the fiducial value of each cloud complex (i.e., change the wind velocity v_w). For both cloud complexes, we find that the fraction of BHs with mass accretion (with the mass resolution of gas) is almost unchanged despite different η_w, while the maximum accreted mass ($\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$) differs. As a rough estimate from constant-ϵ_w models in Fig. 11, $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }\propto 1/\sqrt{{\eta }_{\mathrm{w}}}\approx \sqrt{f_{\mathrm{acc}}}$. We find that this is in agreement with an analytic scaling, which we describe in Sect. 4.

Fig. 11. Effect of jet/wind mass loading factor (ηw) variations, demonstrated with a series of simulations with constant ηw = 1, 10, 100 (but with ϵw fixed at the fiducial value), and the variable model in Hu et al. (2022).

3.2.4. Cosmic rays

Figure 12 shows gas morphology and CR energy density for selected simulations with high CR energy efficiency (a 10⁶ M_⊙ GMC with ϵ_CR = 10⁻³ and a 10⁸ M_⊙ GMC with ϵ_CR = 10⁻²), and zooms onto a rapidly accreting BH. As also suggested in Fig. 3, the BH is located at a dense clump in the GMC. Given the strong CR feedback, there is also strong outflow near the BH. Because of CR feedback, there is a high-energy CR “bubble” near the BH, whose energy density is comparable with CRs generated through stellar feedback. However, these bubbles are of the size of ∼0.25 pc to ∼2.5 pc, significantly smaller than the scale of stellar CRs (typically ∼R_cl). As a result, there is a higher energy (pressure) gradient from the high-energy CR bubbles near the BH, which may then expel gaseous material from the BH or even disrupt the whole GMC.

Fig. 12. Visualization of the GMCs with strong CR feedback, each from a snapshot with rapid BH growth. Left two zoom-in plots: Line-averaged mass density (top) and CR energy density (bottom) near a BH undergoing runaway accretion, based on a 106 M⊙ GMC. We zoom in near the BH, from the left to the right panel, as in Fig. 3. The line-averaged density is evaluated within the box of each panel. We see a high-energy CR bubble generated by the BH. Right two zoom-in plots: Same as the left plots, but embedded in the 108 M⊙ GMC.

From Figs. 8 and 9, we find that BH CR feedback can be important for BH accretion in these dense simulated GMCs if the energy efficiency is high. For example, BH accretion is significantly suppressed when ϵ_CR ≳ 10⁻³ for the 10⁶ M_⊙ GMC, and when ϵ_CR ≳ 10⁻¹ for the 10⁸ M_⊙ GMC. We also see similar trends in f_Edd and L_bol. Despite the fact that CR feedback from SNe is also included in this set of simulations, we find no clear difference when comparing the ϵ_CR = 10⁻⁶ run and the run with fiducial setups (without SN CR feedback), which means this particular stellar feedback mechanism does not bring new effects to BH accretion and feedback.

4. Discussion

4.1. BH feedback and BH accretion

For all the feedback mechanisms simulated here, we see that sufficiently strong BH feedback suppresses BH accretion, as expected. To further quantify the effect of feedback, we show the relationship between the feedback strength (indicated by energy efficiencies ϵ_r, ϵ_w, and ϵ_CR) and the maximum of the accreted mass of the BH population in Fig. 13. In addition to the fixed-value models, we also show some specific subgrid models for reference, in which energy efficiency is estimated at the hyper-Eddington regime (at f_Edd = 1000).

Fig. 13. Dependence of BH accretion on the energy efficiency of specific feedback mechanisms for the 106 M⊙ (top panel) and 108 M⊙ (bottom panel) GMCs. We summarize experiments with fixed-value energy efficiencies (solid) and show the scaling relation (dashed) based on Eq. (4). Several more sophisticated subgrid models are also displayed for reference, and for each of them the energy efficiency is calculated at the hyper-Eddington regime of fEdd = 1000.

For all mechanisms, there is a plateau at the weak-feedback (low energy-efficiency) end, which simply represents the regime where that particular feedback mechanism does not regulate BH growth significantly. However, when feedback is stronger, there is a drop in $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$. We find that this feedback-regulated limit can be approximated with simple analytic arguments at the order-of-magnitude level.

To explain this result, we consider a simple self-regulated model akin to those presented by Silk & Rees (1998), Murray et al. (2005), and Ostriker et al. (2010) for example. First, we consider just radiative and mechanical feedback, because the fiducial model neglects CRs. If accretion is momentum-limited, then BH growth will cease when the “feedback force” 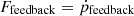$F_{\mathrm{feedback}}={\dot{p}}_{\mathrm{feedback}}$ (momentum injection rate due to feedback) is equal to the gravitational force on gas in the parent complex, F_feedback ∼ F_grav ∼ GM_cl²/R_cl².

For radiative feedback, the radiation pressure is dominated by single scattering (with at most a 𝒪(1) correction from IR multiple scattering) even in our dense clouds, and so ${\dot{p}}_{\mathrm{rad}}\sim L/c\sim {ϵ}_{\mathrm{r}}{\dot{M}}_{\mathrm{BH}}c$. Similarly, for mechanical feedback, ${\dot{p}}_{\mathrm{mech}}\sim {\dot{M}}_w{v}_{\mathrm{w}}\sim \sqrt{2{\eta }_{\mathrm{w}}{ϵ}_{\mathrm{w}}}{\dot{M}}_{\mathrm{BH}}c$.

For CRs, the momentum injection is somewhat less straightforward because it arises via partial confinement and scattering of CRs, generating a CR pressure gradient that accelerates the gas. From the simple analytic, spherically symmetric CR-pressure-driven-wind solutions (Ji et al. 2020; Hopkins et al. 2022), we can approximate this around a dominant point source as ${\dot{p}}_{\mathrm{CR}}\sim {\displaystyle \int d^3}\mathit{x}\widehat{\mathit{r}}·\mathrm{\nabla }{P}_{\mathrm{CR}}\sim {\ell }^2{P}_{\mathrm{CR}}\sim {\dot{E}}_{\mathrm{cr}}/{\overline{v}}_{\mathrm{stream},\mathrm{eff}}$, where ${\dot{E}}_{\mathrm{CR}}\sim {ϵ}_{\mathrm{CR}}{\dot{M}}_{\mathrm{BH}}{c}^2$ and ${\overline{v}}_{\mathrm{stream},\mathrm{eff}}$ is some effective bulk CR streaming speed³ (∼κ/3 ℓ in terms of some characteristic CR gradient scale-length ℓ in the diffusion-dominated regime). Therefore, ${\dot{p}}_{\mathrm{CR}}\sim ({ϵ}_{\mathrm{CR}}\alpha c/{\overline{v}}_{\mathrm{stream},\mathrm{eff}}){\dot{M}}_{\mathrm{BH}}c$, where α collects the order-unity uncertainties in the scalings above. Inserting our assumed κ and assuming ℓ ∼ R_cl, or checking the CR properties in the simulations directly, we see the CRs are not strongly confined, and so the prefactor $\alpha c/{\overline{v}}_{\mathrm{stream},\mathrm{eff}}\sim 10$.

Taking ${\dot{p}}_{\mathrm{feedback}}={\dot{p}}_{\mathrm{rad}}+{\dot{p}}_{\mathrm{mech}}+{\dot{p}}_{\mathrm{CR}}$, we find ${\dot{p}}_{\mathrm{feedback}}\sim ({ϵ}_{\mathrm{r}}+\sqrt{2{\eta }_{\mathrm{w}}{ϵ}_{\mathrm{w}}}+10{ϵ}_{\mathrm{CR}}){\dot{M}}_{\mathrm{BH}}c$. Equating this feedback force to the self-gravity of the cloud complex therefore allows us to determine the maximum possible Ṁ_BH. From Fig. 4, we see that BH growth is dominated by phases with a high accretion rate, which typically reaches f_Edd ∼ 1000. The peak accretion rate can then be parameterized as ${\dot{M}}_{\mathrm{BH}}\sim f_{\mathrm{Edd}}{M}_{\mathrm{BH}}/t_{\mathrm{Sal}}$. We note that $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }\sim M_{\mathrm{BH}}^{\max }$ is reached for the BHs with the most significant mass growth:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }& \sim M_{\mathrm{BH}}^{\max }\sim \frac{G{M}_{\mathrm{cl}}^2}{R_{\mathrm{cl}}^2}\frac{t_{\mathrm{Sal}}}{f_{\mathrm{Edd}}c}\frac{1}{{ϵ}_{\mathrm{r}}+\sqrt{2{\eta }_{\mathrm{w}}{ϵ}_{\mathrm{w}}}+10{ϵ}_{\mathrm{CR}}}\hfill \\ \hfill & \sim 3\times {10}^4{\mathrm{M}}_{\odot }{\left(\frac{M_{\mathrm{cl}}}{{10}^6{\mathrm{M}}_{\odot }}\right)}^2{\left(\frac{R_{\mathrm{cl}}}{5\mathrm{pc}}\right)}^{-2}\hfill \\ \hfill & \times \frac{1}{f_{\mathrm{Edd}}({ϵ}_{\mathrm{r}}+\sqrt{2{\eta }_{\mathrm{w}}{ϵ}_{\mathrm{w}}}+10{ϵ}_{\mathrm{CR}})}·\hfill \end{array}$$(4)

With Eq. (4), we plot the scaling relations for each feedback mechanism variation in Fig. 13. First, we check models varying radiative and mechanical feedback efficiency, that is, ϵ_CR = 0. As described above, for the fiducial mechanical feedback model, we input ϵ_w = 10⁻⁶ for the 10⁶ M_⊙ complex and ϵ_w = 10⁻³ for the 10⁸ M_⊙ one; for the fiducial radiative feedback, we input ϵ_r = 3 × 10⁻³ (cf. Fig. 2) because f_Edd = 1000 is reached. Varying the feedback efficiency, we find both scaling relations for the radiative and mechanical feedback are in good agreement with the simulations.

Considering CRs, we also find the scaling relation agrees quite well with the simulations, though from our analytic scaling, we see that this is more sensitive to uncertainties on CR transport physics than it is to those on ϵ_CR. It remains highly theoretically uncertain as to how well-coupled GeV CRs are in dense, neutral-phase ISM gas (see e.g., Zweibel 2017; Krumholz et al. 2020; Hopkins et al. 2021), and the CR transport model we adopt is purely phenomenological, which means the details of this scaling should be taken with great caution; nonetheless, it provides some order-of-magnitude guidance.

4.2. BH feedback and star formation

Figure 14 shows the star formation efficiency (SFE; here defined as the ratio between the stellar mass at the end of the simulation and the initial total gas mass) for different kinds of feedback mechanisms and various energy efficiencies. When the energy efficiency is sufficiently low, we find that in both the 10⁶ M_⊙ and 10⁸ M_⊙ GMCs, the SFE is ∼0.3. This is expected because the two GMCs have the same initial mean surface density (Grudić et al. 2018, and more citations in Sect. 1). Then, once the energy efficiency increase beyond ∼10⁻³, the SFE for the 10⁶ M_⊙ GMC drops below 0.1. However, the impact on the 10⁸ M_⊙ is not significant.

Fig. 14. Star formation efficiency in our experiments with various fixed-value BH-feedback energy efficiencies. For the 106 M⊙ GMC, there is (sometimes extreme) suppression of the SFE at high energy efficiency.

A very special case is the ϵ_CR = 0.1 run, in which the SFE drops to a very low value (< 10⁻³). Upon further inspection of the run, we find that the cloud was disrupted by strong CR winds at ∼0.3 t_ff, which is much shorter than the characteristic timescale of star formation at the low-BH-feedback limit (from simulations, it is $t_{1/2}^{\mathrm{SF}}\sim 1.25t_{\mathrm{ff}}$, defined as the time when the SFE reaches half of the final value). As a result, the SFE almost freezes at the (extremely low ) star-formation level at the time of GMC disruption.

We may roughly explain this quantitatively. From our simulations, a typical BH growth history is dominated by a few “bursty” super-Eddington accretions that take place over a short period of time (typically less than 0.05 t_ff). On a much longer timescale than the bursty growth, the BH mass is then anticipated to reach $M_{\mathrm{BH}}\sim M_{\mathrm{BH}}^{\mathrm{ini}}exp(⟨f_{\mathrm{Edd}}⟩t/t_{\mathrm{Sal}})$ Applying this to the BH with the most significant mass growth, we find the disruption time of the GMC due to strong BH feedback to be

$$\begin{array}{c}\hfill t_{\mathrm{d}}\sim \frac{t_{\mathrm{Sal}}}{⟨f_{\mathrm{Edd}}⟩}ln(1+\frac{\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }}{M_{\mathrm{BH}}^{\mathrm{ini}}})·\end{array}$$(5)

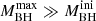For each simulation, $M_{\mathrm{BH}}^{\max }$ and ⟨f_Edd⟩ are presented in the middle columns of Figs. 5, 8, and 9; and $M_{\mathrm{BH}}^{\max }$ (or $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$) is also analytically evaluated from Eq. (4). In general, we find that ⟨f_Edd⟩ is approximately 10−100, and there is $M_{\mathrm{BH}}^{\max }\gg M_{\mathrm{BH}}^{\mathrm{ini}}$, and so t_d is generally much larger than the free-fall time of the two GMCs we simulated. However, when there is very strong BH feedback, $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$ is low, and so there may be situations where $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }\ll M_{\mathrm{BH}}^{\mathrm{ini}}$ and $t_{\mathrm{d}}\sim t_{\mathrm{Sal}}\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }/(⟨f_{\mathrm{Edd}}⟩M_{\mathrm{BH}}^{\mathrm{ini}})$ is smaller than (or comparable with) the free-fall time. For the ϵ_CR = 0.1 run of the 10⁶ M_⊙ complex, we measure and find $M_{\mathrm{BH}}^{\mathrm{ini}}=702$ M_⊙ and $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }=740$ M_⊙ (thus $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }/M_{\mathrm{BH}}^{\mathrm{ini}}\approx 0.05$), resulting in t_d ∼ 2/⟨f_Edd⟩ Myr. The timescale is comparable to the free-fall time of the GMC (0.19 Myr), or could be substantially smaller if ⟨f_Edd⟩ were large.

We also note that the above argument on the disruption of the GMC by BH feedback is dependent on the initial mass of the BH, and thus t_d is essentially short only when the “lucky” seed BH is initially massive. As a result, the extreme suppression of SFE does not always take place, even if the energy efficiency is high, which is true for most experiments in Fig. 14 with high energy efficiency.

In summary, we find that BH feedback will not affect the SFE unless it is in a highly feedback-dominated or feedback-regulated regime and a relatively low-mass cloud complex with high-mass “active” seeds (M_BH ≳ 10³ M_⊙ with ϵ ≳ 10⁻³ for the 10⁶ M_⊙ GMC). The significance of the impact is largely decided by how soon the winds induced by BH feedback “interrupt” star formation (which takes place on the free-fall timescale) – in some particular models (e.g., very strong feedback from a massive BH seed), even if BH accretion is limited, the strong BH feedback is still able to disrupt the whole GMC at a very early stage in the star-formation history, resulting in very low SFE.

4.3. Caveats and outlook

Because of the huge mismatch in scales of the BH accretion and feedback problem (from kpc and pc scales to the Schwarzschild radius), it is difficult to simulate every aspect of these processes in great detail. In this study, we concentrate on larger scales, where the gas inflow towards the gravitational capture radii of the BHs is resolved, but the dynamics of the small scales (gas cells that are considered “gravitationally bound to the BH”, including the accretion disks themselves) are described by subgrid models with a few free parameters (as listed in Table 2). However, the setup is sufficient to answer the question we are asking, which pertains to whether there could be sufficient fuel from large scales (kpc/pc) reaching small scales (subpc) to power rapid BH growth in the presence of BH feedback. With our setup, we are therefore also able to study the impact of different subgrid parameters on BH accretion, in an attempt to bridge the dynamics of small and large scales.

Still, the subgrid models and resolution of our simulations do not allow us to connect the large and small scales with great self-consistency. For example, the energy efficiencies of different feedback mechanisms are treated as arbitrary inputs, which are not dependent on BH ambient boundary conditions, such as magnetic field and angular momentum flow. There is therefore plenty of room for improvement.

Recent zoom-in simulations of BH accretion or feedback may shed light on this problem (e.g., Talbot et al. 2021; Guo et al. 2023; Hopkins et al. 2024a,b). With the technique of super-Lagrangian refinement, small-scale structures (e.g., BH accretion disks or jets) and dynamics (e.g., the magnetic field in disks, jet launching mechanisms, BH–disk interactions) may also be simulated with a higher level of self-consistency.

Finally, as also described in Paper I, next-generation simulations that resolve individual stars (Grudić et al. 2021a; Guszejnov et al. 2021) may enable other important processes, such as BH seed formation, stellar merging, and BH accretion/feedback in the same simulation.

Fig. 15. Overview of seed BH accretion and feedback in star-forming GMCs. (a) Initial condition, where the seed BH is inside a turbulent, pre-star-formation GMC. (b) Scenario where the self-gravity of the GMC (characterized by its mean surface density), star formation, and feedback dominate and disrupt the GMC, suppressing BH accretion. (c) Scenario where the GMC’s self-gravity is strong and gas is kept bound, creating a proper environment for BH accretion and feedback. (d) Scenario where the BH feedback is weak, and there is steady accretion flow towards the BH if it is at the center of the potential well. (e), (f), and (g) Strong feedback in different forms may suppress both BH accretion and star formation; this process is dominated by momentum outflow from BHs and can be approximated with the analytic argument as in Eq. (4).

5. Conclusions

This study is a parameter-space survey of seed BH accretion and feedback in star-forming GMCs, with key parameters listed in Table 2. We focus on high-surface-density clouds, which are ideal environments for runaway BH accretion in the weak BH feedback limit (Paper I), and find that BH feedback self-regulates BH growth. Our major conclusions are listed below and illustrated in Fig. 15.

• Even with feedback, the BH accretion scenario is the same as that presented in Paper I. Rapid BH accretion happens when BHs semi-randomly encounter dense gas clumps with low relative velocities. This only occurs when the dynamics of both BH and gas are dominated by the self-gravity of the GMC; that is, when the cloud has sufficient surface density that stellar feedback is inefficient, and the BH has low enough mass that BH feedback is (initially) weak. Other GMC properties, such as metallicity, have weak effects (except in some models with strong radiative feedback). Also, as in the condition without BH feedback (Paper I), initial information about BHs, such as initial mass, position, and velocity, does not significantly correlate with BH accretion (as long as BHs are initially gravitationally bound to the GMC), meaning there is significant stochasticity in the process.

• With our fiducial feedback model (“log-form” radiative efficiency and “critical” mechanical feedback efficiency), we find there is suppression of BH accretion in both simulations with 10⁶ M_⊙ and 10⁸ M_⊙ GMCs. Significant BH accretion is more likely in the 10⁸ M_⊙ GMC, as expected, where BHs grow up to ∼5 × 10⁴ M_⊙, even though we assume relatively efficient radiative ⟨ϵ_r⟩∼0.003 and ⟨ϵ_w⟩∼0.001 (so ⟨ϵ_w⟩/⟨ϵ_r⟩∼1/3). There are short phases of hyper-Eddington accretion (f_Edd ∼ 1000) for both simulations.

• For feedback physics involved in this study, we find that the maximum possible accreted mass for BHs $\mathrm{\Delta }{M}_{\mathrm{BH}}^{\max }$ declines as the feedback efficiency increases (Fig. 13), in a manner consistent with momentum-regulated BH growth. The simulations agree well with a simple analytic scaling, as summarized in Eq. (4). Depending on the cloud’s properties and the feedback efficiency, the scenario can produce 10⁴ M_⊙ IMBHs quickly in a few free-fall times (typically ∼1 Myr). These IMBHs can be the “massive seeds” of subsequent galactic SMBHs.

• For a given feedback efficiency model, the amount by which BHs can grow increases both with the surface density–acceleration scale of the parent complex and the gas mass available. Therefore, massive dense environments, such as high-redshift galaxy nuclei, will (unsurprisingly) be most favorable to rapid IMBH and even SMBH-level growth. Owing to the different physical mechanisms by which energy is converted into momentum, the same “energetic” efficiency ϵ for different physical mechanisms (radiation, mechanical outflows, cosmic rays) will not produce the same level of self regulation (Eq. 4). Physically motivated models with variable radiative efficiency ϵ_r (e.g., Watarai et al. 2000; Madau et al. 2014) tend to predict relatively low ϵ_r at high Eddington ratios, and so it seems unlikely that this is actually the dominant self-regulation mechanism on the scales resolved here. In contrast, some recent models for broad-opening angle, nonrelativistic winds from super-Eddington disks (Hu et al. 2022) suggest that this efficiently produces momentum-loaded winds with large (η_w ≫ 1) mass loading, which would expel most of the gravitationally captured mass before it can reach the BH, and would much more efficiently suppress BH growth in the simulations presented here.

• Even when BH accretion overall is suppressed by BH feedback with high efficiency, there are still short phases of very high accretion rate ($\gtrsim 100{\dot{M}}_{\mathrm{Edd}}$) for a subset of BHs in the simulation (∼10% for the 10⁶ M_⊙ GMC and ∼1% for the 10⁸ M_⊙ one).

• When varying the BH feedback efficiency, we find that the global SFE of the massive complex is generally not suppressed by BH feedback, unless the BH feedback efficiency is very high (≳0.01), such that the cloud complex is disrupted quickly before the free-fall time.

• Other parameters are related to the subgrid (unresolved) mass flow to the BH; that is, the effective α, the upper limit on BH accretion rate, and the jet mass-loading factor η_w are largely degenerate, but do affect the BH mass growth (as expected by definition in our models).

Some of these findings are similar to other recent works. For example, Lupi et al. (2016) simulated the super-critical accretion onto stellar-mass BH seeds in gaseous circumnuclear disks, with constant ϵ_r = 0.1 or the slim disk model (Madau et al. 2014) for radiative efficiency. Pezzulli et al. (2016) studied the growth of the central BH (initially with ∼100 M_⊙ seed mass) of high-redshift quasars with a semi-analytic framework, including the slim-disk model and AGN wind feedback efficiency of ∼10⁻³ (but not CRs). Our results are similar to theirs for simulations with similar feedback parameters.

Extension of this work may include more sophisticated subgrid models of BH accretion, which connect the BH accretion with the properties of the ambient gas. Another direction is to develop zoom-in simulations that attain higher resolution near the BH seed, which is more self-consistent but computationally more expensive. We leave these possibilities for future work.

Acknowledgments

Support for the authors was provided by NSF Research Grants 1911233, 20009234, 2108318, NSF CAREER grant 1455342, NASA grants 80NSSC18K0562, HST-AR15800. Numerical calculations were run on the Caltech compute cluster “Wheeler”, allocations AST21010 and AST20016 supported by the NSF and TACC, and NASA HEC SMD-16-7592. A public version of the GIZMO code is available at http://www.tapir.caltech.edu/~phopkins/Site/GIZMO.html. YS acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), [funding reference number 568580].

References

All Tables

All Figures

Fig. 1. Mass and energy flow of BH accretion and feedback. This study extends the framework of star formation in Grudić et al. (2018) and BH accretion without feedback in Paper I. To implement BH feedback, we use a model of mass transfer from the disk to the BH. With only a fraction of the accretion flow going to the BH, other portions are deposited back to the GMC in the form of radiation, jets and winds, and cosmic rays. We note that since the feedback energy efficiencies are typically small (≲0.1), ${\dot{M}}_{\mathrm{BH}}\doteq {\dot{M}}_{\mathrm{BH},0}$.

In the text

Fig. 2. Subgrid models for radiative feedback (top panel) and mechanical feedback (bottom two panels). Top: Energy- and momentum-ejection rates as a function of accretion rates, including “log-form” models inferred from the slim disk (solid), and simple ones with constant ${ϵ}_{\mathrm{r}}\equiv L/({\dot{M}}_{\mathrm{BH}}{c}^2)$ (dashed). Bottom: Momentum-ejection rates for mechanical feedback with constant ${ϵ}_{\mathrm{w}}\equiv {\dot{E}}_{\mathrm{kin}}/({\dot{M}}_{\mathrm{BH}}{c}^2)$ (dashed), and the model in Hu et al. (2022) – though the released kinetic energy is almost constant ($E_{\mathrm{kin}}\approx 4\times {10}^{-4}{\dot{M}}_{\mathrm{Edd}}{c}^2$), the momentum-injection rate grows linearly ($\dot{p}\approx 0.03f_{\mathrm{Edd}}{\dot{M}}_{\mathrm{Edd}}c$) because of the variable mass-loading factor.

In the text

Fig. 3. Visualization of simulations with and without BH feedback physics, each from a snapshot when a BH is undergoing rapid growth. Left two zoom-in plots: Gas morphology for the 106 M⊙ GMCs without (top) or with (bottom) BH feedback. From left to right, we zoom into a BH undergoing hyper-Eddington accretion. As the smallest scale, each panel shows the velocity field near the BH, with the circular velocity ($\sqrt{G{M}_{\mathrm{cl}}/R_{\mathrm{cl}}}$) presented as a gauge. Right two zoom-in plots: Same as the left plots, but for the 108 M⊙ GMC.

In the text

Fig. 4. Mass evolution and accretion rate for BH particles in different GMCs. In the first and third panels (from top to bottom), we select five BHs with significant mass growth from high-resolution simulations of the two complexes and plot the evolution of the mass bound to the BH (BH+disk, solid) and the BH-only mass (dashed). In the second and fourth panels, we show the accretion rate for the same BHs, each rescaled to its Eddington accretion rate ($f_{\mathrm{Edd}}={\dot{M}}_{\mathrm{BH}}/{\dot{M}}_{\mathrm{Edd}}$).

In the text

Fig. 5. Cumulative distribution function of the accreted mass, Eddington ratio, and bolometric luminosity for BH populations in simulations with the fiducial BH feedback setups. In the right two panels, we show the distribution of the “peak” value throughout the evolution. Both the high- (solid) and low-resolution (dashed) simulations are displayed and show qualitatively similar trends. The artificial flat “plateau” at the left of some lines reflects the mass-resolution limit of that simulation.

In the text

Fig. 6. Dependence of BH accretion on initial conditions of BHs. From our high-resolution fiducial simulations, we mark BHs with resolved accretion in a phase space of the accreted mass (ΔMBH) versus the initial mass ($M_{\mathrm{BH}}^{\mathrm{ini}}$), distance to the cloud’s center ($r_{\mathrm{BH}}^{\mathrm{ini}}$), velocity ($v_{\mathrm{BH}}^{\mathrm{ini}}$), and specific angular momentum ($j_{\mathrm{BH}}^{\mathrm{ini}}$). We find only a weak dependence on these initial conditions. We may also clearly see the mass-resolution limit from the lower “cutoff” in ΔMBH for the 108 M⊙ complex.

In the text

	Fig. 7. Parameter survey of the accretion model, using an effective α-parameter to quantify the accretion rate. Here we vary α and the upper limit on disk mass. In the fiducial case (dashed), α = 0.1 and Md/MBH ≤ 10.
In the text

Fig. 8. Parameter survey of the energy efficiency in different feedback mechanisms based on experiments with the 106 M⊙ complex. From left to right, the three columns show the CDF of accreted mass by BHs, as well as the highest possible fEdd and Lbol throughout the evolution. Each row represents a set of simulations with varying models of a specific feedback mechanism (labeled in each left panel), with the fiducial model marked in black dashed lines.

In the text

	Fig. 9. Parameter survey of the energy efficiency in different feedback mechanisms based on experiments with the 108 M⊙ cloud complex. Conventions are the same as those in Fig. 8.
In the text

	Fig. 10. Impact of the initial metallicity on BH accretion, which is made from a series of simulations in which we vary the initial metallicity (10−6 Z⊙ − Z⊙) and BH radiative-feedback models (fiducial or ϵr = 0.01).
In the text

	Fig. 11. Effect of jet/wind mass loading factor (ηw) variations, demonstrated with a series of simulations with constant ηw = 1, 10, 100 (but with ϵw fixed at the fiducial value), and the variable model in Hu et al. (2022).
In the text

Fig. 12. Visualization of the GMCs with strong CR feedback, each from a snapshot with rapid BH growth. Left two zoom-in plots: Line-averaged mass density (top) and CR energy density (bottom) near a BH undergoing runaway accretion, based on a 106 M⊙ GMC. We zoom in near the BH, from the left to the right panel, as in Fig. 3. The line-averaged density is evaluated within the box of each panel. We see a high-energy CR bubble generated by the BH. Right two zoom-in plots: Same as the left plots, but embedded in the 108 M⊙ GMC.

In the text

Fig. 13. Dependence of BH accretion on the energy efficiency of specific feedback mechanisms for the 106 M⊙ (top panel) and 108 M⊙ (bottom panel) GMCs. We summarize experiments with fixed-value energy efficiencies (solid) and show the scaling relation (dashed) based on Eq. (4). Several more sophisticated subgrid models are also displayed for reference, and for each of them the energy efficiency is calculated at the hyper-Eddington regime of fEdd = 1000.

In the text

	Fig. 14. Star formation efficiency in our experiments with various fixed-value BH-feedback energy efficiencies. For the 106 M⊙ GMC, there is (sometimes extreme) suppression of the SFE at high energy efficiency.
In the text

Fig. 15. Overview of seed BH accretion and feedback in star-forming GMCs. (a) Initial condition, where the seed BH is inside a turbulent, pre-star-formation GMC. (b) Scenario where the self-gravity of the GMC (characterized by its mean surface density), star formation, and feedback dominate and disrupt the GMC, suppressing BH accretion. (c) Scenario where the GMC’s self-gravity is strong and gas is kept bound, creating a proper environment for BH accretion and feedback. (d) Scenario where the BH feedback is weak, and there is steady accretion flow towards the BH if it is at the center of the potential well. (e), (f), and (g) Strong feedback in different forms may suppress both BH accretion and star formation; this process is dominated by momentum outflow from BHs and can be approximated with the analytic argument as in Eq. (4).

In the text