| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 32 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202243110 | |
| Published online | 09 September 2022 | |
Scaling relations of z ∼ 0.25–1.5 galaxies in various environments from the morpho-kinematics analysis of the MAGIC sample⋆,⋆⋆,⋆⋆⋆
1
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse, CNRS, UPS, CNES, 31400 Toulouse, France
e-mail: wilfried.mercier@irap.omp.eu
2
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
3
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
4
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
5
Univ. Lyon, Univ. Lyon1, Ens de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval, France
6
Escuela de Fisica, Universidad Industrial de Santander, A.A. 678, Bucaramanga, Colombia
7
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
8
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
9
Canada-France-Hawaii Telescope, CNRS, 96743 Kamuela, HI, USA
Received:
14
January
2022
Accepted:
14
April
2022
Context. The evolution of galaxies is influenced by many physical processes, which may vary depending on their environment.
Aims. We combine Hubble Space Telescope (HST) and Multi-Unit Spectroscopic Explorer (MUSE) data of galaxies at 0.25 ≲ z ≲ 1.5 to probe the impact of environment on the size-mass relation, the main sequence (MS) relation, and the Tully-Fisher relation (TFR).
Methods. We perform a morpho-kinematics modelling of 593 [O II] emitters in various environments in the COSMOS area from the MUSE-gAlaxy Groups In Cosmos survey. The HST F814W images are modelled with a bulge-disk decomposition to estimate their bulge-disk ratio, effective radius, and disk inclination. We use the [O II]λλ3727, 3729 doublet to extract the galaxies’ ionised gas kinematics maps from the MUSE cubes, and we model those maps for a sample of 146 [O II] emitters, including bulge and disk components constrained from morphology and a dark matter halo.
Results. We find an offset of 0.03 dex (1σ significant) on the size-mass relation zero point between the field and the large structure sub-samples, with a richness threshold of N = 10 to separate between small and large structures, and of 0.06 dex (2σ) with N = 20. Similarly, we find a 0.1 dex (2σ) difference on the MS relation with N = 10 and 0.15 dex (3σ) with N = 20. These results suggest that galaxies in massive structures are smaller by 14% and have star formation rates reduced by a factor of 1.3 − 1.5 with respect to field galaxies at z ≈ 0.7. Finally, we do not find any impact of the environment on the TFR, except when using N = 20 with an offset of 0.04 dex (1σ). We discard the effect of quenching for the largest structures, which would lead to an offset in the opposite direction. We find that, at z ≈ 0.7, if quenching impacts the mass budget of galaxies in structures, these galaxies would have been affected quite recently and for roughly 0.7 − 1.5 Gyr. This result holds when including the gas mass but vanishes once we include the asymmetric drift correction.
Key words: galaxies: evolution / galaxies: kinematics and dynamics / galaxies: clusters: general / galaxies: groups: general / galaxies: high-redshift
Full Appendix G is available at https://www.aanda.org
Full Table F.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/665/A54
© W. Mercier et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The evolution of galaxies is not a trivial process, as numerous physical mechanisms that act on different physical scales and timescales and with different amplitudes are at play. From an observational point of view, our understanding of galaxy evolution has greatly improved over roughly the last 25 years thanks to: (i) extended multi-band imaging and spectroscopic surveys of the local Universe (e.g., SDSS and 2dFGRS); (ii) the advent of the Hubble Space Telescope (HST), associated with 8–10 m class telescopes (e.g., VLT and Keck), which allowed galaxies in the more distant Universe to be probed and studied by combining extremely deep images (e.g., HUDF and COSMOS) with large spectroscopic surveys (e.g., VVDS and zCOSMOS); and (iii) the development and continuous improvement of 3D spectrographs (e.g., SINFONI, KMOS, and MUSE), whose data have allowed distant galaxies be to studied in even more detail. The current paradigm for galaxy evolution is that galaxies must have first formed their dark matter (DM) haloes in the early stages of the Universe, and only later started assembling their baryonic mass, by continuous accretion via the circumgalactic medium of mainly cold gas from filaments located in the cosmic web (e.g., Kereš et al. 2005; Ocvirk et al. 2008; Bouché et al. 2013; Zabl et al. 2019), by galactic wind recycling (Davé 2009; Hopkins et al. 2012; Schroetter et al. 2019), or through galaxy mergers (López-Sanjuan et al. 2012; Ventou et al. 2017, 2019; Mantha et al. 2018; Duncan et al. 2019). In particular, this scenario is favoured to explain the high star formation rates (SFRs) measured in the past billion years, which would have rapidly depleted the galaxies’ gas content and would have led the galaxies to an early quenching phase unless their gas reservoir was continuously replenished throughout cosmic time. Thus, the mass assembly of the baryonic components of galaxies must be tightly linked to the evolution of their DM content.
This picture is further supported by the fact that high redshift galaxies appear to be quite different from their local counterparts, indicative that they must have radically evolved in order to populate the Hubble sequence that we see today. Studies comparing the global properties of high and low redshift galaxies have indeed shown that the former tend to be on average smaller (Trujillo et al. 2007; van der Wel et al. 2014b; Mowla et al. 2019) and less massive (Ilbert et al. 2010; Muzzin et al. 2013) than the latter. At the same time, galaxies have shown a rise in their mean SFR throughout cosmic time up to a peak of star formation at redshift z ∼ 2 before declining to the typical value of roughly 0.01 M⊙ yr−1 Mpc−3 measured today (Hopkins & Beacom 2006), and their molecular gas fraction is also found to be larger at high redshift (Tacconi et al. 2018; Freundlich et al. 2019; Walter et al. 2020). In addition to their global properties, galaxies also show clear signs of morphological and kinematics evolution. Several studies have highlighted the fact that the proportion of triaxial systems and thick disks increases as we go to higher redshifts, with low mass galaxies having a larger tendency to be triaxial (van der Wel et al. 2014a; Zhang et al. 2019). This would suggest a trend for star-forming galaxies to flatten as they evolve, going from prolate to oblate shapes. At the same time, intermediate to high redshift galaxies are found to have on average more complex and perturbed gas kinematics with a larger velocity dispersion than their local counterparts (Flores et al. 2006; Yang et al. 2008; Epinat et al. 2010). While understanding the evolution of the different galaxy populations down to the intricate details is a particularly tedious task, it has become clear that there must exist a finite set of physical mechanisms at play that drives the bulk of the evolution in order to explain the various scaling relations first discovered in the local Universe but which have been shown to hold at intermediate and high redshift. Among these we can cite the Schmidt-Kennicutt relation (e.g., Schmidt 1959; Kennicutt 1998a), the mass-size relation (e.g., Shen et al. 2003; Mowla et al. 2019), the main sequence (MS) relation (e.g., Noeske et al. 2007; Whitaker et al. 2014), the Tully-Fisher relation (TFR; e.g., Tully & Fisher 1977; Contini et al. 2016; Tiley et al. 2019; Abril-Melgarejo et al. 2021), and the mass-metallicity relation (e.g., Tremonti et al. 2004; Erb et al. 2006).
One key question is whether the transition seen from high to low redshift between morphologically disturbed, particularly active galaxies to mostly relaxed, massive low-star-formation systems is mainly driven by in situ physical phenomena such as supernova-driven galactic super winds and active galactic nucleus feedback or, on the contrary, is driven by the environment within which these galaxies lie. This question has led discussions about the impact of galaxy clusters to the physical properties, morphology, and kinematics of their constituent galaxies. The two main mechanisms that can affect star formation in galaxies located in clusters with respect to those in the lowest-density environments (hereafter ‘field’ galaxies) are bursts of star formation and quenching (e.g., see Peng et al. 2010, for an analysis of environment and mass quenching in the local Universe). While the latter is not specifically inherent to galaxy clusters, these massive structures tend to accelerate its effect either through hydrodynamical mechanisms, such as ram-pressure stripping (e.g., Gunn & Gott 1972; Boselli et al. 2019) and thermal evaporation (e.g., Cowie & McKee 1977; Cowie & Songaila 1977), or through gravitational mechanisms, such as galaxy harassment (e.g., Cortese et al. 2021).
Until quite recently, few studies had tried to investigate the well-known scaling relations as a function of the environment of galaxies, except for the MS relation. Indeed, the MS relation is probably one of the most studied scaling relations as a function of environment as it can be used to directly probe the impact of quenching on the evolution of galaxies. Following the recent data release announcement of the Gemini Observations of Galaxies in Rich Early ENvironments (GOGREEN) and Gemini CLuster Astrophysics Spectroscopic Survey (GCLASS) surveys (Balogh et al. 2020), aimed at probing the impact of dense environments on intermediate redshift (0.8 < z < 1.5) galaxy properties, Old et al. (2020a,b) explored the environmental dependence of the star-forming MS between massive clusters and field galaxies. Using the [O II] doublet flux as a proxy for the SFR, they found the SFR of cluster galaxies to be on average 1.4 times lower than that of their field sample, the difference being more pronounced for low stellar masses. Alternatively, Erfanianfar et al. (2016), using data from the Cosmic Evolution Survey (COSMOS), All-Wavelength Extended Groth Strip International Survey (AEGIS), Extended Chandra Deep Field-South (ECDFS), and Chandra Deep Field North (CDFN) fields, could not find any difference in the MS relation between field galaxies and those in structures in the redshift range 0.5 < z < 1.1, but they did find a similar trend to that of Old et al. (2020b) in the lowest redshift regime (0.15 < z < 0.5). On the other hand, Nantais et al. (2020) could not find any significant difference between field and Spitzer Adaptation of the Red-Sequence Cluster Survey (SpARCS; Muzzin et al. 2009) cluster galaxies at redshift z ∼ 1.6, which, according to the authors, could be explained either by the fact that galaxies might have been accreted too recently to show signs of quenching or by the fact that the clusters might be not mature enough yet at this redshift to produce measurable environmental effects on these galaxies.
The environmental impact on the size-mass relation began to be studied only in the last decade, by Maltby et al. (2010). Using galaxies from the Space Telescope A901/2 Galaxy Evolution Survey (STAGES) survey (Gray et al. 2009), they found no difference in the size-mass relation for massive galaxies (M⋆ > 1010 M⊙) and a significant offset for intermediate to low mass galaxies, consistent with field spiral galaxies being about 15% larger than those in clusters at z ∼ 0.16. Alternatively, Kuchner et al. (2017) found a similar relation at high mass rather than at low mass for late-type galaxies at z = 0.44, where cluster galaxies were smaller than their field counterparts, and Matharu et al. (2019) found the same trend when comparing the size-mass relation between field and cluster galaxies at z ∼ 1. However, Kelkar et al. (2015), using data from the ESO Distant Cluster Survey, could not find any difference between field and cluster galaxies in the redshift range 0.4 < z < 0.8.
Finally, regarding the TFR, Pelliccia et al. (2019) searched for differences between two samples of galaxies in groups and clusters from the Observations of Redshift Evolution in Large-Scale Environments (ORELSE) sample (Lubin et al. 2009) using long-slit spectroscopy data to derive the galaxies’ kinematics. They could not find any significant difference between the two TFRs and therefore claimed the environment had no impact. More recently, Abril-Melgarejo et al. (2021) analysed a sample of z ∼ 0.7 galaxies located in galaxy groups from the MUSE-gAlaxy Groups In Cosmos (MAGIC) survey (Epinat et al., in prep.) using Multi-Unit Spectroscopic Explorer (MUSE) and HST data. By comparing their TFR with that from the K-band Multi Object Spectrograph 3D (KMOS3D; Úbler et al. 2017), KMOS Redshift One Survey (KROSS; Tiley et al. 2019), and ORELSE (Pelliccia et al. 2019) samples, they found a significant offset in the TFR zero point, which they attributed to a possible impact of the environment since these samples targeted different populations of galaxies (galaxies in groups and clusters versus galaxies in clusters and in the field). This result led them to two different interpretations of this offset:
-
(i)
A quenching of star formation visible in the massive structures that led to a decrease in stellar mass with respect to the field or
-
(ii)
A baryon contraction phase for the galaxies in groups and clusters that led to an increase in circular velocity for these galaxies.
However, they also indicated that comparing samples from different datasets, with physical quantities derived from different tools, methods, and models and with different selection functions, leads to many uncertainties that might compromise the interpretation. Thus, they argued that, in order to study the impact of the environment on the TFR in a robust way, one would need to self-consistently apply the same methodology and models to galaxies located in various environments (field, groups, and clusters), which is the goal of this paper.
Here we push beyond the previous analysis performed by Abril-Melgarejo et al. (2021) and investigate differences in three main scaling relations (size-mass, MS, and TFR) when using samples that target different environments, with HST and MUSE data from the MAGIC survey. Because this survey targets galaxies located in galaxy groups and clusters, as well as foreground and background galaxies in a similar redshift range without prior selection, we expect to probe the impact of the environment on these relations in detail and with reduced uncertainties by applying the same procedure to model the morphology with HST images and the kinematics with MUSE cubes using the [O II] doublet.
This paper is structured as follows. In Sect. 2 we present the HST and MUSE data. In Sect. 3 we introduce the initial MAGIC sample and the structure identification, and we explain how we derived the galaxies’ global properties (stellar mass and SFR). In Sect. 4 we present the morphological modelling performed with GALFIT on the entire [O II] emitter sample with reliable redshifts, the aperture correction applied for the stellar mass, and the prescription we applied to derive an average disk thickness as a function of redshift. In Sect. 5 we describe the kinematics modelling using the [O II] doublet as a kinematics tracer, as well as the mass models used to constrain the kinematics from the stellar distribution. In Sect. 6 we discuss the selection criteria applied to select samples to study the size-mass relation, the MS relation, and the TFR. Finally, we focus in Sect. 7 on the analysis of the three scaling relations as a function of environment. Throughout the paper we assume a Λ cold dark matter cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
2. MUSE and HST data
2.1. MUSE observations and data reduction
Galaxies studied in this paper are part of the MAGIC survey. This survey targeted 14 galaxy groups located in the COSMOS area (Scoville et al. 2007b) selected from the COSMOS group catalogue of Knobel et al. (2012) in the redshift range 0.5 < z < 0.8, and observed during Guaranteed Time Observations as part of an observing programme studying the effect of the environment on 8 Gyr of galaxy evolution (PI: T. Contini). Though more details will be given in the MAGIC survey paper (Epinat et al., in prep), we provide in what follows a summary of the data acquisition and reduction.
In total, 17 different MUSE fields were observed over seven periods. For each target, observing blocks (OBs) of four 900-s exposures were combined, including a small dithering pattern, as well as a rotation of the field of 90° between each exposure. The final combined data cubes have total exposure times ranging between 1 and 10 hours. Because kinematics studies are quite sensitive to spatial resolution, we required observations to be carried out under good seeing conditions with a point spread function (PSF) full width at half maximum (FWHM) lower than 0.8″, except in cases where the adaptive optics (AO) system was used.
The MUSE standard pipeline (Weilbacher et al. 2020) was used for the data reduction on each OB individually. Observations with AO used the v2.4 version, whereas the others used v1.6, except for the MUSE observations of COSMOS group CGr30, which used v1.2. Default sky subtraction was applied on each science exposure before aligning and combining them using stars located in the field. To improve sky subtraction, the Zurich Atmosphere Purge software (Soto et al. 2016) was then applied onto the final combined data cube. The reduction leads to data and variance cubes with spatial and spectral sampling of 0.2″ and 1.25 Å, respectively, in the spectral range 4750 − 9350 Å.
As shall be discussed in more detail in Sect. 5, the kinematics maps, which are extracted from the MUSE data cubes, serve as a basis for the kinematics modelling. Among those kinematics maps are the ionised gas velocity field and velocity dispersion maps, which are highly affected by both the limited spectral (line spread function) and spatial (PSF) resolutions of MUSE data through beam smearing. Because extracting reliable kinematics parameters depends on correctly taking into account the impact of the beam smearing in the kinematics models of the galaxies, it is therefore important to know the values of the MUSE PSF and line spread function (LSF) FWHM at the wavelength of observation. The MUSE LSF is modelled using the prescription from Bacon et al. (2017) and Guérou et al. (2017) who derived the wavelength dependence of the MUSE LSF FWHM in the Hubble Ultra Deep Field (HUDF) and Hubble Deep Field South as
where FWHMLSF and λ are both in Å.
Because of the atmospheric turbulence, we expect the PSF FWHM to be reduced with increasing wavelength. As was shown in Bacon et al. (2017), the change of the PSF with wavelength can be quite accurately modelled with a declining linear relation. To derive the slope and zero point of this relation in each MUSE field, we extracted as many stars as possible, only keeping those with a reliable MUSE redshift measurement of z ∼ 0. For each star, 100 sub-cubes of spatial dimension 10 × 10 pixels were extracted at regular intervals along the MUSE wavelength range and later collapsed into narrow band images using a fixed redshift slice depth of Δz = 0.01, scaling with wavelength as Δλ = Δz × λ. Each narrow band image was modelled with GALFIT (Peng et al. 2002a) using a symmetric
-
(i)
2D Gaussian profile,
-
(ii)
Moffat profile with a free β index.
We found consistent results between these two models, and therefore decided to use the Gaussian values in the following analysis. In order to remove small-scale variations while keeping the global declining trend of interest in the wavelength dependence of the PSF FWHM, we applied a rolling average with a window of five data points for all the stars. For each MUSE field, the median wavelength dependence of the PSF FWHM of the stars in the field was fitted with a linear relation. We find a median value of 0.65″ for the MUSE PSF FWHM and 2.55 Å for the LSF FWHM (roughly 50 km s−1). The values of the slope and zero point retrieved from the best-fit models were later used in the kinematics modelling (see Sect. 5).
2.2. HST data
In addition to using MUSE observations to extract the ionised gas kinematics, we also made use of Hubble Space Telescope Advanced Camera for Surveys (HST-ACS) images and photometry to model the morphology of the galaxies (see Sect. 4.1). For each galaxy we extracted stamps of dimension 4″ × 4″ in the F814W filter from the third public data release of the HST-ACS COSMOS observations (Koekemoer et al. 2007; Massey et al. 2010). These images have the best spatial resolution available (≲0.1″, that is, ∼600 pc at z ∼ 0.7) for HST data in the COSMOS field with a spatial sampling of 0.03″/pixel, as is required to extract precise morphological parameters, with an exposure time of 2028 s per HST tile. At the same time, this filter corresponds to the reddest band available (I-band) and therefore to the oldest stellar populations probed by HST data, being less affected by star-forming clumps and with smoother stellar distributions.
As for MUSE data, a precise knowledge of the HST PSF in this filter is required to extract reliable morphological parameters. To model the HST PSF FWHM, a circular Moffat profile was fitted onto 27 non saturated stars located in our MUSE fields. The theoretical values of the HST PSF parameters, retrieved from the best-fit Moffat profile, used in the morphological modelling (see Sect. 4.1) correspond to the median values of the 27 best-fit models parameters and are FWHMHST = 0.0852″ and β = 1.9, respectively (Abril-Melgarejo et al. 2021).
3. Galaxy sample properties
3.1. Initial MAGIC sample
Observations carried out for the MAGIC survey targeted already known galaxy groups in the COSMOS field such that all the galaxies in these fields up to z ∼ 1.5 were already detected from previous broadband photometry and listed in the COSMOS2015 catalogue of Laigle et al. (2016) up to a 3σ limiting magnitude of 27 in z++ band. The spectroscopic redshift of the objects in the COSMOS2015 catalogue located in the observed MUSE fields were estimated with the redshift finding algorithm Manual and Automatic Redshifting Software (MARZ; Hinton 2016) using both absorption and emission features. At the redshift of the targeted groups (z ∼ 0.7) the strongest emission lines are [O II]λλ3727, 3729, [O III]λ5007, and Hβ, and the main absorption lines are Ca II Hλ3968.47, Ca II Kλ3933.68, G band from CH molecules, and Balmer absorption lines. Following Inami et al. (2017), a PSF weighted spectrum was extracted for each source and a robust redshift determination was obtained using the strongest absorption and emission lines. In each case, a redshift confidence flag was assigned ranging from CONFID = 1 (tentative redshift) to CONFID = 3 (high confidence).
Initially, the catalogue contained 2730 objects, including stars in our Galaxy, intermediate, and high redshift (z ≥ 1.5) galaxies, 51% of which having reliable spectroscopic redshifts (CONFID > 1). As described in Sect. 5, the kinematics of the galaxies is extracted from the [O II] doublet. Therefore, as a starting point, we decided to restrict the sample of galaxies to [O II] emitters with reliable redshifts only, that is, galaxies in the redshift range 0.25 ≲ z ≲ 1.5 with CONFID > 1. The main reason for considering [O II] emitters only is that the bulk of galaxies located in the targeted groups is located at redshift z ∼ 0.7 where the [O II] doublet is redshifted into the MUSE wavelength range and happens to be among the brightest emission lines. Thus, using this emission line combines the advantages of having a high signal-to-noise ratio (S/N) extended ionised gas emission, while probing galaxies within a quite large redshift range roughly corresponding to 8 Gyr of galaxy evolution. Using the aforementioned criteria onto the initial MAGIC sample and without applying any further selection, the [O II] emitters sample contains 1142 galaxies. The main physical properties of this sample, along with other samples defined later in the text, are shown in Table 1.
3.2. Structure identification and characterisation
A crucial point when one wants to look at the effect of the environment on galaxy properties and evolution is to efficiently characterise the environment where galaxies lie. Galaxies are usually split into three main categories depending on their environment
-
(i)
field galaxies that do not belong to any structure,
-
(ii)
galaxies in groups that are gravitationally bound to a small number of other galaxies, and
-
(iii)
galaxies in clusters that are gravitationally bound to a large number of galaxies.
Because there is no sharp transition between a galaxy group and a galaxy cluster, and also because it is not particularly relevant for this discussion to disentangle between these two cases, we refer to both in the following parts as structures.
The characterisation of the galaxies’ environment and their potential membership to a structure was performed with a 3D friends-of-friends (FoF) algorithm. Structure membership assignment was performed galaxy per galaxy given that the sky projected and the line of sight velocity separations were both below two thresholds set to 450 kpc and 500 km s−1, respectively, as was suggested by Knobel et al. (2009). We checked that varying the thresholds around the aforementioned values by small amounts did not change significantly the structure memberships (see MAGIC survey paper, Epinat et al., in prep for more details). As shown in Fig. 1, the bulk of the structures is located in the redshift range 0.6 < z < 0.8 since most of them belong to the COSMOS wall (Scoville et al. 2007a; Iovino et al. 2016), a large-scale filamentary structure located at redshift z ≈ 0.72. Among these structures, those with at least ten members were studied in a previous paper (Abril-Melgarejo et al. 2021). In order to probe in detail the environmental dependence on galaxy properties, we use three sub-samples in the following sections:
 |
Fig. 1. Redshift distribution for the three initial sub-samples defined in Sect. 3.2. The samples of field galaxies (grey area) and galaxies in small structures (dashed blue line) have relatively flat distributions. The peak of the distribution for galaxies in large structures (red line) is located at redshift z ∼ 0.7 and is driven by the largest structures (40 ≲ N ≲ 100) found in the COSMOS area of the MAGIC sample. |
-
(i)
the field galaxy sub-sample, which contains galaxies not assigned to any structure as well as galaxies that belong to structures with up to three members,
-
(ii)
the small structure sub-sample, which comprises galaxies that belong to structures that have between three and ten members,
-
(iii)
the large structure sub-sample, which contains galaxies in structures with more than ten members.
Within the [O II] emitters sample, 45% belong to the field, 20% are in small structures, and 35% are in the large structure sub-sample.
3.3. Stellar mass and star formation rates
Since galaxies are located in the COSMOS area, we used the same 32 photometric bands as in Epinat et al. (2018) and Abril-Melgarejo et al. (2021) found in Laigle et al. (2016) (COSMOS2015) catalogue to derive additional physical parameters such as stellar masses and SFRs. We used the spectral energy distribution (SED) fitting code FAST (Kriek et al. 2009) with a synthetic library generated from the stellar population synthesis models of Conroy & Gunn (2010) using a Chabrier (2003) initial mass function, an exponentially declining SFR, a Calzetti et al. (2000) extinction law, and fixing the redshift of the galaxy to the spectroscopic redshift derived from the MUSE spectrum. The SED output parameters, including the stellar mass, SFR, and stellar metallicity, as well as their 1σ error, correspond to the values retrieved from the best-fit model of the SED, using the photometric bands values from Laigle et al. (2016) catalogue, and integrated within a circular aperture of diameter 3″.
After performing a careful comparison between the stellar masses and SFR values computed with FAST and those given in the COSMOS2015 catalogue (computed using LEPHARE SED fitting code), we found consistent results for the stellar masses with, on average, a scatter of 0.2 − 0.3 dex. On the other hand, we found larger discrepancies between the SFR values, around 0.7 − 0.8 dex. Given that the origin of this discrepancy is unclear, and that SED-based SFR estimates usually have quite large uncertainties (e.g., Wuyts et al. 2011; Leja et al. 2018), we decided to use emission lines instead to compute the SFR. Ultimately, one would want to use Hα as tracer of star formation, but given the MUSE wavelength range, this would restrict the sample to z ≲ 0.4 galaxies. Instead, following Kennicutt (1998b), we can use the [O II] doublet to compute the SFR in the entire [O II] emitters sample, as long as we can correct for Galactic and intrinsic extinctions, that is,
where SFR has not been normalised yet to account for the redshift evolution of the MS, ![$ L_\mathrm{{{[{\mathrm{O}\,\textsc{II}}]}}}\,=\,4 \pi D_L^2 F_\mathrm{{{[{\mathrm{O}\,\textsc{II}}]}, corr}} $](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq19.gif) is the [O II] luminosity, with DL the luminosity distance, and F[O II],corr the extinction corrected [O II] flux, which must be corrected for intrinsic extinction at the rest-frame Hα wavelength (Kennicutt 1992, 1998b), computed as
is the [O II] luminosity, with DL the luminosity distance, and F[O II],corr the extinction corrected [O II] flux, which must be corrected for intrinsic extinction at the rest-frame Hα wavelength (Kennicutt 1992, 1998b), computed as
with F[O II] the uncorrected [O II] flux integrated in an aperture of 3″, AHα the intrinsic extinction computed at the rest-frame Hα wavelength, and A[O II],MW the Galactic extinction computed at the observed [O II] wavelength assuming a Cardelli et al. (1989) extinction law and RV = 3.1. In order to compute the intrinsic extinction, one needs to know the extinction in a given band or at a given wavelength, for instance in the V band. This value is provided by FAST but, similarly to the SFR, it usually comes with large uncertainties. Given that the extinction plays an important role when deriving the SFR, we decided not to rely on the values from FAST. Instead, we used the prescription from Gilbank et al. (2010, 2011), which parametrises the extinction for Hα using the galaxies stellar mass as
for stellar masses M⋆ > 109 M⊙, and as a constant value below. When using the [O II]-based SFR in the analysis (Sect. 7), we checked that using the SED-based extinction rather than the prescription from Gilbank et al. (2010) to correct for intrinsic extinction did not change our conclusions.
The SFR-stellar mass plane for the kinematics sample (see Sect. 5.1), as well as the stellar mass and SFR distributions are shown in Fig. 2. In this figure and in what follows, we have taken out the zero point evolution of the MS by normalising the individual SFR values to redshift z0 = 0.7 using the prescription
 |
Fig. 2. SFR-M⋆ diagram for galaxies from the kinematics sample (see Sect. 6.1). Galaxies are separated between the field (black points), small structures (blue triangles), and large structures (red circles). The typical stellar mass and SFR error is shown on the bottom right. The SFR was normalised to redshift z0 = 0.7. The SFR and mass distributions are shown as histograms to the top and right, respectively, with the median values for each sample represented as lines of similar colours. |
where SFR and SFRz are the un-normalised and normalised SFR, respectively, and α is a scale factor. We used a value of α = 2.8 from Speagle et al. (2014), which is larger than the value of α = 1.74 derived and used in Boogaard et al. (2018) and Abril-Melgarejo et al. (2021). The main reason for normalising the redshift evolution with a larger slope is that the prescription from Boogaard et al. (2018) was derived on the low mass end (log10M⋆/M⊙ ⪅ 9) of the MS. However, most of our galaxies have stellar masses larger than this threshold where the redshift evolution of the MS is much steeper (e.g., Whitaker et al. 2014).
4. Galaxy morphology
4.1. Morphological modelling
To recover the galaxies morphological parameters, we performed a multi-component decomposition using the modelling tool GALFIT on HST-ACS images observed with the F814W filter. In order to have a fair comparison with previous findings from Abril-Melgarejo et al. (2021), we used the same methodology to model the morphology of galaxies. Therefore, we performed a multi-component decomposition with
-
(i)
a spherically symmetric de Vaucouleurs profile1 aimed at modelling the central parts of the galaxies (hereafter bulge) and
-
(ii)
a razor-thin exponential disk2 describing an extended disk (hereafter disk).
In most cases, we expect the disk component to dominate the overall flux budget, except within the central parts where the bulge is usually concentrated. In very rare cases where the galaxies do not show any bulge component, GALFIT always converged towards a disk component only model. On the opposite, in the case of elliptically shaped galaxies, GALFIT usually converges towards a single de Vaucouleurs component. We do not systematically try to model additional features that may appear in very few cases, such as clumps, central bars, or spiral arms. When clumps do appear, the multi-component decomposition is usually carried out without masking the clumps first. If the clumps seem to bias the morphological parameters of the main galaxy, a second run is done by either masking the clumps or adding other Sérsic profiles at their location. Unless there is no significant improvement in the robustness of the fitting process, the masked model is usually kept. Other cases may be galaxies in pairs or with small sky projected distances, which are modelled with an additional Sérsic profile at the second galaxy location, or out-of-stamps bright stars, which can contaminate the light distribution of some galaxies, in which case it is usually modelled with an additional sky gradient.
The aforementioned procedure was applied on the [O II] emitters sample. Among the 1142 galaxies, a few of them could not be reliably modelled with neither a bulge-disk decomposition nor a single disk or single bulge profile. Such galaxies turned out to be
-
(i)
low, or very low S/N objects for which the noise is contributing too much to the light distribution to extract reliable morphological parameters,
-
(ii)
very small galaxies for which the disk is barely resolved and the bulge not resolved at all.
After removing those cases, we get a morphological sample of 890 galaxies (i.e. 77% of the [O II] sample), which can be reliably modelled using this decomposition.
4.2. Morphological properties
The multi-component decomposition provides two scale parameters, the effective radius of the disk Reff,d, and that of the bulge Reff,b, but, in practice, we are more interested in the effective radius of the total distribution of light in the plane of the disk Reff. Even though there is no analytical formula linking Reff, Reff,d, and Reff,b, it can be shown from the definition of these three parameters that finding Reff amounts to solving the following equation (see Appendix C for the derivation):
where magd and magb stand for the disk and bulge apparent total magnitudes as provided by GALFIT, respectively, b1 ≈ 1.6783, b4 ≈ 7.6692, Γ is the complete gamma function, and γ the lower incomplete gamma function. Equation (6) is solved for each galaxy using a zero search algorithm considering the two following additional arguments
-
(i)
it always admits a single solution,
-
(ii)
Reff must be located between Reff,d and Reff,b.
To get an estimate of the error on the effective radius, we generate for each galaxy 1000 realisations by perturbing the bulge and disk magnitudes and effective radii using the errors returned by GALFIT and assuming Gaussian distributions. For each realisation, we solve Eq. (6) and then compute the error as the 1σ dispersion around the median value. The majority of the galaxies in the morphological sample are disk dominated, 80% of them having a bulge-to-total flux ratio B/T (Reff) < 0.5, with B/T as defined in Appendix C. As can be seen in Fig. 3, B/T distributions for galaxies from the morphological sample in the field, small, and large structure sub-samples are mostly similar, with very few bulge-dominated objects. There appears to be an excess of galaxies located in small structures with respect to field galaxies in the range 0.5 ≲ B/T ≲ 0.6 but, given the small number of galaxies in this bin (9), this excess may not be significant.
 |
Fig. 3. Bulge-to-total flux ratio distribution computed at one effective radius for galaxies in the morphological sample located in various environments. The legend is similar to that of Fig. 1. The vertical lines correspond to the median B/T values for each sample. The grey area in the background indicates which galaxies were selected in the kinematics sample (see Sect. 5.1). |
4.3. Stellar mass correction
As mentioned in Sect. 3.3, the galaxies stellar mass is retrieved from the SED fitting on the photometric bands in a circular aperture of 3″ on the plane of the sky. On the other hand, the gas rotation velocity V22 (see Sect. 7), is usually derived at R22 = 2.2 × Rd, where Rd = Reff,d/b1 is the disk scale length defined as the e-folding length with respect to the central value. This means that the SED-based stellar mass corresponds to the integrated mass within a cylinder of diameter 3″ orthogonal to the plane of the sky, whereas the kinematics is derived from the contribution of the mass located within a sphere of radius R22. Therefore, directly comparing the kinematics with the SED-based stellar mass in scaling relations such as the TFR adds additional uncertainties due to projection effects (inclination), different sizes (Reff,d, Reff,b), and different bulge and disk contributions (B/D). Thus, we decided to apply a correction to the SED-based stellar mass estimate in the following way, assuming a constant mass-to-light ratio across the galaxy,
where M⋆ and M⋆,corr are the uncorrected and corrected stellar masses measured in a 3″ circular aperture on the plane of the sky and in a sphere of radius R22 around the galaxy centre, respectively. In Eq. (7), Fsph corresponds to the integrated flux in a sphere of radius R22, while Fcirc corresponds to the integrated flux in a 3″ circular aperture on the plane of the sky.
In order to compute the mass correction, a high resolution 2D model was generated for each galaxy, projected on the sky given the axis ratio returned by GALFIT, and taking into account the impact of the MUSE PSF, whereas the flux in a sphere of radius R22 was integrated without taking into account the impact of the inclination, nor convoluting the surface brightness profile with the PSF. Taking into account the impact of the inclination and the PSF is important for the sky-projected model since the flux is integrated in a fixed aperture. Indeed, a higher inclination will result in the flux being integrated to larger distances along the minor axis, whereas higher PSF FWHM values will result in a loss of flux since it will be spread farther out. On the other hand, because the dynamical mass is derived in Sect. 5 from a forward model of the ionised gas kinematics taking into account the geometry of the galaxy and the impact of the PSF, the flux model integrated within a sphere of radius R22 must be fully free of projection and instrumental effects (i.e. inclination and PSF).
The impact of the stellar mass correction is shown in Fig. 4. For most galaxies the correction reduces the stellar mass, reaching at its maximum a factor of roughly 1.5. The main reason is that for R22 < 1.5″, the lower the disk effective radius, the more overestimated the SED-based stellar mass should be, though this argument must be mitigated by the fact that the inclination, the bulge contribution, and the PSF convolution can also play an important role in some cases, explaining why some galaxies have positive stellar mass corrections even with small disk effective radii.
 |
Fig. 4. Impact of stellar mass correction as a function of the SED-based stellar mass for galaxies from the morphological sample. Overall, the correction lowers the stellar mass, reducing it by as much as a factor of 1.5. We see that the smaller the disk radius, Reff,d (or equivalently R22), the larger the stellar mass reduction, consistent with the fact that the SED-based stellar mass computed in an aperture of 3″ usually overestimates the real value, though in practice this effect can be compensated for by sky projection and PSF effects. |
4.4. Stellar disk inclination and thickness
In Sect. 4.1 we assumed that the surface brightness of the stellar disk can be represented by a razor-thin exponential profile, but in practice we expect most disk components to have non-zero thickness. Not taking into account this finite thickness can bias morphological and kinematics measurements, especially in the central parts, and the circular velocity. In turn, this can bias the derived dynamical parameters such as the baryon fraction. This effect becomes even more relevant when considering that the stellar disks thickness is expected to evolve with redshift and mass. By modelling the q = b/a distribution, with a and b the apparent major and minor axes of the disk, respectively, for star-forming z ≤ 2.5 galaxies in the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey (CANDELS) field and from the Sloan Digital Sky Survey (SDSS) catalogue, van der Wel et al. (2014a) found that galaxy disks become thicker with increasing stellar mass and at larger redshift. Similarly, Zhang et al. (2019), by looking at the q − log a plane, reached a fairly similar conclusion. On top of that, galaxies that exhibit a combination of a thin blue disk and a thick red stellar disk are expected to have an observed thickness that varies with rest-frame wavelength. This effect can be observed in the catalogue of edge-on SDSS galaxies of Bizyaev et al. (2014), where the disk thickness of z ≲ 0.05 galaxies tends to almost systematically increase when measured in the g, r, and i bands, respectively. In order to get an estimate of the disk thickness in our sample of galaxies, we used the methodology described in Heidmann et al. (1972) and Bottinelli et al. (1983). If galaxies located at a given redshift z, with a fixed stellar mass M⋆, and emitting at a fixed rest-frame wavelength λ have a typical non-zero thickness q0(λ, z, M⋆), then the observed axis ratio q for the majority of the galaxies should reach a minimum value equal to q0 for edge-on galaxies. In our case, because the morphology is derived at a fixed observed wavelength λobs ≈ 814 Å (F814W HST filter), this condition can be written as
where λobs is the observed wavelength. The distribution of the observed axis ratio as a function of redshift is shown in Fig. 5. We see that the minimum observed axis ratio (i.e. highest −log10q) seems to decrease with redshift up to z ≈ 0.8 − 0.9 and remains roughly constant afterwards. This trend, which seems inconsistent with the fact that the disk thickness has been previously observed to increase with redshift, can be explained by the fact that higher redshift galaxies are seen at a bluer rest-frame wavelength, which probes younger stellar populations, and probably thinner disks. Due to the lack of edge-on galaxies in various mass bins, we do not observe a clear dependence of q on stellar mass, and therefore decided to model only the redshift dependence of q. In order to avoid placing too much weight on outliers that may have thinner disks than the typical thickness expected at a given redshift, we separated galaxies in eight redshift bins and computed the median thickness of the six most edge-on galaxies in each bin. The dependence of the stellar disk thickness with redshift is given by
 |
Fig. 5. Observed axis ratio, q, as a function of redshift for galaxies from the morphological sample (black points) after removing bulge-dominated galaxies and those with small disk sizes. The median values for the six most edge-on galaxies in redshift bins of width Δz = 0.15 are shown as red squares. The red line represents the thickness prescription that was applied. Independently of mass, galaxies tend to have thinner disks at larger redshifts, which may be due to the fact that we probe younger stellar populations at higher redshifts when observing in a single band. |
In the case of a razor-thin disk, the inclination i is related to the observed axis-ratio q through the relation cos i = q. However, for a disk with non-zero thickness, the relation between i and q will depend on the exact geometry of the disk. Assuming our disk galaxies can be well approximated by oblate spheroidal systems, we have (Bottinelli et al. 1983)
In Fig. 6, we show the distribution of the disk inclination for galaxies from the morphological sample (see Sect. 5.1) assuming razor-thin disks (black line), and after applying the thickness correction using Eqs. (9) and (10) (red hatched area). As expected, correcting for the disk thickness significantly increases the number of edge-on galaxies. Nevertheless, compared to the theoretical distribution (orange line), none of the distributions are consistent with randomly inclined galaxies. We find that we have an excess of galaxies in the range 60° ≲i ≲ 80°. The reason we are still missing some edge-on galaxies (i > 80°) might be that we did not try to model the impact of the dust, which is known to affect edge-on galaxies more severely. Nevertheless, the inclination distribution we get is quite similar to the distributions found in other studies where they also lack edge-on galaxies (Padilla et al. 2009; Foster et al. 2017).
 |
Fig. 6. Distribution of disk inclination for galaxies from the morphological sample, after removing bulge-dominated galaxies and those with small disk sizes. We show the distribution before correcting for the finite thickness of the disk (black line) and after the correction (red hatched area). The dashed orange line represents the binned theoretical distribution expected for randomly oriented disk galaxies. The correction tends to increase the fraction of edge-on galaxies. While being closer to the theoretical distribution at large inclinations, the corrected inclinations still do not match the distribution of randomly inclined galaxies. |
5. Galaxy kinematics
5.1. Kinematics modelling
Following the analysis in Abril-Melgarejo et al. (2021), we derived the ionised gas kinematics from the [O II] doublet only. For each galaxy, we extracted a sub-datacube with spatial dimensions 30 × 30 pixels around their centre and then performed a sub-resolution spatial smoothing using a 2D Gaussian kernel with a FWHM of 2 pixels in order to increase the S/N per pixel without worsening the datacube spatial resolution. From this smoothed version of the datacube, the [O II] doublet was fitted spaxel by spaxel by two Gaussian profiles with rest-frame wavelengths of 3727 Å and 3729 Å, respectively, assuming identical intrinsic velocity and velocity dispersion. Additionally, given the assumed photo-ionisation mechanisms producing the [O II] doublet (Osterbrock & Ferland 2006), we further constrained the flux ratio between the two lines as 0.35 ≤ F[O II]λ3727/F[O II]λ3729 ≤ 1.5. The aforementioned steps were performed with the emission line fitting python code CAMEL3, using a constant value to fit the continuum, and the MUSE variance cubes to weight the fit and estimate the noise. From this procedure, we recovered 2D maps for the following quantities: [O II] fluxes, S/N, velocity field, and velocity dispersion, as well as their corresponding spaxel per spaxel error estimation from the fit. To avoid fitting any noise or sky residuals that might appear in the flux and kinematics maps, especially in the outer parts of the galaxies, we cleaned the 2D maps in two successive steps: (i) through an automatic procedure, only keeping spaxels with S/N ≥ 5 and FWHM[O II] ≥ 0.8 × FWHMLSF(z), where FWHM[O II] and FWHMLSF are the [O II] spatial PSF and spectral LSF FWHM, respectively, and (ii) by visually inspecting the automatically cleaned velocity fields and manually removing remaining isolated spaxels or those with large velocity discontinuities with respect to their neighbours.
This led to the removal of 293 galaxies from the morphological sample (around 30%), mainly because they did not show any velocity field in their cleaned maps due to too low S/N per pixel. Because this cleaning process is mainly driven by S/N considerations, it is roughly similar to applying an [O II] integrated flux selection criterion of F[O II] ≳ 2 × 1018 erg s−1 cm−2.
The kinematics of the ionised gas in the remaining galaxies was modelled as a razor-thin rotating disk, using the method of line moments as described in Epinat et al. (2010). This method can quickly derive velocities maps by combining rotation curves4 from various components, taking into account the impact of spatial resolution on the derived velocity field, and the combined effect of the limited spatial and spectral resolutions on the velocity dispersion map. To derive the kinematics (circular velocity and velocity dispersion), we performed a mass modelling, taking into account prior knowledge from the morphological modelling. By using the best-fit GALFIT bulge and disk parameters from Sect. 4.1, and the disk thickness derived in Sect. 4.4, we fixed the rotation curves of the stellar disk and bulge components. Below we provide the main characteristics of the mass models used in the modelling, and we refer the reader to Appendix D for a detailed description of the models and rotation curves, as well as how implementing a finite thickness for the stellar disk impacts the estimate of the rotation of the gas. We assumed a double exponential density profile for the disk, which provides a surface brightness profile that is fairly similar to a single exponential distribution once projected onto the sky. In order to derive a density profile for the bulge component, one would need to numerically solve the inverse Abel transform for a de Vaucouleurs profile. But, because we required to have an analytical form for the bulge density, we decided to use instead a Hernquist profile (Hernquist 1990). As shown in Figs. D.4 and D.5, for the typical bulge parameters found in our sample, this functional form gives fairly reasonable surface brightness profiles once projected onto the sky. Finally, the DM halo was modelled using a Navarro-Frenk-White (NFW) profile (Navarro et al. 1996) with free parameters to account for constant or slowly declining observed rotation curves at large radii. This choice of DM parametrisation may not be entirely suitable with respect to observations that favour cored DM distributions. However, the core-cusp problem mainly affects the inner parts of the profiles. On the other hand, our goal is not to study the shape of DM haloes as a function of radius but rather to derive the ionised gas kinematics, the baryon, and the DM fractions where the inner shape of the DM halo has little impact on these quantities (Korsaga et al. 2019). In addition, because beam smearing strongly affects ground based observations of intermediate redshift galaxies, constraining robustly the inner DM halo distribution in detail remains a challenging problem but within reach (e.g., Genzel et al. 2020; Bouché et al. 2022). The effect of beam smearing can be seen in Fig. 7 where we compare the best-fit rotation curves between a mass model and a simpler flat model for galaxy 104-CGR79. Even though the intrinsic rotation curves in the inner parts differ (dashed orange line versus green full line), the deprojected (but beam-smeared) rotation curves are almost the same.
 |
Fig. 7. Rotation curves for the flat (green line) and mass models (orange dashed) of galaxy 104-CGR79 at redshift z = 0.53. The components are the bulge (red), the thin disk (blue), and the DM halo (black). We also show the observed de-projected (but beam-smeared) rotation curves extracted along the major axis from the observed velocity field map (black crosses), from the best-fit velocity field flat model (green circles), and from the best-fit velocity field mass model (orange triangles). The largest difference between the flat and mass models is found in the inner parts, where the beam smearing is the strongest. The total dynamical mass differs slightly between models, with the flat one being 4% higher than the mass model one. |
For each galaxy, a 2D velocity field model is generated and fitted onto the velocity field extracted from the cube. Since beam smearing artificially increases the value of the velocity dispersion recovered from the cube, especially near the central parts, modelling it and quadratically removing it from the velocity dispersion map allows us to extract a much more reliable estimator of the overall velocity dispersion in each galaxy. Given the above description, the kinematics model requires the following parameters:
-
(i)
centre coordinates,
-
(ii)
inclination,
-
(iii)
kinematics position angle (PA),
-
(iv)
systemic redshift zs,
-
(v)
disk rotation curve parameters VRT, max, Vcorr, max, Rd (see Appendix D.3),
-
(vi)
bulge rotation curve parameters Vb, max, a (see Appendix D.6),
-
(vii)
DM halo rotation curve parameters Vh, max and rs (see Appendix D.8),
-
(viii)
PSF size.
However, there exists a strong degeneracy between the kinematics centre and zs on one side, and the inclination of the disk and Vh, max on the other side, which is even stronger when the data are highly impacted by beam smearing. Therefore, to remove this degeneracy we fixed the kinematics centre and inclination assuming they are identical to their morphological counterparts. As previously stated, we also fix the parameters of the disk and bulge components since we assume they are entirely constrained from the morphology. Thus, the centre coordinates, the inclination, the disk and bulge rotation curve parameters (VRT, max, Vcorr, max, Rd, Vb, max and a) and the PSF model are fixed, whereas the kinematics PA, the systemic redshift, and the DM halo rotation curve parameters (Vh, max and rs) are free.
The kinematics modelling described above was performed with the new kinematics fitting code MOCKING5 using the python implementation of MULTINEST (Feroz & Hobson 2008); PyMULTINEST. MULTINEST is a Bayesian tool using a multi-nodal nested sampling algorithm to explore parameter space and extract inferences, as well as posterior distributions and parameter error estimation. To check our results, we ran MOCKING a second time but using this time the Levenberg-Marquardt algorithm, with the python implementation CAT_MPFIT6 of MPFIT (Markwardt 2009). Kinematics parameters were compared between these two methods as well as with earlier results obtained with an Interactive Data Language (IDL) code used in several previous studies (Epinat et al. 2009, 2010, 2012; Vergani et al. 2012; Contini et al. 2016; Abril-Melgarejo et al. 2021). A comparison of circular velocities obtained with MULTINEST and MPFIT can be found in Fig. A.1. We find consistent results between the methods, with MULTINEST providing more robust results. Thus, we use values from MULTINEST in the following parts. In addition, we performed a similar kinematics modelling but using an ad hoc flat model for the rotation curve as described in Abril-Melgarejo et al. (2021), in order to check the mass modelling and assess its reliability. After checking the morphological, kinematics, and mass models on the remaining galaxies, we decided to remove four additional objects:
-
(i)
106-CGR84, 21-CGR114, and 101-CGR79 because they show signs of mergers in their morphology and kinematics, which may bias the measure of their dynamics, as well as their stellar mass estimate and thus their mass modelling,
-
(ii)
13-CGR87 because it lies on the edge of the MUSE field with only half of its [O II] flux map visible.
Once these objects are removed, we get a kinematics sample of 593 galaxies with morphological and kinematics mass and flat models.
An example of a mass model with its corresponding flat model is shown in Fig. 7 for a disk-like galaxy with a non-zero (but weak) bulge contribution. The mass model rotation curve (orange dashed line) for the galaxy, which appears to be DM dominated, is consistent with the simpler flat model (green line), especially at R22 where the rotation velocity is inferred. Examples of full morpho-kinematics models for four types of galaxies are shown in Fig. 8 with, in the top-left corner, a galaxy with a close companion in its HST image and with a velocity field similar to that of a large fraction of galaxies in our sample, in the top-right corner an edge-on galaxy, in the bottom-left corner a large disk-dominated galaxy with visible arms and clumps, and in the bottom-right corner a small galaxy with a prominent bulge and a highly disturbed velocity field. These four examples give a decent overview of the types of galaxies, morphologies and kinematics we have to deal with in the MAGIC survey.
 |
Fig. 8. Examples of morpho-kinematics modelling for galaxies with IDs 132-CGR32 and 104-CGR79 (both in large structures) and 77-CGR30 and 86-CGR114 (both in the field). In each panel, from top to bottom and left to right: (a) HST-ACS image, (b) GALFIT model, (c) HST residuals, (d) CAMEL velocity field, (e) MOCKING velocity field model, (f) velocity field residuals, (g) CAMEL velocity dispersion map, (h) MOCKING beam smearing model, including spectral resolution broadening, and (i) beam smearing and LSF corrected velocity dispersion map. The morpho-kinematics centre and the morphological PA are respectively shown in the HST image and the CAMEL maps as a green cross and a green line, whose length corresponds to R22. The PSF FWHM is indicated as the grey disk in the velocity field. The [O II] surface brightness distribution is overlaid on top of the HST and MUSE [O II] flux maps, with contours at levels Σ[O II] = 2.5,5,10,20,40, and 80 × 10−18 erg s−1 cm−2 arcsec−2. |
6. Sample selection
6.1. Selection criteria
Before analysing morpho-kinematics scaling relations as a function of environment, and following the discussion in Abril-Melgarejo et al. (2021; Sect. 3.6), we must first apply a few selection criteria to the kinematics sample depending on the scaling relation studied. The three relations analysed in this paper are the size-mass relation, MS relation, and TFR. Among the three, the TFR is the one that requires the most stringent criteria since we must ensure that we have good constraints on both the stellar mass and the kinematics measurements, which translates as having reliable constraints on the disk parameters (size, inclination), on the [O II] S/N, and on the dynamical modelling. On the other hand, we only require disk-dominated MS galaxies to analyse the size-mass and MS relations. Thus, we define a common sample for both the size-mass and MS relations, named the MS sample, by applying the following selection criterion:
-
(i)
B/D (Reff)≤1,
where B/D (Reff) is the bulge-to-disk flux ratio computed at one effective radius. This criterion ensures that we only have disk-dominated galaxies in the sample. In Abril-Melgarejo et al. (2021), we used a second selection criterion to remove red sequence galaxies located below the MS since we were only interested in star-forming galaxies. For the kinematics sample, applying this criterion would only remove two additional galaxies, since most of the red sequence galaxies also tend to be bulge dominated. Thus, we decided not to apply this criterion in the next parts. When applying the B/D selection, we end up with a MS sample of 447 galaxies.
Concerning the TFR, we must ensure that we have good constraints on the disk size, inclination, and [O II] S/N, as well as on the dynamical modelling, since they can all have significant impact on the kinematics and the derived dynamical masses. To ensure the TFR is not impacted by poor constraints on any of these parameters, we applied the following additional criteria on top of the B/D selection:
-
(ii)
Reff,d ≥ 0.5 × FWHM(z),
-
(iii)
![$ (\mathrm{S/N})_\mathrm{{tot}} \geq 40 \times \sqrt{\pi \left [R_{\mathrm{eff}, \rm{d}}^2 + \left ({\mathrm{FWHM}}(z) / 2 \right )^2 \right ]} $](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq28.gif) ,
, -
(iv)
25° ≤i ≤ 75°,
-
(v)
f⋆ ≤ 1 − Δf⋆,
where Reff,d is the disk effective radius and FWHM(z) the MUSE PSF FWHM computed at the [O II] doublet wavelength at the redshift of the galaxy (see Sect. 2.1), both in arcsec. In criterion (iv), i is the inclination after correcting for the finite thickness of the stellar disk, and in (v), f⋆ = M⋆,corr/(M⋆,corr + MDM) is the stellar fraction, with M⋆,corr and MDM the stellar and DM halo mass, respectively, both computed at R22. The uncertainty on the stellar fraction Δf⋆ is computed by propagating measurement and fit errors on both the stellar mass and the circular velocity. In (iii), the total S/N is computed as
where F[O II](x,y) and S/N(x, y) correspond to the [O II] flux and S/N cleaned maps, respectively (see Abril-Melgarejo et al. 2021). Criterion (ii) is used to remove unresolved galaxies, that is, galaxies for which the stellar disk is smaller than the PSF, and criterion (iii) takes into account the dependence of the S/N on the effective radius, and is derived by assuming a constant surface brightness map, as well as a constant S/N map with a S/N per pixel of at least eight across one observed effective radius ( ). As a consistency check, we also looked at how using a different threshold (S/N)tot ≥ 30 would impact the selection. This threshold adds 40 new galaxies, but the majority are either small with respect to their MUSE PSF FWHM or do not show clear velocity gradients. Thus, we decided to use criterion (ii) in the next parts. We show in Fig. 9, the galaxies distribution and selection in terms of S/N, Reff,d/FWHM, and B/D for galaxies from the kinematics sample. Criterion (iv) removes face-on and edge-on galaxies because, for the former, uncertainties are too large to reliably constrain the rotation of the ionised gas and, for the latter, the mass models used in the kinematics modelling are much more loosely constrained.
). As a consistency check, we also looked at how using a different threshold (S/N)tot ≥ 30 would impact the selection. This threshold adds 40 new galaxies, but the majority are either small with respect to their MUSE PSF FWHM or do not show clear velocity gradients. Thus, we decided to use criterion (ii) in the next parts. We show in Fig. 9, the galaxies distribution and selection in terms of S/N, Reff,d/FWHM, and B/D for galaxies from the kinematics sample. Criterion (iv) removes face-on and edge-on galaxies because, for the former, uncertainties are too large to reliably constrain the rotation of the ionised gas and, for the latter, the mass models used in the kinematics modelling are much more loosely constrained.
 |
Fig. 9. S/N-disk effective radius-B/D selection plot for galaxies from the kinematics sample. The disk size selection criterion is represented as the vertical line. The S/N selection criterion depends on the FWHM, which varies with redshift and MUSE field. As an example, we show the S/N limit used for a typical FWHM of 0.65″. Points are colour-coded according to their bulge-to-disk ratio computed at one effective radius. The grey areas give an idea of the galaxies eliminated by the size and S/N selection criteria. We also show the ten galaxies eliminated by selection criterion v (orange crosses) and the three we decided to keep (orange circles). |
Finally, criterion (v) identifies galaxies whose dynamical modelling failed, that is, for which we overestimated the contribution of baryons to the total rotation curve. This corresponds to 13 galaxies in the kinematics sample. Among them, we decided to remove ten galaxies, namely 85-CGR35, 28-CGR26, 257-CGR84, 113-CGR23, 83-CGR23, 38-CGR172, 130-CGR35, 110-CGR30, 105-CGR114, and 100-CGR172. These objects are shown as orange crosses in Fig. 9. Most of them tend to be quite small or with low S/N values even though they pass criteria (i) and (ii), but also have velocity fields with a quite low amplitude (∼30 − 40 km s−1). This means that any uncertainty on their morphological modelling and mass-to-light ratio will have a stronger impact on their dynamical modelling. In addition, galaxies 85-CGR35 and 28-CGR26 have disturbed morphologies and/or kinematics, which may be due to past merger events or to a more complex morphology than the bulge-disk decomposition performed in Sect. 4.1. On the contrary, after carefully investigating their morphology and kinematics, we decided to keep galaxies 378-CGR32, 20-CGR84, and 19-CGR84 since they seemed to be intrinsically ‘baryon dominated’. After applying criteria (i) to (v), we end up with a TFR sample of 146 galaxies.
In Sect. 7 we may apply two additional selection criteria when it is necessary to have comparable parameter distributions between different environments:
-
(vi)
log10M⋆ [M⊙] ≤ 10,
-
(vii)
0.5 < z < 0.9.
Criterion (vi) is used to have comparable samples in terms of stellar mass (see stellar mass distributions in Fig. B.4), whereas (vii) only keeps galaxies in a 1 Gyr interval around redshift z ≈ 0.7 where most of the galaxies in the large structures are located. Thus, this criterion allows us to check that our results may not be impacted by a potential redshift evolution.
6.2. Summary of the different samples and sub-samples
To clarify the difference between the various samples used in this paper, we provide below a summary of their characteristics. We also show in Table 1 the distribution of their main physical parameters represented by their median value, 16th and 84th percentiles.
-
(1)
[O II] emitters sample: 1142 [O II] emitters with reliable spectroscopic redshift in the range 0.25 ≲ z ≲ 1.5.
-
(2)
Morphological sample: 890 galaxies from the [O II] emitters sample with reliable bulge-disk decomposition.
-
(3)
Kinematics sample: 593 galaxies from the morphological sample with reliable kinematics.
-
(4)
MS sample: 447 disk-dominated galaxies from the kinematics sample selected in B/D only. This sample is used to study the size-mass and MS relations.
-
(5)
TFR sample: 146 disk-dominated galaxies from the MS sample with selection criteria from (i) to (v) applied to only keep galaxies with well constrained kinematics. This sample is used to study the TFR.
We show in Table 2 the median properties for each environment-based sub-sample of galaxies from the MS sample later used in the analysis. Among these, we show the field, small, and large structure ones defined in Sect. 3.2. Alternatively, when analysing the TFR in Sect. 7.4, we also split the entire sample into two sub-samples only: a field and small structure sub-sample on the one hand, and a large structure sub-sample on the other hand. This separation is performed because using the previously defined sub-samples would lead to too few galaxies in the small structures to reliably constrain their TFR. In the following and in Table 2, we refer to these sub-samples as Small-N and Large-N, where N corresponds to the richness threshold used to classify galaxies in either the field and small structure or large structure sub-samples. We note that the terms ‘small’ and ‘large’ used to name the sub-samples never refer to the size nor the mass of the structures, only to the number of galaxy members.
Median properties for various sub-samples of galaxies from the MS sample.
The main properties shown in Table 2 are the total number and the proportion of galaxies in each sub-sample, the stellar, gas, and dynamical masses computed within R22 = 2.2Rd, with Rd the disk scale length, the extinction corrected [O II]-based SFR, and the median disk effective radius Reff, d. All the sub-samples have mostly similar gas mass and SFR distributions. However, the sub-samples that target the largest structures tend to have on average larger disk sizes and stellar masses. Their dynamical masses are slightly larger as well, though the difference between small and large structures at a fixed threshold is roughly 0.3–0.4 dex, similar to the difference seen in stellar masses, indicative that these massive structures do not host, on average, more massive DM haloes. Interestingly, when using the largest threshold values N = 15, 20, the large structure sub-samples have larger stellar masses (Δlog10M⋆ ≈ 0.5 dex), but similar dynamical masses with respect to the small structure sub-samples. One of the key difference visible in Fig. 2 is the stellar mass distribution. The large structure sub-sample is more extended than the field and the small structure sub-samples towards larger stellar masses, so that almost all the galaxies beyond M⋆ > 1010 M⊙ are located in the large structures. These massive galaxies also tend to have the largest SFR values, though their impact on the SFR distribution is not as clearly visible as in the stellar mass distribution.
The MAGIC catalogue containing the main morpho-kinematics and physical properties for galaxies from the MS sample is available at the Centre de Données astronomiques de Strasbourg (CDS). We provide in Table F.1 a description of the columns appearing in the catalogue. Appendix G contains the morpho-kinematics maps as shown in Fig. 8 for all galaxies in the TFR sample.
7. Analysis
We focus the analysis on the size-mass relation, the MS relation, and the TFR. We consider the MS and TFR samples and separate galaxies into three different sub-samples, targeting different environments. For the size-mass relation, we use the corrected stellar mass M⋆,corr, which better traces the disk and bulge masses within a sphere of radius R22 (see Sect. 4.3), and the disk scale length Rd = Reff,d/b1 for the size of our galaxies, where Reff,d is the disk effective radius and b1 ≈ 1.6783. We also use M⋆,corr for the TFR, as well as the total circular velocity V22 derived at R22 from the best-fit mass and flat models for the velocity. This R22 value corresponds to where the peak of rotation for the disk component is reached and is typically used in similar studies (Pelliccia et al. 2019; Abril-Melgarejo et al. 2021). Lastly, for the MS, we use the SED-based stellar mass M⋆ derived in an aperture of 3″ and the extinction corrected and normalised [O II] SFR as described in Sect. 3.3. Each scaling relation is fitted with the form
where y is the dependent variable, x is the independent variable, and p is a pivot point equal to the median value of log10x when using the full samples (MS or TFR). For each relation, we decided to always use stellar mass as the independent variable, so that the pivot point is p = 9.2. As pointed out in Williams et al. (2010), Pelliccia et al. (2017), this is justified for the TFR as fitting the opposite relation yields a slope biased towards lower values, while for the size-mass and MS relations we find more robust fits and smaller dispersion.
In order to have fits not biased by points with underestimated errors in x and y, we quadratically added an uncertainty on the error of both independent and dependent variables in each scaling relation. Based on Abril-Melgarejo et al. (2021), we decided to quadratically add an uncertainty of 0.2 dex on the stellar mass and the SFR, and of 20 km s−1 on the velocity, consistent with typical uncertainties and systematics found in the literature. For the size estimate, we added a slightly lower uncertainty of 0.065 dex, which corresponds to a relative error of roughly 15%, slightly below the more or less 30% scatter Kuchner et al. (2017) found when comparing size measurements between Subaru and HST data.
We used two different tools to perform the fits. The first one is LTSFIT (Cappellari et al. 2013), a python implementation of the Least Trimmed Square regression technique from Rousseeuw & Van Driessen (2006), and the second one is MPFITEXY (Williams et al. 2010) IDL wrapper of MPFIT. Both methods take into account uncertainties on x and y, as well as the intrinsic scatter of each relation, but LTSFIT implements a robust method to identify and remove outliers from the fit. However, it currently does not have an option to fix the slope. Therefore, whenever we needed to fix the slope, we used MPFITEXY, removing beforehand outliers found by LTSFIT.
7.1. Impact of selection
We start by looking at how the aforementioned scaling relations are impacted by the different selection criteria used to select the MS and TFR samples. To do so, we fitted each scaling relation using the MS sample with LTSFIT, letting the slope free, and we looked at the impact of the size (ii) and/or S/N (iii) criteria on the best-fit results. Additionally, since we also apply the inclination (iv) and the mass modelling uncertainty (v) selections on the TFR, we also consider their impact on the slope and zero point of this relation. The results for each scaling relation are shown in Table 3. We also show in Fig. 10 the population of galaxies removed by each selection criterion, as well as the galaxies removed when applying a redshift cut 0.5 < z < 0.9 (red upper triangles), and the remaining galaxies (black points). We find that the size-mass relation is mainly impacted by the size selection for both the slope and zero point, while the S/N criterion has a weaker effect. When removing small galaxies, the slope is biased towards lower values, and this effect is more important for field galaxies than for galaxies in other sub-samples. Similarly, the MS is mainly affected by the size selection while the S/N selection has almost no impact. This result may seem surprising given that, as can be seen in Fig. 10, size-removed (blue downward pointing triangles), and S/N-removed (oranges squares) galaxies tend to lie along the MS, but on opposite parts. However, the size selection has a stronger impact since it mainly removes low mass galaxies, biasing the slope to larger values driven by more massive galaxies.
 |
Fig. 10. Impact of the different selection criteria from Sect. 6.1 applied to the size-mass relation (top left), the TFR (bottom left), and the MS relation (bottom right). Black circles represent galaxies that remain when all the selection criteria are applied. Given that some selections remove similar galaxies, we show those removed by the S/N (orange squares), size (blue downward-pointing triangles), and redshift criteria (red triangles), in this order. Additionally, we also show the galaxies removed by the inclination selection (green diamonds) in the TFR before the redshift selection was applied. |
Comparison of fit parameters for the scaling relations with various selection criteria.
Finally, similarly to the size-mass and MS relations, the TFR is also mainly impacted by the size selection. Removing small galaxies changes the slope to lower values, driven by more massive galaxies. However, when applying the size and S/N selections, both the slope and zero point values become close to the original ones. Because of the mass models used, the TFR is quite tight and those criteria tend to remove almost symmetrically galaxies with low and high circular velocity as can be seen in Fig. 10, so that the remaining galaxies fall along the original TFR without any bias. Important selection criteria for the TFR are the inclination and mass modelling uncertainty (iv and v). Among the two, criterion (v) has the weakest impact since it only removes a handful of galaxies, whereas the inclination selection (iv) tends to remove a significant fraction of galaxies with larger circular velocities than the bulk of galaxies with stellar masses beyond 109 M⊙. These galaxies probably have overestimated circular velocities, so that including them in the fit of the TFR would lead to a slope biased towards larger values.
Because the size and S/N selection criteria were defined to select galaxies with reliable morphology and kinematics for the mass modelling, and because they can bias the slope and zero point of the size-mass and MS relations, we decided not to apply them to select the MS sample, as described in Sect. 6.1. However, these criteria, in combination with the inclination (iv) and mass modelling uncertainty (v) selections, are important to have an unbiased fit of the TFR. Thus, we decided to apply selection criteria from (i) to (v) to select the TFR sample in Sect. 6.1.
7.2. Impact of the environment on the size-mass relation
We fitted the sub-samples that target different environments by fixing the best-fit slope to the value from LTSFIT when considering the entire MS sample with the same selection criteria. We further applied two additional selection criteria, a mass cut M⋆ < 1010 M⊙ and a redshift cut 0.5 < z < 0.9, in order to reduce the impact of different mass and redshift distributions between sub-samples on the best-fit zero points. We show in Table 4 the best-fit zero points as well as the slopes used for each fit and in Fig. 11 the size-mass relation and its best-fit line when applying the mass (vi) and redshift cuts (vii). We also provide in Fig. B.1 the size-mass relation and its best-fit line when only applying the mass cut, and when applying neither mass nor redshift cuts.
 |
Fig. 11. Size-mass relation for galaxies from the MS sample with additional mass and redshift cuts applied (vi and vii). Symbols and colours are similar to those in Fig. 2, and orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit lines are shown when using a richness threshold N = 10 (full lines) and N = 20 (dashed lines). The dashed black line is not visible since field galaxies have the same best-fit line for N = 10 and N = 20. We do not show galaxies in the small structure sub-sample since too few galaxies remain after selection criteria (vi) and (vii) are applied. We also provide in the top left the slope and best-fit zero point for each sub-sample (see Eq. (12) with y = Rd and x = M⋆). The typical uncertainty on stellar mass and disk size is shown in the bottom right as a grey error bar. After controlling for differences in mass and redshift, we find a 1σ significant difference of 0.03 dex between sub-samples with N = 10, and a 2σ significant difference of 0.06 dex with N = 20. |
Best-fit values for the size-mass and MS relations fitted on the MS sample.
We find a small offset in the zero point between sub-samples. When applying both mass and redshift cuts, the difference amounts to 0.03 dex, which is at most 1σ significant7. Similarly, when applying only the mass cut, we get a 1σ significant difference between the field sub-sample and the small and large structure sub-samples. However, if we apply neither cuts, we get a slightly larger offset of 0.04 dex between the field and the large structure one, and almost similar zero points between the field and the small structure one. In Fig. 11 and in Table 4, we used the disk size to fit the size-mass relation, whereas other studies (e.g., Maltby et al. 2010) usually use a global radius. To check whether the choice of radius might have an impact on our results we fitted the size-mass relation, but using the global effective radius derived in Sect. 4.2. Even when using the global radius, we get the same trend as before, with an offset of 0.02 dex (1σ significant). If we use instead a more stringent richness threshold of N = 20 to separate galaxies between small and large structures, we do find a larger offset of 0.06 dex (2σ significant) between the field and the large structure sub-samples when using the disk radius as a size proxy, and a similar offset of 0.02 dex when using the global effective radius.
Overall, if significant, the difference between the field and the largest structures when using N = 10 is quite small. We note that this result is different from what was found in previous studies such as Maltby et al. (2010) or Matharu et al. (2019). Indeed, such studies always found a weak but significant dependence of the size-mass relation with environment. For instance, Maltby et al. (2010) found spiral galaxies in the field to be about 15% larger than their cluster counterparts but, in our case, it would only amount to a size difference of roughly 7%. Instead, using the offset value with N = 20, we get a size difference of roughly 14%, consistent with previous findings from Maltby et al. (2010) that galaxies in the most massive structures are more compact than those in the field. Given the models used in the morphological analysis and because the bulge-to-disk ratio is fairly similar between sub-samples, the zero point of the size-mass relation directly translates in terms of the galaxies central surface mass density of the disk component (i.e. extrapolated from the Sérsic profile at R = 0). Assuming the flux of the disk component dominates at R22, using a slope α = 0.34 and a zero point βsm, we get the following scaling relation for the disk component central surface mass density ΣM, d(0) as a function of stellar mass:
where βsm = 0.26 ± 0.03 for the field sub-sample and βsm = 0.20 ± 0.03 for the large structure sub-sample when using a richness threshold of N = 20. A change in the zero point of the size mass relation does not impact the slope of Eq. (13) but only its zero point. Thus, the 0.06 dex offset measured between the field and the most massive structures results in a negative offset of −1.2 dex in Eq. (13). We note that this interpretation remains true as long as we can neglect the flux of the bulge at R22. However, when we can no longer neglect it, then Eq. (13) will have an additional non-linear term that is a function of the bulge central surface mass density and effective radius. In this case, the interpretation would be more complex as galaxies could have different bulge or disk physical properties as a function of environment but still align on the same size-mass relation. However, as is visible in Fig. C.1, the bulge contribution at R22 is on average and independently of environment around 10% of the total flux, which amounts to a scatter in the size-mass relation of about 0.1 dex, which is sufficiently small to neglect at first order the bulge contribution in this relation.
7.3. Impact of the environment on the MS relation
To study the MS, we use the SED-based stellar mass and the [O II] SFR corrected for extinction and normalised to redshift z0 = 0.7 as described in Sect. 3.3. For this relation, applying both a mass and a redshift cut is important. Indeed, as can be seen in Fig. A.3, the MS can be quite sensitive to redshift since there is still a small dichotomy between low and high redshift galaxies even after normalisation. The main reason for this effect is that the MAGIC survey is designed to blindly detect sources in a cone. The blind detection makes the survey flux-limited, which means we are missing faint, low SFR galaxies in the highest redshift bin. Besides, we expect to see an excess of massive galaxies in the most massive structures with respect to the field, which, in our sample, are all located at redshift z ≈ 0.7. Thus, the survey design tends to create a dichotomy in mass, which is visible in SFR as well since we are focussing on star-forming galaxies. Nevertheless, as can be seen in Table 4, the redshift cut has a much smaller effect than the mass cut, especially on the slope value from the best-fit line.
We show in Fig. 12 the MS with both cuts applied for the field and large structure sub-samples, as well as their best-fit lines and zero point values. We also provide in Fig. B.2 the MS and its best-fit line when only applying the mass cut, and when applying neither mass nor redshift cuts. Independently of whether we apply a mass and/or redshift cut or not, we find a more than 2σ significant difference in the zero point (∼0.1 dex) between the field and large structure sub-samples. However, there is almost no difference in the zero point between the field and the small structure sub-samples. Independently of the cut applied, the field galaxies always have a larger zero point than the galaxies in the large structures. If we interpret this difference in terms of a SFR offset between the field and the largest structures, this would lead to an average SFR for the galaxies in the large structures that is about 1.3 times lower than that in the field. This factor is quite close to the recent value found by Old et al. (2020a,b) using the GOGREEN and GCLASS surveys at redshift z ∼ 1. On the other hand, the reason why other studies such as Nantais et al. (2020) do not find any impact of the environment on the MS is still unclear. The effect of the redshift evolution of the MS might play a role, since Nantais et al. (2020) probe clusters at z ∼ 1.6, which is beyond the 0.5 < z < 0.9 redshift range we restricted our fit to. Similarly, the impact of the environment on the MS may be segregated between low and high mass galaxies. As was reported in Old et al. (2020a,b), the MS seems to be more impacted in the lowest mass regime. This explanation would be compatible with our result where we mainly probe low to intermediate mass galaxies since we remove massive galaxies not to bias the fit.
 |
Fig. 12. SFR-stellar mass relation for galaxies from the MS sample with additional mass and redshift cuts applied (vi and vii). Symbols and colours are similar to those in Fig. 2, and orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit lines are shown when using a richness threshold N = 10 (full lines) and N = 20 (dashed lines). We do not show galaxies in the small structure sub-sample since too few galaxies remain after selection criteria (vi) and (vii) are applied. The SFR is normalised to redshift z0 = 0.7 (see Sect. 3.3). We also provide the slope and best-fit zero point for each sub-sample in the top left (see Eq. (12) with y = SFR and x = M⋆). The typical uncertainty on stellar mass and SFR is shown in the bottom right as a grey error bar. Even after controlling for differences in mass and redshift, we find a 2σ significant difference of 0.10 dex between sub-samples with N = 10, and a 3σ significant difference of 0.15 dex with N = 20. |
Similarly to Sect. 7.2, we performed the same fits but using a more stringent richness threshold of N = 20 to separate between structures. When using this threshold combined with both mass and redshift cuts, we find a roughly 3σ significant difference of 0.15 dex (βMS = − 0.22 ± 0.04 for field galaxies, βMS = − 0.37 ± 0.05 for galaxies in the largest structures), consistent with our previous finding that galaxies in the largest structures have reduced SFR with respect to the field. With this offset, we get an average SFR in the most massive structures that is about 1.5 times lower than that in the field, still quite close to the value from Old et al. (2020a,b).
7.4. Impact of the environment on the TFR
We look at the TFR as a function of the environment using the TFR sample. Since too few galaxies remain in the small structure sub-sample once all the selection criteria (i to v) are applied, we decided to focus this analysis on two sub-samples only. We fit the TFR using different richness thresholds (N = 5, 10, 15 and 20) to separate galaxies into a field and small structure and a large structure sub-samples. The best-fit zero points and the slopes values are shown in Table 5 and in Fig. 13. As a comparison, we also show on the bottom panel of Fig. 13 the TFR obtained using a simpler flat model for the rotation curve as defined in Abril-Melgarejo et al. (2021). This model allows us to measure the galaxies circular velocity without any prior on the baryon distribution and is therefore not affected by our mass modelling.
 |
Fig. 13. Stellar mass TFR at R22 for galaxies from the TFR sample with mass and redshift cuts applied (vi and vii). The top panel shows the TFR using the velocity computed from the mass models, and the bottom shows the TFR using the velocity from a flat model. Galaxies are split between field and small structure (black points) and large structure (red circles) sub-samples using a richness threshold of N = 10. Orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit linear relations for both sub-samples are shown as full lines. We provide in the bottom part of each panel the slope and best-fit zero points (see Eq. (12) with y = V22 and x = M⋆,corr). The typical uncertainty on stellar mass and velocity is shown as a grey error bar. After controlling for differences in mass and redshift, we do not find any impact of the environment on the zero point of either TFR. |
Best-fit values for the TFR fitted on the TFR sample.
We find a similar trend between the TFR from the mass models and that from the flat model. Overall, the tightness of the relation using either model makes the zero point values well constrained, with typical uncertainties around 0.03 dex. When we do not apply any mass or redshift cut, the large structure sub-sample tends to systematically have a lower zero point between 0.02 dex and 0.04 dex with respect to the field sub-sample depending on the richness threshold used8. This is shown in Table 5, as well as in Fig. B.3. However, when adding a mass and/or a redshift cut, this offset tends to disappear independently of the model and richness threshold used, as is shown in Fig. 13. When using N = 20, we nevertheless get a small 1σ significant offset of roughly 0.04 dex in both TFR. This result suggests that the larger offset values found when applying no cut are certainly the consequence of having different stellar mass distributions between the two sub-samples, or might be due to a small impact of the redshift evolution of the TFR.
Given the disk, bulge and DM halo mass models used to derive the circular velocity (see Sects. 5 and D), and assuming a constant B/D value of 3%, which is the median value found in the kinematics sample independently of environment, we can write the TFR as a function of the stellar mass M⋆,corr within R22, the stellar fraction f⋆(R22) = M⋆,corr/[M⋆,corr + MDM(R22)], with MDM the DM halo mass, both computed at R22, and Rd as
In Eq. (14), we see the size-mass relation. Thus, rewriting Eq. (14) to make the central surface mass density of the disk component appear, and then inserting Eq. (13), we get
where βsm is the size-mass relation zero point that was found to vary with environment in Sect. 7.2. In Eq. (15), we see that only two terms can contribute to an offset on the TFR:
-
(i)
different zero points on the size-mass relation as a function of environment,
-
(ii)
an offset on the stellar fraction measured within R22 between the field and the large structure sub-samples.
If we interpret any offset on the TFR zero point as being an offset on stellar mass at fixed circular velocity, given Eq. (15) we have
where Δβsm is the offset on the zero point of the size-mass relation that is due to the contraction of baryons observed in the most massive structures. With a threshold N = 20, we have Δβsm = 0.06 dex and an offset on the TFR, which is in circular velocity at fixed stellar mass, of 0.04 dex and 0.05 dex for the mass and flat models, respectively. The corresponding offset in stellar mass at fixed circular velocity is given by −ΔβTFR/αTFR = 0.11 dex for both models. For a typical galaxy in the kinematics sample with a stellar fraction of 20% this would give a difference between a galaxy in the field and one in the largest structures of roughly 4%. This result is quite close to the difference in stellar fraction (circles) seen in Fig. 14 where we have plotted its evolution computed from the mass models in bins of stellar mass between galaxies in the field and small structures (black) and those in large structures (red). We see that the stellar fraction increases as we go towards more massive galaxies, both in the field and in large structures. However, the difference remains small compared to the uncertainty of roughly 10%. Besides, the distributions tend to be quite spread out, as is shown by the grey error bars, even though there is a significant offset of the stellar fraction distribution and of its dispersion as we go towards larger stellar masses.
 |
Fig. 14. Evolution of the median stellar and baryon fractions for galaxies from the TFR sample in the field (black points) and in large structures (red circles) as a function of stellar mass in mass bins of 1 dex. Light grey error bars correspond to the 16th and 84th percentiles of the baryon fraction distributions. The typical uncertainty on stellar mass and baryon fraction is shown as a dark grey error bar on the bottom right. Because we removed galaxies whose mass models have large uncertainties (selection criteria iv and v), the fractions we measure are probably slightly underestimated. |
Contrary to what was found in Abril-Melgarejo et al. (2021), we cannot measure an impact of quenching on the TFR since our stellar mass offset is negative, meaning that galaxies in the largest structures would be on average more massive than those in the field. Nevertheless, the difference is quite small (∼0.05 dex) and may not be particularly significant. However, we do measure a significant offset in the MS, which means that quenching does take place somehow within at least some of the galaxies in the largest structures. One way to explain the apparent discrepancy is to look at the timescale over which the SFR we used in the MS is probed. Indeed, we measure the SFR from the [O II] doublet, which mainly probes recent star formation (∼10 Myr). On the other hand, if we consider that the field and large structure sub-samples do not have zero points more different than at most their uncertainty (0.02 − 0.03 dex), we can compute an upper bound on the quenching timescale in the large structures using Eq. (16) of Abril-Melgarejo et al. (2021). This gives us timescales between roughly 700 Myr and 1.5 Gyr, significantly larger than the ∼10 Myr probed by the SFR from the [O II] doublet. Hence, the galaxies in the largest structures at z ∼ 0.7 might have quite recently started being affected by their environment, and thus started being quenched, so that the impact on the TFR might not be visible yet with respect to the field galaxies.
Some authors also implement an asymmetric drift correction to take into account the impact of gas pressure on its dynamics (e.g., Meurer et al. 1996; Úbler et al. 2017; Abril-Melgarejo et al. 2021; Bouché et al. 2022). Evaluated at R22, the gas pressured corrected circular velocity for a double exponential density profile with a constant thickness writes (Meurer et al. 1996; Bouché et al. 2022)
where V22 is the uncorrected circular velocity evaluated at R22 and σV is the velocity dispersion computed as the median value of the beam smearing and LSF corrected velocity dispersion map. Equation (17) is only an approximation of the real impact of gas pressure on the measured circular velocity since it only holds for turbulent gas disks with negligible thermal pressure. In the kinematics sample, the median value of the intrinsic velocity dispersion is around 30 km s−1 independently of environment. Thus, the impact of the asymmetric drift correction is quite small on the TFR. However, we find that the velocity dispersion is not constant but is correlated with stellar mass such that more massive galaxies are more impacted by the correction than low mass ones. In turn, this tends to align high and low mass galaxies onto a line with roughly the same slope, but with a slightly larger scatter. Indeed, when implementing the asymmetric drift correction, we find virtually the same zero point between the small and large structure sub-samples (βTFR ≈ 2.07 with the corrected velocity versus βTFR ≈ 2.02 with the uncorrected one), independently of the environment or the richness threshold used.
Additionally, we can also include the gas mass into the fit. We compute the gas mass using the Schmidt-Kennicutt relation (Schmidt 1959; Kennicutt 1998a) assuming the gas is evenly distributed within a disk of radius R22:
with Mg the gas mass and SFR the un-normalised SFR (see Sect. 3.3). If we replace the size and SFR variables in Eq. (18) by the size-mass and SFR-mass relations found before, we get a correlation between gas and stellar masses such that more massive galaxies also have a higher gas mass. In particular, the offset on the zero point found for the TFR between the field and the large structure sub-samples will also lead to a small offset in the gas mass-stellar mass relation. The impact of the gas mass on the mass budget is shown in Fig. 14. We compare the stellar fraction (circles) with the total baryon fraction (triangles) for the field and large structure sub-samples. For most galaxies, the gas mass is non-negligible but has a small impact, leading to an offset between stellar and baryon fractions of roughly 5%. On the other hand, the gas mass has a slightly more significant impact on the lowest mass bin. While the impact is similar to other mass bins for the field sample (roughly 5%), the impact on the large structure sub-sample is stronger, reaching about 10%. This would suggest that the low mass galaxies are more gas rich in the large structures than in the field. However, only a handful of galaxies (∼10) are located in the lowest mass bin in the large structure sub-sample. Besides, as is shown by the light grey error bars in Fig. 14, the distribution for the baryon fraction is quite large so that the difference in gas mass is probably not that significant. Another explanation for this slightly larger difference found at low mass might be that these galaxies are experiencing bursts of star formation, which would lead to overestimated gas masses, but this effect is not visible in the MS.
When the gas mass is included, we get a tighter TFR, with low mass galaxies that tend to be aligned onto the same line as the high mass ones. In turn, this brings the best-fit slope to a value of α = 0.31 when applying the mass and redshift cuts, quite close to the α = 0.29 value found when fitting the stellar mass TFR without applying any cut (i.e. driven by massive galaxies). The zero point is almost always similar between the field and small structure and large structure sub-samples (βTFR ≈ 1.99), independently of the richness threshold used to separate galaxies in the two sub-samples. Similarly to the stellar mass TFR, only when using a threshold N = 20 do we find a slightly more significant difference in zero point between the field and small structure sub-sample (βTFR = 2.00 ± 0.02) and the large structure sub-sample (βTFR = 1.98 ± 0.02). However, once we further include the asymmetric drift correction from Eq. (17), the difference vanishes for any richness threshold used (βTFR ≈ 2.02).
Thus, if there is an impact on the TFR, it is mostly driven by differences in terms of stellar mass or redshift distributions rather than the environment itself. We note that this result is consistent with Pelliccia et al. (2019), where they could not find an impact of the environment on the TFR as well, but is contradictory to what was found in Abril-Melgarejo et al. (2021). By comparing their sample to others, such as KMOS3D, KROSS, and ORELSE, they were able to find a significant offset in the TFR, which they attributed to the fact that different environments were probed. This offset was interpreted either as the effect of quenching, which reduces the amount of stellar mass in the most massive structures at fixed circular velocity, or as the effect of baryon contraction, which leads to an increase in circular velocity at fixed stellar mass. As discussed previously, baryon contraction and quenching are visible in our size-mass and MS relations, but not in the TFR. However, they noted that performing a consistent and reliable comparison between samples using different observing methods, models, tools, and selection functions was a difficult task and can lead to multiple sources of uncertainty. These can directly arise from the morphological and kinematics modelling, but can also be driven by uncertainties on the SED-based stellar masses, which, depending on the SED fitting code used and the assumptions made on the star formation history, can lead to systematics of the same order of magnitude as the offset found in Abril-Melgarejo et al. (2021). On the other hand, we argue that our result is quite robust since we have applied the same models, tools, assumptions and selection from the beginning to the end.
8. Conclusion
We have performed a morpho-kinematics modelling of 1142 [O II] emitters from the MAGIC survey using combined HST and MUSE data in the redshift range 0.25 < z < 1.5. These galaxies are all located in the COSMOS field and have been attributed to structures of various richness (field, small, and large structures) using a FoF algorithm. We derived their global properties, such as their stellar mass, using the SED fitting code FAST and their SFR using the [O II] doublet. Their morphological modelling was performed with GALFIT on HST F814W images using a bulge and a disk decomposition. The best-fit models were later used to perform a mass modelling to constrain the impact of the baryons on the total rotation curve of the ionised gas. We included a mean prescription for the thickness of stellar disks as a function of redshift to correct for the impact of finite thickness on the mass and rotation curve of the disk component. The kinematics maps (line flux, velocity field, velocity dispersion, etc.) were extracted from the MUSE cubes using the [O II] doublet as kinematics tracer, and the 2D kinematics modelling was performed by fitting the baryon mass models combined with an NFW profile to describe the DM halo directly on the observed velocity field while modelling the impact of the beam smearing to compute the intrinsic velocity dispersion.
Our kinematics sample was divided into sub-samples, targeting different environments, and we decided to focus our analysis on three scaling relations, namely the size-mass relation, the MS relation, and the TFR. As a first step, we selected a sample of star-forming disk-like galaxies and studied how using different additional selection criteria, in terms of size, S/N, and/or redshift, would impact the best-fit slope and zero point for each relation. We found that the redshift and mass selection criteria were important in order not to bias the zero point when comparing between environments since their redshift and mass distributions differ. Additionally, the TFR requires additional criteria, especially in terms of inclination, to remove galaxies with poorly constrained kinematics.
We find a 1σ significant difference (0.03 dex) in the size-mass relation as a function of environment when using a richness threshold of N = 10 to separate between small and large structures, and a 2σ significant difference (0.06 dex) using N = 20. This result suggests that galaxies in the largest structures have, on average, smaller disks (∼14%) than their field counterparts at z ≈ 0.7, similar to what was found in the literature. Additionally, we get similar results when using the global effective radius rather than the disk effective radius for our disk sizes. Regarding the MS, we find a 2σ significant impact of the environment on the zero point of the MS (0.1 dex) when using N = 10 and a 3σ significant difference (0.15 dex) when using N = 20. These offsets are consistent with galaxies located in the large structures with SFRs reduced by a factor of 1.3 − 1.5 with respect to field galaxies at a similar redshift.
Finally, after applying mass and redshift cuts, we cannot find any difference in the zero point of the TFR between environments, except when using a richness threshold of N = 20 to separate between a structure sub-sample and a large structure sub-sample. In this instance, we get an offset of 0.04 dex, which is significant to at most 1σ significance. By interpreting this offset as being an offset in stellar mass at fixed circular velocity, and by including the contribution of the size-mass relation in the interpretation of the TFR, we find that there must be a small difference of roughly 4% in stellar fraction between field galaxies and those in the largest structures. Because we measure a negative stellar mass offset in the TFR between the field and the large structure sub-samples (galaxies in the large structures are more massive than those in the field), we can rule out the effect of quenching, as was suggested in Abril-Melgarejo et al. (2021), when using N = 20. On the other hand, because there is no measured difference in zero point with N = 5, 10, and 15, we can compute upper bounds on the quenching timescale of the galaxies in the large structures using the typical uncertainty found on the TFR zero point. If quenching does indeed lead to a deficit in stellar mass in structures at z ≈ 0.7 with respect to the field, this would suggest that galaxies have been impacted by the largest structures for at most between 700 Myr and 1.5 Gyr. When including the contribution of the gas in the mass budget of the TFR, we find a similarly significant offset of 0.02 dex between the field and the large structures (using N = 20). However, as previously discussed, quenching is still ruled out since this leads to a negative mass offset. Nevertheless, we note that these small differences in zero point vanish once we include the contribution of gas pressure in the dynamics (asymmetric drift correction).
The conclusion from our fully self-consistent study differs from that of Abril-Melgarejo et al. (2021), even though they investigated and took methodological biases between the samples they compared into account as much as possible. Such a difference might be due to uncontrolled biases when they compared the TFR between samples, or from a possible redshift evolution of the TFR since they could not control the redshift distribution of the various samples as much as we did in this analysis.
This outlines the importance of further reducing those biases by using similar datasets, selection functions, and analysis methods for galaxies in both low- and high-density environments to measure the impact of the environment on galaxy evolution.
Supplementary Material
Full Appendix G Access here
For a derivation of this approximation, see Eq. 8.73 in Chapter 8 of Bovy J. Dynamics and Astrophysics of Galaxies. Princeton University Press, Princeton, NJ (in preparation) whose online version can be found at https://galaxiesbook.org/.
Acknowledgments
We dedicate this article in memory of Hayley Finley. This work was supported by the Programme National Cosmology et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES. This work has been carried out through the support of the ANR FOGHAR (ANR-13-BS05-0010-02), the OCEVU Labex (ANR-11-LABX-0060), and the A*MIDEX project (ANR-11-IDEX-0001-02), which are funded by the “Investissements d’avenir” French government program managed by the ANR. This work has been carried out thanks to the support of the Ministry of Science, Technology and Innovation of Colombia (MINCIENCIAS) PhD fellowship program No. 756-2016. JCBP acknowledges financial support of Vicerrectoría de Investigación y Extensión de la Universidad Industrial de Santander under project 2494. This research has made use of MATPLOTLIB (Hunter 2007), SCIPY (Virtanen et al. 2020), NUMPY (Harris et al. 2020) and ASTROPY (Astropy Collaboration 2013, 2018). We acknowledge David Carton for his investment in the build-up of the project.
References
- Abril-Melgarejo, V., Epinat, B., Mercier, W., et al. 2021, A&A, 647, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balogh, M. L., van der Burg, R. F. J., Muzzin, A., et al. 2020, MNRAS, 500, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Bizyaev, D. V., Kautsch, S. J., Mosenkov, A. V., et al. 2014, ApJ, 787, 24 [Google Scholar]
- Boogaard, L. A., Brinchmann, J., Bouché, N., et al. 2018, A&A, 619, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Epinat, B., Contini, T., et al. 2019, A&A, 631, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottinelli, L., Gouguenheim, L., Paturel, G., & de Vaucouleurs, G. 1983, A&A, 118, 4 [NASA ADS] [Google Scholar]
- Bouché, N., Murphy, M. T., Kacprzak, G. G., et al. 2013, Science, 341, 50 [Google Scholar]
- Bouché, N. F., Bera, S., Krajnovic, D., et al. 2022, A&A, 658, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Conroy, C., & Gunn, J. E. 2010, ApJ, 712, 833 [Google Scholar]
- Contini, T., Epinat, B., Bouché, N., et al. 2016, A&A, 591, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Catinella, B., & Smith, R. 2021, PASA, 38, e035 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & Songaila, A. 1977, Nature, 266, 501 [Google Scholar]
- Davé, R. 2009, in Galaxy Evolution: Emerging Insights and Future Challenges, eds. S. Jogee, I. Marinova, L. Hao, & G. A. Blanc, ASP Conf. Ser., 419, 347 [NASA ADS] [Google Scholar]
- Dimauro, P., Huertas-Company, M., Daddi, E., et al. 2018, MNRAS, 478, 5410 [Google Scholar]
- Duncan, K., Conselice, C. J., Mundy, C., et al. 2019, ApJ, 876, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Contini, T., Le Fèvre, O., et al. 2009, A&A, 504, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epinat, B., Amram, P., Balkowski, C., & Marcelin, M. 2010, MNRAS, 401, 2113 [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epinat, B., Contini, T., Finley, H., et al. 2018, A&A, 609, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Erfanianfar, G., Popesso, P., Finoguenov, A., et al. 2016, MNRAS, 455, 2839 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foster, C., van de Sande, J., D’Eugenio, F., et al. 2017, MNRAS, 472, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [Google Scholar]
- Freundlich, J., Combes, F., Tacconi, L. J., et al. 2019, A&A, 622, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Price, S. H., Übler, H., et al. 2020, ApJ, 902, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbank, D. G., Baldry, I. K., Balogh, M. L., Glazebrook, K., & Bower, R. G. 2010, MNRAS, 405, 2594 [NASA ADS] [Google Scholar]
- Gilbank, D. G., Baldry, I. K., Balogh, M. L., Glazebrook, K., & Bower, R. G. 2011, MNRAS, 412, 2111 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Driver, S. P., Petrosian, V., et al. 2005, AJ, 130, 1535 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. E., Wolf, C., Barden, M., et al. 2009, MNRAS, 393, 1275 [Google Scholar]
- Guérou, A., Krajnović, D., Epinat, B., et al. 2017, A&A, 608, A5 [Google Scholar]
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Heidmann, J., Heidmann, N., & de Vaucouleurs, G. 1972, MmRAS, 75, 85 [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [Google Scholar]
- Hinton, S. 2016, MARZ: Redshifting Program, Astrophysics Source Code Library [record ascl:1605.001] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2012, MNRAS, 421, 3522 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [Google Scholar]
- Inami, H., Bacon, R., Brinchmann, J., et al. 2017, A&A, 608, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., Petropoulou, V., Scodeggio, M., et al. 2016, A&A, 592, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, W. 1983, MNRAS, 202, 995 [NASA ADS] [Google Scholar]
- Kelkar, K., Aragón-Salamanca, A., Gray, M. E., et al. 2015, MNRAS, 450, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1992, ApJ, 388, 310 [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998a, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., Jr 1998b, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2012, ApJ, 753, 121 [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [Google Scholar]
- Korsaga, M., Epinat, B., Amram, P., et al. 2019, MNRAS, 490, 2977 [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [Google Scholar]
- Kuchner, U., Ziegler, B., Verdugo, M., Bamford, S., & Häußler, B. 2017, A&A, 604, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., & Dokkum, P. V. 2018, ApJ, 854, 62 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [Google Scholar]
- Lubin, L. M., Gal, R. R., Lemaux, B. C., Kocevski, D. D., & Squires, G. K. 2009, ApJ, 137, 4867 [CrossRef] [Google Scholar]
- Maltby, D. T., Aragón-Salamanca, A., Gray, M. E., et al. 2010, MNRAS, 402, 282 [Google Scholar]
- Mantha, K. B., McIntosh, D. H., Brennan, R., et al. 2018, MNRAS, 475, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Massey, R., Stoughton, C., Leauthaud, A., et al. 2010, MNRAS, 401, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Matharu, J., Muzzin, A., Brammer, G. B., et al. 2019, MNRAS, 484, 595 [Google Scholar]
- Meurer, G. R., Carignan, C., Beaulieu, S. F., & Freeman, K. C. 1996, ApJ, 111, 1551 [CrossRef] [Google Scholar]
- Mowla, L. A., van Dokkum, P., Brammer, G. B., et al. 2019, ApJ, 880, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2009, ApJ, 698, 1934 [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nantais, J., Wilson, G., Muzzin, A., et al. 2020, MNRAS, 499, 3061 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1995, MNRAS, 275, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., & Teyssier, R. 2008, MNRAS, 390, 1326 [Google Scholar]
- Old, L. J., Balogh, M. L., van der Burg, R. F. J., et al. 2020a, MNRAS, 500, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Old, L. J., Balogh, M. L., van der Burg, R. F. J., et al. 2020b, MNRAS, 493, 5987 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito, CA: University Science Books) [Google Scholar]
- Padilla, N. D., Lagos, C., & Strauss, M. 2009, in The Monster’s Fiery Breath: Feedback in Galaxies, Groups, and Clusters, eds. S. Heinz, & E. Wilcots, Am. Inst. Phys. Conf. Ser., 1201, 100 [Google Scholar]
- Pelliccia, D., Tresse, L., Epinat, B., et al. 2017, A&A, 599, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelliccia, D., Lemaux, B. C., Tomczak, A. R., et al. 2019, MNRAS, 482, 3514 [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002a, AJ, 124, 266 [Google Scholar]
- Peng, Q.-H., Peng, F., Chou, C.-K., & Lin, Y.-H. 2002b, Ap&SS, 282, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y. J., Lilly, S. J., Kova, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
- Rousseeuw, P. J., & Van Driessen, K. 2006, Data Min. Knowl. Discovery, 12, 29 [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schroetter, I., Bouché, N. F., Zabl, J., et al. 2019, MNRAS, 490, 4368 [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007a, ApJS, 172, 1 [Google Scholar]
- Scoville, N., Aussel, H., Benson, A., et al. 2007b, ApJS, 172, 150 [Google Scholar]
- Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Tacconi, L. J., Genzel, R., Saintonge, A., et al. 2018, ApJS, 853, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Tiley, A. L., Bureau, M., Cortese, L., et al. 2019, MNRAS, 482, 2166 [Google Scholar]
- Toomre, A. 1963, ApJ, 138, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Úbler, H., Förster Schreiber, N. M., Genzel, R., et al. 2017, ApJ, 842, 121 [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014a, ApJ, 788, 28 [Google Scholar]
- van der Wel, A., Chang, Y.-Y., Bell, E. F., et al. 2014b, ApJ, 792, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Ventou, E., Contini, T., Bouché, N., et al. 2017, A&A, 608, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventou, E., Contini, T., Bouché, N., et al. 2019, A&A, 631, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergani, D., Epinat, B., Contini, T., et al. 2012, A&A, 546, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Walter, F., Carilli, C., Neeleman, M., et al. 2020, ApJ, 902, 111 [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, M. J., Bureau, M., & Cappellari, M. 2010, MNRAS, 409, 1330 [Google Scholar]
- Wuyts, S., Färster Schreiber, N. M., Lutz, D., et al. 2011, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zabl, J., Bouché, N. F., Schroetter, I., et al. 2019, MNRAS, 485, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Primack, J. R., Faber, S. M., et al. 2019, MNRAS, 484, 5170 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional plots and tables
 |
Fig. A.1. Comparison of the circular velocity V22 = V(R22) using MOCKING between MULTINEST and MPFIT for galaxies from the MS sample. The rotation curve used was a flat model, and we removed galaxies whose circular velocity could not be reliably constrained (R22 falls outside the range where there is sufficient S/N in the MUSE data cube to derive the kinematics). Red points correspond to galaxies visually classified as having no apparent velocity field in their kinematics maps, and dashed red lines correspond to a 50% difference between the two methods. The typical uncertainty is shown in the bottom-right part of the plot. Overall, values are consistent within their error bars. |
 |
Fig. A.2. Distribution of effective radii for galaxies in the morphological sample. In grey (filled) we show the total size, in red (hatched) the bulge size, and in blue (hatched) the disk size. Disks are mostly found between roughly 1 kpc and 6 kpc, with very few galaxies with disk sizes beyond 10 kpc. The lack of disks below 1 kpc is due to the size selection criterion from Sect. 6.1. On the other hand, the majority of bulges are found below 2 kpc. The total size of galaxies is mainly driven by the disk component. |
 |
Fig. A.3. SFR-stellar mass relation for galaxies from the MS sample, colour-coded as a function of redshift. Despite the applied normalisation to redshift z0 = 0.7, we still see a dichotomy. High redshift galaxies tend to align along lines with the largest specific star formation rate (sSFR), while low redshift galaxies tend to align along lines with the lowest sSFR because of the survey design. |
Appendix B: Impact of selection
 |
Fig. B.1. Size-mass relation with and without applying the mass selection criterion (vi) on galaxies from the MS sample. The data points and best-fit lines are similar to Fig. 11. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the right panel. The typical uncertainty on stellar mass and disk size is shown on both panels as a grey error bar. |
 |
Fig. B.2. SFR-mass relation with and without applying the mass selection criterion (vi) on galaxies from the kinematics sample. The data points and best-fit lines are similar to Fig. 12. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the right panel. The typical uncertainty on stellar mass and SFR is shown on both panels as a grey error bar. |
 |
Fig. B.3. TFR with and without applying the mass selection criterion (vi) on galaxies from the TFR sample. The data points and best-fit lines are similar to Fig. 13. The first row shows the TFR using the velocity derived from the best-fit mass models, and the second row the TFR using the flat model. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the rightmost panels. The typical uncertainty on stellar mass and velocity is shown on each panel as a grey error bar. |
 |
Fig. B.4. Impact of selection criteria on the main parameters distributions for galaxies from the kinematics sample. Each row represents a different selection. The black full line corresponds to the field galaxy sub-sample, the blue dashed line to the small structures and the red thick line to the large structures (using a threshold of N = 10 to separate between structures). We also show the median values for each sub-sample as vertical lines. We do not show the small structure sub-sample in the last two rows since there remain too few galaxies. |
Appendix C: Bulge-disk decomposition
Figure C.1 represents the median value of the bulge-to-total flux ratio (B/T) for the morphological sample as a function of radius. We see that beyond one effective radius the disk dominates the flux budget. When computed near the centre, B/T is close to one, consistent with the bulge dominating the inner parts. Even though the disk dominates at large distances, B/T does not reach zero. This is a consequence of the chosen bulge-disk decomposition. Indeed, for a Sérsic profile with parameters (n, Σeff, Reff), the integrated flux up to radius r is given by
 |
Fig. C.1. Mean B/T for galaxies in the morphological sample computed at various radii in units of Reff. The areas correspond to the 1σ (dark grey) and 2σ (light grey) dispersions. The bulge component dominates the central parts of the galaxies whereas the disk takes over completely after roughly one effective radius. Even as far as 10Reff, we find a nearly constant non-zero B/T ≈ 0.2 indicative of a non-negligible bulge contribution to the overall flux budget. |
where γ is the lower incomplete gamma function and where bn is the solution of the equation Γ(2n) = 2γ(2n,bn) (Graham et al. 2005), with Γ the complete gamma function. Therefore, for a bulge-disk decomposition the total flux ratio between the two components is given by
where (Σeff,b,Reff,b) and (Σeff,d,Reff,d) are the bulge and disk parameters, respectively. The only case for which Eq. C.2 vanishes is when the bulge contribution can be neglected with respect to the disk. Otherwise, when B/T(∞) is sufficiently larger than 0, this reflects a non-negligible contribution of the bulge to the overall flux budget. The fact that the median value for the morphological sample is around 0.2 is therefore a good indication of the relevance of performing a bulge-disk decomposition with respect to using a single disk model.
The half-light radius of a multi-component decomposition involving only Sérsic models does not necessarily have to be computed through numerical integration but can also be derived by finding the single zero of a given function. Indeed, for a bulge-disk decomposition, from the definition of the global half-light radius (that is, the radius that encloses half of the total flux), we have
where Fd(Reff) and Fb(Reff) are the disk and bulge fluxes at the global effective radius Reff, and Ftot, d, Ftot, b are the disk and bulge total fluxes, respectively. Given Eq. C.1, one can rewrite Eq. C.3 as
Furthermore, if one defines the total magnitude of a component i as magi = − 2.5 log 10Ftot,i + zpt, where zpt is a zero point that is the same for all the components and normalises by the total flux, then Eq. C.4 simplifies to
with the function f defined as
Equation C.5 can be solved by searching for a zero in the range [min(Reff,d,Reff,b), maxReff,d,Reff,b)]. Indeed, if Reff > max(Reff,d,Reff,b), the flux at Reff would be the sum of Fd(Reff) > Fd, tot/2 and Fb(Reff) > Fb, tot/2 such that it would be larger than the expected Ftot/2 value. Thus, Reff cannot be greater than max(Reff,d,Reff,b), and the same argument can be given for the case Reff < min(Reff,d,Reff,b).
Finally, there is only one zero that is a solution of Eq. C.5, and this can be shown by noticing that f is a monotonously increasing function of x whose normalised form f(x)/f(∞) is bounded between -1 for x = 0 and 1 for x = ∞.
Appendix D: Mass modelling
The methodology used in Abril-Melgarejo et al. (2021) to derive the galaxies dynamics is only an approximation of the intrinsic ionised gas kinematics. The flat model used for the rotation curve is ad hoc, based on observations of local and intermediate redshift rotation curves of DM-dominated galaxies. While being a good approximation for DM-dominated systems, this kinematics modelling does not take into account information from the morphological modelling. In theory, one should derive the ionised gas kinematics, assuming in our case that the gas is distributed within an infinitely thin disk, from the 3D mass distribution of the different galaxy components. Even though we do not have access to such distributions, we can nevertheless constrain the gas kinematics under a few assumptions. In Sect. 4.1 we assumed that the sky projected surface density of the stars can be described by a bulge-disk decomposition, where the surface density of stellar disk is represented by an exponential profile and the stellar bulge is assumed to be spherically symmetric with a surface density described by a de Vaucouleurs profile. If one can find 3D flux densities that, when projected onto the line of sight, become the corresponding surface densities, then one has found the corresponding mass densities up to a multiplicative factor that is the mass-to-light ratio Υ = (M/L)⋆.
D.1. Theoretical background
For any mass density ρM(r), we can derive the corresponding potential Φ from Poisson equation
The observed velocity maps are derived from the ionised gas kinematics, which is assumed to be located within an infinitely thin disk; therefore, we are only interested in the velocity of the gas within the plane of the galaxy disk. If we further assume that the mass distribution ρM is in equilibrium within its gravitational potential, then the centrifugal acceleration caused by its rotation must balance the radial gradient of the potential Φ in the galaxy plane, that is,
with Vcirc the circular velocity, R the radial distance in the plane of the galaxy, and where we have assumed that the potential and circular velocity are independent of the azimuth because of the symmetry of the mass distributions used in the following. Since the mass distributions and therefore the potentials add up, the circular velocity can be simply written as
where Vcirc, i is the circular velocity of the component i obeying Eq. D.2 for the corresponding potential well. In our case, the components that will contribute the most to the rotation curve are the stellar disk, stellar bulge and the DM halo to account for constant or slowly declining observed rotation curves at large radii. We do not model the contribution of the gas, which will therefore slightly contribute to the DM halo profile. In the case of the stellar components, we transform from stellar light distributions ρi to mass distributions ρM, i using
where we have further assumed that the mass-to-light ratio, Υ, is constant throughout the galaxy, and we compute it using the SED-based estimator of the stellar mass as
where M⋆ is the SED-based mass computed in a circular aperture of diameter 3″, and FSP(1.5″) is the flux integrated on the plane of the sky in the same aperture. In this analysis, we assume a similar Υ for both disk and bulge because it would require at least two HST bands to constrain efficiently the M/L for both components individually as done for instance in Dimauro et al. (2018).
D.2. Razor-thin stellar disk
To begin with, we assume the stellar disk to be infinitely thin, so that the stellar light density can be written as
where ΣRT represents the light distribution in the plane of the disk, with ΣRT(0) the central surface density, b1 ≈ 1.6783, Reff,d the disk effective radius, and δ is the Dirac distribution. The rotation curve for such a distribution was computed for the first time by Freeman (1970) using the method described in Toomre (1963):
with  and y = R/(2Rd). The effective radius of the disk is related to the disk scale length appearing in Eq. D.8 through Reff,d = b1Rd. The maximum circular velocity is reached at a radius R = 2.15Rd and is equal to
and y = R/(2Rd). The effective radius of the disk is related to the disk scale length appearing in Eq. D.8 through Reff,d = b1Rd. The maximum circular velocity is reached at a radius R = 2.15Rd and is equal to
where G is the gravitational constant.
D.3. Thin stellar disk
To refine the mass modelling of the stellar disk, we consider a disk model with a finite thickness. Assuming the light distribution can be correctly represented by a double exponential profile, we have
where hz is the disk scale height. It can be shown (Peng et al. 2002b) that the potential in the plane of the galaxy for such a density can be written as
where S0(k) is the Hankel transform of order 0 of the surface density Σd(R). For thin disks with small hz, an approximation of the circular velocity in the plane of the galaxy is given by9
where VRT is the razor-thin circular velocity defined in Eq. D.8 and Rd is the disk scale length. For typical values of hz/Rd ≈ 0.2 − 0.3, this approximation gives a circular velocity that is different from numerical integration by less than 2% for most of the radial range, except near the central parts where the relative difference rises, though the absolute difference remains negligible in practice as the circular velocity quickly drops to zero near the centre. The maximum of the correction is reached at Rd (see Fig. D.1) and is given by
 |
Fig. D.1. Impact of the thickness on the shape of the rotation curve for a thin disk. The finite thickness only impacts the inner parts and changes both the amplitude and the radius where the maximum is reached. |
D.4. Impact of thickness on inclination and central surface density
In the case of a razor-thin disk projected at an inclination i with respect to the line of sight, the apparent central surface density ΣRT, obs(0) and axis ratio q = b/a, with a and b the semi-major and semi-minor axes, respectively, scale with the inclination as
Writing Eq. D.14 is equivalent to saying that the total flux of the disk must be independent of its inclination on the sky, and Eq. D.15 comes from the fact that the isophotes of a projected razor-thin disk are ellipses. However, in the case of a disk with non-zero thickness the surface density profile gets more complicated, and must be computed as the integral of the inclined density distribution along the line of sight. We give in Appendix E a derivation of this integral in the general case. For the apparent central density, it simplifies to
with q0 = hz/Rd the real axis ratio, Rd the disk scale length, ΣRT(0) the central surface density if the galaxy was seen face-on, and i0 the real inclination of the galaxy. We see that when the disk is infinitely thin (i.e. hz = 0) we recover Eq. D.14, as should be expected. For a perfectly edge-on galaxy, that is, i = 90°, Eq. D.14 diverges, which is due to the fact that a razor-thin disk seen edge-on does not have its flux distributed onto a surface anymore, but onto a line. For a disk with non-zero thickness, this is not the case, and therefore Eq. D.16 remains finite for an edge-on galaxy.
For a disk with finite thickness, there is no trivial way to relate the observed axis ratio q to the real one q0. In practice, the isophotes of a projected disk can be approximated by ellipses but with an ellipticity that depends on position, disk scale length, scale height, and inclination. Still, we expect the observed axis ratio to be 1 for a face-on galaxy, and equal to q0 for a perfectly edge-on galaxy. For an oblate system, we can relate the observed axis ratio to the intrinsic one and the galaxy inclination i0 as (Bottinelli et al. 1983):
Technically, the isodensity surfaces of a double exponential profile are not oblate but have a biconical shape, which means that Eq. D.17 is only an approximation of the real dependence of the observed axis ratio on q0 and inclination. In Sect. 4.1 we fitted 2D profiles of galaxies using a bulge-disk decomposition, assuming that the disk is exponential with zero thickness. Its apparent central surface density is therefore given by Eq. D.14 with i the apparent inclination related to the observed axis ratio through Eq. D.15. If the stellar disk 3D distribution is actually described by a double exponential profile, then its apparent central surface density given by Eq. D.16 must match that of the fitted single exponential profile. Using Eq. D.17 to express the apparent inclination in terms of the real inclination i0 and intrinsic axis ratio q0, we can derive the ratio r0 of the central surface density computed using a double exponential profile against that computed from a single exponential fit as
The ratio of the central surface densities is plotted in Fig. D.2 as a function of the intrinsic axis ratio and real inclination. The central surface density derived in the case of a disk with non-zero thickness is always larger than its infinitely thin disk counterpart, the ratio reaching a maximum
 |
Fig. D.2. Ratio of the central density assuming a double exponential profile with that derived assuming a razor-thin disk exponential fit as a function of the galaxy’s real inclination, i0, and intrinsic axis ratio, q0 = hz/Rd, with Rd the disk scale length. The maximum value is equal to |
at i0 = arctan(1/q0). As is expected, when the disk becomes more and more flattened, the ratio reaches unity. Similarly, when the galaxy is viewed face-on, the central surface densities for both models are equal.
D.5. Correction in the inner parts
The Bovy approximation to the rotation curve of a double exponential profile given by Eq. D.12 has the disadvantage of reaching a null velocity as soon as the correction term on the right-hand side becomes larger than the velocity of the razor-thin disk that appears in the equation, that is, at R > 0. However, the real rotation curve would reach a null velocity at R = 0 if one integrates it numerically. The impact of using Eq. D.12 would be small since we lack the resolution in our MUSE data to model precisely the velocity in the inner parts and because beam-smearing strongly affects the velocity field near the centre. Nevertheless, it can be useful to slightly modify it in order to have a rotation curve that behaves more physically in the inner parts.
To do so, we decided to replace the rotation curve for the double exponential profile near the centre with the tangential line to Bovy approximation, which passes through R = 0. This means that the rotation curve will behave linearly in the inner parts until it reaches the tangential point where Bovy approximation will take over. With R0 the radius at which the corresponding tangential line passes through the point R = 0, the tangent must obey the following equation:
Defining y = R/(2Rd) and y0 = R0/(2Rd), this simplifies to
with the derivative of  given by
given by
where f is defined in Appendix D.2 and α = 4πGRdΥΣRT(0). Furthermore, the derivative of f2 is given by
Thus, combining everything together, the equation one needs to solve to find y0 = R/Rd as a function of the disk thickness q0 is
Equation D.24 was solved numerically for a range of q0 values and was then fitted by a polynomial function of degree five in order to get an analytical approximation of y0 as a function of q0. We found that the best polynomial fit is given by
and we show in Fig. D.3 the relative error on y0 = R/Rd between the analytical approximation given by Eq. D.25 and the numerical solution as a function of the disk thickness.
 |
Fig. D.3. Relative error on R/Rd between the numerical solution of Eq. D.24 and the analytical approximation given by Eq. D.25 as a function of the disk thickness, q0. In the range of disk thicknesses we are interested in, the error does not exceed 2%. |
D.6. Stellar bulge
Galaxy bulges can be described by various 3D distributions such as Plummer or Jaffe profiles (Plummer 1911; Jaffe 1983), but the most interesting one remains the Hernquist profile (Hernquist 1990),
with Mb the total bulge mass and a a scale radius related to the half-mass size r1/2,M through the relation 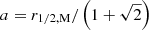 . In the case of a light distribution, the total bulge mass Mb is replaced by the total bulge flux Fb = Mb/Υ. This profile has the advantage of being spherically symmetric, with analytical forms of its gravitational potential and circular velocity, while having a line of sight projected surface density close to a de Vaucouleurs profile, except towards the inner parts. Therefore, describing the bulge 3D mass distribution as an Hernquist profile seems to be the most relevant choice. The circular velocity can be written as
. In the case of a light distribution, the total bulge mass Mb is replaced by the total bulge flux Fb = Mb/Υ. This profile has the advantage of being spherically symmetric, with analytical forms of its gravitational potential and circular velocity, while having a line of sight projected surface density close to a de Vaucouleurs profile, except towards the inner parts. Therefore, describing the bulge 3D mass distribution as an Hernquist profile seems to be the most relevant choice. The circular velocity can be written as
where  is the maximum circular velocity reached at a radius r = a.
is the maximum circular velocity reached at a radius r = a.
D.7. Hernquist - de Vaucouleurs mapping
To compute the rotation curve of the bulge component, one needs to map the de Vaucouleurs parameters (Σeff,b,Reff,b) from GALFIT with the parameters (Fb,a) of the Hernquist model whose line of sight projected surface brightness matches best that of the Sérsic model. We generated 2 500 line of sight projected Hernquist models on a log10a − log10Fb grid in the ranges − 1 ≤ log10a/kpc ≤ 1 and − 4 ≤ log10Fb/10−20 erg s−1 Å−1 ≤ 6, and for each model, a de Vaucouleurs profile was fitted by minimising the root mean square error using the Levenberg-Marquardt algorithm. The bounds for both parameters were chosen based on previous tests that showed that these values correspond to the typical sizes and surface brightnesses we have in our HST data. After inspection, it seems that the Hernquist parameters can be mapped to the Sérsic ones through the two following scaling relations:
The error on these two scaling relations is shown in Fig. D.4. While not being perfect, for typical bulge sizes around 2 kpc the error is around 5%. We find the following best-fit scaling parameters: αa = −0.454, βa = 0.725, αF = 1.194 and βF = 1.75. Examples of Sérsic profiles and their associated projected Hernquist profiles using Eq. D.28 and D.29 are shown in Fig. D.5. The two profiles start diverging towards large radii where the Sérsic profile drops more rapidly than the Hernquist one.
 |
Fig. D.4. Log difference of the best-fit scaling relations from Eqs. D.28 and D.29 with the derived parameters θ∈ } a,Fb/Σeff,b{ as a function of the bulge effective radius. The variation in the Hernquist parameters a and Fb with Reff,b was derived by generating a grid of Hernquist models, projecting each model along the line of sight, and fitting them with de Vaucouleurs profiles. In the range of bulge sizes we are interested in, the error on the parameters is around 5%. |
 |
Fig. D.5. Examples of de Vaucouleurs profiles (dashed lines) and their corresponding sky projected Hernquist profiles (continuous lines) using the scaling relations in Eqs. D.28 and D.29. From top to bottom, the Sérsic parameters are (Σeff, Reff)=(10−3, 0.5) (orange), (10−3, 6) (blue), (0.1, 0.5) (red), and (0.1, 6) (grey). Because the deviation of the projected Hernquist profile to the Sérsic one occurs mainly at large distances, where the surface brightness quickly drops, the overall fluxes are actually in quite good agreement. |
By construction, the Hernquist amplitude parameter Fb should be equal to the total de Vaucouleurs flux, but because the total flux is proportional to 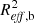 while Fb is proportional to
while Fb is proportional to  , in practice, this means that our parametrisation, while recovering the shape of a de Vaucouleurs profile for a broad part of the radial range, will underestimate or overestimate the real flux contribution, and therefore the maximum circular velocity of the bulge component. Using Eq. C.1, D.29 and D.27, we can derive the error on Vb, max as a function of the de Vaucouleurs parameters
, in practice, this means that our parametrisation, while recovering the shape of a de Vaucouleurs profile for a broad part of the radial range, will underestimate or overestimate the real flux contribution, and therefore the maximum circular velocity of the bulge component. Using Eq. C.1, D.29 and D.27, we can derive the error on Vb, max as a function of the de Vaucouleurs parameters
where ΔVb, max = Vb, max(Fb)−Vb, max(Ftot), with Vb, max(Fb) and Vb, max(Ftot) the maximum circular velocities from Eq. D.27 using the Hernquist amplitude parameter and the total de Vaucouleurs flux, respectively. Therefore, our parametrisation overestimates the bulge circular velocity for bulge sizes Reff,b ≲ 3.6 kpc, and underestimates it beyond, with a maximum relative difference of 50% when Reff,b → ∞. Nevertheless, these differences need to be weighted out by two facts
-
(i)
as can be seen in Fig. A.2, bulges mainly have radii below 1.5 − 2 kpc where the difference is mostly negligible given the uncertainties on the other parameters and the assumption of a constant mass to light ratio,
-
(ii)
very small bulge sizes where we may expect the largest differences to arise are in practice associated with really weak bulge contribution, that is, Σeff,b ∼ 0, and therefore to a negligible rotation.
D.8. Dark matter halo
Apart from the baryonic disk and bulge components, we also model the galaxies DM halo with an NFW profile (Navarro et al. 1995),
where rs = r200/c is the halo scale radius, with r200 the virial radius of the halo where the mean overdensity is equal to 200 and c the halo concentration,  the Universe closure density and δc the halo characteristic overdensity (Navarro et al. 1996). The associated circular velocity is given by
the Universe closure density and δc the halo characteristic overdensity (Navarro et al. 1996). The associated circular velocity is given by
where Vh, max is the maximum rotation velocity reached at a radius r ≈ 2.163rs.
Appendix E: Sky projection of a double exponential profile
We consider the double exponential disk model of the form ρd(r) = ρd(R,z) with R the radius in the plane of the disk and z the direction orthogonal to the disk. We define three new coordinates, (x′,y′,z′), such that (x′,y′,0) corresponds to the plane of the sky (see Fig. E.1). Furthermore, the axis defined by x = x′ corresponds to the intersection between the plane of the disk and the plane of the sky. Computing the surface density of the inclined 3D distribution at position (x′,y′) on the plane of the sky amounts to solving the following integral:
 |
Fig. E.1. Geometry of the line of sight integration problem. For each point (x′,y′) in the plane of the sky, the 3D density disk distribution ρd(x, y, z) must be integrated along a line of constant R′ = (x′2 + y′2)1/2. The angle θ is oriented such that it is positive for z′> 0 and negative otherwise. |
Therefore, one must write R and z as functions of x′, y′ and z′. To do so, we define r, the distance of a point in the (y′,z′) plane, and θ, the angle between the r axis and y′, where θ is an oriented angle that varies between −π/2 and π/2. We have
Since the integral is computed along a line of constant y′, we can plug Eq. E.2 into Eq. E.3 after developing the cosine and sine terms to get
Using the expression for the double exponential profile (see Eqs. D.7 and D.10) we get
We can simplify this integral by making the change of variable v = y/Rd and by defining the following parameters:
with q0 = hz/Rd the intrinsic axis ratio of the galaxy. The integral becomes
The original problem of solving Eq. E.1 for the double exponential profile required 6 free parameters, namely x′, y′, Σd(0, 0), Rd, hz and i, with Σd(0, 0) only acting as an amplitude parameter, but Eq. E.10 reduces the dimensionality of the problem to 3 free parameters only to compute the integral. In the general case, there is no straightforward analytical solution or numerical approximation to the integral above, though a solution can be derived along the y′ axis when x = 0:
Appendix F: MAGIC catalogue
Column description of the MAGIC catalogue, which contains morpho-kinematics and physical parameters for the MS sample of 447 galaxies.
Appendix G: Example of morpho-kinematics maps
We show below an example of a morpho-kinematics map. The maps for all the galaxies in the MS sample are sorted according to their (RA 2000, Dec 2000) coordinates and can be found online.
 |
Fig. G.1. Morpho-kinematics map for galaxy 121-CGR61. From top to bottom and left to right: HST-ACS image, GALFIT model, HST residuals, CAMEL velocity field, MOCKING velocity field model, velocity field residuals, CAMEL velocity dispersion map, MOCKING beam smearing model (including spectral resolution broadening), and beam smearing and LSF corrected velocity dispersion map. The morpho-kinematics centre and the morphological PA are shown in the HST image and the CAMEL maps as a green cross and a green line whose length corresponds to R22, respectively. The PSF FWHM is indicated as the grey disk in the velocity field. The [OII] surface brightness distribution is overlaid on top of the HST and MUSE [OII] flux maps, with contours at levels Σ[O II] = 2.5,5,10,20,40 and 80 × 10−18 erg s−1 cm−2 arcsec−2. |
All Tables
Comparison of fit parameters for the scaling relations with various selection criteria.
Column description of the MAGIC catalogue, which contains morpho-kinematics and physical parameters for the MS sample of 447 galaxies.
All Figures
 |
Fig. 1. Redshift distribution for the three initial sub-samples defined in Sect. 3.2. The samples of field galaxies (grey area) and galaxies in small structures (dashed blue line) have relatively flat distributions. The peak of the distribution for galaxies in large structures (red line) is located at redshift z ∼ 0.7 and is driven by the largest structures (40 ≲ N ≲ 100) found in the COSMOS area of the MAGIC sample. |
| In the text | |
 |
Fig. 2. SFR-M⋆ diagram for galaxies from the kinematics sample (see Sect. 6.1). Galaxies are separated between the field (black points), small structures (blue triangles), and large structures (red circles). The typical stellar mass and SFR error is shown on the bottom right. The SFR was normalised to redshift z0 = 0.7. The SFR and mass distributions are shown as histograms to the top and right, respectively, with the median values for each sample represented as lines of similar colours. |
| In the text | |
 |
Fig. 3. Bulge-to-total flux ratio distribution computed at one effective radius for galaxies in the morphological sample located in various environments. The legend is similar to that of Fig. 1. The vertical lines correspond to the median B/T values for each sample. The grey area in the background indicates which galaxies were selected in the kinematics sample (see Sect. 5.1). |
| In the text | |
 |
Fig. 4. Impact of stellar mass correction as a function of the SED-based stellar mass for galaxies from the morphological sample. Overall, the correction lowers the stellar mass, reducing it by as much as a factor of 1.5. We see that the smaller the disk radius, Reff,d (or equivalently R22), the larger the stellar mass reduction, consistent with the fact that the SED-based stellar mass computed in an aperture of 3″ usually overestimates the real value, though in practice this effect can be compensated for by sky projection and PSF effects. |
| In the text | |
 |
Fig. 5. Observed axis ratio, q, as a function of redshift for galaxies from the morphological sample (black points) after removing bulge-dominated galaxies and those with small disk sizes. The median values for the six most edge-on galaxies in redshift bins of width Δz = 0.15 are shown as red squares. The red line represents the thickness prescription that was applied. Independently of mass, galaxies tend to have thinner disks at larger redshifts, which may be due to the fact that we probe younger stellar populations at higher redshifts when observing in a single band. |
| In the text | |
 |
Fig. 6. Distribution of disk inclination for galaxies from the morphological sample, after removing bulge-dominated galaxies and those with small disk sizes. We show the distribution before correcting for the finite thickness of the disk (black line) and after the correction (red hatched area). The dashed orange line represents the binned theoretical distribution expected for randomly oriented disk galaxies. The correction tends to increase the fraction of edge-on galaxies. While being closer to the theoretical distribution at large inclinations, the corrected inclinations still do not match the distribution of randomly inclined galaxies. |
| In the text | |
 |
Fig. 7. Rotation curves for the flat (green line) and mass models (orange dashed) of galaxy 104-CGR79 at redshift z = 0.53. The components are the bulge (red), the thin disk (blue), and the DM halo (black). We also show the observed de-projected (but beam-smeared) rotation curves extracted along the major axis from the observed velocity field map (black crosses), from the best-fit velocity field flat model (green circles), and from the best-fit velocity field mass model (orange triangles). The largest difference between the flat and mass models is found in the inner parts, where the beam smearing is the strongest. The total dynamical mass differs slightly between models, with the flat one being 4% higher than the mass model one. |
| In the text | |
 |
Fig. 8. Examples of morpho-kinematics modelling for galaxies with IDs 132-CGR32 and 104-CGR79 (both in large structures) and 77-CGR30 and 86-CGR114 (both in the field). In each panel, from top to bottom and left to right: (a) HST-ACS image, (b) GALFIT model, (c) HST residuals, (d) CAMEL velocity field, (e) MOCKING velocity field model, (f) velocity field residuals, (g) CAMEL velocity dispersion map, (h) MOCKING beam smearing model, including spectral resolution broadening, and (i) beam smearing and LSF corrected velocity dispersion map. The morpho-kinematics centre and the morphological PA are respectively shown in the HST image and the CAMEL maps as a green cross and a green line, whose length corresponds to R22. The PSF FWHM is indicated as the grey disk in the velocity field. The [O II] surface brightness distribution is overlaid on top of the HST and MUSE [O II] flux maps, with contours at levels Σ[O II] = 2.5,5,10,20,40, and 80 × 10−18 erg s−1 cm−2 arcsec−2. |
| In the text | |
 |
Fig. 9. S/N-disk effective radius-B/D selection plot for galaxies from the kinematics sample. The disk size selection criterion is represented as the vertical line. The S/N selection criterion depends on the FWHM, which varies with redshift and MUSE field. As an example, we show the S/N limit used for a typical FWHM of 0.65″. Points are colour-coded according to their bulge-to-disk ratio computed at one effective radius. The grey areas give an idea of the galaxies eliminated by the size and S/N selection criteria. We also show the ten galaxies eliminated by selection criterion v (orange crosses) and the three we decided to keep (orange circles). |
| In the text | |
 |
Fig. 10. Impact of the different selection criteria from Sect. 6.1 applied to the size-mass relation (top left), the TFR (bottom left), and the MS relation (bottom right). Black circles represent galaxies that remain when all the selection criteria are applied. Given that some selections remove similar galaxies, we show those removed by the S/N (orange squares), size (blue downward-pointing triangles), and redshift criteria (red triangles), in this order. Additionally, we also show the galaxies removed by the inclination selection (green diamonds) in the TFR before the redshift selection was applied. |
| In the text | |
 |
Fig. 11. Size-mass relation for galaxies from the MS sample with additional mass and redshift cuts applied (vi and vii). Symbols and colours are similar to those in Fig. 2, and orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit lines are shown when using a richness threshold N = 10 (full lines) and N = 20 (dashed lines). The dashed black line is not visible since field galaxies have the same best-fit line for N = 10 and N = 20. We do not show galaxies in the small structure sub-sample since too few galaxies remain after selection criteria (vi) and (vii) are applied. We also provide in the top left the slope and best-fit zero point for each sub-sample (see Eq. (12) with y = Rd and x = M⋆). The typical uncertainty on stellar mass and disk size is shown in the bottom right as a grey error bar. After controlling for differences in mass and redshift, we find a 1σ significant difference of 0.03 dex between sub-samples with N = 10, and a 2σ significant difference of 0.06 dex with N = 20. |
| In the text | |
 |
Fig. 12. SFR-stellar mass relation for galaxies from the MS sample with additional mass and redshift cuts applied (vi and vii). Symbols and colours are similar to those in Fig. 2, and orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit lines are shown when using a richness threshold N = 10 (full lines) and N = 20 (dashed lines). We do not show galaxies in the small structure sub-sample since too few galaxies remain after selection criteria (vi) and (vii) are applied. The SFR is normalised to redshift z0 = 0.7 (see Sect. 3.3). We also provide the slope and best-fit zero point for each sub-sample in the top left (see Eq. (12) with y = SFR and x = M⋆). The typical uncertainty on stellar mass and SFR is shown in the bottom right as a grey error bar. Even after controlling for differences in mass and redshift, we find a 2σ significant difference of 0.10 dex between sub-samples with N = 10, and a 3σ significant difference of 0.15 dex with N = 20. |
| In the text | |
 |
Fig. 13. Stellar mass TFR at R22 for galaxies from the TFR sample with mass and redshift cuts applied (vi and vii). The top panel shows the TFR using the velocity computed from the mass models, and the bottom shows the TFR using the velocity from a flat model. Galaxies are split between field and small structure (black points) and large structure (red circles) sub-samples using a richness threshold of N = 10. Orange stars represent galaxies identified as outliers from the fit done with LTSFIT. As an indication, we also show as semi-transparent symbols galaxies removed by the mass and redshift cuts. Best-fit linear relations for both sub-samples are shown as full lines. We provide in the bottom part of each panel the slope and best-fit zero points (see Eq. (12) with y = V22 and x = M⋆,corr). The typical uncertainty on stellar mass and velocity is shown as a grey error bar. After controlling for differences in mass and redshift, we do not find any impact of the environment on the zero point of either TFR. |
| In the text | |
 |
Fig. 14. Evolution of the median stellar and baryon fractions for galaxies from the TFR sample in the field (black points) and in large structures (red circles) as a function of stellar mass in mass bins of 1 dex. Light grey error bars correspond to the 16th and 84th percentiles of the baryon fraction distributions. The typical uncertainty on stellar mass and baryon fraction is shown as a dark grey error bar on the bottom right. Because we removed galaxies whose mass models have large uncertainties (selection criteria iv and v), the fractions we measure are probably slightly underestimated. |
| In the text | |
 |
Fig. A.1. Comparison of the circular velocity V22 = V(R22) using MOCKING between MULTINEST and MPFIT for galaxies from the MS sample. The rotation curve used was a flat model, and we removed galaxies whose circular velocity could not be reliably constrained (R22 falls outside the range where there is sufficient S/N in the MUSE data cube to derive the kinematics). Red points correspond to galaxies visually classified as having no apparent velocity field in their kinematics maps, and dashed red lines correspond to a 50% difference between the two methods. The typical uncertainty is shown in the bottom-right part of the plot. Overall, values are consistent within their error bars. |
| In the text | |
 |
Fig. A.2. Distribution of effective radii for galaxies in the morphological sample. In grey (filled) we show the total size, in red (hatched) the bulge size, and in blue (hatched) the disk size. Disks are mostly found between roughly 1 kpc and 6 kpc, with very few galaxies with disk sizes beyond 10 kpc. The lack of disks below 1 kpc is due to the size selection criterion from Sect. 6.1. On the other hand, the majority of bulges are found below 2 kpc. The total size of galaxies is mainly driven by the disk component. |
| In the text | |
 |
Fig. A.3. SFR-stellar mass relation for galaxies from the MS sample, colour-coded as a function of redshift. Despite the applied normalisation to redshift z0 = 0.7, we still see a dichotomy. High redshift galaxies tend to align along lines with the largest specific star formation rate (sSFR), while low redshift galaxies tend to align along lines with the lowest sSFR because of the survey design. |
| In the text | |
 |
Fig. B.1. Size-mass relation with and without applying the mass selection criterion (vi) on galaxies from the MS sample. The data points and best-fit lines are similar to Fig. 11. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the right panel. The typical uncertainty on stellar mass and disk size is shown on both panels as a grey error bar. |
| In the text | |
 |
Fig. B.2. SFR-mass relation with and without applying the mass selection criterion (vi) on galaxies from the kinematics sample. The data points and best-fit lines are similar to Fig. 12. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the right panel. The typical uncertainty on stellar mass and SFR is shown on both panels as a grey error bar. |
| In the text | |
 |
Fig. B.3. TFR with and without applying the mass selection criterion (vi) on galaxies from the TFR sample. The data points and best-fit lines are similar to Fig. 13. The first row shows the TFR using the velocity derived from the best-fit mass models, and the second row the TFR using the flat model. As an indication, we also show as semi-transparent symbols galaxies removed by the mass cut in the rightmost panels. The typical uncertainty on stellar mass and velocity is shown on each panel as a grey error bar. |
| In the text | |
 |
Fig. B.4. Impact of selection criteria on the main parameters distributions for galaxies from the kinematics sample. Each row represents a different selection. The black full line corresponds to the field galaxy sub-sample, the blue dashed line to the small structures and the red thick line to the large structures (using a threshold of N = 10 to separate between structures). We also show the median values for each sub-sample as vertical lines. We do not show the small structure sub-sample in the last two rows since there remain too few galaxies. |
| In the text | |
 |
Fig. C.1. Mean B/T for galaxies in the morphological sample computed at various radii in units of Reff. The areas correspond to the 1σ (dark grey) and 2σ (light grey) dispersions. The bulge component dominates the central parts of the galaxies whereas the disk takes over completely after roughly one effective radius. Even as far as 10Reff, we find a nearly constant non-zero B/T ≈ 0.2 indicative of a non-negligible bulge contribution to the overall flux budget. |
| In the text | |
 |
Fig. D.1. Impact of the thickness on the shape of the rotation curve for a thin disk. The finite thickness only impacts the inner parts and changes both the amplitude and the radius where the maximum is reached. |
| In the text | |
 |
Fig. D.2. Ratio of the central density assuming a double exponential profile with that derived assuming a razor-thin disk exponential fit as a function of the galaxy’s real inclination, i0, and intrinsic axis ratio, q0 = hz/Rd, with Rd the disk scale length. The maximum value is equal to |
| In the text | |
 |
Fig. D.3. Relative error on R/Rd between the numerical solution of Eq. D.24 and the analytical approximation given by Eq. D.25 as a function of the disk thickness, q0. In the range of disk thicknesses we are interested in, the error does not exceed 2%. |
| In the text | |
 |
Fig. D.4. Log difference of the best-fit scaling relations from Eqs. D.28 and D.29 with the derived parameters θ∈ } a,Fb/Σeff,b{ as a function of the bulge effective radius. The variation in the Hernquist parameters a and Fb with Reff,b was derived by generating a grid of Hernquist models, projecting each model along the line of sight, and fitting them with de Vaucouleurs profiles. In the range of bulge sizes we are interested in, the error on the parameters is around 5%. |
| In the text | |
 |
Fig. D.5. Examples of de Vaucouleurs profiles (dashed lines) and their corresponding sky projected Hernquist profiles (continuous lines) using the scaling relations in Eqs. D.28 and D.29. From top to bottom, the Sérsic parameters are (Σeff, Reff)=(10−3, 0.5) (orange), (10−3, 6) (blue), (0.1, 0.5) (red), and (0.1, 6) (grey). Because the deviation of the projected Hernquist profile to the Sérsic one occurs mainly at large distances, where the surface brightness quickly drops, the overall fluxes are actually in quite good agreement. |
| In the text | |
 |
Fig. E.1. Geometry of the line of sight integration problem. For each point (x′,y′) in the plane of the sky, the 3D density disk distribution ρd(x, y, z) must be integrated along a line of constant R′ = (x′2 + y′2)1/2. The angle θ is oriented such that it is positive for z′> 0 and negative otherwise. |
| In the text | |
 |
Fig. G.1. Morpho-kinematics map for galaxy 121-CGR61. From top to bottom and left to right: HST-ACS image, GALFIT model, HST residuals, CAMEL velocity field, MOCKING velocity field model, velocity field residuals, CAMEL velocity dispersion map, MOCKING beam smearing model (including spectral resolution broadening), and beam smearing and LSF corrected velocity dispersion map. The morpho-kinematics centre and the morphological PA are shown in the HST image and the CAMEL maps as a green cross and a green line whose length corresponds to R22, respectively. The PSF FWHM is indicated as the grey disk in the velocity field. The [OII] surface brightness distribution is overlaid on top of the HST and MUSE [OII] flux maps, with contours at levels Σ[O II] = 2.5,5,10,20,40 and 80 × 10−18 erg s−1 cm−2 arcsec−2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![$$ \begin{aligned} \mathrm{{SFR}}~[{{\text{M}_{\odot }\,\mathrm {yr}^{-1}}}] = (1.4 \pm 0.4) \times 10^{-41}\,L_{\rm {[{\text{O}}{\small {{\text{ II}}}}]}}\,[\mathrm{{erg\,s^{-1}}}], \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq18.gif)
![$$ \begin{aligned} F_{\rm {[{\text{O}}{\small {{\text{ II}}}}], corr}} = F_{\rm {[{\text{O}}{\small {{\text{ II}}}}]}} \times 10^{0.4 \left( A_{\mathrm{{H}}\alpha } + A_{\rm {[{\text{O}}{\small {{\text{ II}}}}], MW}} \right)}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq20.gif)

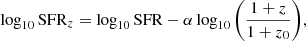
![$$ \begin{aligned}&10^{-\mathrm{{mag_d}} /2.5} \left[ \gamma \left(2, b_1 \frac{R_{\mathrm{eff}}}{R_{\mathrm{eff}, \mathrm {d}}} \right) - 0.5 \right] \nonumber \\&\quad + 10^{-\mathrm{{mag_b}} /2.5} \left[ \gamma \left(8, b_4 \left(\frac{R_{\mathrm{eff}}}{R_{\mathrm{eff}, \mathrm {b}}} \right)^{1/4} \right) / \Gamma (8) - 0.5 \right] = 0 , \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq23.gif)




![$$ \begin{aligned} ({\mathrm{S/N}})_{\rm {tot}} = \sum _{x, { y}} F_{[{\text{O}}{\small {{\text{ II}}}}]} (x, { y}) \left. \sqrt{\sum _{x, { y}} \left[ \frac{F_{[{\text{O}}{\small {{\text{ II}}}}]} (x, { y})}{\mathrm{{S/N}} (x,{ y})} \right]^2}\right.\!, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq29.gif)

![$$ \begin{aligned} \log _{10} \Sigma _{\rm {M, d}} (0)\,[{{\mathrm{M}_{\odot }\,\mathrm{kpc}}}^{-2}] \approx 0.32 \log _{10} M_{\star , \mathrm {corr}}~[{\mathrm{M}}_{\odot }] + 5.65 - 2\beta _{\rm {sm}}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq82.gif)

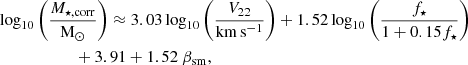
![$$ \begin{aligned} \Delta \log _{10} M_{\star , \mathrm {corr}}[{\mathrm{M}_{\odot }}] = 1.52 \left[ \Delta \log _{10} \left( \frac{f_{\star }}{1+0.15 f_{\star }} \right) + \Delta \beta _{\rm {sm}} \right]\!, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq87.gif)
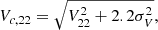
![$$ \begin{aligned}&\log _{10} M_{\rm {g}}~[{\mathrm{M}}_{\odot }] \approx 8.053 + 0.571 \log _{10} R_{\rm {d}}\,[\mathrm{{kpc}}] \nonumber \\&\qquad \qquad \qquad + 0.714 \log _{10} \mathrm{{SFR}}~[{\mathrm{M}}_{\odot }~\mathrm{{yr}}^{-1}], \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq89.gif)



![$$ \begin{aligned}&F_{\rm {tot, d}} \left[ \gamma \left( 2, b_1 \frac{R_{\textit{eff}}}{R_{\textit{eff}, \mathrm {d}}} \right) - 0.5 \right] + \nonumber \\&\frac{F_{\rm {tot, b}}}{\Gamma (8)} \left[ \gamma \left(8, b_4 \left( \frac{R_{\textit{eff}}}{R_{\textit{eff}, \mathrm {b}}} \right)^{1/4} \right) - \Gamma (8) / 2 \right] = 0. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq93.gif)

![$$ \begin{aligned} f(x)&= 10^{-\mathrm{{mag_d}} /2.5} \left[ \gamma \left(2, b_1 \frac{x}{R_{\textit{eff} \mathrm {d}}} \right) - 0.5 \right] + \nonumber \\&10^{-\mathrm{{mag_b}} /2.5} \left[ \gamma \left(8, b_4 \left(\frac{x}{R_{\textit{eff}, \mathrm {b}}} \right)^{1/4} \right) / \Gamma (8) - 0.5 \right]. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq95.gif)






![$$ \begin{aligned} \Sigma _{\rm {RT}} (R)&= \Sigma _{\rm {RT}} (0)~e^{- b_1 [ R/R_{\textit{eff}, \mathrm {d}} ]}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq102.gif)



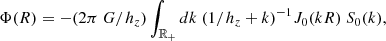











![$$ \begin{aligned} \frac{dV^2_{\rm {d}}}{dy} (y_0)&= V^2_{\rm {d}} (y_0) / y_0 + \nonumber \\&\alpha y_0 \left[ f^2(y_0) + y_0 \frac{df^2}{dy} (y_0) + 2 q_0 e^{-2y_0} \right], \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq120.gif)

![$$ \begin{aligned} y_0^2 \left[ I_1 (y_0) K_0 (y_0) - I_0 (y_0) K_1 (y_0) \right] +&y_0 I_1 (y_0) K_1 (y_0) + \nonumber \\&q_0 \left(y_0 + 0.5 \right) e^{-2 y_0} = 0. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq122.gif)



![$$ \begin{aligned} \log _{10} a \,[\mathrm {kpc}]&= \alpha _a + \beta _a \log _{10} R_{\textit{eff}, \mathrm {b}} [\mathrm {kpc}] \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq128.gif)
![$$ \begin{aligned} \log _{10} F_{\rm {b}} / \Sigma _{\textit{eff}, \mathrm {b}} \,[\mathrm {cm}^2]&= \alpha _F + \beta _F \log _{10} R_{\textit{eff}, \mathrm {b}} [\mathrm {kpc}]. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq129.gif)
![$$ \begin{aligned} \Delta V_{\rm {b, max}} / V_{\rm {b, max}} (F_{\rm {tot}}) = 0.5 \left[ 1.174 \left(R_{\textit{eff}, \mathrm {b}} / \mathrm {kpc} \right)^{-0.125} - 1 \right], \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq132.gif)

![$$ \begin{aligned} V_{\rm {h}}(r) = \frac{V_{\rm {h, max}}}{0.46499} \left[ \frac{\ln \left(1 + r/r_{\rm {s}} \right)}{r/r_{\rm {s}}} - \frac{1}{1 + r/r_{\rm {s}}} \right]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43110-22/aa43110-22-eq135.gif)











